Counting and Enumerating the Number of Divisors of a Natural Number by James Pate Williams, Jr.

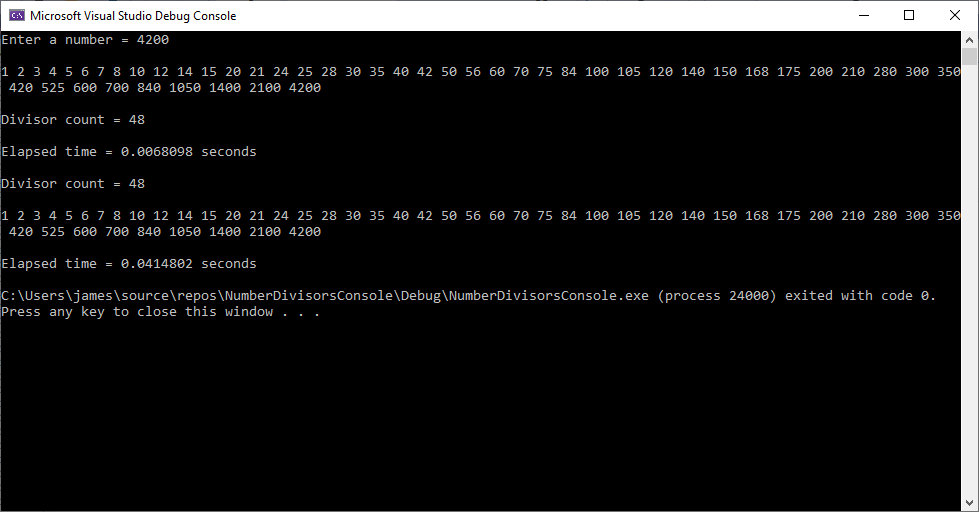
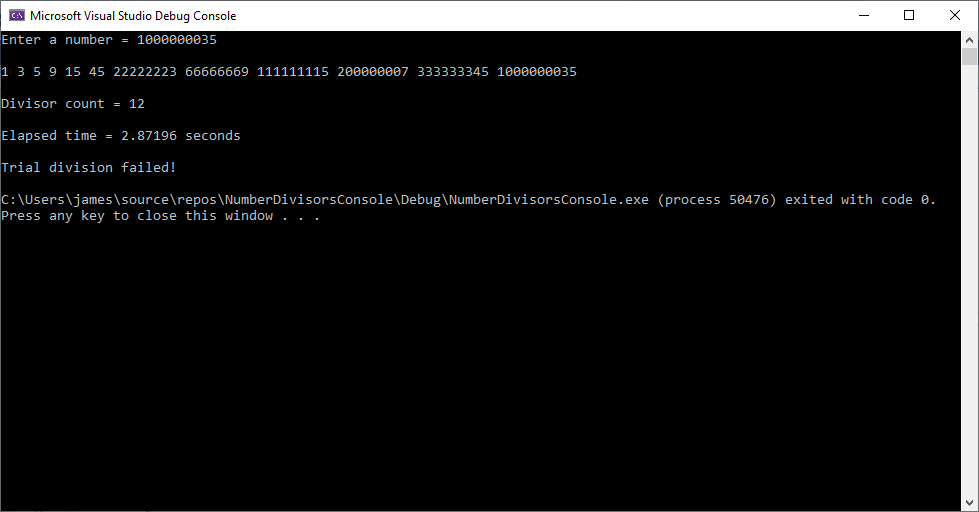
A simple number theoretic problem is to count and enumerate the number of divisors of a natural number which is the set { 1, 2, 3, … }. An Order(n) method is to find all numbers between 1 and n such that the number divides n. If you have the prime factorization of n then the number of divisors is the product of the prime factorization (exponents + 1). For example the divisors of 100 are:

1 2 4 5 10 20 25 50 100

The prime factorization of 100 = 2^2 * 5 ^ 2. So the number of divisors is (2 + 1) * (2 + 1) = 9.

Below is a C++ implementation of an algorithm to enumerate and count the number of divisors of a natural number and count the divisors by using the factorization found by trial division.

#include <algorithm>
#include <chrono>
#include <iostream>
#include <vector>
using namespace std;

const int B0 = 10000000;

bool sieve[B0 + 1];
vector<int> prime, divisors, expon, primes, primesSquares;

void Sieve()
{
	// Sieve of Eratosthenes
	// find all prime numbers
	// less than or equal B0

	int c = 3, i, inc;

	sieve[2] = true;

	for (i = 3; i <= B0; i++)
		if (i % 2 == 1)
			sieve[i] = true;

	do
	{
		i = c * c;
		inc = c + c;

		while (i <= B0)
		{
			sieve[i] = false;

			i += inc;
		}

		c += 2;

		while (!sieve[c])
			c++;

	} while (c * c <= B0);

	for (i = 2; i <= B0; i++)
	{
		if (sieve[i])
		{
			primes.push_back(i);
			primesSquares.push_back(i * i);
		}
	}
}

bool TrialDivision(int number)
{
	int bound = B0; // (int)sqrt(number);

	for (int i = 0; i < (int)primes.size(); i++)
	{
		int p = primes[i];

		if (p <= bound)
		{
			if (number % p == 0)
			{
				int e = 0;

				while (number % p == 0)
				{
					e++;
					number /= p;
				}

				prime.push_back(p);
				expon.push_back(e);
			}

			if (number == 1)
				return true;
		}
	}

	return false;
}

void GetDivisors(int n, int count)
{
	divisors.push_back(1);

	for (int i = 0; i < (int)prime.size(); i++)
	{
		int p = prime[i];

		for (int j = 1; j <= (int)expon[i]; j++)
		{
			int q = (int)pow(p, j);

			divisors.push_back(q);
		}
	}

	bool done = false;
	int limit;

	do
	{
		limit = (int)divisors.size();

		for (int i = 1; i < limit - 1; i++)
		{
			int di = divisors[i];

			for (int j = i + 1; !done && j < limit; j++)
			{
				int dj = divisors[j], product = di * dj;
				vector<int>::iterator it =
					find(divisors.begin(), divisors.end(), product);

				if (it == divisors.end())
				{
					if (divisors.size() < count &&
						product <= n && n % product == 0)
						divisors.push_back(product);

					else if (divisors.size() == count)
						done = true;
				}
			}
		}
	} while (!done);

	std::sort(divisors.begin(), divisors.end());
}

int main()
{
	int count = 0, number;

	std::cout << "Enter a number = ";
	cin >> number;
	std::cout << endl;

	auto start = chrono::high_resolution_clock::now();

	for (int i = 1; i <= number; i++)
	{
		if (number % i == 0)
		{
			cout << i << ' ';
			count++;
		}
	}

	auto finish = chrono::high_resolution_clock::now();

	std::cout << endl << endl;
	std::cout << "Divisor count = " << count << endl << endl;

	chrono::duration<double> elapsed = finish - start;

	std::cout << "Elapsed time = " << elapsed.count()
		<< " seconds" << endl << endl;

	start = chrono::high_resolution_clock::now();

	Sieve();

	if (!TrialDivision(number))
	{
		cout << "Trial division failed!" << endl;
		return 0;
	}

	count = 1;

	for (int i = 0; i < (int)expon.size(); i++)
		count *= expon[i] + 1;

	finish = chrono::high_resolution_clock::now();

	std::cout << "Divisor count = " << count << endl << endl;

	GetDivisors(number, count);

	for (int i = 0; i < (int)divisors.size(); i++)
		std::cout << divisors[i] << " ";

	std::cout << endl << endl;

	elapsed = finish - start;

	std::cout << "Elapsed time = " << elapsed.count()
		<< " seconds" << endl;
}