Rexx Emulation by James Pate Williams, Jr.

Rexx was a popular computer programming language on IBM main frame computers. I found an interesting website: https://en.wikipedia.org/wiki/Rexx#NUMERIC\

I use a very slowly converging infinite series and Fourier series to compute Pi.

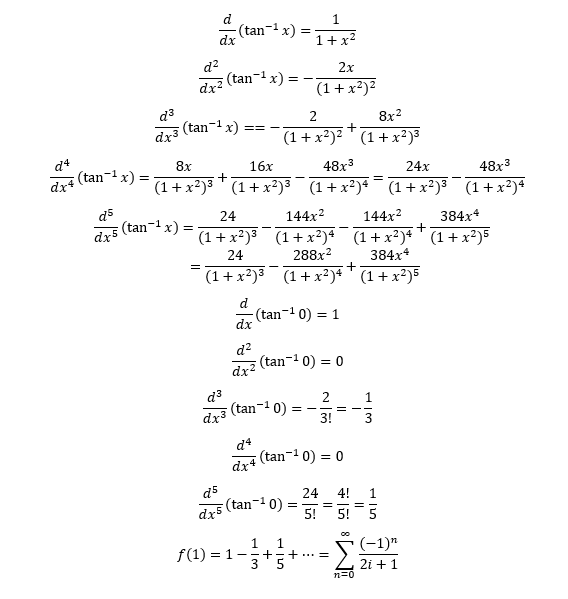
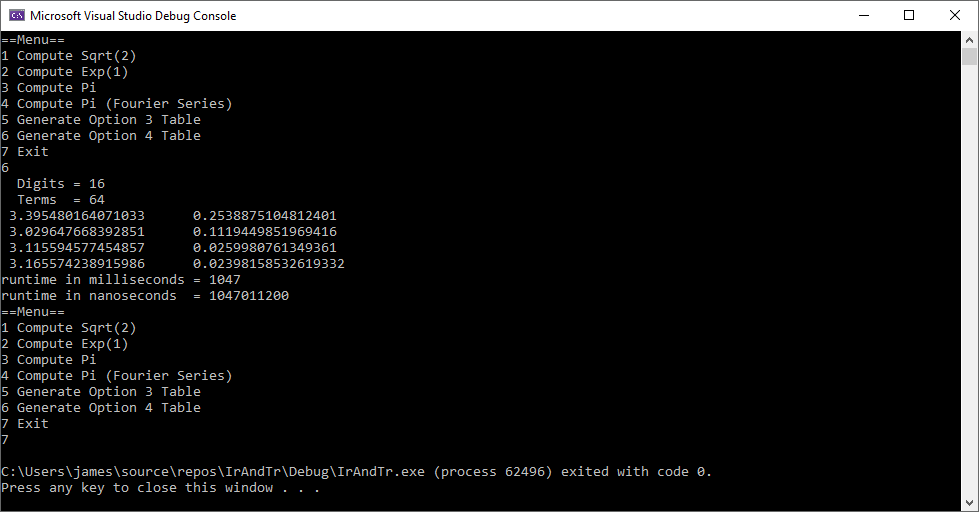
// https://en.wikipedia.org/wiki/Rexx#NUMERIC\
// Translated from Rexx code
// by James Pate Williams, Jr.
// Added a lot of functionality
// Copyrighted February 7 - 10, 2023

#include "FourierSeries.h" 
#include <stdlib.h>
#include <iomanip>
#include <iostream>
#include <chrono>
using namespace std;
typedef chrono::high_resolution_clock Clock;

void Option3(int digits, int N)
{
    long double i = 0;
    long double sgn = 1;
    long double sum = 0;
    long double pi0 = Pi;
    long double pi1 = 0.0;

    while (i <= N)
    {
        sum += sgn / (2.0 * i + 1);
        sgn *= -1;
        i = i + 1.0;
    }

    pi1 = 4.0 * sum;
    cout << setw(static_cast<std::streamsize>((int)digits) + 2);
    cout << setprecision(digits) << pi1 << '\t';
    cout << setprecision(digits) << (fabsl(pi0 - pi1)) << endl;
}

void Option4(int digits, int N)
{
    long double* a = new long double[N + 1];
    long double* b = new long double[N + 1];
    memset(a, 0, (N + 1) * sizeof(long double));
    memset(b, 0, (N + 1) * sizeof(long double));
    FourierSeries::CreateCosSeries(N, a);
    FourierSeries::CreateSinSeries(N, b);
    long double pi = 4.0 * FourierSeries::Series(N, 1.0, a, b);
    cout << setw(static_cast<std::streamsize>((int)digits) + 2);
    cout << setprecision(digits) << pi << '\t';
    cout << setprecision(digits) << (fabsl(pi - Pi)) << endl;
    delete[] a;
    delete[] b;
}

int main()
{
    int choice, digits, N = 0, N1 = 0;

    while (1)
    {
        cout << "==Menu==" << endl;
        cout << "1 Compute Sqrt(2)" << endl;
        cout << "2 Compute Exp(1)" << endl;
        cout << "3 Compute Pi" << endl;
        cout << "4 Compute Pi (Fourier Series)" << endl;
        cout << "5 Generate Option 3 Table" << endl;
        cout << "6 Generate Option 4 Table" << endl;
        cout << "7 Exit" << endl;
        cin >> choice;
        if (choice == 7)
            break;
        cout << "  Digits = ";
        cin >> digits;
        if (choice >= 3)
        {
            cout << "  Terms  = ";
            cin >> N;
            N1 = N + 1;
        }
        auto start_time = Clock::now();
        if (choice == 1)
        {
            long double n = 2;
            long double r = 1;
            while (1)
            {
                long double rr = (n / r + r) / 2;
                if (rr == r)
                    break;
                r = rr;
            }

            cout << setprecision(digits) << r << endl;
        }
        else if (choice == 2)
        {
            long double e = 2.5;
            long double f = 0.5;
            long double n = 3;
            do
            {
                f /= n;
                long double ee = e + f;
                if (ee == e)
                    break;
                e = ee;
                n += 1;
            } while (1);

            cout << setprecision(digits) << e << endl;
        }
        else if (choice == 3)
            Option3(digits, N);
        else if (choice == 4)
            Option4(digits, N);
        else if (choice == 5)
        {
            for (int n = 8; n <= N; n *= 2)
                Option3(digits, n);
        }
        else if (choice == 6)
        {
            for (int n = 8; n <= N; n *= 2)
                Option4(digits, n);
        }
        auto end_time = Clock::now();
        cout << "runtime in milliseconds = ";
        cout << std::chrono::duration_cast<std::chrono::milliseconds>
            (end_time - start_time).count();
        cout << endl;
        cout << "runtime in nanoseconds  = ";
        cout << std::chrono::duration_cast<std::chrono::nanoseconds>
            (end_time - start_time).count();
        cout << endl;
    }

    return 0;
}

#pragma once

const long double c = 2.0e9;
const long double Pi = 3.1415926535897932384626433832795;

class FourierSeries
{
private:
	static long double f(long double x);
	static long double cosTermFunction(int n, long double x);
	static long double sinTermFunction(int n, long double x);
public:
	static void CreateCosSeries(int N, long double a[]);
	static void CreateSinSeries(int N, long double b[]);
	static long double Series(int N, long double x,
		long double a[], long double b[]);
};

#include <math.h>
#include "FourierSeries.h"
#include "Integral.h"

long double FourierSeries::f(long double x)
{
    return atanl(x);
}

long double FourierSeries::cosTermFunction(int n, long double x)
{
    return cosl(n * x * Pi / c) * f(x);
}

long double FourierSeries::sinTermFunction(int n, long double x)
{
    return sinl(n * x * Pi / c) * f(x);
}

void FourierSeries::CreateCosSeries(int N, long double a[])
{
    long double e[7] = { 0 };

    e[1] = e[2] = 1.0e-12;

    for (int n = 0; n <= N; n++)
        a[n] = Integral::integral(
            n, -c, c, cosTermFunction, e, 1, 1) / c;
}

void FourierSeries::CreateSinSeries(int N, long double b[])
{
    long double e[7] = { 0 };

    e[1] = e[2] = 1.0e-12;

    for (int n = 1; n <= N; n++)
        b[n] = Integral::integral(
            n, -c, c, sinTermFunction, e, 1, 1) / c;
}

long double FourierSeries::Series(int N, long double x,
    long double a[], long double b[])
{
    long double sum = 0.0;

    for (int n = 1; n <= N; n++)
        sum += a[n] * cosl(2.0 * n * x) + b[n] * sinl(2.0 * n * x);

    return a[0] / 2.0 + sum / 2.0;
}

#pragma once

// Translated from C source code found in the tome
// "A Numerical Library in C for Scientists and
// Engineers" by H.T. Lau, PhD

class Integral
{
private:
	static long double integralqad(
		int n,
		int transf, long double (*fx)(int, long double), long double e[],
		long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
		long double* f2, long double re, long double ae, long double b1);
	static void integralint(
		int n,
		int transf, long double (*fx)(int, long double), long double e[],
		long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
		long double* f2, long double* sum, long double re, long double ae, long double b1,
		long double hmin);
public:
	static long double integral(int n, long double a, long double b,
		long double (*fx)(int, long double), long double e[],
		int ua, int ub);
};

#include <math.h>
#include "Integral.h"

long double Integral::integral(
	int n,
	long double a, long double b,
	long double (*fx)(int, long double), long double e[],
	int ua, int ub)
{
	long double x0, x1, x2, f0, f1, f2, re, ae, b1 = 0, x;

	re = e[1];
	if (ub)
		ae = e[2] * 180.0 / fabsl(b - a);
	else
		ae = e[2] * 90.0 / fabsl(b - a);
	if (ua) {
		e[3] = e[4] = 0.0;
		x = x0 = a;
		f0 = (*fx)(n, x);
	}
	else {
		x = x0 = a = e[5];
		f0 = e[6];
	}
	e[5] = x = x2 = b;
	e[6] = f2 = (*fx)(n, x);
	e[4] += integralqad(n, 0, fx, e, &x0, &x1, &x2, &f0, &f1, &f2, re, ae, b1);
	if (!ub) {
		if (a < b) {
			b1 = b - 1.0;
			x0 = 1.0;
		}
		else {
			b1 = b + 1.0;
			x0 = -1.0;
		}
		f0 = e[6];
		e[5] = x2 = 0.0;
		e[6] = f2 = 0.0;
		ae = e[2] * 90.0;
		e[4] -= integralqad(n, 1, fx, e, &x0, &x1, &x2, &f0, &f1, &f2, re, ae, b1);
	}
	return e[4];
}

long double Integral::integralqad(
	int n,
	int transf, long double (*fx)(int, long double), long double e[],
	long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
	long double* f2, long double re, long double ae, long double b1)
{
	/* this function is internally used by INTEGRAL */

	long double sum, hmin, x, z;

	hmin = fabs((*x0) - (*x2)) * re;
	x = (*x1) = ((*x0) + (*x2)) * 0.5;
	if (transf) {
		z = 1.0 / x;
		x = z + b1;
		(*f1) = (*fx)(n, x) * z * z;
	}
	else
		(*f1) = (*fx)(n, x);
	sum = 0.0;
	integralint(n, transf, fx, e, x0, x1, x2, f0, f1, f2, &sum, re, ae, b1, hmin);
	return sum / 180.0;
}

void Integral::integralint(
	int n,
	int transf, long double (*fx)(int, long double), long double e[],
	long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
	long double* f2, long double* sum, long double re, long double ae, long double b1,
	long double hmin)
{
	/* this function is internally used by INTEGRALQAD of INTEGRAL */

	int anew;
	long double x3, x4, f3, f4, h, x, z, v, t;

	x4 = (*x2);
	(*x2) = (*x1);
	f4 = (*f2);
	(*f2) = (*f1);
	anew = 1;
	while (anew) {
		anew = 0;
		x = (*x1) = ((*x0) + (*x2)) * 0.5;
		if (transf) {
			z = 1.0 / x;
			x = z + b1;
			(*f1) = (*fx)(n, x) * z * z;
		}
		else
			(*f1) = (*fx)(n, x);
		x = x3 = ((*x2) + x4) * 0.5;
		if (transf) {
			z = 1.0 / x;
			x = z + b1;
			f3 = (*fx)(n, x) * z * z;
		}
		else
			f3 = (*fx)(n, x);
		h = x4 - (*x0);
		v = (4.0 * ((*f1) + f3) + 2.0 * (*f2) + (*f0) + f4) * 15.0;
		t = 6.0 * (*f2) - 4.0 * ((*f1) + f3) + (*f0) + f4;
		if (fabsl(t) < fabsl(v) * re + ae)
			(*sum) += (v - t) * h;
		else if (fabsl(h) < hmin)
			e[3] += 1.0;
		else {
			integralint(n, transf, fx, e, x0, x1, x2, f0, f1, f2, sum,
				re, ae, b1, hmin);
			*x2 = x3;
			*f2 = f3;
			anew = 1;
		}
		if (!anew) {
			*x0 = x4;
			*f0 = f4;
		}
	}
}
Unknown's avatar

Author: jamespatewilliamsjr

My whole legal name is James Pate Williams, Jr. I was born in LaGrange, Georgia approximately 70 years ago. I barely graduated from LaGrange High School with low marks in June 1971. Later in June 1979, I graduated from LaGrange College with a Bachelor of Arts in Chemistry with a little over a 3 out 4 Grade Point Average (GPA). In the Spring Quarter of 1978, I taught myself how to program a Texas Instruments desktop programmable calculator and in the Summer Quarter of 1978 I taught myself Dayton BASIC (Beginner's All-purpose Symbolic Instruction Code) on LaGrange College's Data General Eclipse minicomputer. I took courses in BASIC in the Fall Quarter of 1978 and FORTRAN IV (Formula Translator IV) in the Winter Quarter of 1979. Professor Kenneth Cooper, a genius poly-scientist taught me a course in the Intel 8085 microprocessor architecture and assembly and machine language. We would hand assemble our programs and insert the resulting machine code into our crude wooden box computer which was designed and built by Professor Cooper. From 1990 to 1994 I earned a Bachelor of Science in Computer Science from LaGrange College. I had a 4 out of 4 GPA in the period 1990 to 1994. I took courses in C, COBOL, and Pascal during my BS work. After graduating from LaGrange College a second time in May 1994, I taught myself C++. In December 1995, I started using the Internet and taught myself client-server programming. I created a website in 1997 which had C and C# implementations of algorithms from the "Handbook of Applied Cryptography" by Alfred J. Menezes, et. al., and some other cryptography and number theory textbooks and treatises.

Leave a comment