Huffman Compression in C# Implemented by James Pate Williams, Jr.

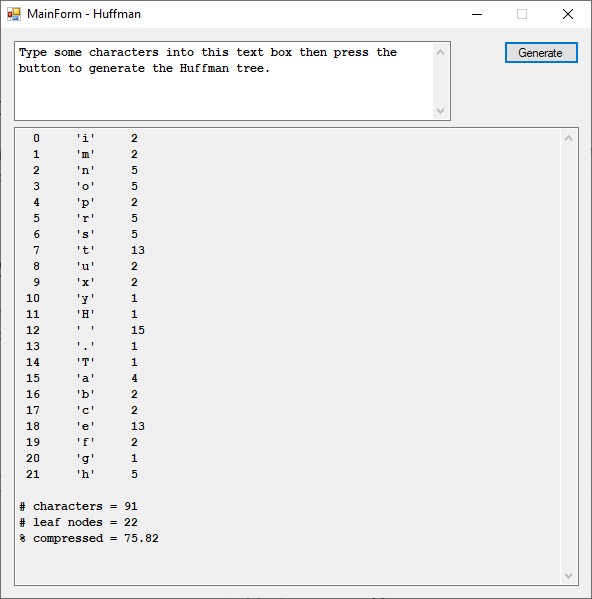
using System;
using System.Collections.Generic;
using System.Windows.Forms;

namespace Huffman
{
    public partial class MainForm : Form
    {
        private int leafNodes;

        public MainForm()
        {
            InitializeComponent();
        }

        private void InorderTraversal(BinaryTreeNode<CharFreq> node)
        {
            if (node != null)
            {
                InorderTraversal(node.Left);

                CharFreq cf = node.Value;
                int ord = (int)cf.ch;

                if (node.Left == null && node.Right == null)
                {
                    textBox2.Text += leafNodes.ToString("F0").PadLeft(3) + '\t';
                    textBox2.Text += "'" + new string(cf.ch, 1) + "' " + '\t';
                    textBox2.Text += node.Value.freq.ToString() + "\r\n";
                    leafNodes++;
                }

                InorderTraversal(node.Right);
            }
        }

        private void button1_Click(object sender, EventArgs e)
        {
            string s = textBox1.Text;
            int n = s.Length;
            List<CharFreq> list = new List<CharFreq>();

            textBox2.Text = string.Empty;

            for (int i = 0; i < n; i++)
            {
                bool found = false;
                char c = s[i];
                CharFreq cf = new CharFreq();

                for (int j = 0; !found && j < list.Count; j++)
                {
                    if (c == list[j].ch)
                    {
                        found = true;
                        cf.ch = c;
                        cf.freq = 1 + list[j].freq;
                        list.RemoveAt(j);
                        list.Add(cf);
                    }
                }

                if (!found)
                {
                    cf.ch = c;
                    cf.freq = 1;
                    list.Add(cf);
                }
            }
                        
            HuffmanTree ht = new HuffmanTree();
            BinaryTreeNode<CharFreq> root = ht.Build(list, list.Count);

            InorderTraversal(root);
            textBox2.Text += "\r\n# characters = " + n.ToString() + "\r\n";
            textBox2.Text += "# leaf nodes = " + leafNodes.ToString() + "\r\n";
            textBox2.Text += "% compressed = " + 
                (100.0 - 100.0 * ((double)leafNodes) / n).ToString("F2") + "\r\n"; 
        }
    }
}

namespace Huffman
{
    public class BinaryTreeNode<T> : Node<T>
    {
        public BinaryTreeNode() : base() { }
        public BinaryTreeNode(T data) : base(data, null) { }
        public BinaryTreeNode(T data, BinaryTreeNode<T> left, BinaryTreeNode<T> right)
        {
            base.Value = data;
            NodeList<T> children = new NodeList<T>(2)
            {
                [0] = left,
                [1] = right
            };

            base.Neighbors = children;
        }

        public BinaryTreeNode<T> Left
        {
            get
            {
                if (base.Neighbors == null)
                    return null;
                else
                    return (BinaryTreeNode<T>)base.Neighbors[0];
            }
            set
            {
                if (base.Neighbors == null)
                    base.Neighbors = new NodeList<T>(2);

                base.Neighbors[0] = value;
            }
        }

        public BinaryTreeNode<T> Right
        {
            get
            {
                if (base.Neighbors == null)
                    return null;
                else
                    return (BinaryTreeNode<T>)base.Neighbors[1];
            }
            set
            {
                if (base.Neighbors == null)
                    base.Neighbors = new NodeList<T>(2);

                base.Neighbors[1] = value;
            }
        }
    }
}

using System.Collections.Generic;

namespace Huffman
{
    public class HuffmanTree
    {
        public BinaryTreeNode<CharFreq> Build(List<CharFreq> charFreq, int n)
        {
            PriorityQueue Q = new PriorityQueue();

            for (int i = 0; i < n; i++)
            {
                BinaryTreeNode<CharFreq> z = new BinaryTreeNode<CharFreq>(charFreq[i]);

                Q.insert(z);
            }

            Q.buildHeap();

            for (int i = 0; i < n - 1; i++)
            {
                BinaryTreeNode<CharFreq> x = Q.extractMin();
                BinaryTreeNode<CharFreq> y = Q.extractMin();
                CharFreq chFreq = new CharFreq();

                chFreq.ch = (char)((int)x.Value.ch + (int)y.Value.ch);
                chFreq.freq = x.Value.freq + y.Value.freq;

                BinaryTreeNode<CharFreq> z = new BinaryTreeNode<CharFreq>(chFreq);

                z.Left = x;
                z.Right = y;
                Q.insert(z);
            }

            return Q.extractMin();
        }
    }
}

namespace Huffman
{
    public class Node<T>
    {
        // Private member-variables
        private T data;
        private NodeList<T> neighbors = null;

        public Node() { }
        public Node(T data) : this(data, null) { }
        public Node(T data, NodeList<T> neighbors)
        {
            this.data = data;
            this.neighbors = neighbors;
        }

        public T Value
        {
            get
            {
                return data;
            }
            set
            {
                data = value;
            }
        }

        protected NodeList<T> Neighbors
        {
            get
            {
                return neighbors;
            }
            set
            {
                neighbors = value;
            }
        }
    }
}

using System.Collections.ObjectModel;

namespace Huffman
{
    public class NodeList<T> : Collection<Node<T>>
    {
        public NodeList() : base() { }

        public NodeList(int initialSize)
        {
            // Add the specified number of items
            for (int i = 0; i < initialSize; i++)
                base.Items.Add(default(Node<T>));
        }

        public Node<T> FindByValue(T value)
        {
            // search the list for the value
            foreach (Node<T> node in Items)
                if (node.Value.Equals(value))
                    return node;

            // if we reached here, we didn't find a matching node
            return null;
        }
    }
}

using System.Collections.Generic;

namespace Huffman
{
    public struct CharFreq
    {
        public char ch;
        public int freq;
    }

    public class PriorityQueue
    {
        int heapSize;
        List<BinaryTreeNode<CharFreq>> nodeList;

        public List<BinaryTreeNode<CharFreq>> NodeList
        {
            get
            {
                return nodeList;
            }
        }

        public PriorityQueue()
        {
            nodeList = new List<BinaryTreeNode<CharFreq>>();
        }

        public PriorityQueue(List<BinaryTreeNode<CharFreq>> nl)
        {
            heapSize = nl.Count;
            nodeList = new List<BinaryTreeNode<CharFreq>>();

            for (int i = 0; i < nl.Count; i++)
                nodeList.Add(nl[i]);
        }

        public void exchange(int i, int j)
        {
            BinaryTreeNode<CharFreq> temp = nodeList[i];

            nodeList[i] = nodeList[j];
            nodeList[j] = temp;
        }

        public void heapify(int i)
        {
            int l = 2 * i + 1;
            int r = 2 * i + 2;
            int largest = -1;

            if (l < heapSize && nodeList[l].Value.ch > nodeList[i].Value.ch)
                largest = l;
            else
                largest = i;
            if (r < heapSize && nodeList[r].Value.ch > nodeList[largest].Value.ch)
                largest = r;
            if (largest != i)
            {
                exchange(i, largest);
                heapify(largest);
            }
        }

        public void buildHeap()
        {
            for (int i = heapSize / 2; i >= 0; i--)
                heapify(i);
        }

        public int size()
        {
            return heapSize;
        }

        public BinaryTreeNode<CharFreq> elementAt(int i)
        {
            return nodeList[i];
        }

        public void heapSort()
        {
            int temp = heapSize;

            buildHeap();

            for (int i = heapSize - 1; i >= 1; i--)
            {
                exchange(0, i);
                heapSize--;
                heapify(0);
            }

            heapSize = temp;
        }

        public BinaryTreeNode<CharFreq> extractMin()
        {
            if (heapSize < 1)
                return null;

            heapSort();

            exchange(0, heapSize - 1);
            heapSize--;

            BinaryTreeNode<CharFreq> node = nodeList[heapSize];

            nodeList.RemoveAt(heapSize);
            heapSize = nodeList.Count;
            return node;
        }

        public void insert(BinaryTreeNode<CharFreq> node)
        {
            nodeList.Add(node);
            heapSize = nodeList.Count;
            buildHeap();
        }
    }
}