using System;
using System.Windows.Forms;
namespace NumericalDifferentiation
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
comboBox1.SelectedIndex = 0;
}
private double F1(double x)
{
return x * (x * (x - 2) + 4) - 1;
}
private double F2(double x)
{
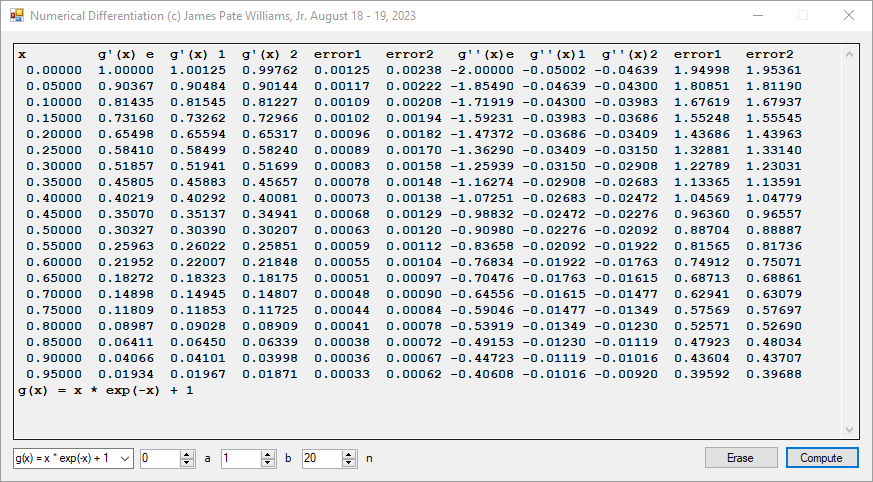
return x * Math.Exp(-x) + 1;
}
private double F3(double x)
{
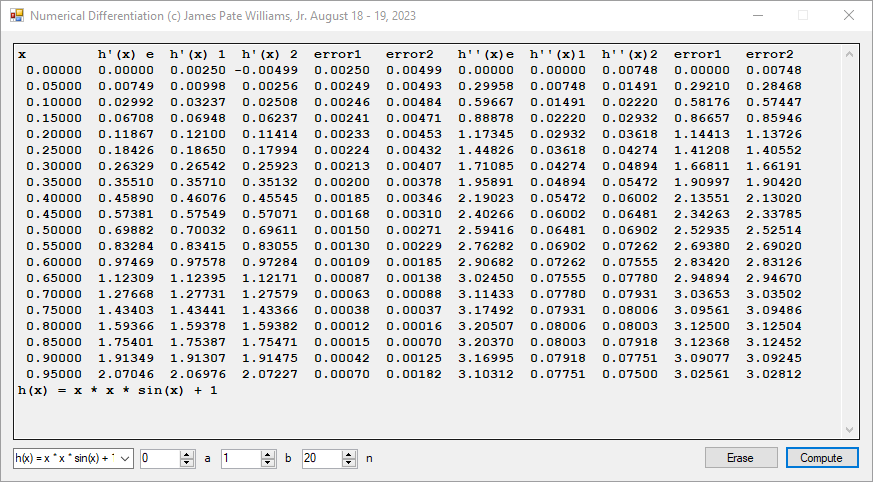
return x * x * Math.Sin(x) + 1;
}
private double DF1(double x)
{
return 3 * x * x - 4 * x + 4;
}
private double DF2(double x)
{
return Math.Exp(-x) - x * Math.Exp(-x);
}
private double DF3(double x)
{
return 2 * x * Math.Sin(x) + x * x * Math.Cos(x);
}
private double DDF1(double x)
{
return 6 * x - 4;
}
private double DDF2(double x)
{
return -2 * Math.Exp(-x) + x * Math.Exp(-x);
}
private double DDF3(double x)
{
return
2 * Math.Sin(x) + 2 * x * Math.Cos(x) +
2 * x * Math.Cos(x) - x * x * Math.Sin(x);
}
private void button1_Click(object sender, EventArgs e)
{
double a = (double)numericUpDown1.Value;
double b = (double)numericUpDown2.Value;
int n = (int)numericUpDown3.Value;
double deriv1c, deriv1f;
double deriv2c, deriv2f;
double x = a, y, u, v;
double error1c, error1f, error2c, error2f;
double h = (b - a) / n;
if (comboBox1.SelectedIndex == 0)
textBox1.Text += "x\t f'(x) e f'(x) 1 f'(x) 2 " +
"error1 error2 f''(x)e f''(x)1 f''(x)2 " +
"error1 error2\r\n";
else if (comboBox1.SelectedIndex == 1)
textBox1.Text += "x\t g'(x) e g'(x) 1 g'(x) 2 " +
"error1 error2 g''(x)e g''(x)1 g''(x)2 " +
"error1 error2\r\n";
else if (comboBox1.SelectedIndex == 2)
textBox1.Text += "x\t h'(x) e h'(x) 1 h'(x) 2 " +
"error1 error2 h''(x)e h''(x)1 h''(x)2 " +
"error1 error2\r\n";
while (x <= b)
{
switch (comboBox1.SelectedIndex)
{
case 0:
y = F1(x);
u = DF1(x);
v = DDF1(x);
deriv1c = Differentiation.Derivative1sc(x, h, F1);
deriv1f = Differentiation.Derivative1sf(x, h, F1);
deriv2c = Differentiation.Derivative2sc(x, h, F1);
deriv2f = Differentiation.Derivative2sf(x, h, F1);
error1c = Math.Abs(deriv1c - u);
error1f = Math.Abs(deriv1f - u);
error2c = Math.Abs(deriv2c - v);
error2f = Math.Abs(deriv2f - v);
textBox1.Text +=
x.ToString("F5").PadLeft(8) + " " +
u.ToString("F5").PadLeft(8) + " " +
deriv1c.ToString("F5").PadLeft(8) + " " +
deriv1f.ToString("F5").PadLeft(8) + " " +
error1c.ToString("F5").PadLeft(8) + " " +
error1f.ToString("F5").PadLeft(8) + " " +
v.ToString("F5").PadLeft(8) + " " +
deriv2c.ToString("F5").PadLeft(8) + " " +
deriv2f.ToString("F5").PadLeft(8) + " " +
error2c.ToString("F5").PadLeft(8) + " " +
error2f.ToString("F5").PadLeft(8) + "\r\n";
break;
case 1:
y = F2(x);
u = DF2(x);
v = DDF2(x);
deriv1c = Differentiation.Derivative1sc(x, h, F2);
deriv1f = Differentiation.Derivative1sf(x, h, F2);
deriv2c = Differentiation.Derivative2sc(x, h, F2);
deriv2f = Differentiation.Derivative2sf(x, h, F2);
error1c = Math.Abs(deriv1c - u);
error1f = Math.Abs(deriv1f - u);
error2c = Math.Abs(deriv2c - v);
error2f = Math.Abs(deriv2f - v);
textBox1.Text +=
x.ToString("F5").PadLeft(8) + " " +
u.ToString("F5").PadLeft(8) + " " +
deriv1c.ToString("F5").PadLeft(8) + " " +
deriv1f.ToString("F5").PadLeft(8) + " " +
error1c.ToString("F5").PadLeft(8) + " " +
error1f.ToString("F5").PadLeft(8) + " " +
v.ToString("F5").PadLeft(8) + " " +
deriv2c.ToString("F5").PadLeft(8) + " " +
deriv2f.ToString("F5").PadLeft(8) + " " +
error2c.ToString("F5").PadLeft(8) + " " +
error2f.ToString("F5").PadLeft(8) + "\r\n";
break;
case 2:
y = F3(x);
u = DF3(x);
v = DDF3(x);
deriv1c = Differentiation.Derivative1sc(x, h, F3);
deriv1f = Differentiation.Derivative1sf(x, h, F3);
deriv2c = Differentiation.Derivative2sc(x, h, F3);
deriv2f = Differentiation.Derivative2sf(x, h, F3);
error1c = Math.Abs(deriv1c - u);
error1f = Math.Abs(deriv1f - u);
error2c = Math.Abs(deriv2c - v);
error2f = Math.Abs(deriv2f - v);
textBox1.Text +=
x.ToString("F5").PadLeft(8) + " " +
u.ToString("F5").PadLeft(8) + " " +
deriv1c.ToString("F5").PadLeft(8) + " " +
deriv1f.ToString("F5").PadLeft(8) + " " +
error1c.ToString("F5").PadLeft(8) + " " +
error1f.ToString("F5").PadLeft(8) + " " +
v.ToString("F5").PadLeft(8) + " " +
deriv2c.ToString("F5").PadLeft(8) + " " +
deriv2f.ToString("F5").PadLeft(8) + " " +
error2c.ToString("F5").PadLeft(8) + " " +
error2f.ToString("F5").PadLeft(8) + "\r\n";
break;
default:
break;
}
x += h;
}
textBox1.Text += comboBox1.SelectedItem;
}
private void button2_Click(object sender, EventArgs e)
{
textBox1.Text = string.Empty;
}
}
}
// Derivative formulas translated from FORTRAN 77
// source code found in "Elementary Numerical Analysis:
// An Algorithmic Approach" by S. D. Conte and Carl de
// Boor. Translator: James Pate Williams, Jr. (c)
// August 18 - 19, 2023
using System;
namespace NumericalDifferentiation
{
// Numerically compute first and second
// ordinary derivatives
class Differentiation
{
static public double Derivative1sc(
double a, double h, Func<double, double> f)
{
return (f(a + h) - f(a - h)) / (h + h);
}
static public double Derivative1sf(
double a, double h, Func<double, double> f)
{
return (-3.0 * f(a) + 4.0 * f(a + h) - f(a + h + h)) / (h + h);
}
static public double Derivative2sc(
double a, double h, Func<double, double> f)
{
return (f(a - h) - 2.0 * f(a) + f(a + h)) / (h + h);
}
static public double Derivative2sf(
double a, double h, Func<double, double> f)
{
return (f(a) - 2.0 * f(a + h) + f(a + h + h)) / (h + h);
}
}
}
Author: jamespatewilliamsjr
My whole legal name is James Pate Williams, Jr. I was born in LaGrange, Georgia approximately 70 years ago. I barely graduated from LaGrange High School with low marks in June 1971. Later in June 1979, I graduated from LaGrange College with a Bachelor of Arts in Chemistry with a little over a 3 out 4 Grade Point Average (GPA). In the Spring Quarter of 1978, I taught myself how to program a Texas Instruments desktop programmable calculator and in the Summer Quarter of 1978 I taught myself Dayton BASIC (Beginner's All-purpose Symbolic Instruction Code) on LaGrange College's Data General Eclipse minicomputer. I took courses in BASIC in the Fall Quarter of 1978 and FORTRAN IV (Formula Translator IV) in the Winter Quarter of 1979. Professor Kenneth Cooper, a genius poly-scientist taught me a course in the Intel 8085 microprocessor architecture and assembly and machine language. We would hand assemble our programs and insert the resulting machine code into our crude wooden box computer which was designed and built by Professor Cooper. From 1990 to 1994 I earned a Bachelor of Science in Computer Science from LaGrange College. I had a 4 out of 4 GPA in the period 1990 to 1994. I took courses in C, COBOL, and Pascal during my BS work. After graduating from LaGrange College a second time in May 1994, I taught myself C++. In December 1995, I started using the Internet and taught myself client-server programming. I created a website in 1997 which had C and C# implementations of algorithms from the "Handbook of Applied Cryptography" by Alfred J. Menezes, et. al., and some other cryptography and number theory textbooks and treatises.
View all posts by jamespatewilliamsjr