Brute Force Elliptic Curve Point Counting Algorithm Implementation by James Pate Williams, Jr.

#include <algorithm>
#include <iomanip>
#include <iostream>
#include <chrono>
#include <vector>
using namespace std;

typedef long long ll;

typedef struct ecPoint
{
	ll x, y;
} ECPOINT, *PECPOINT;

typedef struct ecPointOrder
{
	ll order;
	ECPOINT pt;
} ECPOINTORDER, * PECPOINTORDER;

int JACOBI(ll a, ll n)
{
	int e = 0, s;
	ll a1, b = a, m, n1;

	if (a == 0) return 0;
	if (a == 1) return 1;
	while ((b & 1) == 0)
	{
		b >>= 1;
		e++;
	}
	a1 = b;
	m = n % 8;
	if (!(e & 1)) s = 1;
	else if (m == 1 || m == 7) s = +1;
	else if (m == 3 || m == 5) s = -1;
	if (n % 4 == 3 && a1 % 4 == 3) s = -s;
	if (a1 != 1) n1 = n % a1; else n1 = 1;
	return s * JACOBI(n1, a1);
}

ll ExpMod(ll x, ll b, ll n)
/* returns x ^ b mod n */
{
	ll a = 1LL, s = x;

	if (b == 0)
		return 1LL;
	while (b != 0) {
		if (b & 1l) a = (a * s) % n;
		b >>= 1;
		if (b != 0) s = (s * s) % n;
	}
	if (a < 0)
		a += n;
	return a;
}

ll ExtendedEuclidean(ll b, ll n)
{
	ll b0 = b, n0 = n, t = 1, t0 = 0, temp, q, r;

	q = n0 / b0;
	r = n0 - q * b0;

	while (r > 0) {
		temp = t0 - q * t;
		if (temp >= 0) temp = temp % n;
		else temp = n - (-temp % n);
		t0 = t;
		t = temp;
		n0 = b0;
		b0 = r;
		q = n0 / b0;
		r = n0 - q * b0;
	}
	if (b0 != 1) return 0;
	else return t % n;
}

ll Weierstrass(ll a, ll b, ll x, ll p)
{
	return ((((x * x) % p) * x) % p + (a * x) % p + b) % p;
}

ll EPoints(
	bool print,
	ll a, ll b, ll p,
	vector<ECPOINT>& e)
	/* returns the number of points on the elliptic
	curve y ^ 2 = x ^ 3 + ax + b mod p */
{
	ll count = 0, m = (p + 1) / 4, x, y;
	ECPOINT pt{};

	if (p % 4 == 3) {
		for (x = 0; x < p; x++) {
			y = Weierstrass(a, b, x, p);
			if (JACOBI(y, p) != -1) {
				y = ExpMod(y, m, p);
				if (print)
				{
					cout << "(" << setw(2) << x << ", ";
					cout << y << ") " << endl;
				}
				pt.x = x;
				pt.y = y;
				e.push_back(pt);
				count++;
				y = -y % p;
				if (y < 0) y += p;
				if (y != 0)
				{
					if (print)
					{
						cout << "(" << setw(2) << x << ", ";
						cout << y << ") " << endl;
					}
					pt.x = x;
					pt.y = y;
					e.push_back(pt);
					count++;
				}
				if (print && count % 5 == 0)
					cout << endl;
			}
		}
		if (print && count % 5 != 0)
			cout << endl;
	}
	return count;
}

void Add(ll a, ll p, ECPOINT P,
	ECPOINT Q, ECPOINT& R)
	/* elliptic curve point partial addition */
{
	ll i, lambda;

	if (P.x == Q.x && P.y == 0 && Q.y == 0) {
		R.x = 0;
		R.y = 1;
		return;
	}
	if (P.x == Q.x && P.y == p - Q.y) {
		R.x = 0;
		R.y = 1;
		return;
	}
	if (P.x == 0 && P.y == 1) {
		R = Q;
		return;
	}
	if (Q.x == 0 && Q.y == 1) {
		R = P;
		return;
	}
	if (P.x != Q.x) {
		i = Q.x - P.x;
		if (i < 0) i += p;
		i = ExtendedEuclidean(i, p);
		lambda = ((Q.y - P.y) * i) % p;
	}
	else {
		i = ExtendedEuclidean((2 * P.y) % p, p);
		lambda = ((3 * P.x * P.x + a) * i) % p;
	}
	if (lambda < 0) lambda += p;
	R.x = (lambda * lambda - P.x - Q.x) % p;
	R.y = (lambda * (P.x - R.x) - P.y) % p;
	if (R.x < 0) R.x += p;
	if (R.y < 0) R.y += p;
}

void Multiply(
	ll a, ll k, ll p,
	ECPOINT P,
	ECPOINT& R)
{
	ECPOINT S;

	R.x = 0;
	R.y = 1;
	S = P;
	while (k != 0) {
		if (k & 1) Add(a, p, R, S, R);
		k >>= 1;
		if (k != 0) Add(a, p, S, S, S);
	}
}

ll Order(ll a, ll p, ECPOINT P)
{
	ll order = 1;
	ECPOINT Q = P, R{};

	do {
		order++;
		Add(a, p, P, Q, R);
		Q = R;
	} while (R.x != 0 && R.y != 1);
	return order;
}

const int PrimeSize = 10000000;
bool sieve[PrimeSize];

void PopulateSieve() {

	// sieve of Eratosthenes

	int c, inc, i, n = PrimeSize - 1;

	for (i = 0; i < n; i++)
		sieve[i] = false;

	sieve[1] = false;
	sieve[2] = true;

	for (i = 3; i <= n; i++)
		sieve[i] = (i & 1) == 1 ? true : false;

	c = 3;

	do {
		i = c * c;
		inc = c + c;

		while (i <= n) {
			sieve[i] = false;
			i += inc;
		}

		c += 2;
		while (!sieve[c])
			c++;
	} while (c * c <= n);
}

ll Partition(
	vector<ECPOINTORDER>& a, ll n, ll lo, ll hi)
{
	ll pivotIndex = lo + (hi - lo) / 2;
	ECPOINTORDER po = a[(unsigned int)pivotIndex];
	ECPOINTORDER x = po;
	ECPOINTORDER t = x;

	a[(unsigned int)pivotIndex] = a[(unsigned int)hi];
	a[(unsigned int)hi] = t;

	ll storeIndex = lo;

	for (unsigned int i = (unsigned int)lo; i < (unsigned int)hi; i++)
	{
		if (a[i].order < x.order)
		{
			t = a[i];
			a[i] = a[(unsigned int)storeIndex];
			a[(unsigned int)(storeIndex++)] = t;
		}
	}

	t = a[(unsigned int)storeIndex];
	a[(unsigned int)storeIndex] = a[(unsigned int)hi];
	a[(unsigned int)hi] = t;

	return storeIndex;
}

static void DoQuickSort(
	vector<ECPOINTORDER>& a, ll n, ll p, ll r)
{
	if (p < r)
	{
		ll q = Partition(a, n, p, r);

		DoQuickSort(a, n, p, q - 1);
		DoQuickSort(a, n, q + 1, r);
	}
}

void QuickSort(vector<ECPOINTORDER>& a, ll n)
{
	DoQuickSort(a, n, 0, n - 1);
}

int main()
{
	PopulateSieve();

	while (true)
	{
		bool noncyclic = false;
		int option;
		ll a, b, p;

		cout << "Enter 1 to continue or 0 to quit = ";
		cin >> option;

		if (option == 0)
			break;

		cout << "Weierstrass parameter a = ";
		cin >> a;
		cout << "Weierstrass parameter b = ";
		cin >> b;
		cout << "Enter the prime parameter p = ";
		cin >> p;

		if (!sieve[p])
		{
			cout << "p is not a prime number. " << endl;
			continue;
		}

		if (p % 4 != 3)
		{
			cout << "p mod 4 must be 3 for this algorithm." << endl;
			continue;
		}

		bool print = false, enumerate = false;
		vector<ECPOINT> e;
		vector<ECPOINTORDER> eOrder;

		cout << "Enumerate points (0 for no or 1 for yes)? ";
		cin >> option;

		enumerate = option == 1;
		auto time0 = chrono::high_resolution_clock::now();
		ll count = EPoints(print, a, b, p, e);
		auto time1 = chrono::high_resolution_clock::now();
		auto elapsed = time1 - time0;
		ll h = count + 1;
		ll maxOrder = 0;
		ll minOrder = h;
		ll order = -1;
		ECPOINT P{}, Q{};

		if (enumerate)
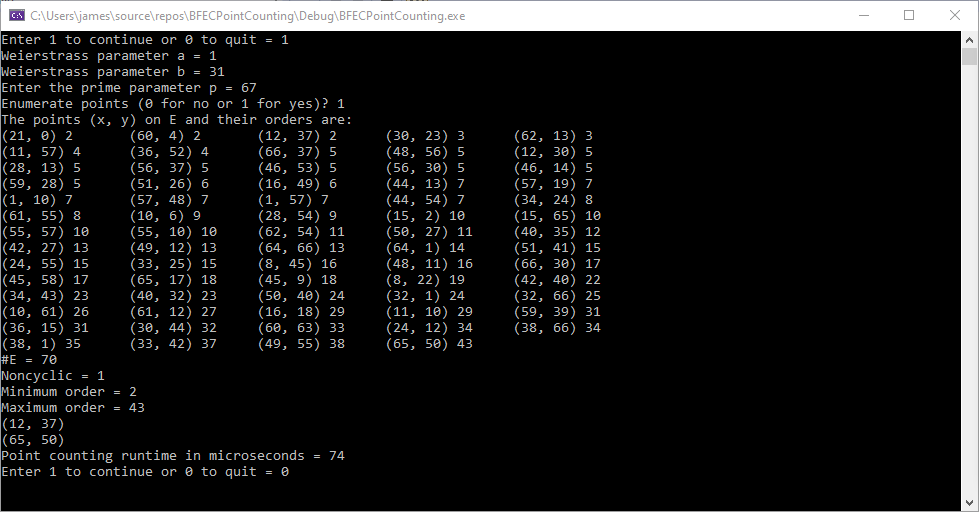
			cout << "The points (x, y) on E and their orders are:" << endl;

		for (unsigned int i = 0; i < count; i++)
		{
			ECPOINTORDER ptOrder{};

			order = Order(a, p, e[i]);
			ptOrder.order = order;
			ptOrder.pt = e[i];
			eOrder.push_back(ptOrder);

			if (order < h)
				noncyclic = true;
			if (order < minOrder) {
				P = e[i];
				minOrder = order;
			}
			if (order > maxOrder) {
				Q = e[i];
				maxOrder = order;
			}
		}
		if (enumerate)
		{
			QuickSort(eOrder, count);

			for (unsigned int i = 0; i < eOrder.size(); i++)
			{
				cout << "(" << eOrder[i].pt.x << ", ";
				cout << eOrder[i].pt.y << ") ";
				cout << eOrder[i].order << "\t";
				if ((i + 1) % 5 == 0)
					cout << endl;
			}
			if (count % 5 != 0)
				cout << endl;
		}
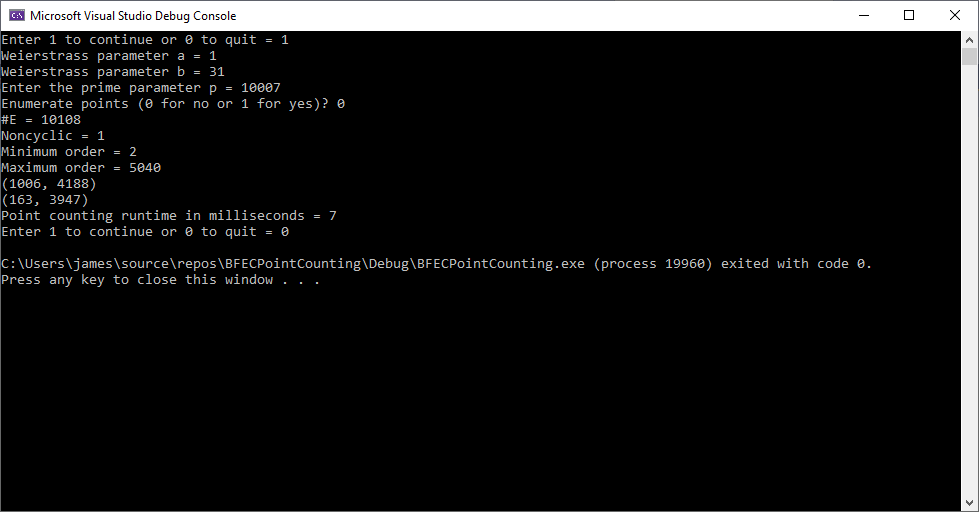
		cout << "#E = " << h << endl;
		cout << "Noncyclic = " << noncyclic << endl;
		cout << "Minimum order = " << minOrder << endl;
		cout << "Maximum order = " << maxOrder << endl;
		cout << "(" << P.x << ", " << P.y << ")" << endl;
		cout << "(" << Q.x << ", " << Q.y << ")" << endl;

		long long runtime = chrono::duration_cast<chrono::milliseconds>(elapsed).count();
		if (runtime != 0)
			cout << "Point counting runtime in milliseconds = " << runtime << endl;
		else
		{
			runtime = chrono::duration_cast<chrono::microseconds>(elapsed).count();
			cout << "Point counting runtime in microseconds = " << runtime << endl;
		}
	}
	return 0;
}