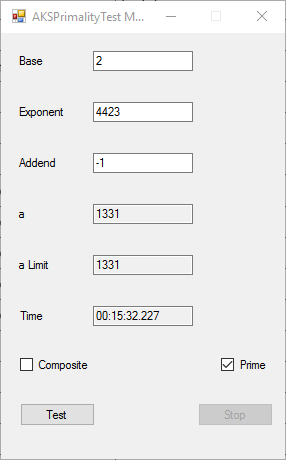
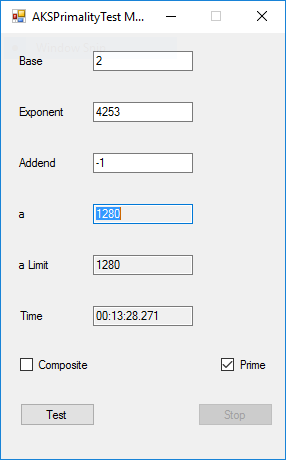
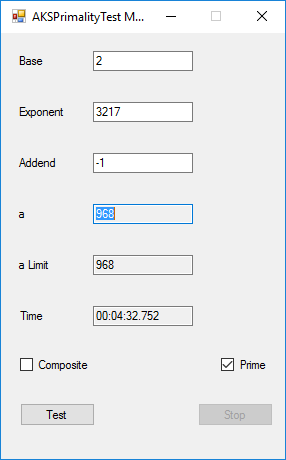
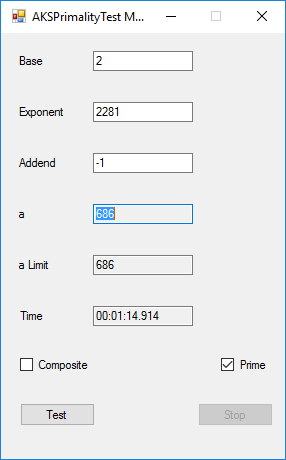
This application implements the algorithm described in the paper at the URL http://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf. I replaced Step 1 of the algorithm with the Miller-Rabin probabilistic primality test. If that test shows that the number is composite, I return the value COMPOSITE. This algorithm is much easier to implement and understand that Wieb Bosmer’s Primality Proving with Cyclotomy also known as the Jacobi sums primality test. As a test we determine that the following Mersenne numbers are prime: M_1279, M_2203, M_2281, M_3217, and M_4253 where M_n = 2 ^ n – 1, and the primes have 386, 664, 687, 969, and 1281 decimal digits, respectively. M_1279 was first proven prime by Raphael M. Robinson on June 25, 1952, using the Lucas-Lehmer test on a SWAC computer. The same author found that M_2203 was prime on October 7, 1952, and M_2281 was prime on October 9, 1952, using the same method and computer. Hans Riesel determined that M_3217 was prime on September 8, 1957, using the Lucas-Lehmer test on a BESK computer. M_4253 was proven prime on November 3, 1961 by Alexander Hurwitz using the Lucas-Lehmer test on an IBM 7090 mainframe computer. See http://www.mersenne.org/primes/ for many more Mersenne primes. All of the computations illustrated below were performed on a late November 2015 Dell XPS 8900 computer with 16 GB RAM Intel(R) Core(TM) i7-6700K CPU @ 4.00 GHz running Windows 10 Pro. The .Net framework is .Net 4.5.2. This is a multitasking version of the original BigInteger variant of the application. Someone with a quad core CPU with 8 virtual processors can try NumberTasks = 8 to see if that speeds up this application more or less. I usually try to limit the number of tasks to actual number of cores.