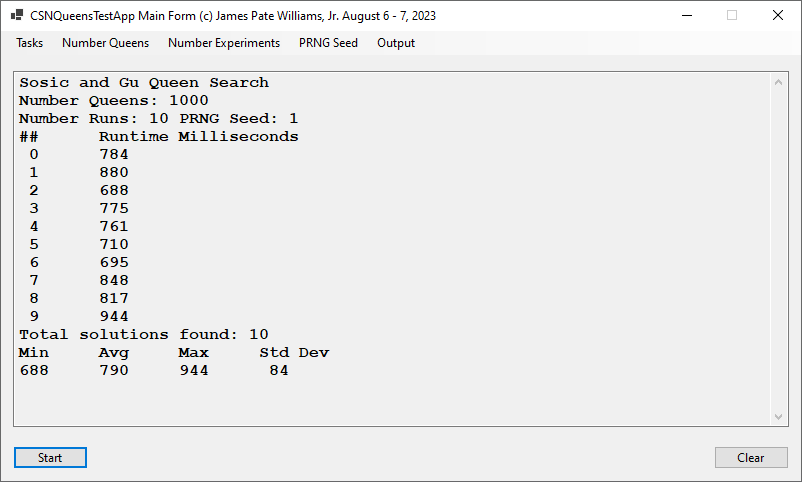
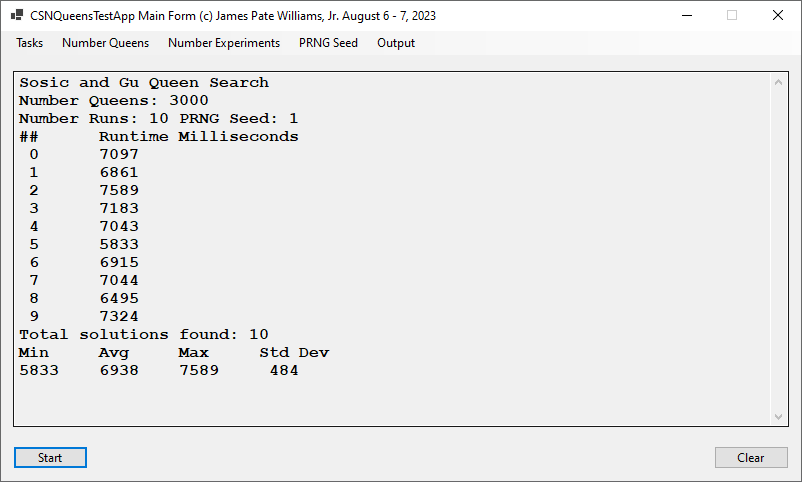
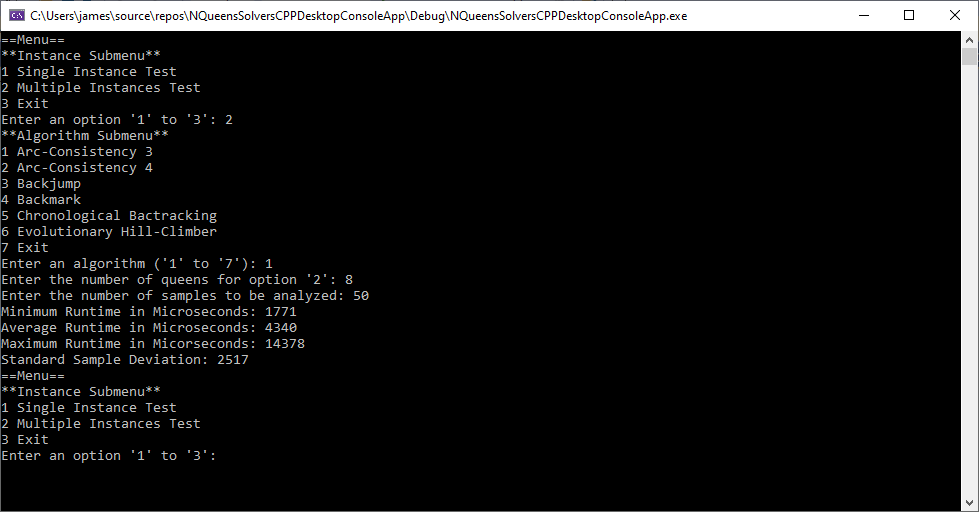
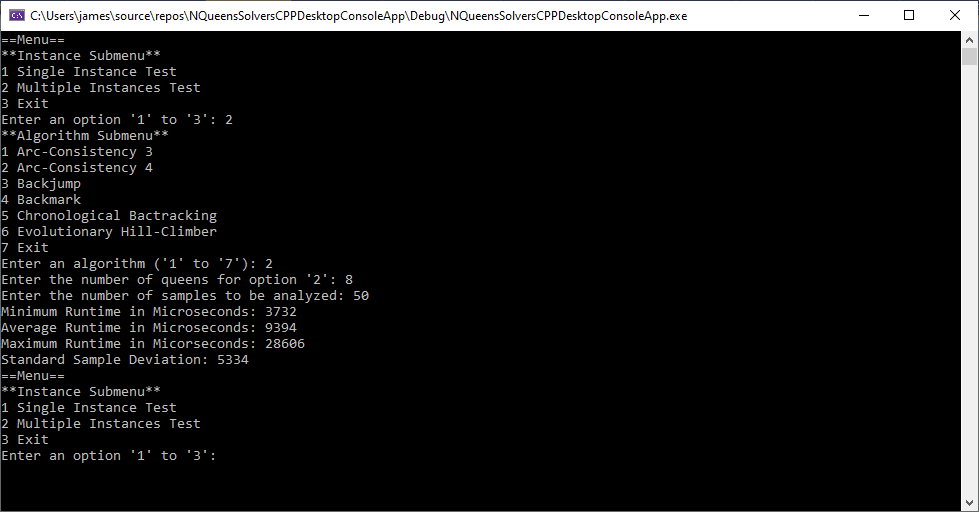
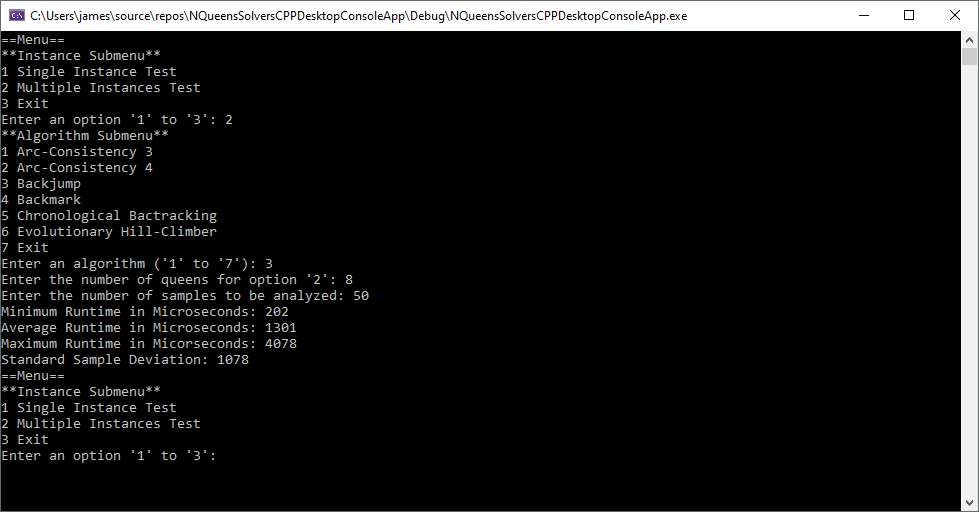
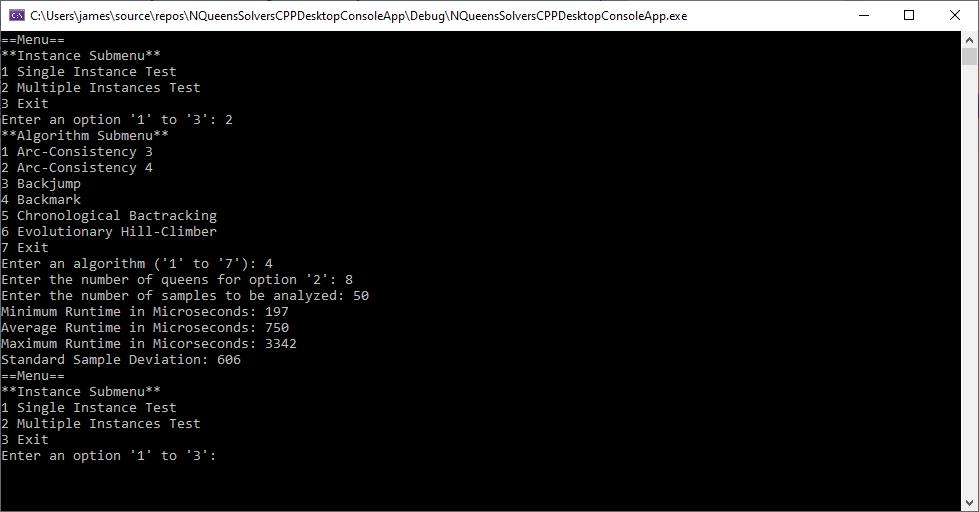
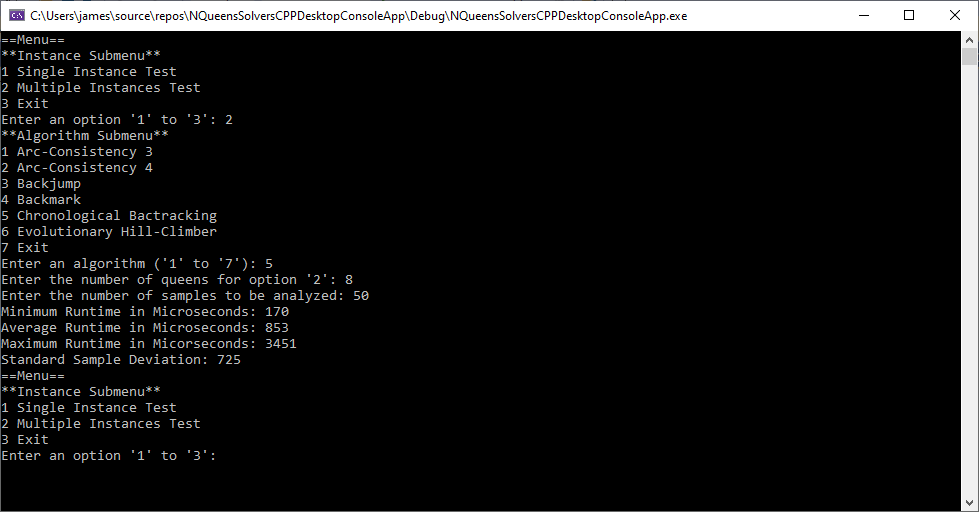
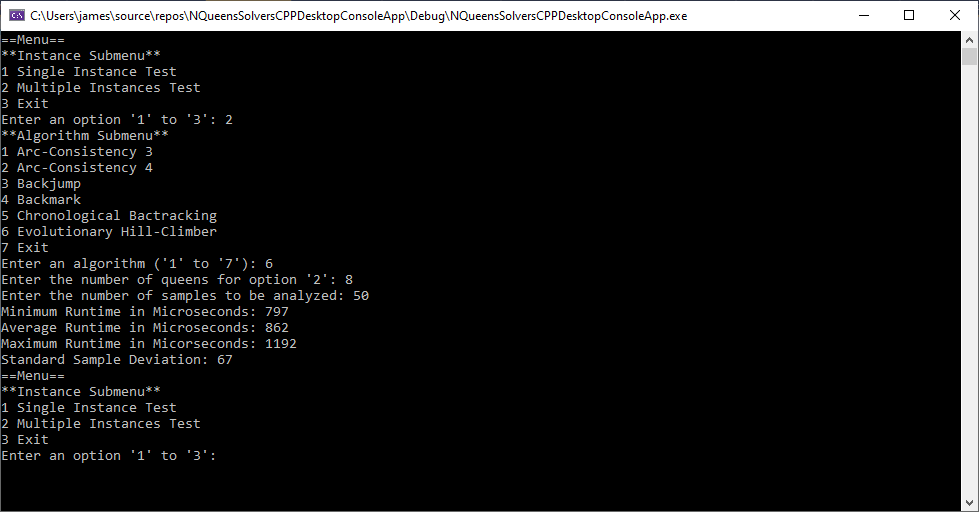
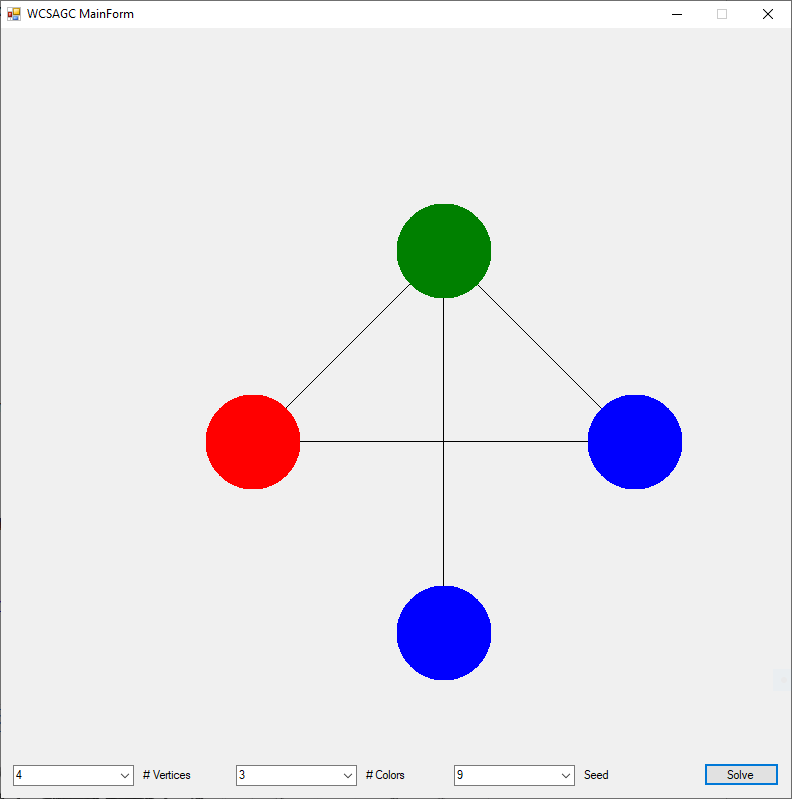
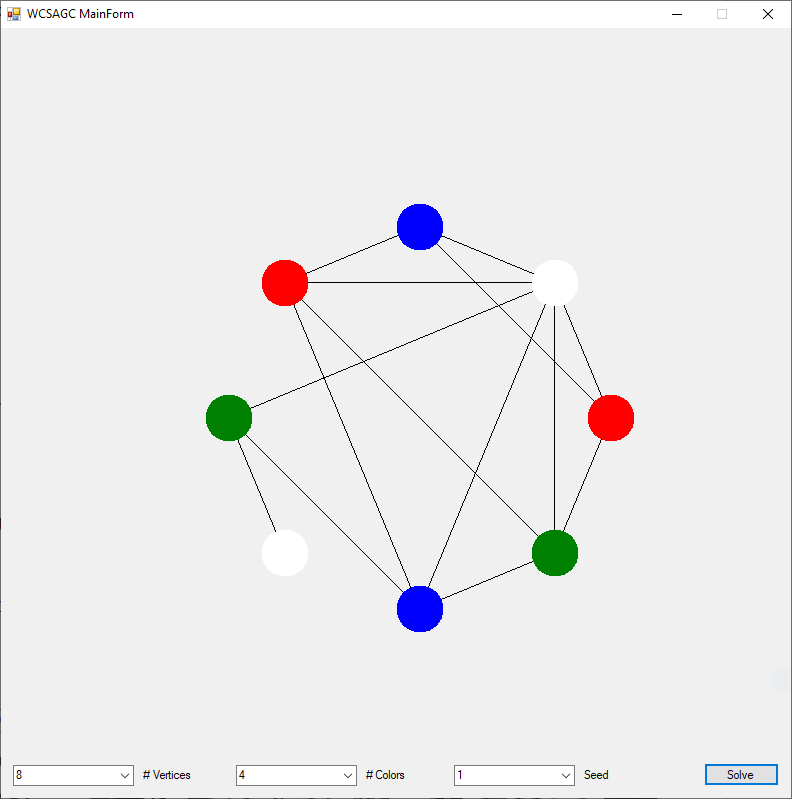
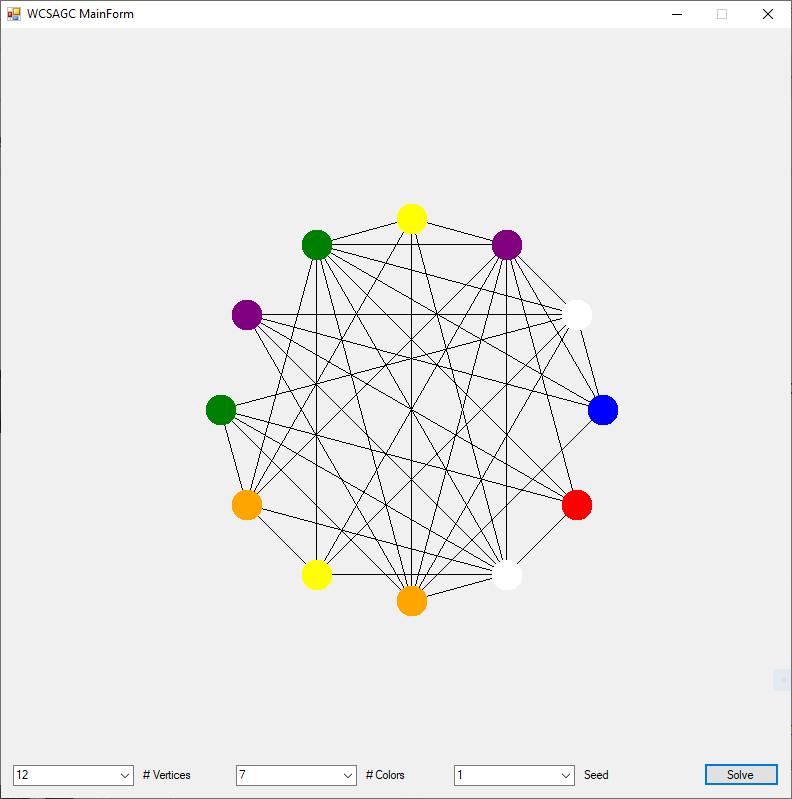
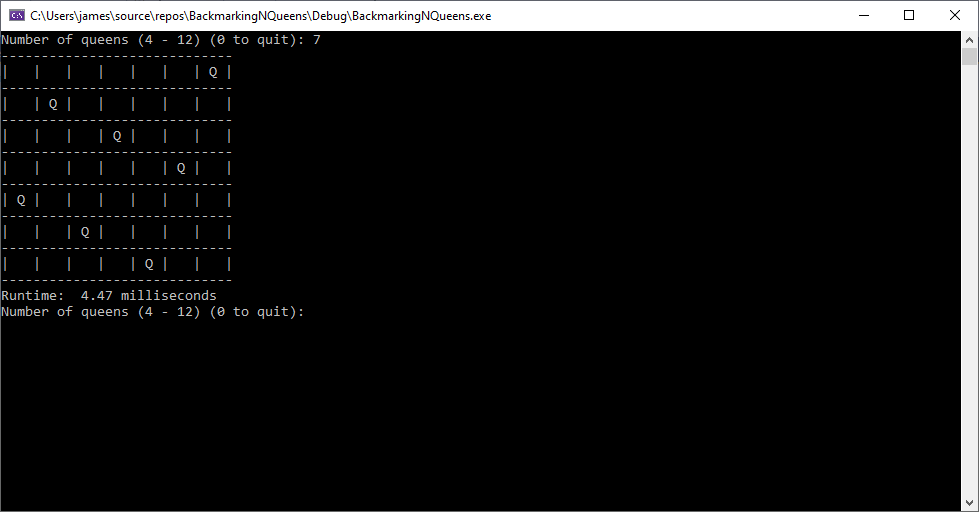
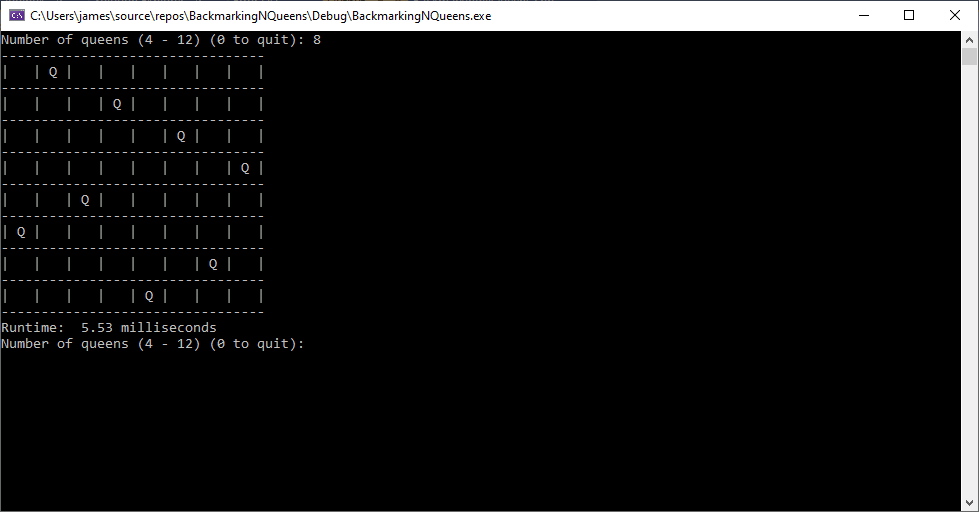
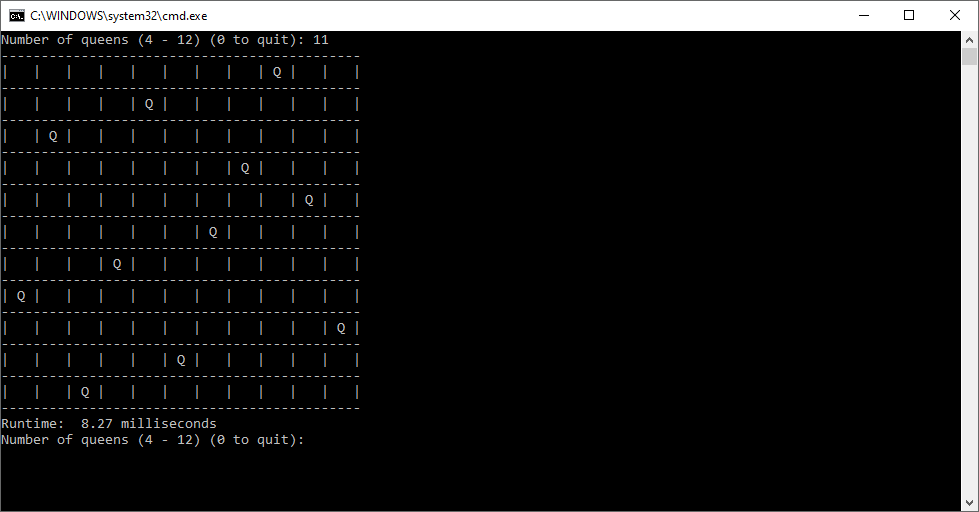
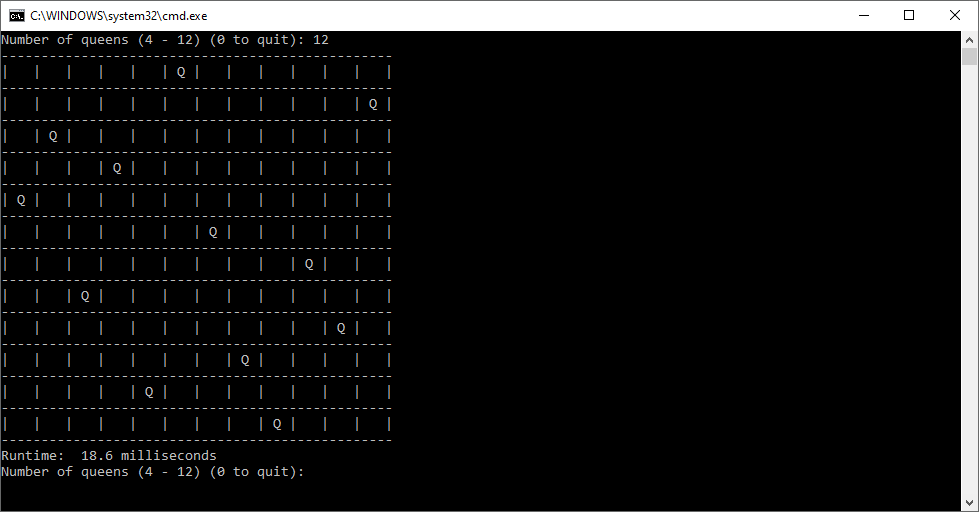
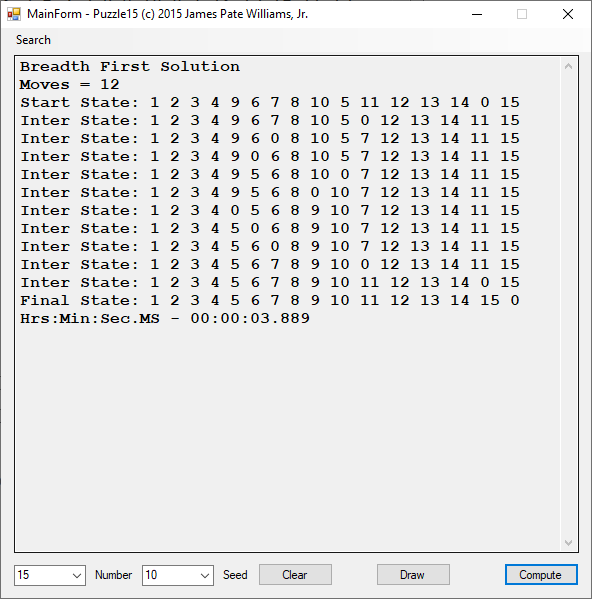
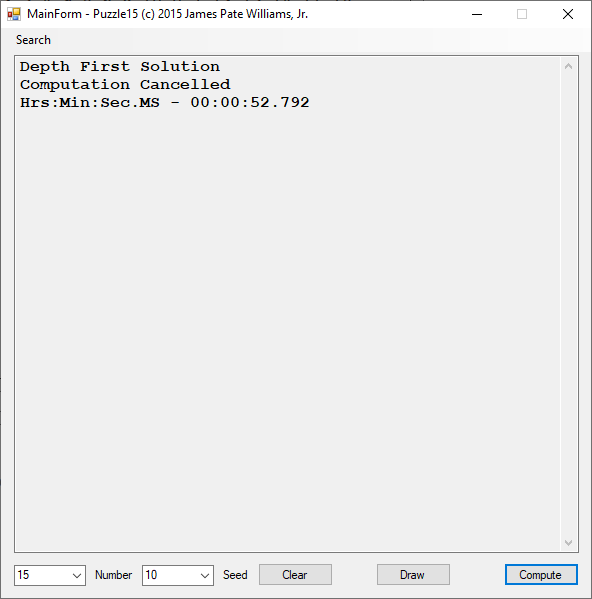
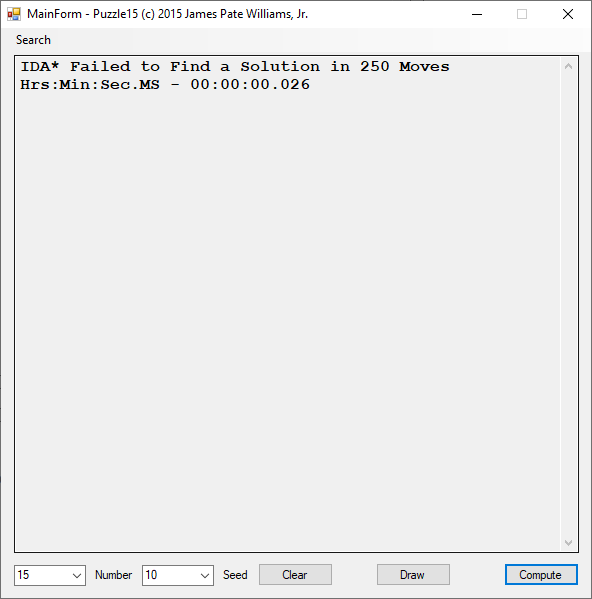
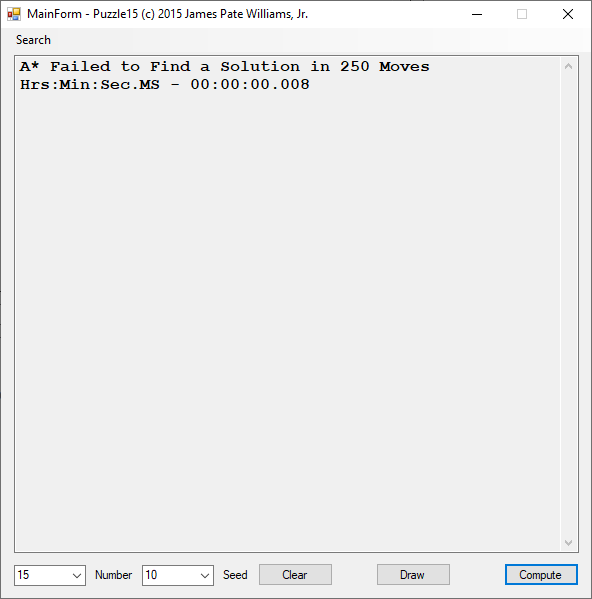
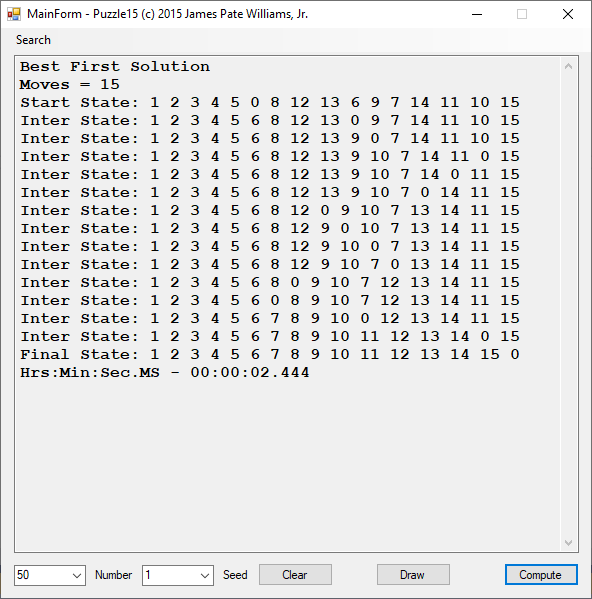
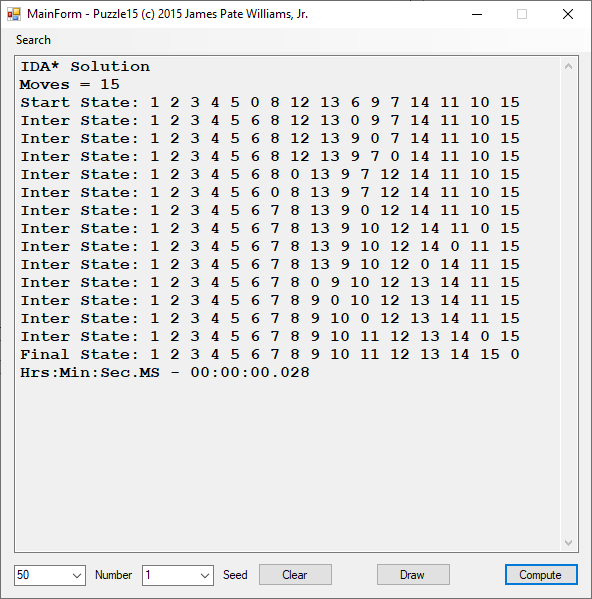
Back in the year 1999 I studied Constraint Satisfaction Problems (CSPs) which is a branch of the computer science discipline artificial intelligence (AI). I took a course in Artificial Intelligence and then a Machine Learning course both under Professor Gerry V. Dozier at Auburn University in the Winter and Spring Quarters of 1999. Professor Dozier was my Master of Software Engineering degree advisor. The N-Queens Problem is a constraint satisfaction problem within the setting of a N-by-N chessboard with the queens arranged such the no queens are attacking any other queens. The N-Queens Problem is believed to be a NP-Complete Problem which means only non-deterministic polynomial time algorithms solve the problem. I bought copies of Foundations of Constraint Satisfaction by E. P. K. Tsang for Professor Dozier and me in 2000. The back-marking algorithm is found in section 5.4.3 page 147 of the textbook. I implemented several algorithms from the textbook. Below is the source code for the back-marking algorithm and single runs from N = 4 to N = 12. A single run is not a statistically significantly experiment. Generally, 30 or more experimental trials are needed for statistical significance.
/*
Author: James Pate Williams, Jr. (c) 2000 - 2023
Backmarking algorithm applied to the N-Queens CSP.
Algorithm from _Foundations of Constraint Satisfaction_
by E. P. K. Tsang section 5.4.3 page 147.
*/
#include <iomanip>
#include <iostream>
#include <stdlib.h>
#include <time.h>
#include <algorithm>
#include <vector>
#include <chrono>
using namespace std::chrono;
using namespace std;
// https://www.geeksforgeeks.org/measure-execution-time-function-cpp/
int constraintsViolated(vector<int>& Q) {
int a, b, c = 0, i, j, n;
n = Q.size();
for (i = 0; i < n; i++) {
a = Q[i];
for (j = 0; j < n; j++) {
b = Q[j];
if (i != j && a != -1 && b != -1) {
if (a == b) c++;
if (i - j == a - b || i - j == b - a) c++;
}
}
}
return c;
}
bool satisfies(int x, int v, int y, int vp) {
if (x == y) return false;
if (v == vp) return false;
if (x - y == v - vp || x - y == vp - v) return false;
return true;
}
bool Compatible(int x, int v, int* LowUnit, int* Ordering, int** Mark,
vector<int> compoundLabel) {
bool compat = true;
int vp, y = LowUnit[x];
while (Ordering[y] < Ordering[x] && compat) {
if (compoundLabel[y] != -1) {
vp = compoundLabel[y];
if (satisfies(x, v, y, vp))
y = Ordering[y] + 1;
else
compat = false;
}
}
Mark[x][v] = Ordering[y];
return compat;
}
bool BM1(int Level, int* LowUnit, int* Ordering, int** Mark,
vector<int> unlabelled, vector<int> compoundLabel, vector<int>& solution) {
bool result;
int i, v, x, y;
vector<int> Dx(compoundLabel.size());
if (unlabelled.empty()) {
for (i = 0; i < (int)compoundLabel.size(); i++)
solution[i] = compoundLabel[i];
return true;
}
for (i = 0; i < (int)unlabelled.size(); i++) {
x = unlabelled[i];
if (Ordering[x] == Level) break;
}
result = false;
for (i = 0; i < (int)compoundLabel.size(); i++)
Dx[i] = i;
do {
// pick a random value from domain of x
i = rand() % Dx.size();
v = Dx[i];
vector<int>::iterator vIterator = find(Dx.begin(), Dx.end(), v);
Dx.erase(vIterator);
if (Mark[x][v] >= LowUnit[x]) {
if (Compatible(x, v, LowUnit, Ordering, Mark, compoundLabel)) {
compoundLabel[x] = v;
vIterator = find(unlabelled.begin(), unlabelled.end(), x);
unlabelled.erase(vIterator);
result = BM1(Level + 1, LowUnit, Ordering, Mark,
unlabelled, compoundLabel, solution);
if (!result) {
compoundLabel[x] = -1;
unlabelled.push_back(x);
}
}
}
} while (!Dx.empty() && !result);
if (!result) {
LowUnit[x] = Level - 1;
for (i = 0; i < (int)unlabelled.size(); i++) {
y = unlabelled[i];
LowUnit[y] = LowUnit[y] < Level - 1 ? LowUnit[y] : Level - 1;
}
}
return result;
}
bool Backmark1(vector<int> unlabelled, vector<int> compoundLabel, vector<int>& solution) {
int i, n = compoundLabel.size(), v, x;
int* LowUnit = new int[n];
int* Ordering = new int[n];
int** Mark = new int* [n];
for (i = 0; i < n; i++)
Mark[i] = new int[n];
i = 0;
for (x = 0; x < n; x++) {
LowUnit[x] = 0;
for (v = 0; v < n; v++)
Mark[x][v] = 0;
Ordering[x] = i++;
}
return BM1(0, LowUnit, Ordering, Mark, unlabelled, compoundLabel, solution);
}
void printSolution(vector<int>& solution) {
char hyphen[256] = { '\0' };
int column, i, i4, n = solution.size(), row;
if (n <= 12) {
for (i = 0; i < n; i++) {
i4 = i * 4;
hyphen[i4 + 0] = '-';
hyphen[i4 + 1] = '-';
hyphen[i4 + 2] = '-';
hyphen[i4 + 3] = '-';
}
i4 = i * 4;
hyphen[i4 + 0] = '-';
hyphen[i4 + 1] = '\n';
hyphen[i4 + 2] = '\0';
for (row = 0; row < n; row++) {
column = solution[row];
cout << hyphen;
for (i = 0; i < column; i++)
cout << "| ";
cout << "| Q ";
for (i = column + 1; i < n; i++)
cout << "| ";
cout << '|' << endl;
}
cout << hyphen;
}
else
for (row = 0; row < n; row++)
cout << row << ' ' << solution[row] << endl;
}
int main(int argc, char* argv[]) {
while (true)
{
int i, n;
cout << "Number of queens (4 - 12) (0 to quit): ";
cin >> n;
if (n == 0)
break;
if (n < 4 || n > 12)
{
cout << "Illegal number of queens" << endl;
continue;
}
auto start = high_resolution_clock::now();
vector<int> compoundLabel(n, -1), solution(n, -1), unlabelled(n);
for (i = 0; i < n; i++)
unlabelled[i] = i;
if (Backmark1(unlabelled, compoundLabel, solution))
printSolution(solution);
else
cout << "problem has no solution" << endl;
auto stop = high_resolution_clock::now();
auto duration = duration_cast<microseconds>(stop - start);
cout << "Runtime: " << setprecision(3) << setw(5)
<< (double)duration.count() / 1.0e3 << " milliseconds" << endl;
}
return 0;
}