Category: C++ Computer Applications

Fast and Slow Matrix Multiplication by James Pate Williams, Jr. © January 13, 2024, All Applicable Rights Reserved

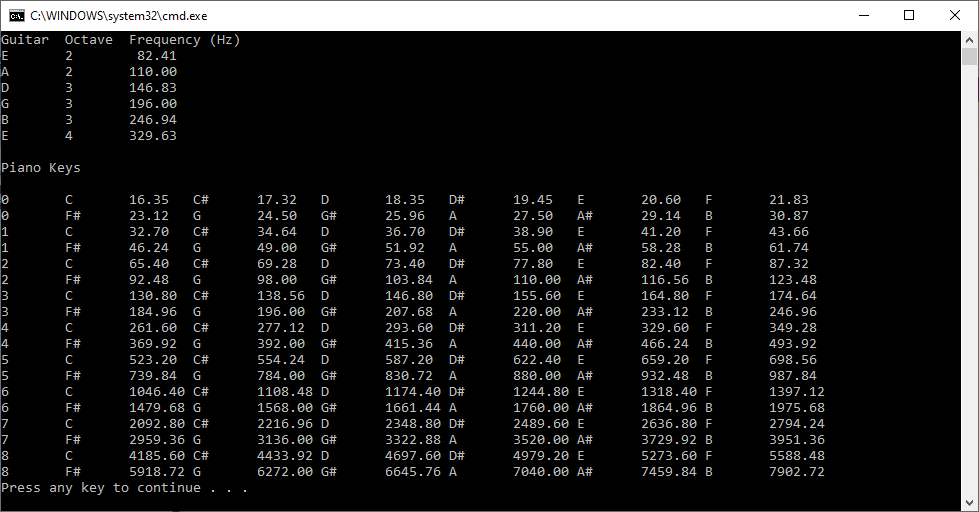
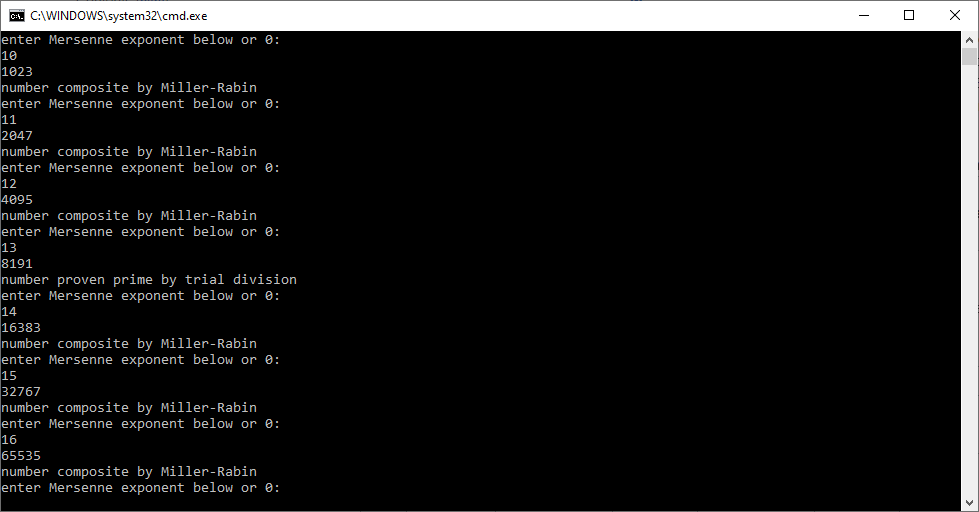
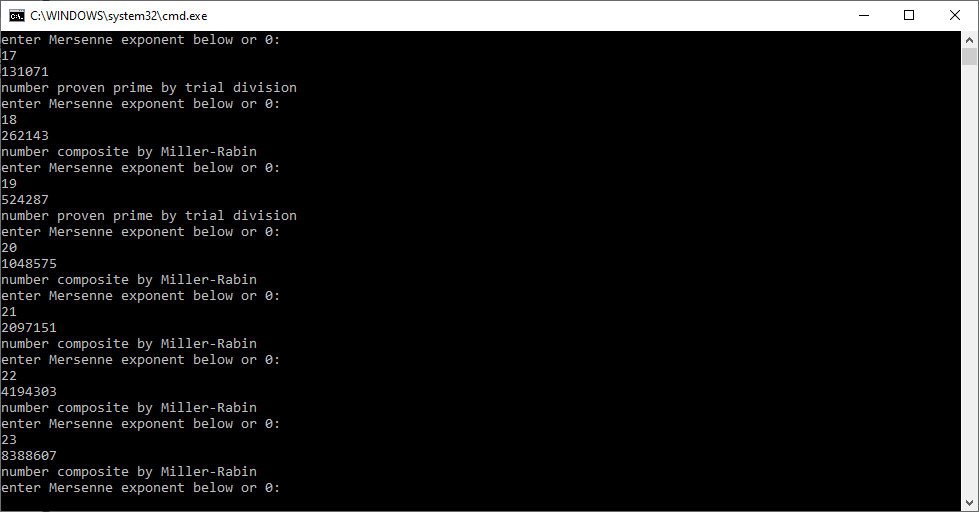
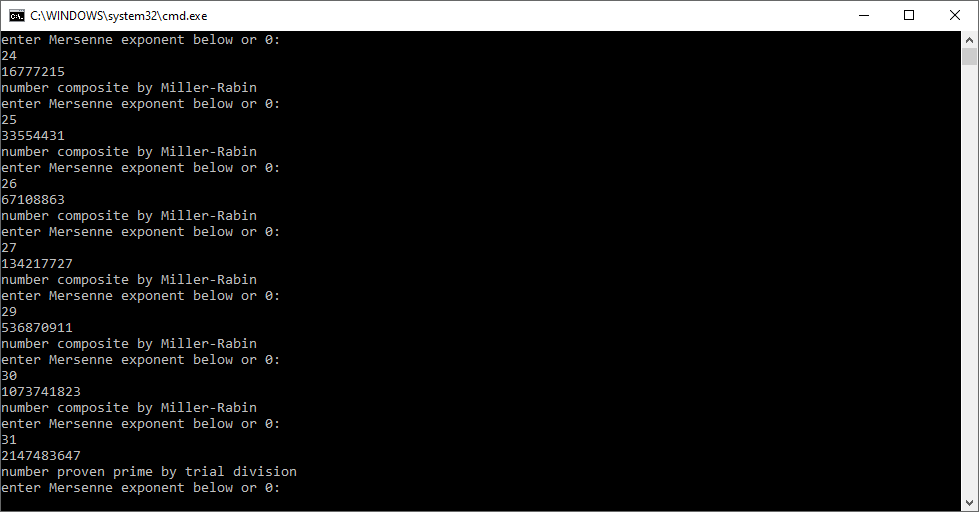
Note: For comparison with a paper on matrix operations, we use column major order also known as column major echelon order. Column major order is used in Fortran and row major order is utilized in C computations.

Click to access Lecture4.pdf

Here is the supposedly slow C source code:

void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;

    for (int j = 1; j <= n; j++)
    {
        for (int i = 1; i <= n; i++)
        {
            double t = 0;

            for (int k = 1; k <= n; k++)
                t += a[i][k] * b[k][j];

            c[i][j] = t;
        }
    }
}

And now we present the allegedly fast multiplication code:

void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;
    
    for (int j = 1; j <= n; j++)
    {
        for (int k = 1; k <= n; k++)
        {
            double t = b[k][j];

            for (int i = 1; i <= n; i++)
                c[i][j] += a[i][k] * t;
        }
    }
}

Finally, we have another algorithm for matrix multiplication:

void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;

    for (int j = 1; j <= n; j++)
    {
        for (int i = 1; i <= n; i++)
        {
            for (int k = 1; k <= n; k++)
                c[i][j] += a[i][k] * b[k][j];
        }
    }
}

We performed the following experiments.



slow runtime in microseconds: 2736

semi runtime in microseconds: 4001

fast runtime in microseconds: 5293

n * n = 10000

equal = 10000

n * n = 10000

equal = 10000

slow runtime in microseconds: 21962

semi runtime in microseconds: 29585

fast runtime in microseconds: 28701

n * n = 40000

equal = 40000

n * n = 40000

equal = 40000

slow runtime in microseconds: 67256

semi runtime in microseconds: 101554

fast runtime in microseconds: 107969

n * n = 90000

equal = 90000

n * n = 90000

equal = 90000

slow runtime in microseconds: 183839

semi runtime in microseconds: 268616

fast runtime in microseconds: 244832

n * n = 160000

equal = 160000

n * n = 160000

equal = 160000

slow runtime in microseconds: 428263

semi runtime in microseconds: 638721

fast runtime in microseconds: 650535

n * n = 250000

equal = 250000

n * n = 250000

equal = 250000



C:\Users\james\source\repos\FastMatrixMultiplication\Debug\FastMatrixMultiplication.exe (process 29552) exited with code 0.

Press any key to close this window . . .































// FastMatrixMultiplication.cpp : This file contains the 'main' function. Program execution begins and ends there.
// https://www-users.york.ac.uk/~mijp1/teaching/grad_HPC_for_MatSci/Lecture4.pdf
// https://stackoverflow.com/questions/25483620/how-to-measure-running-time-of-specific-function-in-c-very-accurate

#include <stdlib.h>
#include <chrono>
#include <iostream>
using namespace std;

typedef chrono::high_resolution_clock Clock;

void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;
    
    for (int j = 1; j <= n; j++)
    {
        for (int k = 1; k <= n; k++)
        {
            double t = b[k][j];

            for (int i = 1; i <= n; i++)
                c[i][j] += a[i][k] * t;
        }
    }
}

void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;

    for (int j = 1; j <= n; j++)
    {
        for (int i = 1; i <= n; i++)
        {
            for (int k = 1; k <= n; k++)
                c[i][j] += a[i][k] * b[k][j];
        }
    }
}

void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
    for (int j = 1; j <= n; j++)
        for (int k = 1; k <= n; k++)
            c[j][k] = 0.0;

    for (int j = 1; j <= n; j++)
    {
        for (int i = 1; i <= n; i++)
        {
            double t = 0;

            for (int k = 1; k <= n; k++)
                t += a[i][k] * b[k][j];

            c[i][j] = t;
        }
    }
}

void GenerateMatrix(double** a, int n, int seed)
{
    srand(seed);

    for (int j = 1; j <= n; j++)
    {
        for (int k = 1; k <= n; k++)
        {
            a[j][k] = (double)rand() / RAND_MAX;
        }
    }
}

int main()
{
    for (int n = 100; n <= 500; n += 100)
    {
        double** a = new double* [n + 1];
        double** b = new double* [n + 1];
        double** c = new double* [n + 1];
        double** d = new double* [n + 1];
        double** e = new double* [n + 1];

        for (int j = 0; j < n + 1; j++)
        {
            a[j] = new double[n + 1];
            b[j] = new double[n + 1];
            c[j] = new double[n + 1];
            d[j] = new double[n + 1];
            e[j] = new double[n + 1];
        }

        GenerateMatrix(a, n, 1);
        GenerateMatrix(b, n, 2);

        auto clock1 = Clock::now();
        ColMajorSlowMatMul(a, b, c, n);
        auto clock2 = Clock::now();
        long long microseconds1 = chrono::duration_cast<chrono::microseconds>
            (clock2 - clock1).count();
    
        auto clock3 = Clock::now();
        ColMajorSemiMatMul(a, b, d, n);
        auto clock4 = Clock::now();
        long long microseconds2 = chrono::duration_cast<chrono::microseconds>
            (clock4 - clock3).count();

        auto clock5 = Clock::now();
        ColMajorFastMatMul(a, b, e, n);
        auto clock6 = Clock::now();
        long long microseconds3 = chrono::duration_cast<chrono::microseconds>
            (clock6 - clock5).count();

        cout << "slow runtime in microseconds: " << microseconds1 << endl;
        cout << "semi runtime in microseconds: " << microseconds2 << endl;
        cout << "fast runtime in microseconds: " << microseconds3 << endl;

        long long equal = 0;

        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                if (c[j][k] == d[j][k])
                    equal++;

        cout << "n * n = " << n * n << endl;
        cout << "equal = " << equal << endl;

        equal = 0;

        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                if (c[j][k] == e[j][k])
                    equal++;

        cout << "n * n = " << n * n << endl;
        cout << "equal = " << equal << endl;

        for (int j = 0; j < n + 1; j++)
        {
            delete[] a[j];
            delete[] b[j];
            delete[] c[j];
            delete[] d[j];
            delete[] e[j];
        }

        delete[] a;
        delete[] b;
        delete[] c;
        delete[] d;
        delete[] e;
    }
}

Some Helium Coulomb Integrals over Six Dimensions by James Pate Williams, Jr. Source Code in C++ Development over December 15 – 16, 2023

some-helium-coulomb-integrals-1Download

Revised Translated Source Code from May 15, 2015, by James Pate Williams, Jr.

revisited-with-source-code-translation-and-revisionDownload

New and Corrected Ground State Energy Numerical Computation for the Helium Like Atom (Atomic Number 2) by James Pate Williams, Jr.

approximate-solution-of-the-schrodinger-equation-for-the-helium-atom-1Download
new-variational-treatment-of-the-helium-like-atom-revisedDownload

A New Calculus of Variations Solution of the Schrödinger Equation for the Lithium Like Atom’s Ground State Energy

This computation took a lot longer time to reach a much better solution than my previously published result.

new-variational-solution-for-the-lithiumDownload

A Calculus of Variations Solution to the Quantum Mechanical Schrödinger Wave Equation for the Lithium Like Atom (Atomic Number Z = 3) by James Pate Williams, Jr.

variational-solution-for-the-lithiumDownload

Guitar String and Piano Key Frequencies by James Pate Williams, Jr.

// FrequencyKey.cpp : Defines the entry point for the console application.
// James Pate Willims, Jr. (c) All Applicable Rights Reserved

#include "stdafx.h"
#include <math.h>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
using namespace std;

vector<string> pnote;
double a = pow(2.0, 1.0 / 12.0);
double f0 = 440.0, gStrF[6];
double e2, a2, d3, g3, b3, e4;
double pfreq[9 * 12];
int offset = 0;

double fn(int n)
{
	return f0 * pow(a, n);
}

void printFrequency(char note, int octave, double frequency)
{
	cout << note << "\t" << octave << "\t";
	cout << setw(6) << fixed << setprecision(2);
	cout << frequency << endl;
}

int main()
{
	for (int octave = 0; octave <= 8; octave++)
	{
		pnote.push_back("C");
		pnote.push_back("C#");
		pnote.push_back("D");
		pnote.push_back("D#");
		pnote.push_back("E");
		pnote.push_back("F");
		pnote.push_back("F#");
		pnote.push_back("G");
		pnote.push_back("G#");
		pnote.push_back("A");
		pnote.push_back("A#");
		pnote.push_back("B");
	}

	pfreq[0] = 16.35;
	pfreq[1] = 17.32;
	pfreq[2] = 18.35;
	pfreq[3] = 19.45;
	pfreq[4] = 20.6;
	pfreq[5] = 21.83;
	pfreq[6] = 23.12;
	pfreq[7] = 24.5;
	pfreq[8] = 25.96;
	pfreq[9] = 27.5;
	pfreq[10] = 29.14;
	pfreq[11] = 30.87;
	
	for (int octave = 1; octave <= 8; octave++)
	{
		for (int i = 0; i < 12; i++)
		{
			pfreq[octave * 12 + i] = 2.0 * pfreq[(octave - 1) * 12 + i];
		}
	}

	gStrF[0] = e2 = fn(offset - 29);
	gStrF[1] = a2 = fn(offset - 24);
	gStrF[2] = d3 = fn(offset - 19);
	gStrF[3] = g3 = fn(offset - 14);
	gStrF[4] = b3 = fn(offset - 10);
	gStrF[5] = e4 = fn(offset - 5);

	cout << "Guitar\tOctave\tFrequency (Hz)" << endl;
	
	printFrequency('E', 2, e2);
	printFrequency('A', 2, a2);
	printFrequency('D', 3, d3);
	printFrequency('G', 3, g3);
	printFrequency('B', 3, b3);
	printFrequency('E', 4, e4);
	
	cout << endl;
	cout << "Piano Keys" << endl << endl;

	for (int octave = 0; octave <= 8; octave++)
	{
		for (int i = 0; i < 2; i++)
		{
			cout << octave << '\t';

			for (int j = 0; j < 6; j++)
			{
				{
					cout << pnote[(12 * octave + 6 * i + j) % 12] << '\t';
					cout << pfreq[(12 * octave + 6 * i + j)] << '\t';
				}
			}

			cout << endl;
		}
	}

	return 0;
}

https://en.wikipedia.org/wiki/Piano_key_frequencies#:~:text=%20Every%20octave%20is%20made%20of%20twelve%20steps,Hz%20and%20the%20sixth%20A%20is%20880%20Hz%29.