C++ Computer Applications – Page 21 – Numerical Explorations

Computation of Ulam Primes in C++ Translation from Python by James Pate Williams, Jr (c) 2008 – 2023.

http://en.wikipedia.org/wiki/Ulam_numbers

Stanislaw Marcin Ulam worked on the Manhattan Project by an invitation from John von Neumann:

https://en.wikipedia.org/wiki/Stanis%C5%82aw_Ulam#Move_to_the_United_States

Ulam is given credit for the Teller-Ulam design of the hydrogen bomb. Edward Teller was one of the first proponent of human induced global climate change:

https://en.wikipedia.org/wiki/Edward_Teller#Hydrogen_bomb

/*
	Translator: James Pate Williams, Jr. (c) 2008

	Translated to C++ from the following python code:

	http://en.wikipedia.org/wiki/Ulam_numbers
	https://oeis.org/A002858

	ulam_i = [1,2,3]
	ulam_j = [1,2,3]
	for cand in range(4,5000):
		res = []
		for i in ulam_i:
			for j in ulam_j:
				if i == j or j > i: pass
				else:
					res.append(i+j)
				if res.count(cand) == 1:
				ulam_i.append(cand)
				ulam_j.append(cand)
			print ulam_i

	Find the Ulam primes <= 5000
*/

#include "stdafx.h"
#include <time.h>
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;

bool sieve[10000000];

void PopulateSieve(bool *sieve, int number) {

	// sieve of Eratosthenes

	int c, inc, i, n = number - 1;

	for (i = 0; i < n; i++)
		sieve[i] = false;

	sieve[1] = false;
	sieve[2] = true;

	for (i = 3; i <= n; i++)
		sieve[i] = (i & 1) == 1 ? true : false;

	c = 3;

	do {
		i = c * c;
		inc = c + c;

		while (i <= n) {
			sieve[i] = false;
			i += inc;
		}

		c += 2;
		while (!sieve[c])
			c++;
	} while (c * c <= n);
}

bool CountEqualOne(int number, vector<int> ulam) {
	int count = 0, i;

	for (i = 0; i < ulam.size(); i++)
		if (ulam[i] == number)
			count++;

	return count == 1;
}

void UlamNumbers(int n) {
	int candidate, i, j;
	vector<int> vI;
	vector<int> vJ;
	vector<int> UlamResult;

	PopulateSieve(sieve, 10000000);

	for (i = 1; i <= 3; i++) {
		vI.push_back(i);
		vJ.push_back(i);
	}

	for (candidate = 4; candidate <= n; candidate++) {

		UlamResult.clear();

		for (i = 0; i < vI.size(); i++) {
			int ui = vI[i];

			for (j = 0; j < vJ.size(); j++) {
				int uj = vJ[j];

				if (ui == uj || uj > ui)
					continue;

				UlamResult.push_back(ui + uj);
			}
		}

		if (CountEqualOne(candidate, UlamResult)) {
			vI.push_back(candidate);
			vJ.push_back(candidate);
		}
	}

	j = 0;

	for (i = 0; i < vI.size(); i++) {
		if (sieve[vI[i]]) {
			cout << setw(4) << vI[i] << ' ';

			if ((j + 1) % 10 == 0) {
				j = 0;
				cout << endl;
			}
			else
				j++;
		}
	}

	cout << endl;
}

int main(int argc, char * const argv[]) {
	clock_t clock0 = clock();

	cout << "Ulam sequence prime numbers < 5000" << endl << endl;
	UlamNumbers(5000);
	clock0 = clock() - clock0;
	cout << endl << endl << "seconds = ";
	cout << (double)clock0 / CLOCKS_PER_SEC << endl;
	return 0;
}

Blast from the Past 1997 Image of a Matrix by James Pate Williams, Jr.

/*
  Author:  Pate Williams (c) 1997

  "Algorithm 2.3.2 (Image of a Matrix). Given an
  m by n matrix M = (m[i][i]) with 1 <= i <= m and
  1 <= j <= n having coefficients in the field K,
  this algorithm outputs a basis of the image of
  M, i. e. vector space spanned by the columns of
  M." -Henri Cohen- See "A Course in Computational
  Algebraic Number Theory" by Henri Cohen pages
  58-59. We specialize the code to the field Zp.
*/

#include <stdio.h>
#include <stdlib.h>

long** create_matrix(long m, long n)
{
    long i, ** matrix = (long**)calloc(m, sizeof(long*));

    if (!matrix) {
        fprintf(stderr, "fatal error\ninsufficient memory\n");
        fprintf(stderr, "from create_matrix\n");
        exit(1);
    }
    for (i = 0; i < m; i++) {
        matrix[i] = (long*)calloc(n, sizeof(long));
        if (!matrix[i]) {
            fprintf(stderr, "fatal error\ninsufficient memory\n");
            fprintf(stderr, "from create_matrix\n");
            exit(1);
        }
    }
    return matrix;
}

void delete_matrix(long m, long** matrix)
{
    long i;

    for (i = 0; i < m; i++) free(matrix[i]);
    free(matrix);
}

void Euclid_extended(long a, long b, long* u,
    long* v, long* d)
{
    long q, t1, t3, v1, v3;

    *u = 1, * d = a;
    if (b == 0) {
        *v = 0;
        return;
    }
    v1 = 0, v3 = b;
#ifdef DEBUG
    printf("----------------------------------\n");
    printf(" q    t3   *u   *d   t1   v1   v3\n");
    printf("----------------------------------\n");
#endif
    while (v3 != 0) {
        q = *d / v3;
        t3 = *d - q * v3;
        t1 = *u - q * v1;
        *u = v1, * d = v3;
#ifdef DEBUG
        printf("%4ld %4ld %4ld ", q, t3, *u);
        printf("%4ld %4ld %4ld %4ld\n", *d, t1, v1, v3);
#endif
        v1 = t1, v3 = t3;
    }
    *v = (*d - a * *u) / b;
#ifdef DEBUG
    printf("----------------------------------\n");
#endif
}

long inv(long number, long modulus)
{
    long d, u, v;

    Euclid_extended(number, modulus, &u, &v, &d);
    if (d == 1) return u;
    return 0;
}

void image(long m, long n, long p,
    long** M, long** X, long* r)
{
    int found;
    long D, i, j, k, s;
    long* c = (long*)calloc(m, sizeof(long));
    long* d = (long*)calloc(n, sizeof(long));
    long** N = create_matrix(m, n);

    if (!c || !d) {
        fprintf(stderr, "fatal error\ninsufficient memory\n");
        fprintf(stderr, "from kernel\n");
        exit(1);
    }
    for (i = 0; i < m; i++) {
        c[i] = -1;
        for (j = 0; j < n; j++) N[i][j] = M[i][j];
    }
    *r = 0;
    for (k = 0; k < n; k++) {
        found = 0, j = 0;
        while (!found && j < m) {
            found = M[j][k] != 0 && c[j] == -1;
            if (!found) j++;
        }
        if (found) {
            D = p - inv(M[j][k], p);
            M[j][k] = p - 1;
            for (s = k + 1; s < n; s++)
                M[j][s] = (D * M[j][s]) % p;
            for (i = 0; i < m; i++) {
                if (i != j) {
                    D = M[i][k];
                    M[i][k] = 0;
                    for (s = k + 1; s < n; s++) {
                        M[i][s] = (M[i][s] + D * M[j][s]) % p;
                        if (M[i][s] < 0) M[i][s] += p;
                    }
                }
            }
            c[j] = k;
            d[k] = j;
        }
        else {
            *r = *r + 1;
            d[k] = -1;
        }
    }
    for (j = 0; j < m; j++) {
        if (c[j] != -1) {
            for (i = 0; i < n; i++) {
                if (i < m) X[i][j] = N[i][c[j]];
                else X[i][j] = 0;
            }
        }
    }
    delete_matrix(m, N);
    free(c);
    free(d);
}

void print_matrix(long m, long n, long** a)
{
    long i, j;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++)
            printf("%2ld ", a[i][j]);
        printf("\n");
    }
}

int main(void)
{
    long i, j, m = 8, n = 8, p = 13, r;
    long a[8][8] = { {0,  0,  0,  0,  0,  0,  0,  0},
                    {2,  0,  7, 11, 10, 12,  5, 11},
                    {3,  6,  3,  3,  0,  4,  7,  2},
                    {4,  3,  6,  4,  1,  6,  2,  3},
                    {2, 11,  8,  8,  2,  1,  3, 11},
                    {6, 11,  8,  6,  2,  6, 10,  9},
                    {5, 11,  7, 10,  0, 11,  6, 12},
                    {3,  3, 12,  5,  0, 11,  9, 11} };
    long** M = create_matrix(m, n);
    long** X = create_matrix(n, n);

    for (i = 0; i < m; i++)
        for (j = 0; j < n; j++)
            M[i][j] = a[j][i];
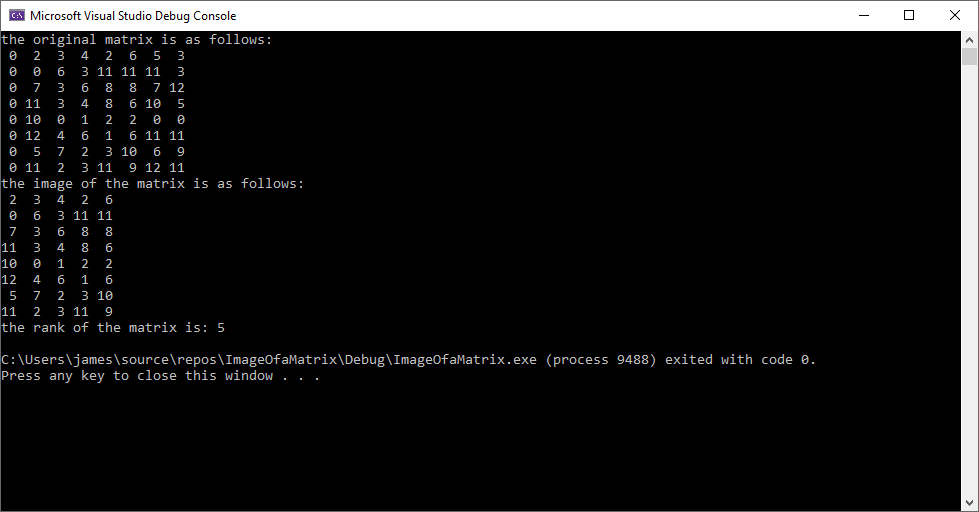
    printf("the original matrix is as follows:\n");
    print_matrix(m, n, M);
    image(m, n, p, M, X, &r);
    printf("the image of the matrix is as follows:\n");
    print_matrix(n, n - r, X);
    printf("the rank of the matrix is: %ld\n", n - r);
    delete_matrix(m, M);
    delete_matrix(n, X);
    return 0;
}

First Blast from the Past (1997) Computing the Inverse Image of a Matrix by James Pate Williams, Jr.

/*
  Author:  Pate Williams (c) 1997

  "Algorithm 2.3.5 (Inverse Image Matrix). Let M be
  an m by n matrix and V be an m by r matrix, where
  n <= m. This algorithm either outputs a message
  saying that some column vector of V is not in the
  image of M, or outputs an n by r matrix X such
  that V = MX." -Henri Cohen- See "A Course in Com-
  putational Algebraic Number Theory" by Henri
  Cohen pages 60-61. We specialize to the field Q.
*/

#include <stdio.h>
#include <stdlib.h>

double** create_matrix(long m, long n)
{
    double** matrix = (double**)calloc(m, sizeof(double*));
    long i;

    if (!matrix) {
        fprintf(stderr, "fatal error\ninsufficient memory\n");
        fprintf(stderr, "from create_matrix\n");
        exit(1);
    }
    for (i = 0; i < m; i++) {
        matrix[i] = (double*)calloc(n, sizeof(double));
        if (!matrix[i]) {
            fprintf(stderr, "fatal error\ninsufficient memory\n");
            fprintf(stderr, "from create_matrix\n");
            exit(1);
        }
    }
    return matrix;
}

void delete_matrix(long m, double** matrix)
{
    long i;

    for (i = 0; i < m; i++) free(matrix[i]);
    free(matrix);
}

void inverse_image_matrix(long m, long n, long r,
    double** M, double** V,
    double** X)
{
    double ck, d, sum, t;
    double** B = create_matrix(m, r);
    int found;
    long i, j, k, l;

    for (i = 0; i < m; i++)
        for (j = 0; j < r; j++)
            B[i][j] = V[i][j];
    for (j = 0; j < n; j++) {
        found = 0, i = j;
        while (!found && i < m) {
            found = M[i][j] != 0;
            if (!found) i++;
        }
        if (!found) {
            fprintf(stderr, "fatal error\nnot linearly independent\n");
            fprintf(stderr, "from inverse_image_matrix\n");
            exit(1);
        }
        if (i > j) {
            for (l = 0; l < n; l++)
                t = M[i][l], M[i][l] = M[j][l], M[j][l] = t;
            for (l = 0; l < r; l++)
                t = B[i][l], B[i][l] = B[j][l], B[j][l] = t;
        }
        d = 1.0 / M[j][j];
        for (k = j + 1; k < m; k++) {
            ck = d * M[k][j];
            for (l = j + 1; l < n; l++)
                M[k][l] -= ck * M[j][l];
            for (l = 0; l < r; l++)
                B[k][l] -= ck * B[j][l];
        }
    }
    for (i = n - 1; i >= 0; i--) {
        for (k = 0; k < r; k++) {
            sum = 0;
            for (j = i + 1; j < n; j++)
                sum += M[i][j] * X[j][k];
            X[i][k] = (B[i][k] - sum) / M[i][i];
        }
    }
    for (k = n + 1; k < m; k++) {
        for (j = 0; j < r; j++) {
            sum = 0;
            for (i = 0; i < n; i++)
                sum += M[k][i] * X[i][j];
            if (sum != B[k][j]) {
                fprintf(stderr, "fatal error\ncolumn not in image\n");
                fprintf(stderr, "from inverse_image_matrix\n");
                exit(1);
            }
        }
    }
    delete_matrix(m, B);
}

void matrix_multiply(long m, long n, long r,
    double** a, double** b,
    double** c)
    /* c = a * b */
{
    double sum;
    long i, j, k;

    for (i = 0; i < m; i++) {
        for (j = 0; j < r; j++) {
            sum = 0.0;
            for (k = 0; k < n; k++)
                sum += a[i][k] * b[k][j];
            c[i][j] = sum;
        }
    }
}

void print_matrix(long m, long n, double** a)
{
    long i, j;

    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++)
            printf("%+10.6lf ", a[i][j]);
        printf("\n");
    }
}

int main(void)
{
    long i, j, m = 4, n = 4, r = 4;
    double** c = create_matrix(m, n);
    double** M = create_matrix(m, n);
    double** V = create_matrix(m, r);
    double** X = create_matrix(n, r);

    for (i = 0; i < m; i++) {
        c[i][i] = M[i][i] = 2.0;
        if (i > 0)
            c[i][i - 1] = M[i][i - 1] = -1.0;
        if (i < m - 1)
            c[i][i + 1] = M[i][i + 1] = -1.0;
    }
    for (i = 0; i < m; i++)
        for (j = 0; j < r; j++)
            V[i][j] = i + j + 1;
    printf("M is as follows:\n");
    print_matrix(m, n, M);
    printf("V is as follows:\n");
    print_matrix(m, r, V);
    inverse_image_matrix(m, n, r, M, V, X);
    printf("X is as follows:\n");
    print_matrix(n, r, X);
    matrix_multiply(m, n, r, c, X, M);
    printf("MX is as follows:\n");
    print_matrix(m, r, M);
    delete_matrix(m, c);
    delete_matrix(m, M);
    delete_matrix(m, V);
    delete_matrix(n, X);
    return 0;
}

Back-marking Algorithm for the N-Queens Problem

Back in the year 1999 I studied Constraint Satisfaction Problems (CSPs) which is a branch of the computer science discipline artificial intelligence (AI). I took a course in Artificial Intelligence and then a Machine Learning course both under Professor Gerry V. Dozier at Auburn University in the Winter and Spring Quarters of 1999. Professor Dozier was my Master of Software Engineering degree advisor. The N-Queens Problem is a constraint satisfaction problem within the setting of a N-by-N chessboard with the queens arranged such the no queens are attacking any other queens. The N-Queens Problem is believed to be a NP-Complete Problem which means only non-deterministic polynomial time algorithms solve the problem. I bought copies of Foundations of Constraint Satisfaction by E. P. K. Tsang for Professor Dozier and me in 2000. The back-marking algorithm is found in section 5.4.3 page 147 of the textbook. I implemented several algorithms from the textbook. Below is the source code for the back-marking algorithm and single runs from N = 4 to N = 12. A single run is not a statistically significantly experiment. Generally, 30 or more experimental trials are needed for statistical significance.

/*
	Author:	James Pate Williams, Jr. (c) 2000 - 2023

	Backmarking algorithm applied to the N-Queens CSP.
	Algorithm from _Foundations of Constraint Satisfaction_
	by E. P. K. Tsang section 5.4.3 page 147.
*/

#include <iomanip>
#include <iostream>
#include <stdlib.h>
#include <time.h>
#include <algorithm>
#include <vector>
#include <chrono>
using namespace std::chrono;
using namespace std;

// https://www.geeksforgeeks.org/measure-execution-time-function-cpp/

int constraintsViolated(vector<int>& Q) {
	int a, b, c = 0, i, j, n;

	n = Q.size();
	for (i = 0; i < n; i++) {
		a = Q[i];
		for (j = 0; j < n; j++) {
			b = Q[j];
			if (i != j && a != -1 && b != -1) {
				if (a == b) c++;
				if (i - j == a - b || i - j == b - a) c++;
			}
		}
	}
	return c;
}

bool satisfies(int x, int v, int y, int vp) {
	if (x == y) return false;
	if (v == vp) return false;
	if (x - y == v - vp || x - y == vp - v) return false;
	return true;
}

bool Compatible(int x, int v, int* LowUnit, int* Ordering, int** Mark,
	vector<int> compoundLabel) {
	bool compat = true;
	int vp, y = LowUnit[x];

	while (Ordering[y] < Ordering[x] && compat) {
		if (compoundLabel[y] != -1) {
			vp = compoundLabel[y];
			if (satisfies(x, v, y, vp))
				y = Ordering[y] + 1;
			else
				compat = false;
		}
	}
	Mark[x][v] = Ordering[y];
	return compat;
}

bool BM1(int Level, int* LowUnit, int* Ordering, int** Mark,
	vector<int> unlabelled, vector<int> compoundLabel, vector<int>& solution) {
	bool result;
	int i, v, x, y;
	vector<int> Dx(compoundLabel.size());

	if (unlabelled.empty()) {
		for (i = 0; i < (int)compoundLabel.size(); i++)
			solution[i] = compoundLabel[i];
		return true;
	}
	for (i = 0; i < (int)unlabelled.size(); i++) {
		x = unlabelled[i];
		if (Ordering[x] == Level) break;
	}
	result = false;
	for (i = 0; i < (int)compoundLabel.size(); i++)
		Dx[i] = i;
	do {
		// pick a random value from domain of x
		i = rand() % Dx.size();
		v = Dx[i];
		vector<int>::iterator vIterator = find(Dx.begin(), Dx.end(), v);
		Dx.erase(vIterator);
		if (Mark[x][v] >= LowUnit[x]) {
			if (Compatible(x, v, LowUnit, Ordering, Mark, compoundLabel)) {
				compoundLabel[x] = v;
				vIterator = find(unlabelled.begin(), unlabelled.end(), x);
				unlabelled.erase(vIterator);
				result = BM1(Level + 1, LowUnit, Ordering, Mark,
					unlabelled, compoundLabel, solution);
				if (!result) {
					compoundLabel[x] = -1;
					unlabelled.push_back(x);
				}
			}
		}
	} while (!Dx.empty() && !result);
	if (!result) {
		LowUnit[x] = Level - 1;
		for (i = 0; i < (int)unlabelled.size(); i++) {
			y = unlabelled[i];
			LowUnit[y] = LowUnit[y] < Level - 1 ? LowUnit[y] : Level - 1;
		}
	}
	return result;
}

bool Backmark1(vector<int> unlabelled, vector<int> compoundLabel, vector<int>& solution) {
	int i, n = compoundLabel.size(), v, x;
	int* LowUnit = new int[n];
	int* Ordering = new int[n];
	int** Mark = new int* [n];

	for (i = 0; i < n; i++)
		Mark[i] = new int[n];
	i = 0;
	for (x = 0; x < n; x++) {
		LowUnit[x] = 0;
		for (v = 0; v < n; v++)
			Mark[x][v] = 0;
		Ordering[x] = i++;
	}
	return BM1(0, LowUnit, Ordering, Mark, unlabelled, compoundLabel, solution);
}

void printSolution(vector<int>& solution) {
	char hyphen[256] = { '\0' };
	int column, i, i4, n = solution.size(), row;

	if (n <= 12) {
		for (i = 0; i < n; i++) {
			i4 = i * 4;
			hyphen[i4 + 0] = '-';
			hyphen[i4 + 1] = '-';
			hyphen[i4 + 2] = '-';
			hyphen[i4 + 3] = '-';
		}
		i4 = i * 4;
		hyphen[i4 + 0] = '-';
		hyphen[i4 + 1] = '\n';
		hyphen[i4 + 2] = '\0';
		for (row = 0; row < n; row++) {
			column = solution[row];
			cout << hyphen;
			for (i = 0; i < column; i++)
				cout << "|   ";
			cout << "| Q ";
			for (i = column + 1; i < n; i++)
				cout << "|   ";
			cout << '|' << endl;
		}
		cout << hyphen;
	}
	else
		for (row = 0; row < n; row++)
			cout << row << ' ' << solution[row] << endl;
}

int main(int argc, char* argv[]) {
	while (true)
	{
		int i, n;
		cout << "Number of queens (4 - 12) (0 to quit): ";
		cin >> n;
		if (n == 0)
			break;
		if (n < 4 || n > 12)
		{
			cout << "Illegal number of queens" << endl;
			continue;
		}
		auto start = high_resolution_clock::now();
		vector<int> compoundLabel(n, -1), solution(n, -1), unlabelled(n);
		for (i = 0; i < n; i++)
			unlabelled[i] = i;
		if (Backmark1(unlabelled, compoundLabel, solution))
			printSolution(solution);
		else
			cout << "problem has no solution" << endl;
		auto stop = high_resolution_clock::now();
		auto duration = duration_cast<microseconds>(stop - start);
		cout << "Runtime: " << setprecision(3) << setw(5)
			<< (double)duration.count() / 1.0e3 << " milliseconds" << endl;
	}
	return 0;
}

Multiple Precision Arithmetic in C++ Implemented by James Pate Williams, Jr.

I have developed a long integer package in C++ using H. T. Lau’s “A Numerical Library in C for Scientists and Engineers”. That library is based on the NUMAL Numerical Algorithms in Algol library. I use 32-bit integers (long) as the basis of the LongInteger type. The base (radix) is 10000 which is the largest base using 32-bit integers. As a test of the library, I use Pollard’s original rho factorization method. I utilized the Alfred J. Menezes et al “Handbook of Applied Cryptography” Miller-Rabin algorithm and ANSI X9.17 pseudo random number generator with Triple-DES as the encryption algorithm. I translated Hans Riesel Pascal code for Euclid’s algorithm and the power modulus technique. I don’t use dynamic long integers a la Hans Riesel’s Pascal multiple precision library. The single precision is 32 32-bit longs and multiple precision 64 32-bit longs.

Here is a typical factorization:

Number to be factored, N = 3 1234 5678 9012
Factor = 3
Is Factor prime? 1
Factor = 4
Is Factor prime? 0
Factor = 102 8806 5751
Is Factor prime? 1
Function Evaluations = 6
Number to be factored, N = 0

The first number of N is the number of base 10000 digits. I verified that 10288065751 was prime using Miller-Rabin and the table found online below:

http://compoasso.free.fr/primelistweb/page/prime/liste_online_en.php

C++ Linear Algebra Package Extension Implemented by James Pate Williams, Jr.

Input file:

The dimensions of the linear system of equations (m and n, m = n):
2
2
The matrix of the linear system of equations (n by n):
1	1
1	2
The right-hand side of the linear system of equations (n by 1):
7	11
The dimensions of the linear system of equations (m and n, m = 2):
2
2
The matrix of the linear system of equations (n by n):
1	1
1	3
The right-hand side of the linear system of equations (n by 1):
7	11
The dimensions of the linear system of equations (m and n, m = n):
2
2
The matrix of the linear system of equations (n by n):
6	3
4	8
The right-hand side of the linear system of equations (n by 1):
5	6
The dimensions of the linear system of equations (m and n, m = n):
2
2
The matrix of the linear system of equations (n by n):
5	3
10	4
The right-hand side of the linear system of equations (n by 1):
8	6
The dimensions of the linear system of equations (m and n, m = n):
3
3
The matrix of the linear system of equations (n by n):
2	1	-1
-3	-1	2
-2	1	2
The right-hand side of the linear system of equations (n by 1):
8	-11	-3

Output file:

The 1st solution of the linear system of equations:
       3	       4	
The 2nd solution of the linear system of equations:
       3	       4	
The determinant of the linear system of equations:
1
The inverse of the linear system of equations:
       2	      -1	
      -1	       1	
The adjoint of the linear system of equations:
       2	      -0	
      -0	       2	
The characteristic polynomial of the linear system of equations:
       1	       2	
The image of the matrix: 
       1	      -1	
       1	       2	
Rank = 2
The 1st solution of the linear system of equations:
       5	       2	
The 2nd solution of the linear system of equations:
       5	       2	
The determinant of the linear system of equations:
2
The inverse of the linear system of equations:
     1.5	    -0.5	
    -0.5	     0.5	
The adjoint of the linear system of equations:
       3	      -0	
      -0	       3	
The characteristic polynomial of the linear system of equations:
       1	       3	
The image of the matrix: 
       1	      -1	
       1	       3	
Rank = 2
The 1st solution of the linear system of equations:
 0.61111	 0.44444	
The 2nd solution of the linear system of equations:
 0.61111	 0.44444	
The determinant of the linear system of equations:
36
The inverse of the linear system of equations:
 0.22222	-0.11111	
-0.083333	 0.16667	
The adjoint of the linear system of equations:
      48	      -0	
      -0	      48	
The characteristic polynomial of the linear system of equations:
       1	      48	
The image of the matrix: 
       6	      -1	
       4	       8	
Rank = 2
The 1st solution of the linear system of equations:
    -1.4	       5	
The 2nd solution of the linear system of equations:
    -1.4	       5	
The determinant of the linear system of equations:
-10
The inverse of the linear system of equations:
    -0.4	       1	
     0.3	    -0.5	
The adjoint of the linear system of equations:
      20	      -0	
      -0	      20	
The characteristic polynomial of the linear system of equations:
       1	      20	
The image of the matrix: 
       5	      -1	
      10	       4	
Rank = 2
The 1st solution of the linear system of equations:
       2	       3	      -1	
The 2nd solution of the linear system of equations:
       2	       3	      -1	
The determinant of the linear system of equations:
1
The inverse of the linear system of equations:
       4	       5	      -2	
       3	       4	      -2	
      -1	      -1	       1	
The adjoint of the linear system of equations:
      -4	       0	       0	
       0	      -4	       0	
       0	       0	      -4	
The characteristic polynomial of the linear system of equations:
       1	      -7	       4	
The image of the matrix: 
       2	      -1	       2	
      -3	       0	      -1	
      -2	       0	       4	
Rank = 3

// Algorithms from "A Course in Computational
// Algebraic Number Theory" by Henri Cohen
// Implemented by James Pate Williams, Jr.
// Copyright (c) 2023 All Rights Reserved

#pragma once
#include "pch.h"

template<class T> class Matrix
{
public:
	size_t m, n;
	T** data;

	Matrix() { m = 0; n = 0; data = NULL; };
	Matrix(size_t m, size_t n)
	{
		this->m = m;
		this->n = n;
		data = new T*[m];

		if (data == NULL)
			exit(-300);

		for (size_t i = 0; i < m; i++)
		{
			data[i] = new T[n];

			if (data[i] == NULL)
				exit(-301);
		}
	};
	void OutputMatrix(
		fstream& outs, char fill, int precision, int width)
	{
		for (size_t i = 0; i < m; i++)
		{
			for (size_t j = 0; j < n; j++)
			{
				outs << setfill(fill) << setprecision(precision);
				outs << setw(width) << data[i][j] << '\t';
			}

			outs << endl;
		}
	};
};

template<class T> class Vector
{
public:
	size_t n;
	T* data;

	Vector() { n = 0; data = NULL; };
	Vector(size_t n)
	{
		this->n = n;
		data = new T[n];
	};
	void OutputVector(
		fstream& outs, char fill, int precision, int width)
	{
		for (size_t i = 0; i < n; i++)
		{
			outs << setfill(fill) << setprecision(precision);
			outs << setw(width) << data[i] << '\t';
		}

		outs << endl;
	};
};

class LinearAlgebra
{
public:
	bool initialized;
	size_t m, n;
	Matrix<double> M;
	Vector<double> B;

	LinearAlgebra()
	{ 
		initialized = false;
		m = 0; n = 0;
		M.data = NULL;
		B.data = NULL;
	};
	LinearAlgebra(size_t m, size_t n)
	{
		initialized = false;
		this->m = m;
		this->n = n;
		this->M.m = m;
		this->M.n = n;
		this->B.n = n;
		this->M.data = new double*[m];
		this->B.data = new double[n];

		if (M.data != NULL)
		{
			for (size_t i = 0; i < m; i++)
			{
				this->M.data[i] = new double[n];

				for (size_t j = 0; j < n; j++)
					this->M.data[i][j] = 0;
			}
		}

		if (B.data != NULL)
		{
			this->B.data = new double[n];

			for (size_t i = 0; i < n; i++)
				this->B.data[i] = 0;
		}

		initialized = this->B.data != NULL && this->M.data != NULL;
	};
	LinearAlgebra(
		size_t m, size_t n,
		double** M,
		double* B)
	{
		this->m = m;
		this->n = n;
		this->M.m = m;
		this->M.n = n;
		this->M.data = new double*[m];
		this->B.data = new double[n];

		if (M != NULL)
		{
			for (size_t i = 0; i < m; i++)
			{
				this->M.data[i] = new double[n];

				for (size_t j = 0; j < n; j++)
					this->M.data[i][j] = M[i][j];
			}
		}

		if (B != NULL)
		{
			this->B.data = new double[n];

			for (size_t i = 0; i < m; i++)
				this->B.data[i] = B[i];
		}

		initialized = this->B.data != NULL && this->M.data != NULL;
	}
	~LinearAlgebra()
	{
		M.m = m;
		M.n = n;
		B.n = n;

		if (B.data != NULL)
			delete[] B.data;

		for (size_t i = 0; i < m; i++)
			if (M.data[i] != NULL)
				delete[] M.data[i];

		if (M.data != NULL)
			delete[] M.data;
	}
	double DblDeterminant(bool failure);
	Vector<double> DblGaussianElimination(
		bool& failure);
	// The following four methods are from the
	// textbook "Elementary Numerical Analysis
	// An Algorithmic Approach" by S. D. Conte
	// and Carl de Boor Translated from the
	// original FORTRAN by James Pate Williams, Jr.
	// Copyright (c) 2023 All Rights Reserved
	bool DblGaussianFactor(
		Vector<int>& pivot);
	bool DblGaussianSolution(
		Vector<double>& x,
		Vector<int>& pivot);
	bool DblSubstitution(
		Vector<double>& x,
		Vector<int>& pivot);
	bool DblInverse(
		Matrix<double>& A,
		Vector<int>& pivot);
	// Henri Cohen Algorithm 2.2.7
	void DblCharPolyAndAdjoint(
		Matrix<double>& adjoint,
		Vector<double>& a);
	// Henri Cohen Algorithm 2.3.1
	void DblMatrixKernel(
		Matrix<double>& X, size_t& r);
	// Henri Cohen Algorithm 2.3.1
	void DblMatrixImage(
		Matrix<double>& N, size_t& rank);
};

// pch.h: This is a precompiled header file.
// Files listed below are compiled only once, improving build performance for future builds.
// This also affects IntelliSense performance, including code completion and many code browsing features.
// However, files listed here are ALL re-compiled if any one of them is updated between builds.
// Do not add files here that you will be updating frequently as this negates the performance advantage.

#ifndef PCH_H
#define PCH_H
#include <fstream>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
#endif //PCH_H

#include "pch.h"
#include "LinearAlgebra.h"

double LinearAlgebra::DblDeterminant(
    bool failure)
{
    double deter = 1;
    Vector<int> pivot(n);

    if (!initialized || m != n)
    {
        failure = true;
        return 0.0;
    }

    if (!DblGaussianFactor(pivot))
    {
        failure = true;
        return 0.0;
    }

    for (size_t i = 0; i < n; i++)
        deter *= M.data[i][i];

    return deter;
}

Vector<double> LinearAlgebra::DblGaussianElimination(
    bool& failure)
{
    double* C = new double[m];
    Vector<double> X(n);

    X.data = new double[n];

    if (X.data == NULL)
        exit(-200);

    if (!initialized)
    {
        failure = true;
        delete[] C;
        return X;
    }
    
    for (size_t i = 0; i < m; i++)
        C[i] = -1;

    failure = false;

    for (size_t j = 0; j < n; j++)
    {
        bool found = false;
        size_t i = j;

        while (i < n && !found)
        {
            if (M.data[i][j] != 0)
                found = true;
            else
                i++;
        }

        if (!found)
        {
            failure = true;
            break;
        }

        if (i > j)
        {
            for (size_t l = j; l < n; l++)
            {
                double t = M.data[i][l];
                M.data[i][l] = M.data[j][l];
                M.data[j][l] = t;
                t = B.data[i];
                B.data[i] = B.data[j];
                B.data[j] = t;
            }
        }

        double d = 1.0 / M.data[j][j];

        for (size_t k = j + 1; k < n; k++)
            C[k] = d * M.data[k][j];

        for (size_t k = j + 1; k < n; k++)
        {
            for (size_t l = j + 1; l < n; l++)
                M.data[k][l] = M.data[k][l] - C[k] * M.data[j][l];
            
            B.data[k] = B.data[k] - C[k] * B.data[j];
        }
    }

    for (int i = (int)n - 1; i >= 0; i--)
    {
        double sum = 0;

        for (size_t j = i + 1; j < n; j++)
            sum += M.data[i][j] * X.data[j];

        X.data[i] = (B.data[i] - sum) / M.data[i][i];
    }

    delete[] C;
    return X;
}

bool LinearAlgebra::DblGaussianFactor(
    Vector<int>& pivot)
    // returns false if matrix is singular
{
    Vector<double> d(n);
    double awikod, col_max, ratio, row_max, temp;
    int flag = 1;
    size_t i_star, itemp;

    for (size_t i = 0; i < n; i++)
    {
        pivot.data[i] = i;
        row_max = 0;
        for (size_t j = 0; j < n; j++)
            row_max = max(row_max, abs(M.data[i][j]));
        if (row_max == 0)
        {
            flag = 0;
            row_max = 1;
        }
        d.data[i] = row_max;
    }
    if (n <= 1) return flag != 0;
    // factorization
    for (size_t k = 0; k < n - 1; k++)
    {
        // determine pivot row the row i_star
        col_max = abs(M.data[k][k]) / d.data[k];
        i_star = k;
        for (size_t i = k + 1; i < n; i++)
        {
            awikod = abs(M.data[i][k]) / d.data[i];
            if (awikod > col_max)
            {
                col_max = awikod;
                i_star = i;
            }
        }
        if (col_max == 0)
            flag = 0;
        else
        {
            if (i_star > k)
            {
                // make k the pivot row by
                // interchanging with i_star
                flag *= -1;
                itemp = pivot.data[i_star];
                pivot.data[i_star] = pivot.data[k];
                pivot.data[k] = itemp;
                temp = d.data[i_star];
                d.data[i_star] = d.data[k];
                d.data[k] = temp;
                for (size_t j = 0; j < n; j++)
                {
                    temp = M.data[i_star][j];
                    M.data[i_star][j] = M.data[k][j];
                    M.data[k][j] = temp;
                }
            }
            // eliminate x[k]
            for (size_t i = k + 1; i < n; i++)
            {
                M.data[i][k] /= M.data[k][k];
                ratio = M.data[i][k];
                for (size_t j = k + 1; j < n; j++)
                    M.data[i][j] -= ratio * M.data[k][j];
            }
        }

        if (M.data[n - 1][n - 1] == 0) flag = 0;
    }

    if (flag == 0)
        return false;

    return true;
}

bool LinearAlgebra::DblGaussianSolution(
    Vector<double>& x,
    Vector<int>& pivot)
{
    if (!DblGaussianFactor(pivot))
        return false;

    return DblSubstitution(x, pivot);
}

bool LinearAlgebra::DblSubstitution(
    Vector<double>& x,
    Vector<int>& pivot)
{
    double sum;
    size_t j, n1 = n - 1;

    if (n == 1)
    {
        x.data[0] = B.data[0] / M.data[0][0];
        return true;
    }

    // forward substitution

    x.data[0] = B.data[pivot.data[0]];

    for (int i = 1; i < (int)n; i++)
    {
        for (j = 0, sum = 0; j < (size_t)i; j++)
            sum += M.data[i][j] * x.data[j];

        x.data[i] = B.data[pivot.data[i]] - sum;
    }

    // backward substitution

    x.data[n1] /= M.data[n1][n1];

    for (int i = n - 2; i >= 0; i--)
    {
        double sum = 0.0;

        for (j = i + 1; j < n; j++)
            sum += M.data[i][j] * x.data[j];

        x.data[i] = (x.data[i] - sum) / M.data[i][i];
    }

    return true;
}

bool LinearAlgebra::DblInverse(
    Matrix<double>& A,
    Vector<int>& pivot)
{
    Vector<double> x(n);

    if (!DblGaussianFactor(pivot))
        return false;

    for (size_t i = 0; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
            B.data[j] = 0;
    }
    
    for (size_t i = 0; i < n; i++)
    {
        B.data[i] = 1;

        if (!DblSubstitution(x, pivot))
            return false;

        B.data[i] = 0;

        for (size_t j = 0; j < n; j++)
           A.data[i][j] = x.data[pivot.data[j]];
    }

    return true;
}

void LinearAlgebra::DblCharPolyAndAdjoint(
    Matrix<double>& adjoint,
    Vector<double>& a)
{
    Matrix<double> C(n, n);
    Matrix<double> I(n, n);

    for (size_t i = 0; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
            C.data[i][j] = I.data[i][j] = 0;
    }

    for (size_t i = 0; i < n; i++)
        C.data[i][i] = I.data[i][i] = 1;

    a.data[0] = 1;

    for (size_t i = 1; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
        {
            for (size_t k = 0; k < n; k++)
            {
                double sum = 0.0;

                for (size_t l = 0; l < n; l++)
                    sum += M.data[j][l] * C.data[l][k];

                C.data[j][k] = sum;
            }
        }

        double tr = 0.0;

        for (size_t j = 0; j < n; j++)
            tr += C.data[j][j];

        a.data[i] = -tr / i;

        for (size_t j = 0; j < n; j++)
        {
            for (size_t k = 0; k < n; k++)
                C.data[j][k] += a.data[i] * I.data[j][k];
        }
    }

    for (size_t i = 0; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
        {
            double sum = 0.0;

            for (size_t k = 0; k < n; k++)
                sum += M.data[i][k] * C.data[k][j];

            C.data[i][j] = sum;
        }
    }

    double trace = 0.0;

    for (size_t i = 0; i < n; i++)
        trace += C.data[i][i];

    trace /= n;
    a.data[n - 1] = -trace;

    double factor = 1.0;

    if ((n - 1) % 2 != 0)
        factor = -1.0;

    for (size_t i = 0; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
            adjoint.data[i][j] = factor * C.data[i][j];
    }
}

void LinearAlgebra::DblMatrixKernel(Matrix<double>& X, size_t& r)
{
    double D = 0.0;
    Vector<int> c(m);
    Vector<int> d(n);

    r = 0;

    for (size_t i = 0; i < m; i++)
        c.data[i] = -1;

    size_t j, k = 1;
Step2:
    for (j = 0; j < m; j++)
    {
        if (M.data[j][k] != 0 && c.data[j] == -1)
            break;
    }

    if (j == m)
    {
        r++;
        d.data[k] = 0;
        goto Step4;
    }

    D = -1.0 / M.data[j][k];

    M.data[j][k] = -1;

    for (size_t s = k + 1; s < n; s++)
    {
        M.data[j][s] = D * M.data[j][s];

        for (size_t i = 0; i < m; i++)
        {
            if (i != j)
            {
                D = M.data[i][k];
                M.data[i][k] = 0;
            }
        }
    }

    for (size_t s = k + 1; s < n; s++)
    {
        for (size_t i = 0; i < m; i++)
        {
            M.data[i][s] += D * M.data[j][s];
        }
    }

    c.data[j] = k;
    d.data[k] = j;
Step4:
    if (k < n - 1)
    {
        k++;
        goto Step2;
    }

    X.n = n;

    if (r != 0)
    {
        for (k = 0; k < n; k++)
        {
            if (d.data[k] == 0)
            {
                for (size_t i = 0; i < n; i++)
                {
                    if (d.data[i] > 0)
                        X.data[k][i] = M.data[d.data[i]][k];
                    else if (i == k)
                        X.data[k][i] = 1;
                    else
                        X.data[k][i] = 0;
                }
            }
        }
    }
}

void LinearAlgebra::DblMatrixImage(
    Matrix<double>& N, size_t& rank)
{
    double D = 0.0;
    size_t r = 0;
    Matrix<double> copyM(m, n);
    Vector<int> c(m);
    Vector<int> d(n);

    for (size_t i = 0; i < m; i++)
        c.data[i] = -1;

    size_t j, k = 1;
    N = copyM = M;
Step2:
    for (j = 0; j < m; j++)
    {
        if (copyM.data[j][k] != 0 && c.data[j] == -1)
            break;
    }

    if (j == m)
    {
        r++;
        d.data[k] = 0;
        goto Step4;
    }

    D = -1.0 / copyM.data[j][k];

    copyM.data[j][k] = -1;

    for (size_t s = k + 1; s < n; s++)
    {
        copyM.data[j][s] = D * copyM.data[j][s];

        for (size_t i = 0; i < m; i++)
        {
            if (i != j)
            {
                D = copyM.data[i][k];
                copyM.data[i][k] = 0;
            }
        }
    }

    for (size_t s = k + 1; s < n; s++)
    {
        for (size_t i = 0; i < m; i++)
        {
            copyM.data[i][s] += D * copyM.data[j][s];
        }
    }

    c.data[j] = k;
    d.data[k] = j;
Step4:
    if (k < n - 1)
    {
        k++;
        goto Step2;
    }

    rank = n - r;

    for (j = 0; j < m; j++)
    {
        if (c.data[j] != 0)
        {
            for (size_t i = 0; i < m; i++)
            {
                N.data[i][c.data[j]] = M.data[i][c.data[j]];
            }
        }
    }
}

/*
** Cohen's linear algebra test program
** Implemented by James Pate Williams, Jr.
** Copyright (c) 2023 All Rights Reserved
*/

#include "pch.h"
#include "LinearAlgebra.h"

double GetDblNumber(fstream& inps)
{
    char ch = inps.get();
    string numberStr;

    while (ch == ' ' || ch == '\t' || ch == '\r' || ch == '\n')
        ch = inps.get();

    while (ch == '+' || ch == '-' || ch == '.' ||
        ch >= '0' && ch <= '9')
    {
        numberStr += ch;
        ch = inps.get();
    }

    double x = atof(numberStr.c_str());
    return x;
}

int GetIntNumber(fstream& inps)
{
    char ch = inps.get();
    string numberStr;

    while (ch == ' ' || ch == '\t' || ch == '\r' || ch == '\n')
        ch = inps.get();

    while (ch == '+' || ch == '-' || ch >= '0' && ch <= '9')
    {
        numberStr += ch;
        ch = inps.get();
    }

    int x = atoi(numberStr.c_str());
    return x;
}

int main()
{
    fstream inps;

    inps.open("CLATestFile.txt", fstream::in);
    
    if (inps.fail())
    {
        cout << "Input file opening error!" << endl;
        return -1;
    }

    fstream outs;

    outs.open("CLAResuFile.txt", fstream::out | fstream::ate);

    if (outs.fail())
    {
        cout << "Output file opening error!" << endl;
        return -2;
    }

    size_t m, n;
    
    while (!inps.eof())
    {
        char buffer[256] = { '\0' };

        inps.getline(buffer, 256);
        m = GetIntNumber(inps);

        if (inps.eof())
            return 0;

        if (m < 1)
        {
            cout << "The number of rows must be >= 1" << endl;
            return -100;
        }

        n = GetIntNumber(inps);

        if (n < 1)
        {
            cout << "The number of colums must be >= 1" << endl;
            return -101;
        }

        LinearAlgebra la(m, n);
        Matrix<double> copyM(m, n);
        Vector<double> copyB(n);

        inps.getline(buffer, 256);

        for (size_t i = 0; i < m; i++)
        {
            for (size_t j = 0; j < n; j++)
            {
                double x = GetDblNumber(inps);

                la.M.data[i][j] = x;
                copyM.data[i][j] = x;
            }
        }

        inps.getline(buffer, 256);

        for (size_t i = 0; i < n; i++)
        {
            la.B.data[i] = GetDblNumber(inps);
            copyB.data[i] = la.B.data[i];
        }

        bool failure = false;
        Vector<double> X = la.DblGaussianElimination(failure);

        if (!failure)
        {
            outs << "The 1st solution of the linear system of equations:" << endl;
            X.OutputVector(outs, ' ', 5, 8);
        }
        else
        {
            cout << "Cohen Gaussian elimination failure!" << endl;
            exit(-102);
        }

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        Matrix<double> A(n, n);
        Vector<int> pivot(n);

        if (!la.DblGaussianSolution(X, pivot))
            exit(-103);

        outs << "The 2nd solution of the linear system of equations:" << endl;

        X.OutputVector(outs, ' ', 5, 8);

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        double deter = la.DblDeterminant(failure);

        outs << "The determinant of the linear system of equations:" << endl;
        outs << deter << endl;

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        outs << "The inverse of the linear system of equations:" << endl;

        if (!la.DblInverse(A, pivot))
        {
            cout << "Conte Gaussian inverse matrix failure!" << endl;
            exit(-104);
        }

        else
            A.OutputMatrix(outs, ' ', 5, 8);

        Matrix<double> adjoint(n, n);
        Vector<double> a(n);

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        la.DblCharPolyAndAdjoint(adjoint, a);
        outs << "The adjoint of the linear system of equations:" << endl;
        adjoint.OutputMatrix(outs, ' ', 5, 8);
        outs << "The characteristic polynomial of the linear system of equations:" << endl;
        a.OutputVector(outs, ' ', 5, 8);

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        Matrix<double> kernel(m, n);
        size_t r = 0;

        la.DblMatrixKernel(kernel, r);

        if (r > 0)
        {
            outs << "The kernel of the matrix: " << endl;
            kernel.OutputMatrix(outs, ' ', 5, 8);
            outs << "Dimension of the kernel: " << r << endl;
        }

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        Matrix<double> N(m, n);
        size_t rank;

        la.DblMatrixImage(N, rank);

        if (rank > 0)
        {
            outs << "The image of the matrix: " << endl;
            N.OutputMatrix(outs, ' ', 5, 8);
            outs << "Rank = " << rank << endl;
        }
    }

    inps.close();
    outs.close();
}

Part of a New Linear Algebra Package in C++ Implemented by James Pate Williams, Jr.

// Algorithms from "A Course in Computational
// Algebraic Number Theory" by Henri Cohen
// Implemented by James Pate Williams, Jr.
// Copyright (c) 2023 All Rights Reserved

#pragma once
#include "pch.h"

template<class T> class Matrix
{
public:
	size_t m, n;
	T** data;

	Matrix() { m = 0; n = 0; data = NULL; };
	Matrix(size_t m, size_t n)
	{
		this->m = m;
		this->n = n;
		data = new T*[m];

		if (data == NULL)
			exit(-300);

		for (size_t i = 0; i < m; i++)
		{
			data[i] = new T[n];

			if (data[i] == NULL)
				exit(-301);
		}
	};
	void OutputMatrix(
		fstream& outs, char fill, int precision, int width)
	{
		for (size_t i = 0; i < m; i++)
		{
			for (size_t j = 0; j < n; j++)
			{
				outs << setfill(fill) << setprecision(precision);
				outs << setw(width) << data[i][j] << '\t';
			}

			outs << endl;
		}
	};
};

template<class T> class Vector
{
public:
	size_t n;
	T* data;

	Vector() { n = 0; data = NULL; };
	Vector(size_t n)
	{
		this->n = n;
		data = new T[n];
	};
	void OutputVector(
		fstream& outs, char fill, int precision, int width)
	{
		for (size_t i = 0; i < n; i++)
		{
			outs << setfill(fill) << setprecision(precision);
			outs << setw(width) << data[i] << '\t';
		}

		outs << endl;
	};
};

class LinearAlgebra
{
public:
	bool initialized;
	size_t m, n;
	Matrix<double> M;
	Vector<double> B;

	LinearAlgebra() { 
		initialized = false;
		m = 0; n = 0;
		M.data = NULL;
		B.data = NULL;
	};
	LinearAlgebra(size_t m, size_t n) {
		initialized = false;
		this->m = m;
		this->n = n;
		this->M.m = m;
		this->M.n = n;
		this->B.n = n;
		this->M.data = new double*[m];
		this->B.data = new double[n];

		if (M.data != NULL)
		{
			for (size_t i = 0; i < m; i++)
			{
				this->M.data[i] = new double[n];

				for (size_t j = 0; j < n; j++)
					this->M.data[i][j] = 0;
			}
		}

		if (B.data != NULL)
		{
			this->B.data = new double[n];

			for (size_t i = 0; i < n; i++)
				this->B.data[i] = 0;
		}

		initialized = this->B.data != NULL && this->M.data != NULL;
	};
	LinearAlgebra(
		size_t m, size_t n,
		double** M,
		double* B)
	{
		this->m = m;
		this->n = n;
		this->M.m = m;
		this->M.n = n;
		this->M.data = new double*[m];

		if (M != NULL)
		{
			for (size_t i = 0; i < m; i++)
			{
				this->M.data[i] = new double[n];

				for (size_t j = 0; j < n; j++)
					this->M.data[i][j] = M[i][j];
			}
		}

		if (B != NULL)
		{
			this->B.data = new double[n];

			for (size_t i = 0; i < m; i++)
				this->B.data[i] = B[i];
		}

		initialized = this->B.data != NULL && this->M.data != NULL;
	}
	~LinearAlgebra()
	{
		M.m = m;
		M.n = n;
		B.n = n;

		if (B.data != NULL)
			delete[] B.data;

		for (size_t i = 0; i < m; i++)
			if (M.data[i] != NULL)
				delete[] M.data[i];

		if (M.data != NULL)
			delete[] M.data;
	}
	double DblDeterminant(size_t n, bool failure);
	Vector<double> DblGaussianElimination(
		bool& failure);
	// The following three methods are from the
	// textbook "Elementary Numerical Analysis
	// An Algorithmic Approach" by S. D. Conte
	// and Carl de Boor Translated from the
	// original FORTRAN by James Pate Williams, Jr.
	// Copyright (c) 2023 All Rights Reserved
	bool DblGaussianFactor(
		size_t n,
		Vector<int>& pivot);
	bool DblGaussianSolution(
		int n,
		Vector<double>& x,
		Vector<int>& pivot);
	bool DblSubstitution(
		size_t n,
		Vector<double>& x,
		Vector<int>& pivot);
	bool DblInverse(
		size_t n,
		Matrix<double>& A,
		Vector<int>& pivot);
};

#include "pch.h"
#include "LinearAlgebra.h"

double LinearAlgebra::DblDeterminant(
    size_t n, bool failure)
{
    double deter = 1;
    Vector<int> pivot(n);

    if (!initialized || m != n)
    {
        failure = true;
        return 0.0;
    }

    if (!DblGaussianFactor(n, pivot))
    {
        failure = true;
        return 0.0;
    }

    for (size_t i = 0; i < n; i++)
        deter *= M.data[i][i];

    return deter;
}

Vector<double> LinearAlgebra::DblGaussianElimination(
    bool& failure)
{
    double* C = new double[m];
    Vector<double> X(n);

    X.data = new double[n];

    if (X.data == NULL)
        exit(-200);

    if (!initialized)
    {
        failure = true;
        delete[] C;
        return X;
    }
    
    for (size_t i = 0; i < m; i++)
        C[i] = -1;

    failure = false;

    for (size_t j = 0; j < n; j++)
    {
        bool found = false;
        size_t i = j;

        while (i < n && !found)
        {
            if (M.data[i][j] != 0)
                found = true;
            else
                i++;
        }

        if (!found)
        {
            failure = true;
            break;
        }

        if (i > j)
        {
            for (size_t l = j; l < n; l++)
            {
                double t = M.data[i][l];
                M.data[i][l] = M.data[j][l];
                M.data[j][l] = t;
                t = B.data[i];
                B.data[i] = B.data[j];
                B.data[j] = t;
            }
        }

        double d = 1.0 / M.data[j][j];

        for (size_t k = j + 1; k < n; k++)
            C[k] = d * M.data[k][j];

        for (size_t k = j + 1; k < n; k++)
        {
            for (size_t l = j + 1; l < n; l++)
                M.data[k][l] = M.data[k][l] - C[k] * M.data[j][l];
            
            B.data[k] = B.data[k] - C[k] * B.data[j];
        }
    }

    for (int i = (int)n - 1; i >= 0; i--)
    {
        double sum = 0;

        for (size_t j = i + 1; j < n; j++)
            sum += M.data[i][j] * X.data[j];

        X.data[i] = (B.data[i] - sum) / M.data[i][i];
    }

    delete[] C;
    return X;
}

bool LinearAlgebra::DblGaussianFactor(
    size_t n,
    Vector<int>& pivot)
    // returns false if matrix is singular
{
    Vector<double> d(n);
    double awikod, col_max, ratio, row_max, temp;
    int flag = 1;
    size_t i_star, itemp;

    for (size_t i = 0; i < n; i++)
    {
        pivot.data[i] = i;
        row_max = 0;
        for (size_t j = 0; j < n; j++)
            row_max = max(row_max, abs(M.data[i][j]));
        if (row_max == 0)
        {
            flag = 0;
            row_max = 1;
        }
        d.data[i] = row_max;
    }
    if (n <= 1) return flag != 0;
    // factorization
    for (size_t k = 0; k < n - 1; k++)
    {
        // determine pivot row the row i_star
        col_max = abs(M.data[k][k]) / d.data[k];
        i_star = k;
        for (size_t i = k + 1; i < n; i++)
        {
            awikod = abs(M.data[i][k]) / d.data[i];
            if (awikod > col_max)
            {
                col_max = awikod;
                i_star = i;
            }
        }
        if (col_max == 0)
            flag = 0;
        else
        {
            if (i_star > k)
            {
                // make k the pivot row by
                // interchanging with i_star
                flag *= -1;
                itemp = pivot.data[i_star];
                pivot.data[i_star] = pivot.data[k];
                pivot.data[k] = itemp;
                temp = d.data[i_star];
                d.data[i_star] = d.data[k];
                d.data[k] = temp;
                for (size_t j = 0; j < n; j++)
                {
                    temp = M.data[i_star][j];
                    M.data[i_star][j] = M.data[k][j];
                    M.data[k][j] = temp;
                }
            }
            // eliminate x[k]
            for (size_t i = k + 1; i < n; i++)
            {
                M.data[i][k] /= M.data[k][k];
                ratio = M.data[i][k];
                for (size_t j = k + 1; j < n; j++)
                    M.data[i][j] -= ratio * M.data[k][j];
            }
        }

        if (M.data[n - 1][n - 1] == 0) flag = 0;
    }

    if (flag == 0)
        return false;

    return true;
}

bool LinearAlgebra::DblGaussianSolution(
    int n,
    Vector<double>& x,
    Vector<int>& pivot)
{
    if (!DblGaussianFactor(n, pivot))
        return false;

    return DblSubstitution(n, x, pivot);
}

bool LinearAlgebra::DblSubstitution(
    size_t n, Vector<double>& x,
    Vector<int>& pivot)
{
    double sum;
    size_t j, n1 = n - 1;

    if (n == 1)
    {
        x.data[0] = B.data[0] / M.data[0][0];
        return true;
    }

    // forward substitution

    x.data[0] = B.data[pivot.data[0]];

    for (int i = 1; i < (int)n; i++)
    {
        for (j = 0, sum = 0; j < (size_t)i; j++)
            sum += M.data[i][j] * x.data[j];

        x.data[i] = B.data[pivot.data[i]] - sum;
    }

    // backward substitution

    x.data[n1] /= M.data[n1][n1];

    for (int i = n - 2; i >= 0; i--)
    {
        double sum = 0.0;

        for (j = i + 1; j < n; j++)
            sum += M.data[i][j] * x.data[j];

        x.data[i] = (x.data[i] - sum) / M.data[i][i];
    }

    return true;
}

bool LinearAlgebra::DblInverse(
    size_t n,
    Matrix<double>& A,
    Vector<int>& pivot)
{
    Vector<double> x(n);

    if (!DblGaussianFactor(n, pivot))
        return false;

    for (size_t i = 0; i < n; i++)
    {
        for (size_t j = 0; j < n; j++)
            B.data[j] = 0;
    }
    
    for (size_t i = 0; i < n; i++)
    {
        B.data[i] = 1;

        if (!DblSubstitution(n, x, pivot))
            return false;

        B.data[i] = 0;

        for (size_t j = 0; j < n; j++)
           A.data[i][j] = x.data[pivot.data[j]];
    }

    return true;
}

/*
** Cohen's linear algebra test program
** Implemented by James Pate Williams, Jr.
** Copyright (c) 2023 All Rights Reserved
*/

#include "pch.h"
#include "LinearAlgebra.h"

double GetDblNumber(fstream& inps)
{
    char ch = inps.get();
    string numberStr;

    while (ch == ' ' || ch == '\t' || ch == '\r' || ch == '\n')
        ch = inps.get();

    while (ch == '+' || ch == '-' || ch == '.' ||
        ch >= '0' && ch <= '9')
    {
        numberStr += ch;
        ch = inps.get();
    }

    double x = atof(numberStr.c_str());
    return x;
}

int GetIntNumber(fstream& inps)
{
    char ch = inps.get();
    string numberStr;

    while (ch == ' ' || ch == '\t' || ch == '\r' || ch == '\n')
        ch = inps.get();

    while (ch == '+' || ch == '-' || ch >= '0' && ch <= '9')
    {
        numberStr += ch;
        ch = inps.get();
    }

    int x = atoi(numberStr.c_str());
    return x;
}

int main()
{
    fstream inps;

    inps.open("CLATestFile.txt", fstream::in);
    
    if (inps.fail())
    {
        cout << "Input file opening error!" << endl;
        return -1;
    }

    fstream outs;

    outs.open("CLAResuFile.txt", fstream::out | fstream::ate);

    if (outs.fail())
    {
        cout << "Output file opening error!" << endl;
        return -2;
    }

    size_t m, n;
    
    while (!inps.eof())
    {
        m = GetIntNumber(inps);

        if (inps.eof())
            return 0;

        if (m < 1)
        {
            cout << "The number of rows must be >= 1" << endl;
            return -100;
        }

        n = GetIntNumber(inps);

        if (n < 1)
        {
            cout << "The number of rows must be >= 1" << endl;
            return -101;
        }

        LinearAlgebra la(m, n);
        Matrix<double> copyM(m, n);
        Vector<double> copyB(n);

        for (size_t i = 0; i < m; i++)
        {
            for (size_t j = 0; j < n; j++)
            {
                double x = GetDblNumber(inps);

                la.M.data[i][j] = x;
                copyM.data[i][j] = x;
            }
        }

        for (size_t i = 0; i < n; i++)
        {
           la.B.data[i] = GetDblNumber(inps);
           copyB.data[i] = la.B.data[i];
        }

        bool failure = false;
        Vector<double> X = la.DblGaussianElimination(failure);

        if (!failure)
            X.OutputVector(outs, ' ', 5, 8);
        else
        {
            cout << "Cohen Gaussian elimination failure!" << endl;
            exit(-102);
        }


        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        Matrix<double> A(n, n);
        Vector<int> pivot(n);
        
        if (!la.DblGaussianSolution(n, X, pivot))
            exit(-103);

        X.OutputVector(outs, ' ', 5, 8);

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        double deter = la.DblDeterminant(n, failure);

        outs << deter << endl;

        for (size_t i = 0; i < m; i++)
        {
            la.B.data[i] = copyB.data[i];

            for (size_t j = 0; j < n; j++)
            {
                la.M.data[i][j] = copyM.data[i][j];
            }
        }

        if (!la.DblInverse(n, A, pivot))
        {
            cout << "Conte Gaussian inverse matrix failure!" << endl;
            exit(-104);
        }

        else
            A.OutputMatrix(outs, ' ', 5, 8);
    }

    inps.close();
    outs.close();
}

       3	       4	
       3	       4	
1
       2	      -1	
      -1	       1	
       5	       2	
       5	       2	
2
     1.5	    -0.5	
    -0.5	     0.5	
 0.61111	 0.44444	
 0.61111	 0.44444	
36
 0.22222	-0.11111	
-0.083333	 0.16667	
    -1.4	       5	
    -1.4	       5	
-10
    -0.4	       1	
     0.3	    -0.5	
       2	       3	      -1	
       2	       3	      -1	
1
       4	       5	      -2	
       3	       4	      -2	
      -1	      -1	       1

Huffman Compression in C++ Implemented by James Pate Williams, Jr.

The original string is:
abbbccddeefffghhhhijkllmm

# characters = 25
The compressed codes and frequencies are:
  0     e         2
  1     l         2
  2     f         3
  3     b         3
  4     i         1
  5     c         2
  6     g         1
  7     a         1
  8     d         2
  9     m         2
 10     k         1
 11     j         1
 12     h         4
# leaf nodes = 13
% compressed = 48

C:\Users\james\source\repos\HuffmanCodes\Debug\HuffmanCodes.exe (process 36772) exited with code 0.
Press any key to close this window . . .

// Algorithm is found in the textbook
// "Introduction to Algorithms"
// by Thomas H. Cormen, Charles E.
// Leiserson, Ronald L. Rivest p. 340

#include "pch.h"

int leafNodes = 0;

void InorderTraversal(BinaryTreeNode<CharFreq>* node)
{
    if (node != NULL)
    {
        InorderTraversal(node->lt);

        if (node->lt == NULL && node->rt == NULL)
        {
            CharFreq cf = node->data;

            std::cout << setw(3) << leafNodes << '\t';
            std::cout << cf.ch << '\t';
            std::cout << setw(3) << cf.freq << '\n';
            leafNodes++;
        }
        
        InorderTraversal(node->rt);
    }
}

int main()
{
    int f[128] = { 0 };
    string str = "abbbccddeefffghhhhijkllmm";
    BinaryTreeNode<CharFreq> charFreqTree;
    vector<BinaryTreeNode<CharFreq>> v;

    std::cout << "The original string is: " << endl;
    std::cout << str << endl << endl;

    for (size_t i = 0; i < strlen(str.c_str()); i++)
    {
        bool found = false;
        char ch = str.c_str()[i];

        for (auto iter = v.begin(); !found &&
            iter != v.end(); iter++)
        {
            BinaryTreeNode<CharFreq> node = *iter;

            if (node.data.ch == ch)
            {
                node.data.freq++;
                *iter = node;
                found = true;
            }
        }

        if (!found)
        {
            BinaryTreeNode<CharFreq> node;

            node.data.ch = ch;
            node.data.freq = 1;
            node.lt = node.rt = NULL;
            v.push_back(node);
        }
    }

    priority_queue<BinaryTreeNode<CharFreq>, vector<BinaryTreeNode<CharFreq>>,
        greater<BinaryTreeNode<CharFreq>>> Q(v.begin(), v.end());

    size_t n = Q.size();
   
    for (size_t i = 0; i < n - 1; i++)
    {
        BinaryTreeNode<CharFreq>* x = new
            BinaryTreeNode<CharFreq>();
        BinaryTreeNode<CharFreq>* y = new
            BinaryTreeNode<CharFreq>();
        *x = Q.top();
        Q.pop();
        *y = Q.top();
        Q.pop();

        CharFreq charFreq;
        charFreq.ch = (char)(x->data.ch + y->data.ch);
        charFreq.freq = x->data.freq + y->data.freq;

        BinaryTreeNode<CharFreq>* z = new
            BinaryTreeNode<CharFreq>(charFreq, x, y);

        Q.push(*z);
    }

    BinaryTreeNode<CharFreq> root = Q.top();
    std::cout << "# characters = " << strlen(str.c_str()) << endl;
    std::cout << "The compressed codes and frequencies are:" << endl;
    InorderTraversal(&root);
    std::cout << "# leaf nodes = " << leafNodes << endl;
    std::cout << "% compressed = " <<
        (100.0 - 100.0 * ((double)leafNodes) / strlen(str.c_str())) << endl;
    return 0;
}

#pragma once
#include "pch.h"
using namespace std;

template <class T>
	class BinaryTreeNode
	{
	public:
		T data;
		BinaryTreeNode* lt;
		BinaryTreeNode* rt;

		BinaryTreeNode() { 
			lt = rt = nullptr;
		};

		BinaryTreeNode(T data)
		{
			this->data = data;
			lt = rt = nullptr;
		};

		BinaryTreeNode(T data, BinaryTreeNode* lt, BinaryTreeNode* rt)
		{
			this->data = data;
			this->lt = lt;
			this->rt = rt;
		};

		friend bool operator > (BinaryTreeNode lhs, BinaryTreeNode rhs)
		{
			return lhs.data > rhs.data;
		};

		friend bool operator < (BinaryTreeNode lhs, BinaryTreeNode rhs)
		{
			return lhs.data < rhs.data;
		};

		friend bool operator == (BinaryTreeNode lhs, BinaryTreeNode rhs)
		{
			return lhs.data == rhs.data;
		};
	};

#pragma once
class CharFreq
{
public:
	char ch;
	int freq;
	
	CharFreq()
	{
		ch = '\0';
		freq = 0;
	};
	CharFreq(char c)
	{
		ch = c;
		freq = 0;
	};
	CharFreq(char c, int f)
	{
		ch = c;
		freq = f;
	};

	friend int operator - (CharFreq lhs, CharFreq rhs)
	{
		return lhs.freq - rhs.freq;
	}

	friend bool operator > (CharFreq lhs, CharFreq rhs)
	{
		return lhs.freq > rhs.freq;
	};

	friend bool operator < (CharFreq lhs, CharFreq rhs)
	{
		return lhs.freq < rhs.freq;
	};

	friend bool operator == (CharFreq lhs, CharFreq rhs)
	{
		return lhs.freq == rhs.freq && lhs.ch == rhs.ch;
	};
};

// pch.h: This is a precompiled header file.
// Files listed below are compiled only once, improving build performance for future builds.
// This also affects IntelliSense performance, including code completion and many code browsing features.
// However, files listed here are ALL re-compiled if any one of them is updated between builds.
// Do not add files here that you will be updating frequently as this negates the performance advantage.

#ifndef PCH_H
#define PCH_H

// add headers that you want to pre-compile here
#include "BinaryTreeNode.h"
#include "CharFreq.h"
#include <iomanip>
#include <iostream>
#include <list>
#include <queue>
#include <string>
using namespace std;
#endif //PCH_H

Infix Notation to Postfix Notation and Postfix Evaluator Implemented by James Pate Williams, Jr.

I translated a Pascal program that is found in “Applied Data Structures Using Pascal” by Guy J. Hale and Richard J. Easton. The original Pascal program only used single digits and four arithmetic operators: ‘*’, ‘/’, ‘+’, and ‘-‘. I extended the code to multiple digit positive integers and added an exponentiation operator ‘^’. The priority of the operators is ‘^’, ‘*’, and ‘/’ highest value and ‘+’ and ‘-‘ lowest priority. I could easily add a modulus operator ‘%’ and Boolean bit operators. Extension to negative integers should be a facile operation. Below is the output from my C++ application.

3 + 7 * 8 - 5
3 7 8 * + 5 - 
Positive integer value = 54
3 * 7 - 4 / 2
3 7 * 4 2 / - 
Positive integer value = 19
(3 + 7) * 8 - 5
3 7 + 8 * 5 - 
Positive integer value = 75
(3 + 4) * 8 - (7 * 3 - 4)
3 4 + 8 * 7 3 * 4 - - 
Positive integer value = 39
(100 + 50) * 20 - 100 / 2
100 50 + 20 * 100 2 / - 
Positive integer value = 2950
2 ^ 16 - 5 * 100
2 16 ^ 5 100 * - 
Positive integer value = 65036

#pragma once
#include <list>
#include <stack>
#include <string>
#include <vector>
using namespace std;

const char Exp = '^';
const char Mul = '*';
const char Div = '/';
const char Add = '+';
const char Sub = '-';
const char LtParen = '(';
const char RtParen = ')';

class InfixToPostFix
{
public:
	stack<char> numberStack;
	
	int Convert(
		string infixStr, string& postfixStr);
	int EvaluatePostFix(string postfixStr);
	int Priority(char opcode);
};

#include "pch.h"
#include "InfixToPostFix.h"
#include <vector>
using namespace std;

int InfixToPostFix::Convert(
	string infixStr, string& postfixStr)
{
	char ch = 0;
	int number = 0, opcode = 0, opcode1 = 0, parenLevel = 0;
	string numberStr;

	for (size_t i = 0; i < infixStr.size();)
	{
		//while (i < infixStr.size() && infixStr[i] == ' ')
			//i++;

		while (i < infixStr.size() && infixStr[i] >= '0' &&
			infixStr[i] <= '9')
			numberStr.push_back(infixStr[i++]);

		if (numberStr.size() != 0)
		{
			for (size_t j = 0; j < numberStr.size(); j++)
				postfixStr.push_back(numberStr[j]);

			postfixStr.push_back(' ');
			numberStr.clear();
		}

		//while (i < infixStr.size() && infixStr[i] == ' ')
			//i++;

		if (infixStr[i] == '(')
		{
			numberStack.push(infixStr[i]);
			parenLevel++;
		}

		//while (i < infixStr.size() && infixStr[i] == ' ')
			//i++;

		if (infixStr[i] == ')')
		{
			ch = numberStack.top();
			numberStack.pop();

			parenLevel--;

			//while (i < infixStr.size() && infixStr[i] == ' ')
				//i++;

			while (ch != '(')
			{
				postfixStr.push_back(ch);
				postfixStr.push_back(' ');

				parenLevel++;

				ch = numberStack.top();
				numberStack.pop();
			}
		}

		//while (i < infixStr.size() && infixStr[i] == ' ')
			//i++;

		if (infixStr[i] == '^' || infixStr[i] == '*' ||
			infixStr[i] == '/' || infixStr[i] == '+' ||
			infixStr[i] == '-')
		{
			if (numberStack.empty())
				numberStack.push(infixStr[i]);
			else
			{
				ch = numberStack.top();
				numberStack.pop();

				//while (i < infixStr.size() && infixStr[i] == ' ')
					//i++;

				while (Priority(ch) >= Priority(infixStr[i]) &&
					!numberStack.empty() && ch != '(')
				{
					postfixStr.push_back(ch);
					postfixStr.push_back(' ');

					ch = numberStack.top();
					numberStack.pop();
				}

				//while (i < infixStr.size() && infixStr[i] == ' ')
					//i++;

				if (ch != '(')
				{
					if (Priority(infixStr[i]) <= Priority(ch))
					{
						postfixStr.push_back(ch);
						postfixStr.push_back(' ');

						numberStack.push(infixStr[i]);
					}

					else
					{
						numberStack.push(ch);
						numberStack.push(infixStr[i]);
					}
				}
				else
				{
					numberStack.push(ch);
					numberStack.push(infixStr[i]);
				}
			}
		}

		i++;
	}

	while (!numberStack.empty())
	{
		ch = numberStack.top();
		numberStack.pop();

		postfixStr.push_back(ch);
		postfixStr.push_back(' ');
	}

	return 0;
}

int InfixToPostFix::EvaluatePostFix(string postfixStr)
{
	char opcode = 0;
	int charValue = 0, result = 0, value1 = 0, value2 = 0;
	stack<int> intStack;

	for (size_t i = 0; i < postfixStr.size();)
	{
		string numberStr;

		if (postfixStr[i] != ' ')
		{
			while (postfixStr[i] >= '0' && postfixStr[i] <= '9')
				numberStr.push_back(postfixStr[i++]);

			if (!numberStr.empty())
				intStack.push(atoi(numberStr.c_str()));

			else
			{
				value2 = intStack.top();
				intStack.pop();
				value1 = intStack.top();
				intStack.pop();

				opcode = postfixStr[i++];

				if (opcode == '^')
					result = (int)pow(value1, value2);
				else if (opcode == '*')
					result = value1 * value2;
				else if (opcode == '/')
					result = value1 / value2;
				else if (opcode == '+')
					result = value1 + value2;
				else if (opcode == '-')
					result = value1 - value2;

				intStack.push(result);
			}
		}

		else
			i++;
	}

	result = intStack.top();
	intStack.pop();

	return result;
}

int InfixToPostFix::Priority(char opcode)
{
	int result = 0;

	switch (opcode)
	{
	case Exp:
		result = 2;
		break;
	case Mul:
		result = 2;
		break;
	case Div:
		result = 2;
		break;
	case Add:
		result = 1;
		break;
	case Sub:
		result = 1;
		break;
	case LtParen:
		result = 0;
	}

	return result;
}

#include "pch.h"
#include "InfixToPostFix.h"
#include <fstream>
#include <iostream>
#include <string>
using namespace std;

int main()
{
    fstream inps, outs;
    char line[256];
    
    inps.open("TestFile.txt", fstream::in);
    outs.open("ResuFile.txt", fstream::out | fstream::ate);

    while (!inps.eof())
    {
        string postfixStr;

        inps.getline(line, 256);

        if (strlen(line) == 0)
            break;

        string infixStr(line, strlen(line));
        InfixToPostFix translate;

        int con = translate.Convert(
            infixStr, postfixStr);

        if (con != 0)
        {
            cout << "Conversion error!" << endl;
            cout << "Error code = " << con << endl;
        }

        else
        {
            char newline[] = { '\n' };

            outs.write(infixStr.c_str(), infixStr.size());
            outs.write(newline, 1);
            outs.write(postfixStr.c_str(), postfixStr.size());
            outs.write(newline, 1);

            int val = translate.EvaluatePostFix(postfixStr);

            if (val < 0)
            {
                cout << "Evaluation error!" << endl;
                cout << "Error code = " << val << endl;
            }

            else
            {
                char buffer[256] = { '\0' };
                string str = "Positive integer value = ";

                _itoa_s(val, buffer, 10);
                
                outs.write(str.c_str(), strlen(str.c_str()));
                outs.write(buffer, strlen(buffer));
                outs.write(newline, 1);
            }
        }
    }

    inps.close();
    outs.close();

    return 0;
}

Arithmetic Expression Evaluator in C++ Implemented by James Pate Williams, Jr.

I translated to C++ and enhanced a Pascal arithmetic expression evaluator program found in “Applied Data Structures Using Pascal” by Guy J. Hale and Richard E. Easton. The original code used single digit numbers. As an exercise I enhanced the application to utilize multiple digit numbers. Below is my test file and output from my program. I used the C++ standard library stack data structure.

20 + 3 * 4 + 50 * 4 * 2 + 6 * 2 - 8 / 2 + 2 ^ 5

#pragma once
#include <fstream>
#include <stack>
using namespace std;

class Expression
{
public:
	char ch, sign, termOp;
	int number;

	stack<int> stk;

	void GetChar(fstream& inps);
	void GetExpression(fstream& inps);
	void GetFactor(fstream& inps);
	void GetTerm(fstream& inps);
};

#include "pch.h"
#include "Expression.h"
#include <math.h>
#include <fstream>
#include <stack>
#include <string>
using namespace std;

void Expression::GetChar(
	fstream& inps)
{
	while (!inps.eof())
	{
		ch = (char)inps.get();

		if (inps.eof())
			exit(1);

		if (ch >= '0' && ch <= '9')
			return;

		if (ch == '^' || ch == '*' || ch == '/')
			return;

		if (ch == '+' || ch == '-')
			return;

		if (ch == ' ' || ch == '\t' || ch == '\n')
			continue;

		if (ch == ';')
			return;
	}
}

void Expression::GetExpression(fstream& inps)
{
	int num, num1, num2;

	if (ch == '+' || ch == '-')
	{
		sign = ch;

		GetChar(inps);		
		GetTerm(inps);

		if (sign == '-')
		{
			num = stk.top();
			stk.pop();
			num = -num;
			stk.push(num);
		}
	}

	GetTerm(inps);
	
	while (ch == '+' || ch == '-')
	{
		termOp = ch;
		
		GetChar(inps);
		GetTerm(inps);
		
		num2 = stk.top();
		stk.pop();
		num1 = stk.top();
		stk.pop();

		if (termOp == '+')
			num = num1 + num2;
		else
			num = num1 - num2;

		stk.push(num);
	}
}

void Expression::GetFactor(fstream& inps)
{
	if (ch >= '0' && ch <= '9')
	{
		string str;

		while (ch >= '0' && ch <= '9' && !inps.eof())
		{
			str += ch;
			ch = (char)inps.get();

			if (ch == ' ' || ch == '\t' || ch == '\n')
				break;

			else if (ch == '^' || ch == '+' || ch == '-' ||
				ch == '*' || ch == '/')
				break;
		}

		if (inps.eof())
			exit(-1);

		while (ch == ' ' || ch == '\t' || ch == '\n')
			ch = (char)inps.get();

		number = atoi(str.c_str());
		stk.push(number);
		return;
	}
	else
	{
		GetChar(inps);
		GetExpression(inps);
		GetChar(inps);
	}
}

void Expression::GetTerm(fstream& inps)
{
	char factOp;
	int num, num1, num2;

	GetFactor(inps);

	while (ch == '*' || ch == '/' || ch == '^')
	{
		factOp = ch;

		GetChar(inps);
		GetFactor(inps);

		num2 = stk.top();
		stk.pop();
		num1 = stk.top();
		stk.pop();

		if (factOp == '*')
			num = num1 * num2;
		else if (factOp == '/')
			num = num1 / num2;
		else if (factOp == '^')
			num = (int)pow(num1, num2);

		stk.push(num);
	}
}

#include "pch.h"
#include "Expression.h"
#include <fstream>
#include <iostream>
using namespace std;

int main()
{
    bool validExp;
    int expVal;
    fstream inps;
    Expression ex;

    inps.open("TestExp.txt", fstream::in);
    
    if (!inps.eof())
    {
        validExp = true;
        ex.GetChar(inps);
        ex.GetExpression(inps);
        expVal = ex.stk.top();
        ex.stk.pop();
        cout << "Value = " << expVal << endl;
    }

    else
    {
        validExp = false;
        expVal = 0;
    }

    return 0;
}