Category: C# Computer Programming Language
C# Three-Dimensional Cartesian Vector Calculator (c) September 24, 2023, by James Pate Williams, Jr. All Applicable Rights Reserved
I wrote and debugged this C# code after I found out that my 1989 vector calculator in Modula-2 for the Commadore Amiga 2000 was not working correctly.
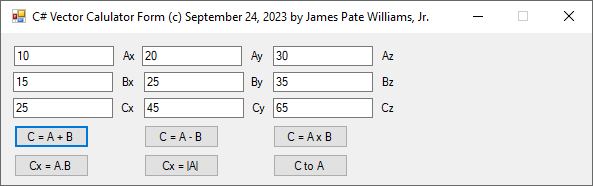
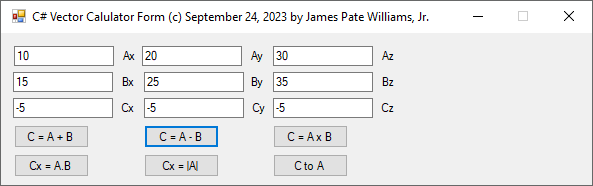
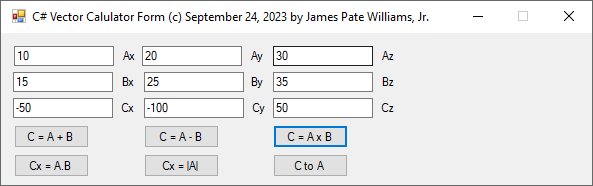
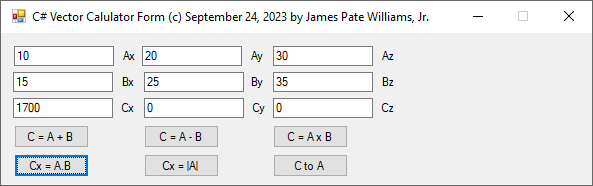
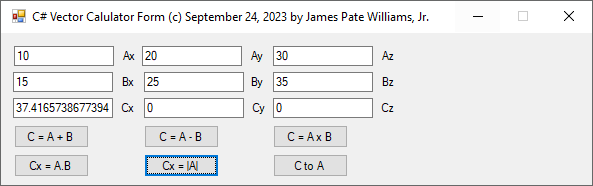

// C# Three-Dimensional Cartesian Vector Calculator
// (c) September 24, 2023 by James Pate Williams, Jr.
// All Applicable Rights Reserved
using System;
using System.Windows.Forms;
namespace CSVectorCalculator
{
public partial class MainForm : Form
{
public MainForm()
{
InitializeComponent();
}
private static double[] A = new double[3];
private static double[] B = new double[3];
private static double[] C = new double[3];
private void ValidateAB(
ref bool valid)
{
try
{
A[0] = double.Parse(textBox1.Text);
A[1] = double.Parse(textBox2.Text);
A[2] = double.Parse(textBox3.Text);
B[0] = double.Parse(textBox4.Text);
B[1] = double.Parse(textBox5.Text);
B[2] = double.Parse(textBox6.Text);
valid = true;
}
catch (Exception ex)
{
MessageBox.Show(ex.Message, "Warning",
MessageBoxButtons.OK, MessageBoxIcon.Warning);
valid = false;
}
}
private void FillC(double[] C)
{
textBox7.Text = C[0].ToString();
textBox8.Text = C[1].ToString();
textBox9.Text = C[2].ToString();
}
private void button1_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] + B[0];
C[1] = A[1] + B[1];
C[2] = A[2] + B[2];
FillC(C);
}
}
private void button2_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] - B[0];
C[1] = A[1] - B[1];
C[2] = A[2] - B[2];
FillC(C);
}
}
private void button3_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[1] * B[2] - A[2] * B[1];
C[1] = A[0] * B[2] - A[2] * B[0];
C[2] = A[1] * B[0] - A[0] * B[1];
FillC(C);
}
}
private void button4_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] * B[0] + A[1] * B[1] + A[2] * B[2];
C[1] = C[2] = 0.0;
FillC(C);
}
}
private void button5_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = Math.Sqrt(A[0] * A[0] + A[1] * A[1] + A[2] * A[2]);
C[1] = C[2] = 0.0;
FillC(C);
}
}
private void button6_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
textBox1.Text = C[0].ToString();
textBox2.Text = C[1].ToString();
textBox3.Text = C[2].ToString();
C[0] = C[1] = C[2] = 0.0;
FillC(C);
}
}
}
}
Two of Kepler’s Three Laws of Planetary Motion by James Pate Williams, Jr.
Comparison of Aitkin Extrapolation and Newton’s Method to Compute Square Roots by James Pate Williams, Jr.
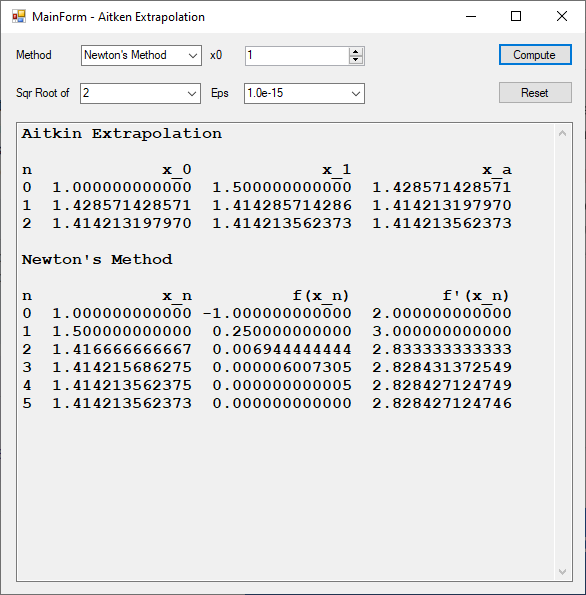

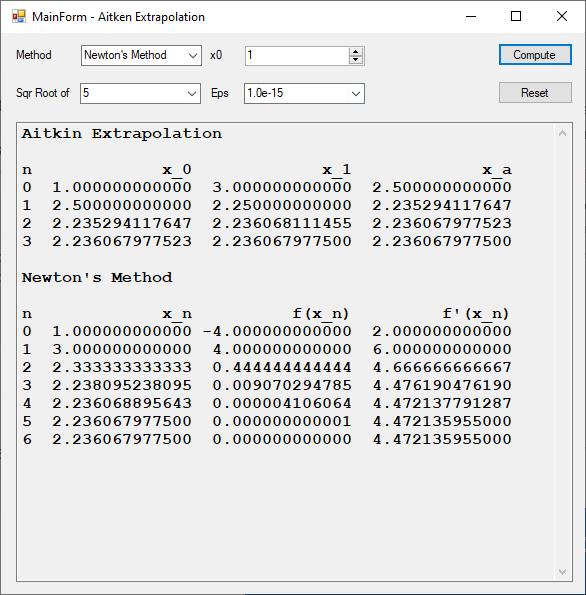

Comparison of Linear Systems Applications in C# and C++ by James Pate Williams, Jr.
Back in 2017 I created a C# application that implemented the direct methods: Cholesky decomposition, Gaussian elimination with partial pivoting, LU decomposition, and simple Gaussian elimination. The classical iterative methods Gauss-Seidel, Jacobi, Successive Overrelaxation, and gradient descent were also implemented along with the modern iterative methods: conjugate gradient descent and Modified Richardson’s method. Recently I translated the C# code to C++. I used the following test matrices: Cauchy, Lehmer, Pascal, and other. Below are some results. As is apparent the C++ runtimes are faster than the C# execution times.
Richardson Method Translated from C Source Code to C# by James Pate Williams, Jr.


The Richardson Method is called before eliminating the system of linear equations.
Added elimination results from a vanilla C program and a C# application.


These results are not in total agreement with H. T. Lau’s results.
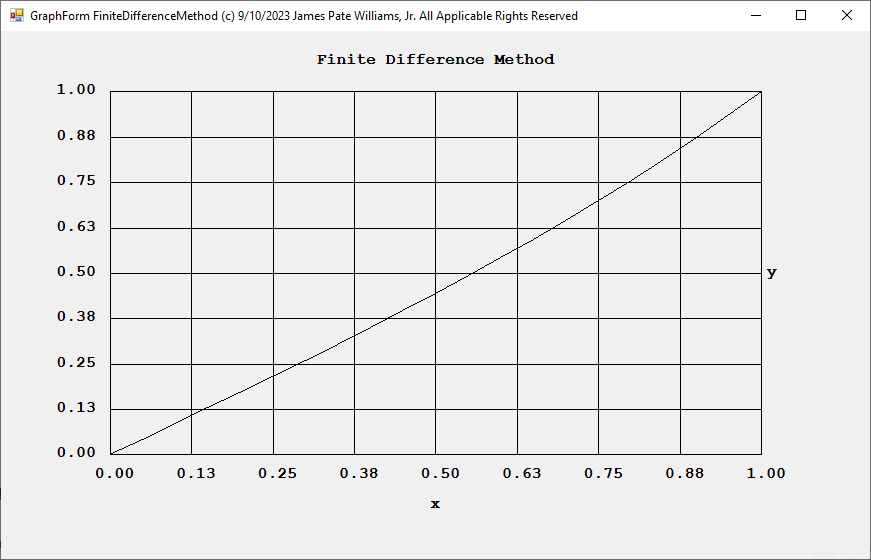
Finite Difference Method for Solving Second Order Ordinary Differential Equations by James Pate Williams, Jr.
My reference is Numerical Analysis: An Algorithmic Approach 3rd Edition by S. D. Conte and Carl de Boor Chapter 9.1.
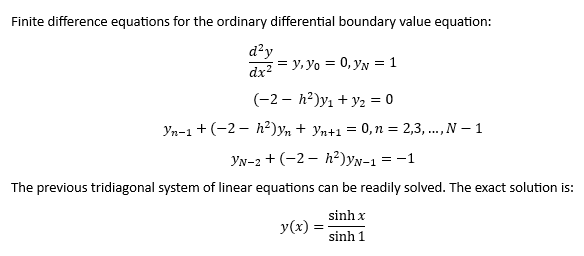


Estimated Babe Ruth 1921 Homerun Parameters by James Pate Williams, Jr.
“Babe Ruth is generally considered the owner of the record for the longest home run in MLB history with a 575-foot bomb launched at Navin Field in Detroit in 1921.” – https://www.msn.com/en-us/sports/mlb/what-is-the-longest-home-run-in-mlb-history/ar-AA1dGwlZ
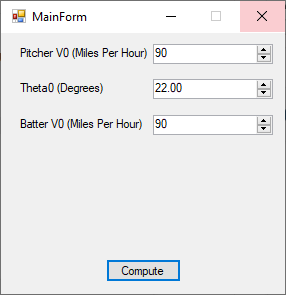
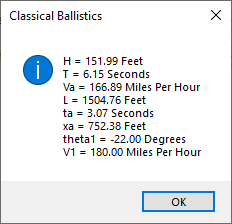
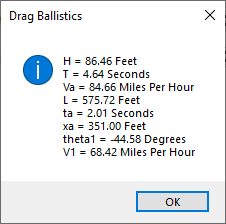
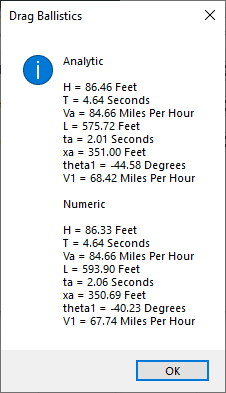
As you can see, I estimated the pitch velocity at 90 miles per hour and Babe Ruth’s (Sultan of Swing) at 90 miles per hour also. My analytic calculations yield a range of the baseball’s trajectory as about 576 feet.
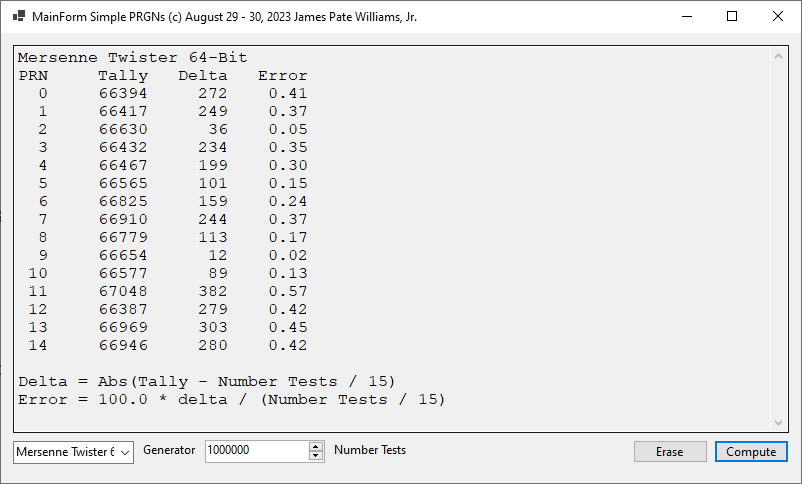
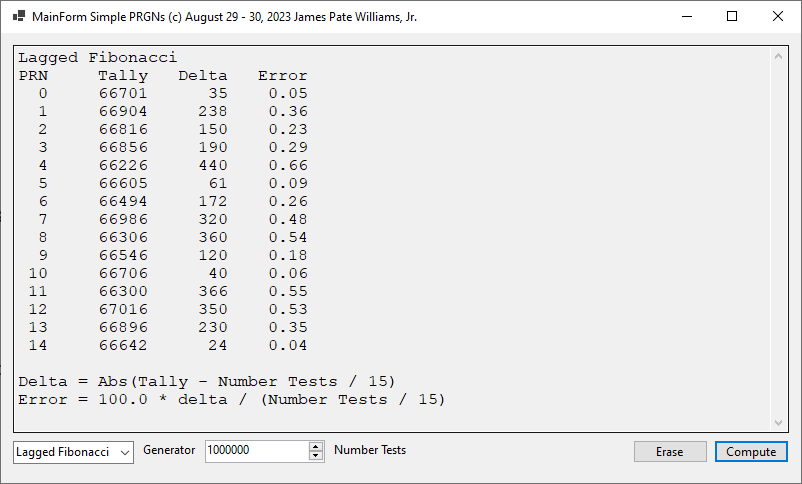
Added the Pseudo-Random Number Generators: Mersenne Twister and Lagged Fibonacci to My C# Application by James Pate Wiliams, Jr. with the Help of the Internet
// "Numerical Computation 2: Methods, Software,
// and Analysis" by Christoph W. Ueberhuber
// Chapter 17 Random Numbers
// "The Art of Computer Programming Volume 2"
// "Seminumerical Algorithms Second Edition"
// "Chapter 3 RANDOM NUMBERS" by Donald E. Knuth
// https://en.wikipedia.org/wiki/Mersenne_Twister
using System.Collections.Generic;
namespace SimplePRNGs
{
class PRNGs
{
private long AMxn1, AMxn;
private long AMyn1, AMyn;
private long AMk;
private long AMm = 34359738368;
private long LCG0z0, LCG0z1;
private long LCG1z0, LCG1z1;
private long LCG2z0, LCG2z1, LCG2z2;
private long MFG0z0, MFG0z1;
private readonly long LCG0m = 4294967296;
private readonly long LCG2m = 2147483647;
private readonly List<long> AMV = new();
private long MTindex;
private long[] MT;
private LaggedFibRng fibRng;
public void SetSeedLCG0(long z0)
{
LCG0z0 = z0;
}
public void SetSeedLCG1(long z0)
{
LCG1z0 = z0;
}
public void SetSeedLCG2(long z0, long z1)
{
LCG2z0 = z0;
LCG2z1 = z1;
}
public long LCG0()
{
LCG0z1 = (69069 * LCG0z0) % LCG0m;
LCG0z0 = LCG0z1;
return LCG0z1;
}
public long LCG1()
{
LCG1z1 = (69069 * LCG1z0 + 1) % LCG0m;
LCG1z0 = LCG1z1;
return LCG1z1;
}
public long LCG2()
{
LCG2z2 = (1999 * LCG2z1 + 4444 * LCG2z0) % LCG2m;
LCG2z0 = LCG2z1;
LCG2z1 = LCG2z2;
return LCG2z2;
}
public void SetSeedMFG0(long z0, long z1)
{
MFG0z0 = z0;
MFG0z1 = z1;
}
public long MFG0()
{
long MFG0z2 = (MFG0z1 + MFG0z0) % LCG0m;
MFG0z0 = MFG0z1;
MFG0z1 = MFG0z2;
return MFG0z2;
}
public void ComputeNextXY()
{
AMxn1 = (3141592653 * AMxn + 2718281829) % AMm;
if (AMxn1 < 0)
AMxn1 += AMm;
AMyn1 = (2718281829 * AMyn + 3141592653) % AMm;
if (AMyn1 < 0)
AMyn1 += AMm;
}
public void AMSeed(long k, long x0, long y0)
{
long AMTxn1, AMTxn = x0;
AMxn = x0;
AMyn = y0;
AMk = k;
for (int i = 0; i < k; i++)
{
AMTxn1 = (3141592653 * AMTxn + 2718281829) % AMm;
if (AMTxn1 < 0)
AMTxn1 += AMm;
AMTxn = AMTxn1;
AMV.Add(AMTxn1);
}
}
public long AlgorithmM()
{
ComputeNextXY();
AMxn = AMxn1;
AMyn = AMyn1;
long j = (AMk * AMyn1) / AMm;
long r = AMV[(int)j];
AMV[(int)j] = AMxn1;
if (r < 0)
r += AMm;
return r;
}
public void MTInitialization(long seed)
{
long f = 6364136223846793005;
long n = 312, w = 64;
MTindex = n;
MT = new long[n];
MT[0] = seed;
for (int i = 1; i < n; i++)
MT[i] = f * (MT[i - 1] ^ (MT[i - 1] >> (int)(w - 2))) + i;
}
public long MTExtractNumber()
{
unchecked
{
long n = 312;
long c = (long)0xFFF7EEE000000000;
long b = 0x71D67FFFEDA60000;
long d = 0x5555555555555555;
long u = 29, s = 17, t = 27, l = 43;
if (MTindex == n)
MTTwist();
long y = MT[MTindex];
y ^= ((y >> (int)u) & d);
y ^= ((y << (int)s) & b);
y ^= ((y << (int)t) & c);
y ^= (y >> (int)l);
MTindex++;
return y;
}
}
public void MTTwist()
{
unchecked
{
long n = 312, m = 156, r = 31;
long a = (long)0xB5026F5AA96619E9;
MTindex = n + 1;
long lower_mask = (1 << (int)r) - 1;
long upper_mask = ~lower_mask;
for (int i = 0; i < n; i++)
{
long x = (MT[i] & upper_mask) |
(MT[(i + 1) % n] & lower_mask);
long xA = x >> 1;
if (x % 2 != 0)
xA ^= a;
MT[i] = MT[(i + m) % n] ^ xA;
}
}
MTindex = 0;
}
public void LaggedFibRngSeed(int seed)
{
fibRng = new LaggedFibRng(seed);
}
public long LaggedFibonacci(long modulus)
{
long lo = fibRng.Next();
long hi = fibRng.Next();
long rs = ((hi << 31) | lo) % modulus;
return rs;
}
}
}
//https://learn.microsoft.com/en-us/archive/msdn-magazine/2016/august/test-run-lightweight-random-number-generation
// modified by current author James Pate Williams, Jr. on August 30, 2023
using System.Collections.Generic;
namespace SimplePRNGs
{
public class LaggedFibRng
{
private const int k = 606; // Largest magnitude"-index"
private const int j = 273; // Other "-index"
private const long m = 4294967296; // 2^32
private readonly List<long> vals = null;
private long seed;
public LaggedFibRng(int seed)
{
vals = new List<long>();
for (int i = 0; i < k + 1; ++i)
vals.Add(i);
if (seed % 2 == 0) vals[0] = 11;
// Burn some values away
for (int ct = 0; ct < 1000; ++ct)
{
long dummy = Next();
}
} // ctor
public long Next()
{
// (a + b) mod n = [(a mod n) + (b mod n)] mod n
long left = vals[0] % m; // [x-big]
long right = vals[k - j] % m; // [x-other]
long sum = (left + right) % m; // prevent overflow
if (sum < 0)
seed = sum + m;
else
seed = sum;
vals.Insert(k + 1, seed); // Add new val at end
vals.RemoveAt(0); // Delete now irrelevant [0] val
return seed;
}
}
}
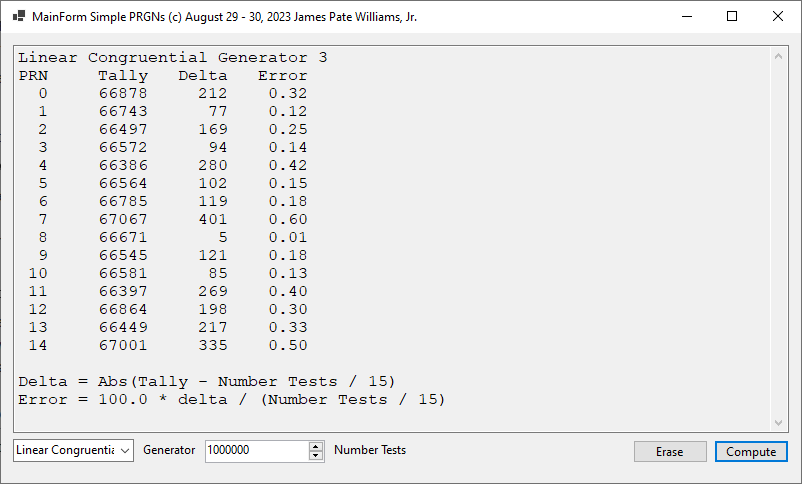
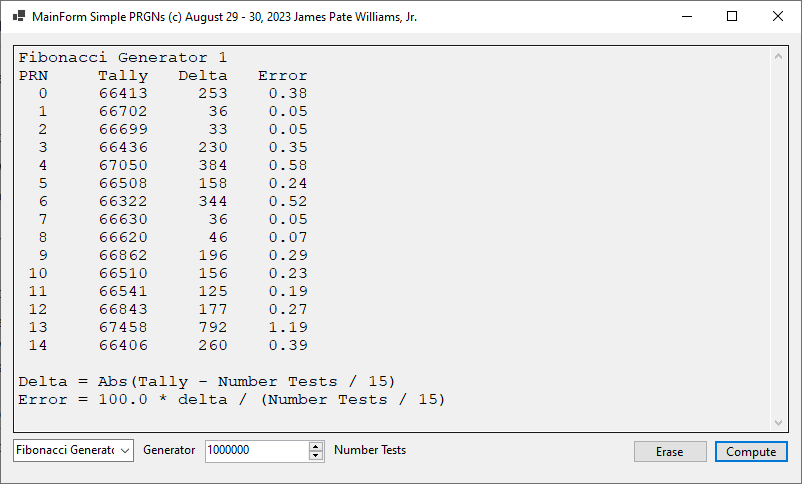
Simple Pseudo-Random Number Generators in C# Implemented by James Pate Williams, Jr.



// "Numerical Computation 2: Methods, Software,
// and Analysis" by Christoph W. Ueberhuber
// Chapter 17 Random Numbers
// "The Art of Computer Programming Volume 2"
// "Seminumerical Algorithms Second Edition"
// "Chapter 3 RANDOM NUMBERS" by Donald E. Knuth
using System.Collections.Generic;
namespace SimplePRNGs
{
class PRNGs
{
private long AMxn1, AMxn;
private long AMyn1, AMyn;
private long AMk;
private long AMm = 34359738368;
private long LCG0z0, LCG0z1;
private long LCG1z0, LCG1z1;
private long LCG2z0, LCG2z1, LCG2z2;
private long MFG0z0, MFG0z1;
private readonly long LCG0m = 4294967296;
private readonly long LCG2m = 2147483647;
private readonly List<long> AMV = new();
public void SetSeedLCG0(long z0)
{
LCG0z0 = z0;
}
public void SetSeedLCG1(long z0)
{
LCG1z0 = z0;
}
public void SetSeedLCG2(long z0, long z1)
{
LCG2z0 = z0;
LCG2z1 = z1;
}
public long LCG0()
{
LCG0z1 = (69069 * LCG0z0) % LCG0m;
LCG0z0 = LCG0z1;
return LCG0z1;
}
public long LCG1()
{
LCG1z1 = (69069 * LCG1z0 + 1) % LCG0m;
LCG1z0 = LCG1z1;
return LCG1z1;
}
public long LCG2()
{
LCG2z2 = (1999 * LCG2z1 + 4444 * LCG2z0) % LCG2m;
LCG2z0 = LCG2z1;
LCG2z1 = LCG2z2;
return LCG2z2;
}
public void SetSeedMFG0(long z0, long z1)
{
MFG0z0 = z0;
MFG0z1 = z1;
}
public long MFG0()
{
long MFG0z2 = (MFG0z1 + MFG0z0) % LCG0m;
MFG0z0 = MFG0z1;
MFG0z1 = MFG0z2;
return MFG0z2;
}
public void ComputeNextXY()
{
AMxn1 = (3141592653 * AMxn + 2718281829) % AMm;
if (AMxn1 < 0)
AMxn1 += AMm;
AMyn1 = (2718281829 * AMyn + 3141592653) % AMm;
if (AMyn1 < 0)
AMyn1 += AMm;
}
public void AMSeed(long k, long x0, long y0)
{
long AMTxn1, AMTxn = x0;
AMxn = x0;
AMyn = y0;
AMk = k;
for (int i = 0; i < k; i++)
{
AMTxn1 = (3141592653 * AMTxn + 2718281829) % AMm;
if (AMTxn1 < 0)
AMTxn1 += AMm;
AMTxn = AMTxn1;
AMV.Add(AMTxn1);
}
}
public long AlgorithmM()
{
ComputeNextXY();
AMxn = AMxn1;
AMyn = AMyn1;
long j = (AMk * AMyn1) / AMm;
long r = AMV[(int)j];
AMV[(int)j] = AMxn1;
if (r < 0)
r += AMm;
return r;
}
}
}