See the following website for the used algorithms pages 119 to 121:


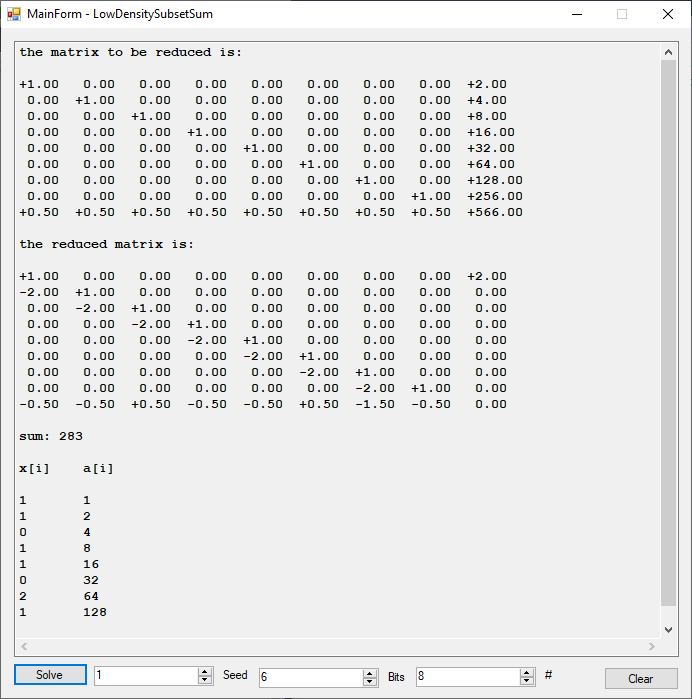



See the following website for the used algorithms pages 119 to 121:






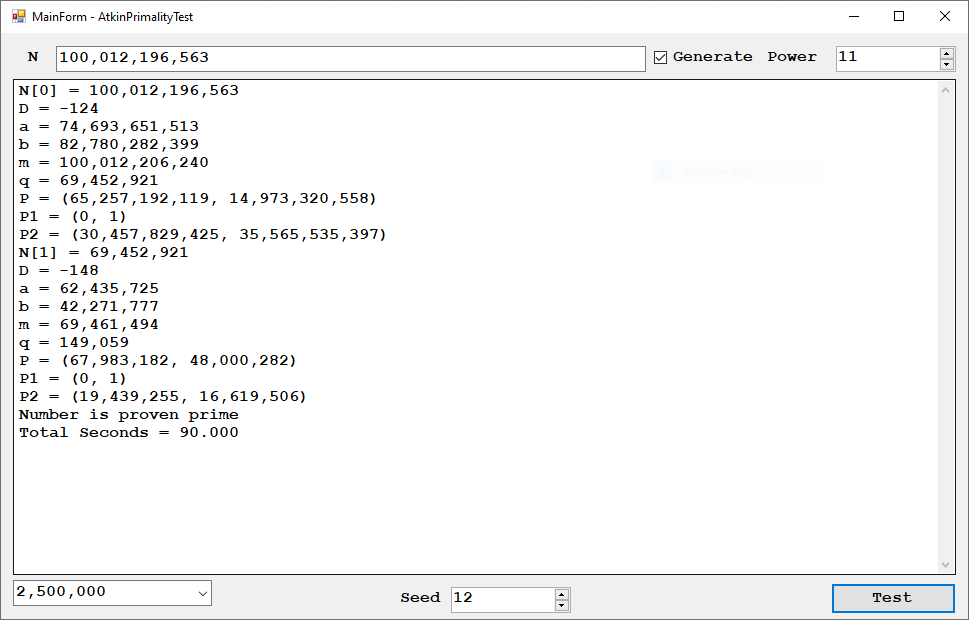
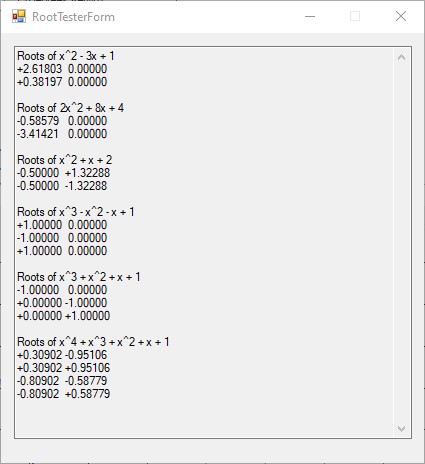
Back in 2022 I reimplemented Henri Cohen’s Atkin’s Primality Test algorithm. This test makes use of an elliptic curve analog of Pocklington’s theorem. I restate the theorem utilized from Henri Cohen’s “A course in Computational Algebraic Number Theory” on pages 467 to 468: “Proposition 9.2.1. Let N be an integer coprime to 6 and different from 1, and E be an elliptic curve modulo N. Assume that we know an integer m a point P contained on the elliptic curve satisfying the following conditions. (1) There exists a prime divisor q of m such that q > (N^1/4 + 1) ^ 2 (2) m * P = O_E = (0 : 1 : ). (3) (m / q) * P = (x : y : t) with t contained in (Z/NZ)*. Then N is prime.” I used C# and Microsoft’s BigInteger class. I have not been able to prove numbers greater than 14 decimal digits to be prime. I am recoding the algorithm in C++ which limits me to 19 decimal digits since 2 ^ 63 – 1 = 9,223,372,036,854,775,807 (Int64).




We use two numerical analysis algorithms and two artificial intelligent methods. The first two techniques are from the excellent tome “A Numerical Library in C for Scientists and Engineers” by H.T. Lau, PhD. One does not utilize any derivatives and the other requires first partial derivatives. My homegrown algorithms are my implementation of the particle swarm optimization and an evolutionary hill-climber. The output from my C# application is below:
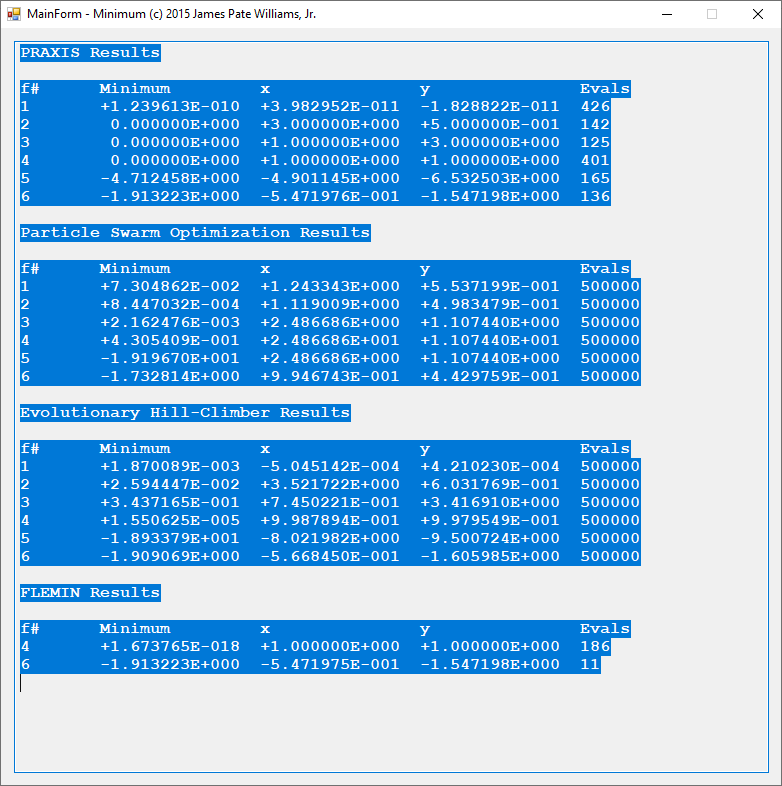
The two numerical algorithms PRAXIS and FLEMIN perform fairly well and do not require that many function evaluations which is better metric than wall-clock time.
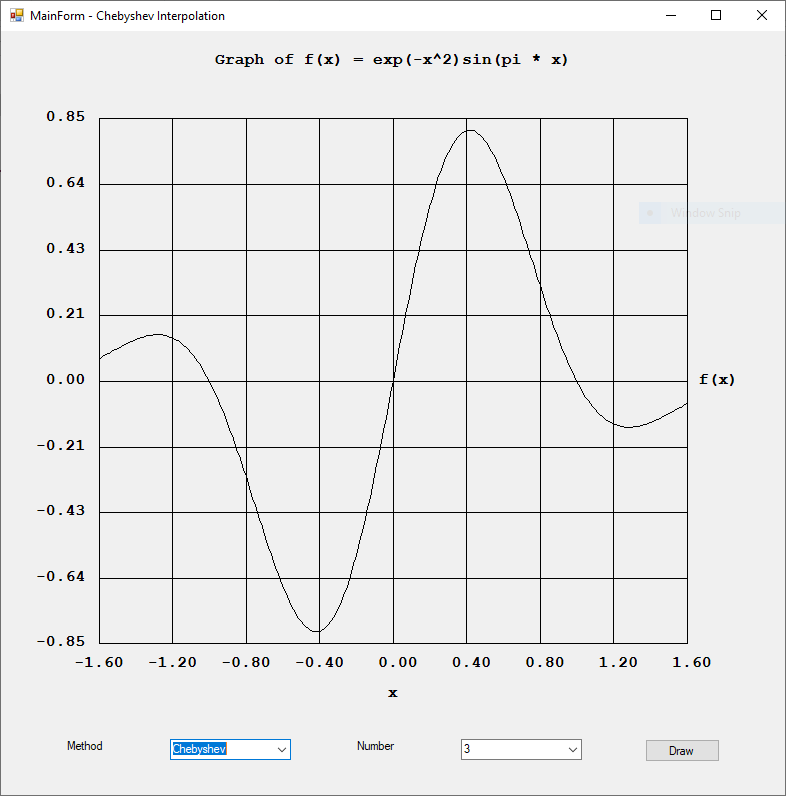
See the excellent webpage: https://en.wikipedia.org/wiki/Test_functions_for_optimization
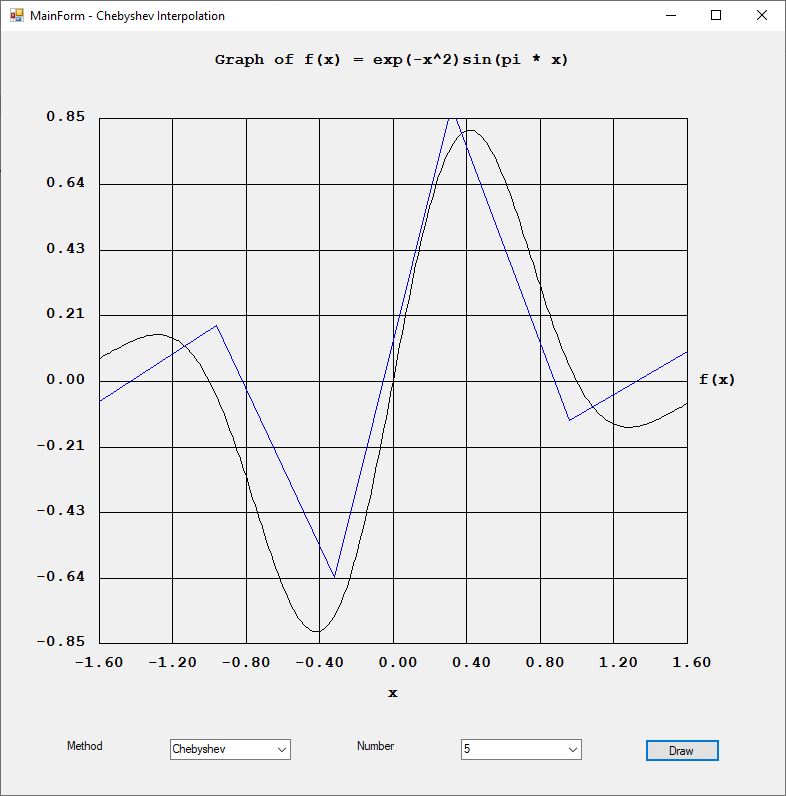
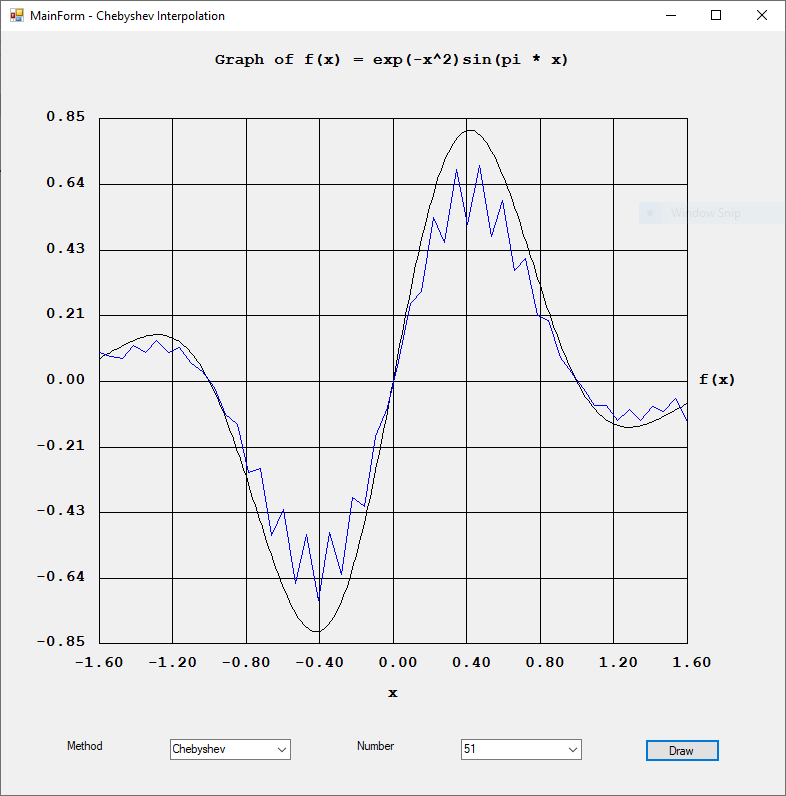
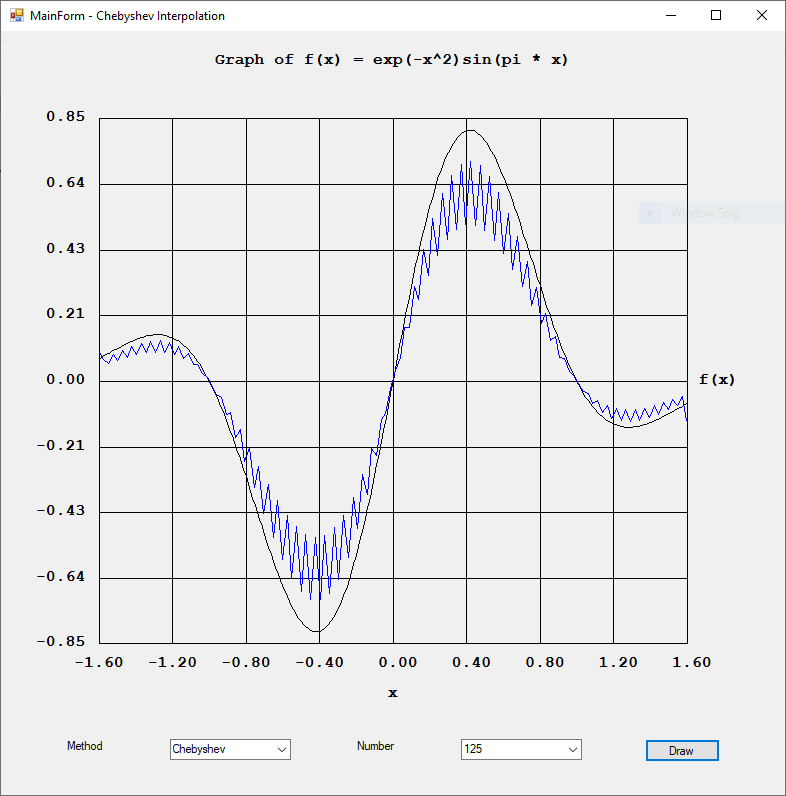
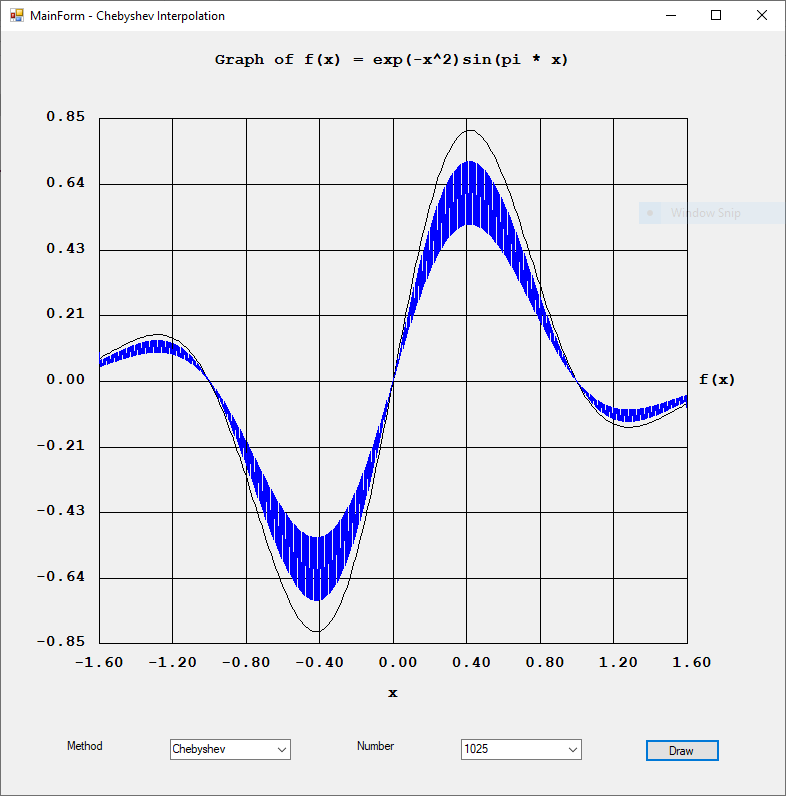
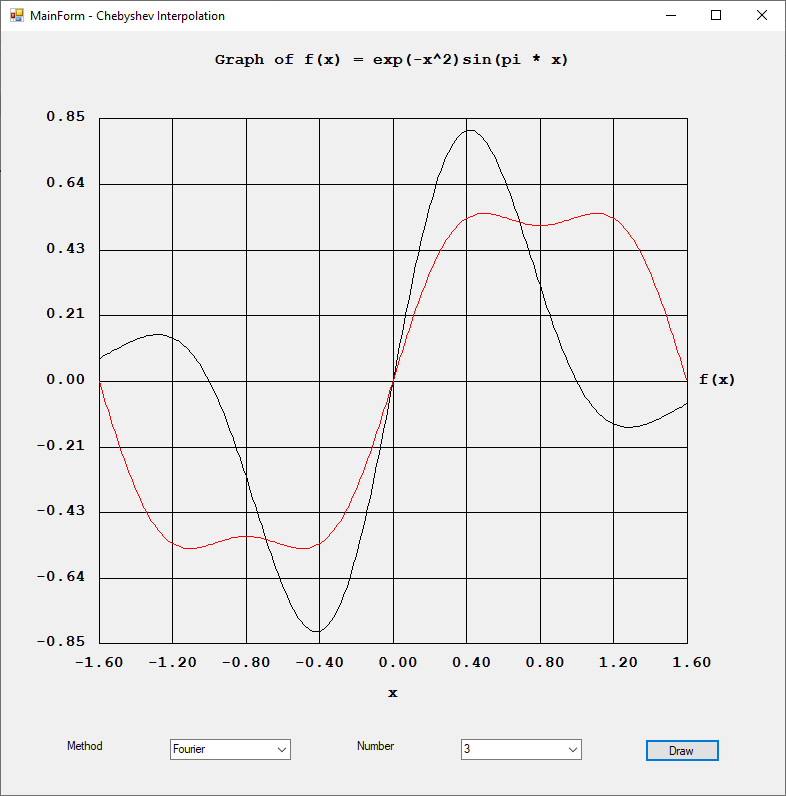

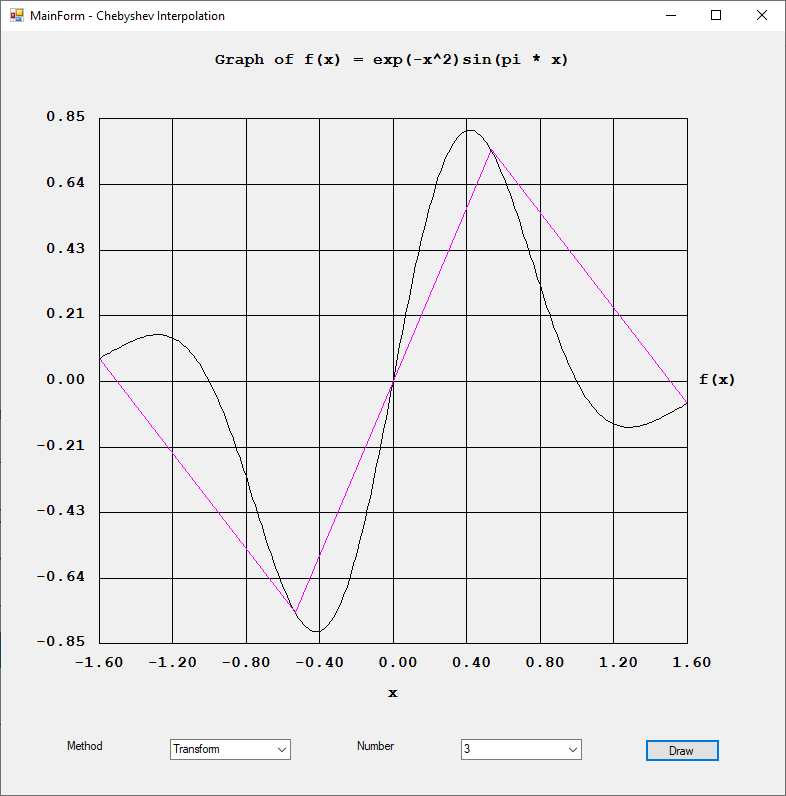

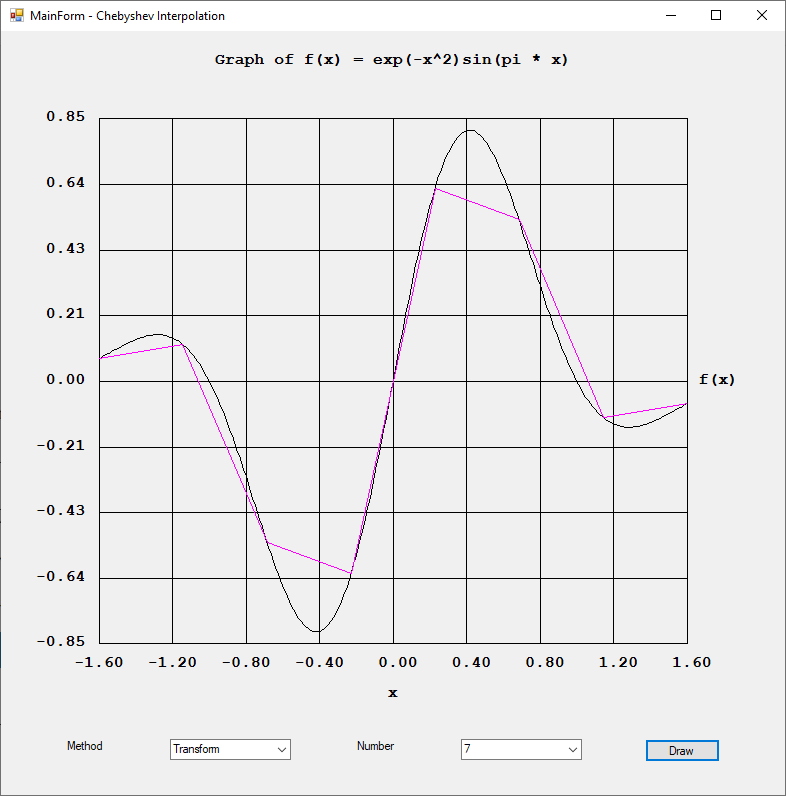
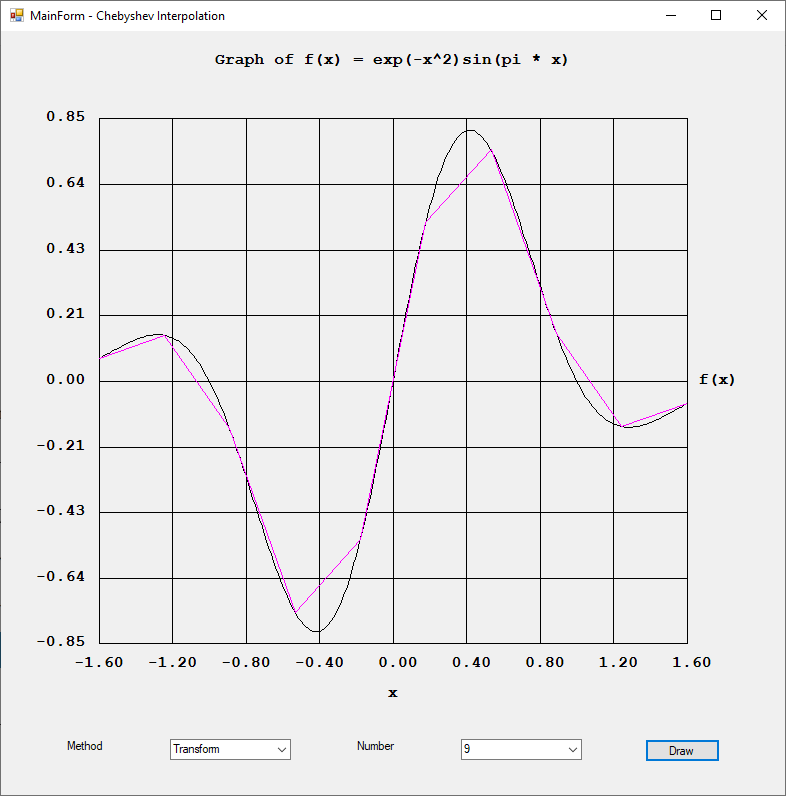

Rexx was a popular computer programming language on IBM main frame computers. I found an interesting website: https://en.wikipedia.org/wiki/Rexx#NUMERIC\
I use a very slowly converging infinite series and Fourier series to compute Pi.

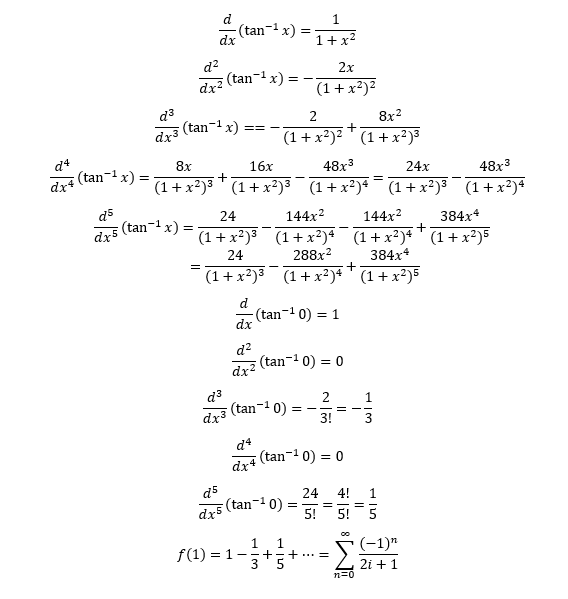



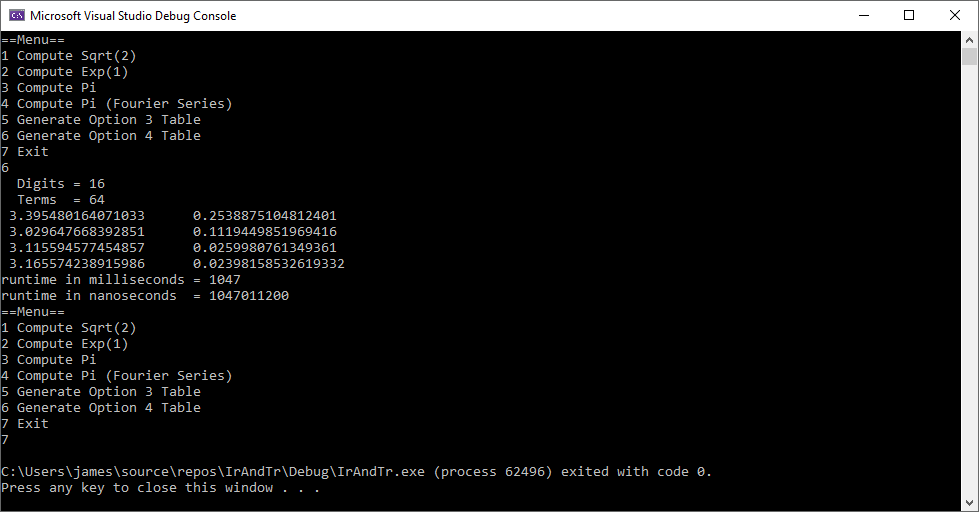
// https://en.wikipedia.org/wiki/Rexx#NUMERIC\
// Translated from Rexx code
// by James Pate Williams, Jr.
// Added a lot of functionality
// Copyrighted February 7 - 10, 2023
#include "FourierSeries.h"
#include <stdlib.h>
#include <iomanip>
#include <iostream>
#include <chrono>
using namespace std;
typedef chrono::high_resolution_clock Clock;
void Option3(int digits, int N)
{
long double i = 0;
long double sgn = 1;
long double sum = 0;
long double pi0 = Pi;
long double pi1 = 0.0;
while (i <= N)
{
sum += sgn / (2.0 * i + 1);
sgn *= -1;
i = i + 1.0;
}
pi1 = 4.0 * sum;
cout << setw(static_cast<std::streamsize>((int)digits) + 2);
cout << setprecision(digits) << pi1 << '\t';
cout << setprecision(digits) << (fabsl(pi0 - pi1)) << endl;
}
void Option4(int digits, int N)
{
long double* a = new long double[N + 1];
long double* b = new long double[N + 1];
memset(a, 0, (N + 1) * sizeof(long double));
memset(b, 0, (N + 1) * sizeof(long double));
FourierSeries::CreateCosSeries(N, a);
FourierSeries::CreateSinSeries(N, b);
long double pi = 4.0 * FourierSeries::Series(N, 1.0, a, b);
cout << setw(static_cast<std::streamsize>((int)digits) + 2);
cout << setprecision(digits) << pi << '\t';
cout << setprecision(digits) << (fabsl(pi - Pi)) << endl;
delete[] a;
delete[] b;
}
int main()
{
int choice, digits, N = 0, N1 = 0;
while (1)
{
cout << "==Menu==" << endl;
cout << "1 Compute Sqrt(2)" << endl;
cout << "2 Compute Exp(1)" << endl;
cout << "3 Compute Pi" << endl;
cout << "4 Compute Pi (Fourier Series)" << endl;
cout << "5 Generate Option 3 Table" << endl;
cout << "6 Generate Option 4 Table" << endl;
cout << "7 Exit" << endl;
cin >> choice;
if (choice == 7)
break;
cout << " Digits = ";
cin >> digits;
if (choice >= 3)
{
cout << " Terms = ";
cin >> N;
N1 = N + 1;
}
auto start_time = Clock::now();
if (choice == 1)
{
long double n = 2;
long double r = 1;
while (1)
{
long double rr = (n / r + r) / 2;
if (rr == r)
break;
r = rr;
}
cout << setprecision(digits) << r << endl;
}
else if (choice == 2)
{
long double e = 2.5;
long double f = 0.5;
long double n = 3;
do
{
f /= n;
long double ee = e + f;
if (ee == e)
break;
e = ee;
n += 1;
} while (1);
cout << setprecision(digits) << e << endl;
}
else if (choice == 3)
Option3(digits, N);
else if (choice == 4)
Option4(digits, N);
else if (choice == 5)
{
for (int n = 8; n <= N; n *= 2)
Option3(digits, n);
}
else if (choice == 6)
{
for (int n = 8; n <= N; n *= 2)
Option4(digits, n);
}
auto end_time = Clock::now();
cout << "runtime in milliseconds = ";
cout << std::chrono::duration_cast<std::chrono::milliseconds>
(end_time - start_time).count();
cout << endl;
cout << "runtime in nanoseconds = ";
cout << std::chrono::duration_cast<std::chrono::nanoseconds>
(end_time - start_time).count();
cout << endl;
}
return 0;
}
#pragma once
const long double c = 2.0e9;
const long double Pi = 3.1415926535897932384626433832795;
class FourierSeries
{
private:
static long double f(long double x);
static long double cosTermFunction(int n, long double x);
static long double sinTermFunction(int n, long double x);
public:
static void CreateCosSeries(int N, long double a[]);
static void CreateSinSeries(int N, long double b[]);
static long double Series(int N, long double x,
long double a[], long double b[]);
};
#include <math.h>
#include "FourierSeries.h"
#include "Integral.h"
long double FourierSeries::f(long double x)
{
return atanl(x);
}
long double FourierSeries::cosTermFunction(int n, long double x)
{
return cosl(n * x * Pi / c) * f(x);
}
long double FourierSeries::sinTermFunction(int n, long double x)
{
return sinl(n * x * Pi / c) * f(x);
}
void FourierSeries::CreateCosSeries(int N, long double a[])
{
long double e[7] = { 0 };
e[1] = e[2] = 1.0e-12;
for (int n = 0; n <= N; n++)
a[n] = Integral::integral(
n, -c, c, cosTermFunction, e, 1, 1) / c;
}
void FourierSeries::CreateSinSeries(int N, long double b[])
{
long double e[7] = { 0 };
e[1] = e[2] = 1.0e-12;
for (int n = 1; n <= N; n++)
b[n] = Integral::integral(
n, -c, c, sinTermFunction, e, 1, 1) / c;
}
long double FourierSeries::Series(int N, long double x,
long double a[], long double b[])
{
long double sum = 0.0;
for (int n = 1; n <= N; n++)
sum += a[n] * cosl(2.0 * n * x) + b[n] * sinl(2.0 * n * x);
return a[0] / 2.0 + sum / 2.0;
}
#pragma once
// Translated from C source code found in the tome
// "A Numerical Library in C for Scientists and
// Engineers" by H.T. Lau, PhD
class Integral
{
private:
static long double integralqad(
int n,
int transf, long double (*fx)(int, long double), long double e[],
long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
long double* f2, long double re, long double ae, long double b1);
static void integralint(
int n,
int transf, long double (*fx)(int, long double), long double e[],
long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
long double* f2, long double* sum, long double re, long double ae, long double b1,
long double hmin);
public:
static long double integral(int n, long double a, long double b,
long double (*fx)(int, long double), long double e[],
int ua, int ub);
};
#include <math.h>
#include "Integral.h"
long double Integral::integral(
int n,
long double a, long double b,
long double (*fx)(int, long double), long double e[],
int ua, int ub)
{
long double x0, x1, x2, f0, f1, f2, re, ae, b1 = 0, x;
re = e[1];
if (ub)
ae = e[2] * 180.0 / fabsl(b - a);
else
ae = e[2] * 90.0 / fabsl(b - a);
if (ua) {
e[3] = e[4] = 0.0;
x = x0 = a;
f0 = (*fx)(n, x);
}
else {
x = x0 = a = e[5];
f0 = e[6];
}
e[5] = x = x2 = b;
e[6] = f2 = (*fx)(n, x);
e[4] += integralqad(n, 0, fx, e, &x0, &x1, &x2, &f0, &f1, &f2, re, ae, b1);
if (!ub) {
if (a < b) {
b1 = b - 1.0;
x0 = 1.0;
}
else {
b1 = b + 1.0;
x0 = -1.0;
}
f0 = e[6];
e[5] = x2 = 0.0;
e[6] = f2 = 0.0;
ae = e[2] * 90.0;
e[4] -= integralqad(n, 1, fx, e, &x0, &x1, &x2, &f0, &f1, &f2, re, ae, b1);
}
return e[4];
}
long double Integral::integralqad(
int n,
int transf, long double (*fx)(int, long double), long double e[],
long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
long double* f2, long double re, long double ae, long double b1)
{
/* this function is internally used by INTEGRAL */
long double sum, hmin, x, z;
hmin = fabs((*x0) - (*x2)) * re;
x = (*x1) = ((*x0) + (*x2)) * 0.5;
if (transf) {
z = 1.0 / x;
x = z + b1;
(*f1) = (*fx)(n, x) * z * z;
}
else
(*f1) = (*fx)(n, x);
sum = 0.0;
integralint(n, transf, fx, e, x0, x1, x2, f0, f1, f2, &sum, re, ae, b1, hmin);
return sum / 180.0;
}
void Integral::integralint(
int n,
int transf, long double (*fx)(int, long double), long double e[],
long double* x0, long double* x1, long double* x2, long double* f0, long double* f1,
long double* f2, long double* sum, long double re, long double ae, long double b1,
long double hmin)
{
/* this function is internally used by INTEGRALQAD of INTEGRAL */
int anew;
long double x3, x4, f3, f4, h, x, z, v, t;
x4 = (*x2);
(*x2) = (*x1);
f4 = (*f2);
(*f2) = (*f1);
anew = 1;
while (anew) {
anew = 0;
x = (*x1) = ((*x0) + (*x2)) * 0.5;
if (transf) {
z = 1.0 / x;
x = z + b1;
(*f1) = (*fx)(n, x) * z * z;
}
else
(*f1) = (*fx)(n, x);
x = x3 = ((*x2) + x4) * 0.5;
if (transf) {
z = 1.0 / x;
x = z + b1;
f3 = (*fx)(n, x) * z * z;
}
else
f3 = (*fx)(n, x);
h = x4 - (*x0);
v = (4.0 * ((*f1) + f3) + 2.0 * (*f2) + (*f0) + f4) * 15.0;
t = 6.0 * (*f2) - 4.0 * ((*f1) + f3) + (*f0) + f4;
if (fabsl(t) < fabsl(v) * re + ae)
(*sum) += (v - t) * h;
else if (fabsl(h) < hmin)
e[3] += 1.0;
else {
integralint(n, transf, fx, e, x0, x1, x2, f0, f1, f2, sum,
re, ae, b1, hmin);
*x2 = x3;
*f2 = f3;
anew = 1;
}
if (!anew) {
*x0 = x4;
*f0 = f4;
}
}
}
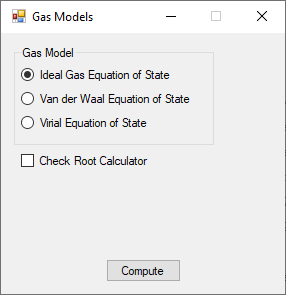
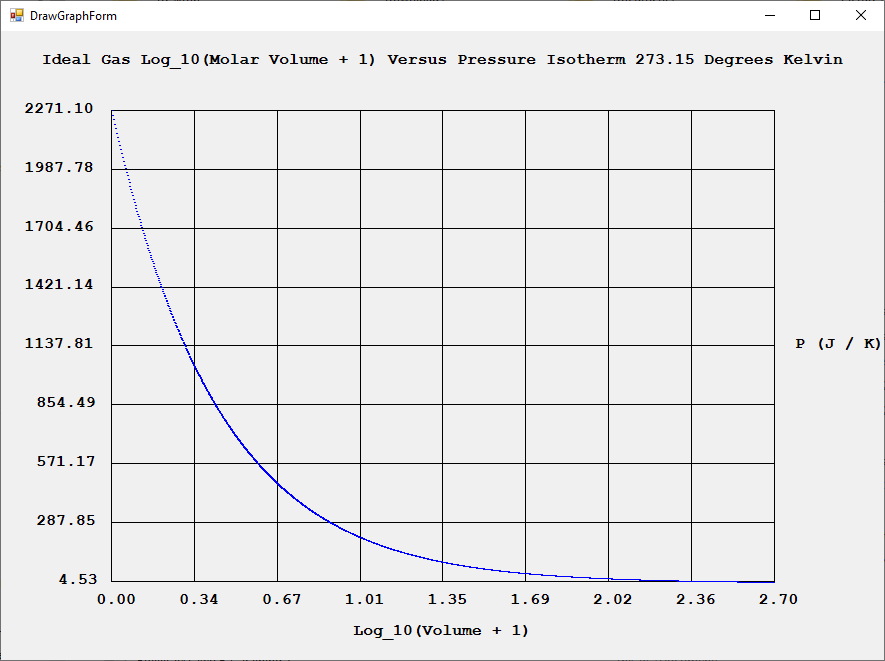
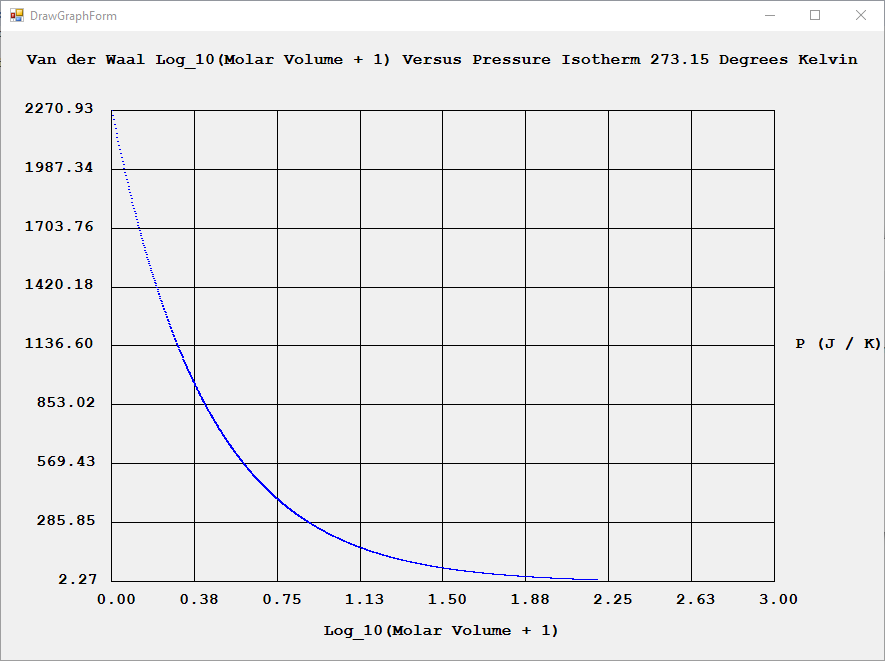
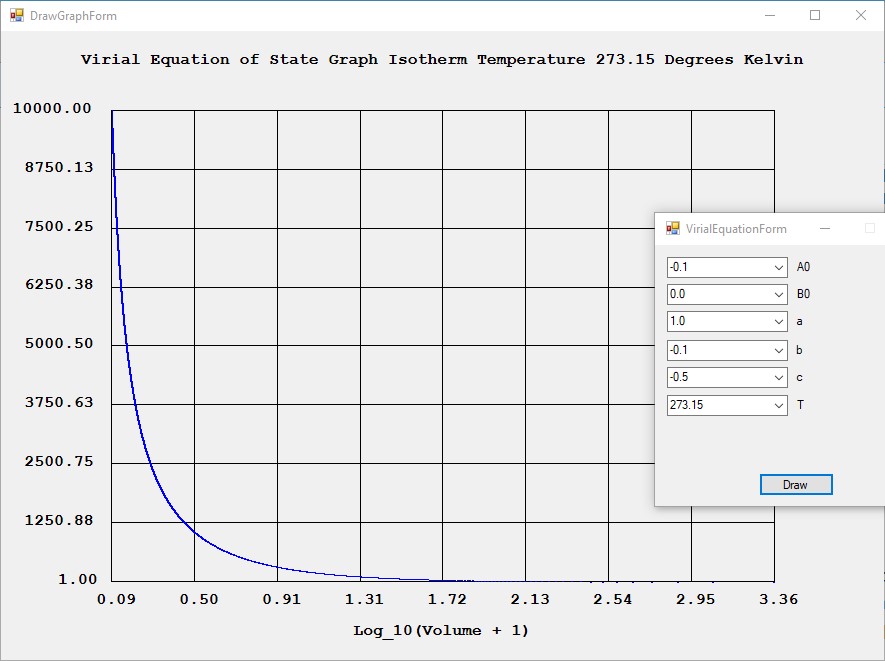
I created a C# application to model an ideal gas and real gases. The real gas algorithms were the Van der Waal Equation of State and the Virial Equation of State.
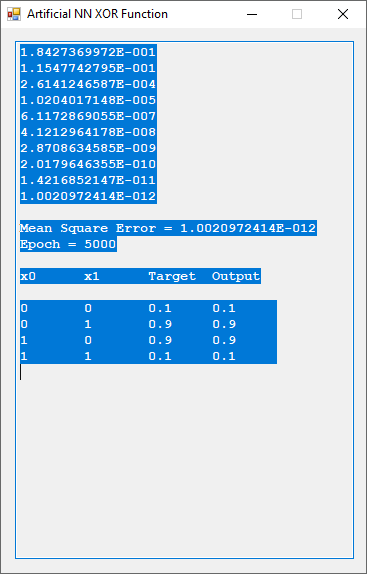
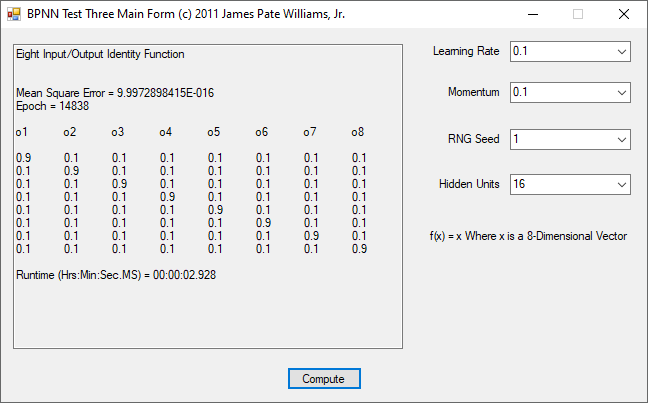
The functions to be calculated are the exclusive or (XOR) function, the eight input and output identity function, and four non-linear three input and one output functions. I used the logistic function that represents 0 as 0.1 and 1 as 0.9. The three input functions use 8 hidden units, a tolerance of 1.0e-9, and maximum number of epochs as 1,000,000. The backpropagation feed-forward neural network algorithm is from Tom M. Mitchell’s classic textbook “Machine Learning” which has a copyright of 1997.
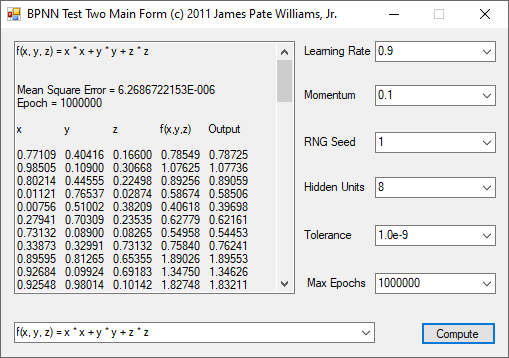
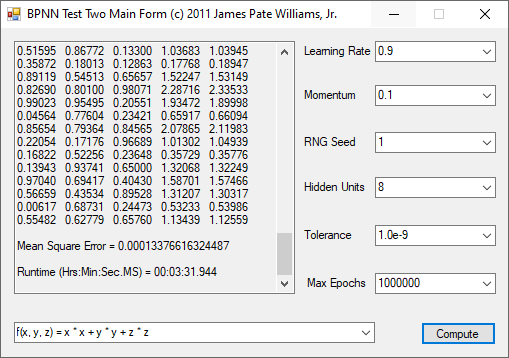
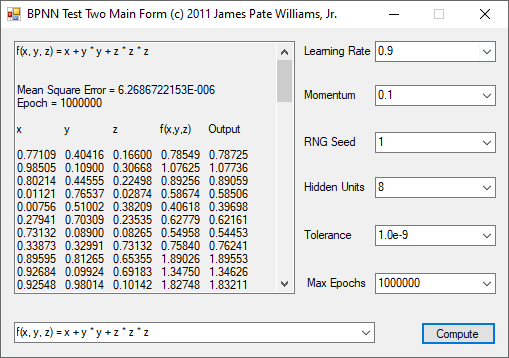
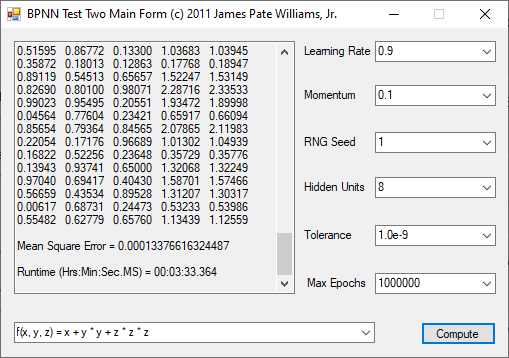
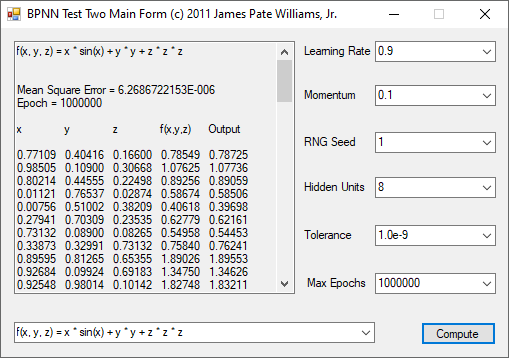
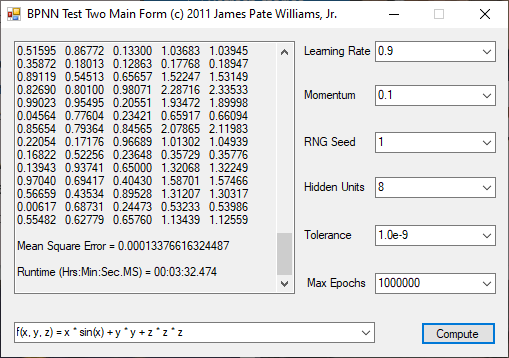
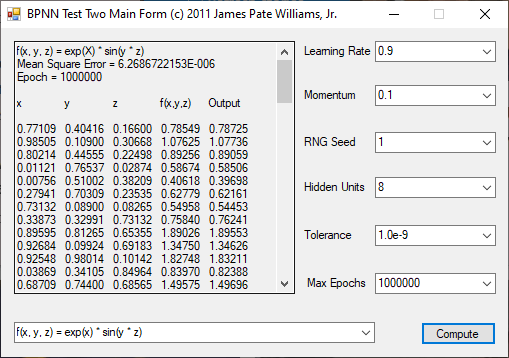
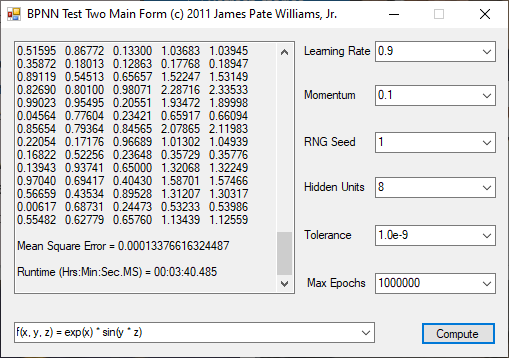
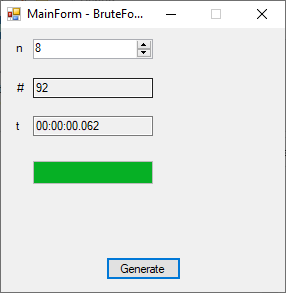
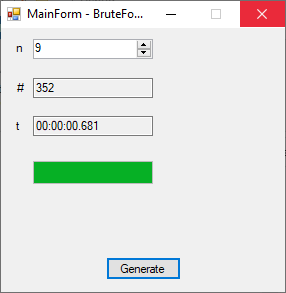
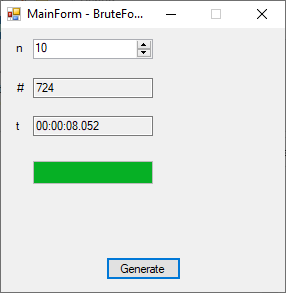
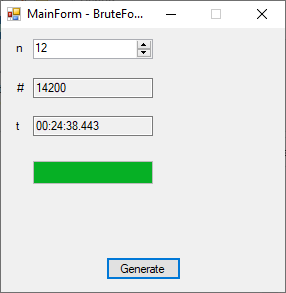
The n-queens problem is a constraint satisfaction problem. The object of the puzzle is to arrange n queens on a n x n chessboard, so that no two queens are attacking one another. Remember the chess queen can move any number of spaces diagonally, horizontally, or vertically. My brute force solver computes n factorial possible solutions and checks each configuration to see if it solves the n-queens puzzle. The n-queens problem is thought to be NP-Complete which means that solutions are found by a non-deterministic polynomial or exponential algorithm. My solutions seem to require 2^n seconds to find all solutions of the problem for n = 8 to 12. I generate n-factorial candidate solutions and test each candidate to see if it solves the n-queens problem.
| Brute Force Solutions of the N-Queens Problem | |||
| n | n! | # | Time (s) |
| 8 | 40,320 | 92 | 0 |
| 9 | 362,880 | 352 | 1 |
| 10 | 3,628,800 | 724 | 8 |
| 11 | 39,916,800 | 2,680 | 105 |
| 12 | 479,001,600 | 14,200 | 1478 |

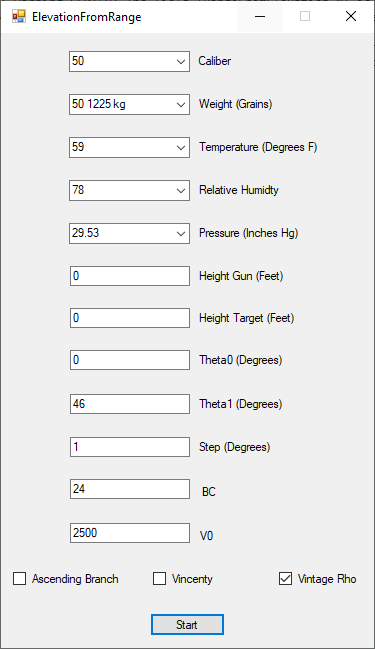
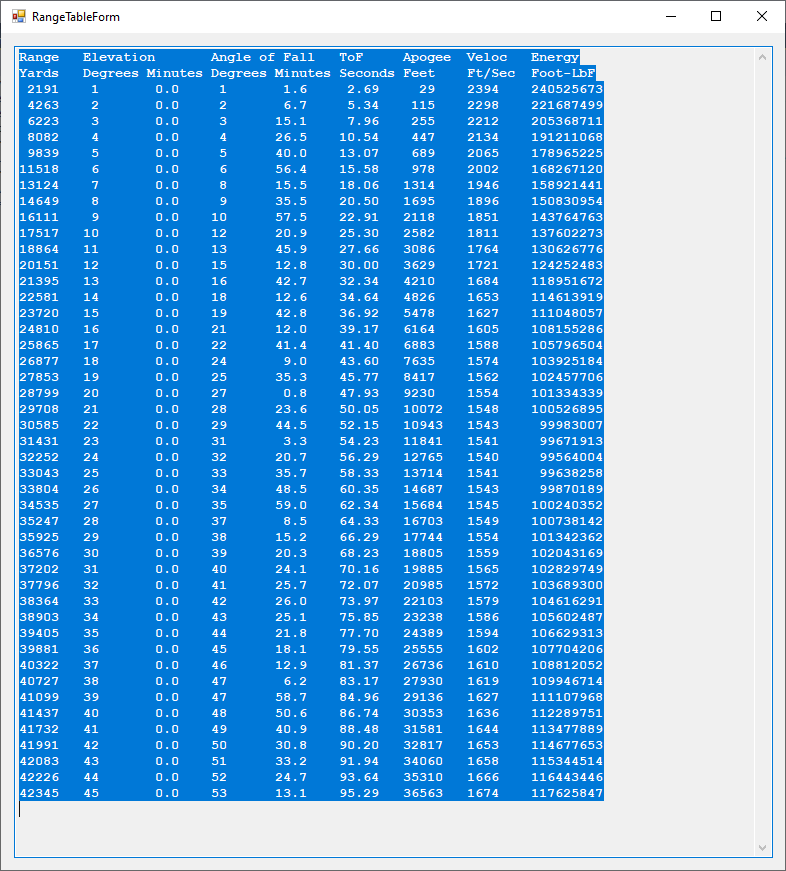
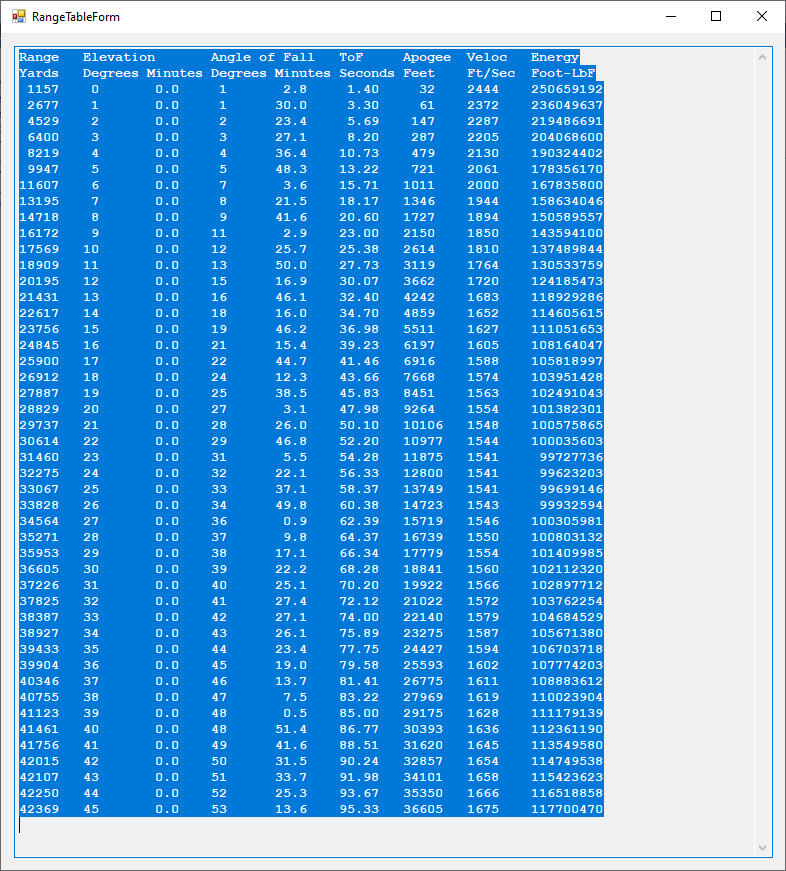
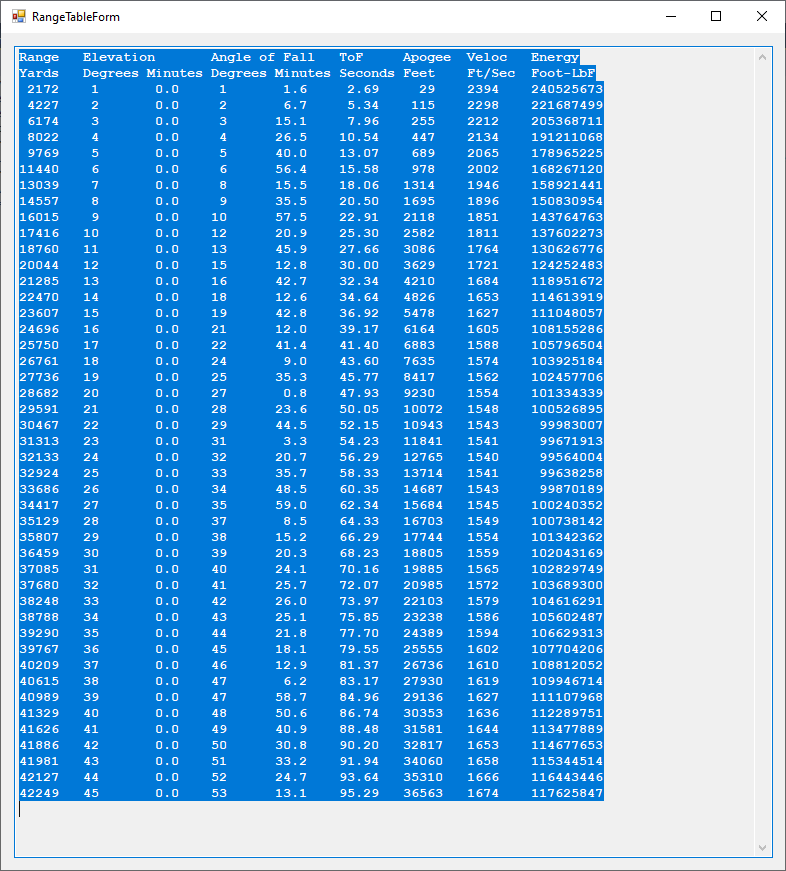
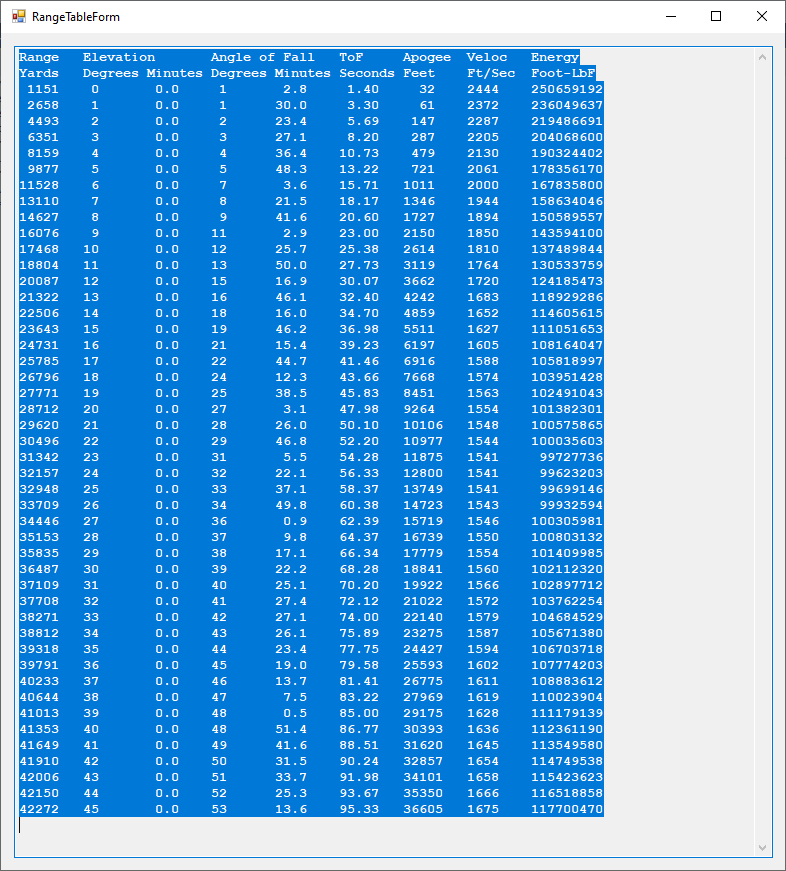
This is another attempt to reproduce the United States Navy’s Ordnance Pamphlet 770: https://eugeneleeslover.com/USN-GUNS-AND-RANGE-TABLES/OP-770-1.html which contains ballistic tables for the battleship USS Iowa (BB-61) artillery (16-inch/50 caliber) and is dated October 1941. My C# Windows desktop application is capable of calculating the elevation from range table which has the columns range in yards, angle of elevation in degrees and minutes, positive angle of fall in degrees and minutes, time of flight in seconds, apogee also called summit in feet, striking velocity in feet per second, and energy in foot pound force. Three corrections can be applied to the trajectory: trunnion height in feet, acceleration of gravity correction, and the curvature of the Earth correction (Vincenty calculation). The first image below is the ballistic settings interface. The second image is the uncorrected table. The third image is the application of a trunnion height of 32 feet. The fourth image is the curvature of the Earth correction. The fifth image is the trunnion height of 32 feet and Vincenty corrections. It is to be noticed that the striking velocity and kinetic energy are the only non-monotonically increasing or decreasing data fields.
I became interested in attempting to predict average annual temperatures in the state of Georgia way back in the day. I found a neat website for temperatures for January 1895 to December 2001. Unfortunately, the website no longer exists online, however, I saved the data to an extinct PC of mine and a USB solid state drive. I used several methods to attempt predictions of the annual temperatures from 2002 to 2025. The first algorithm is polynomial least squares utilizing a 32-degree polynomial and a 75-degree polynomial. The application was written in one of my favorite programming languages, namely, C#.


