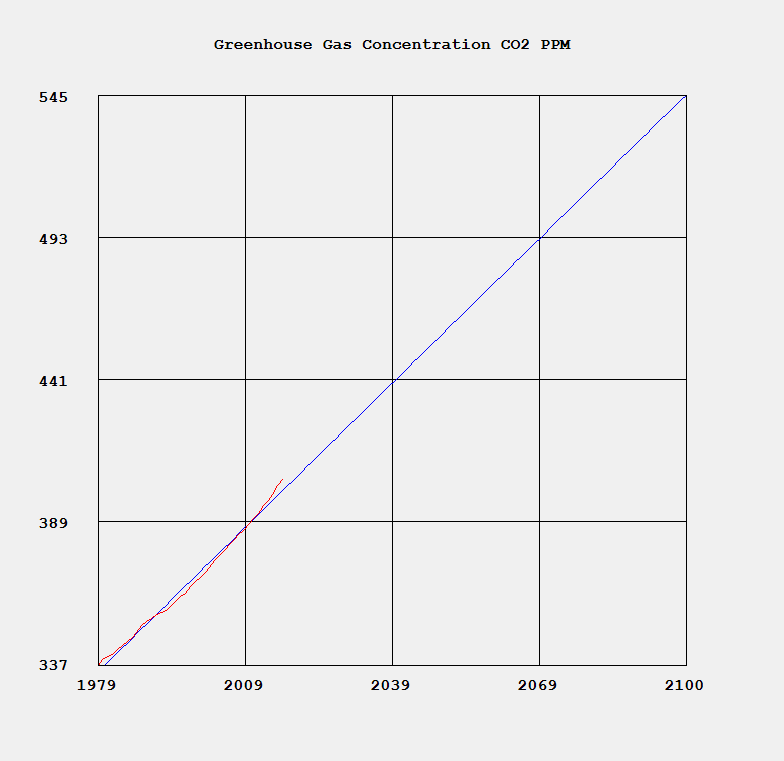
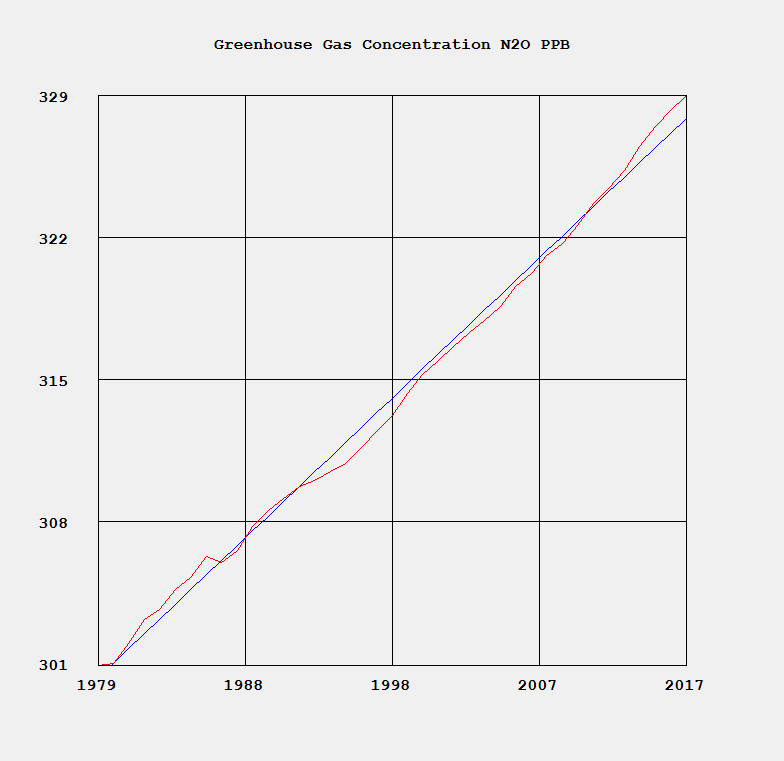
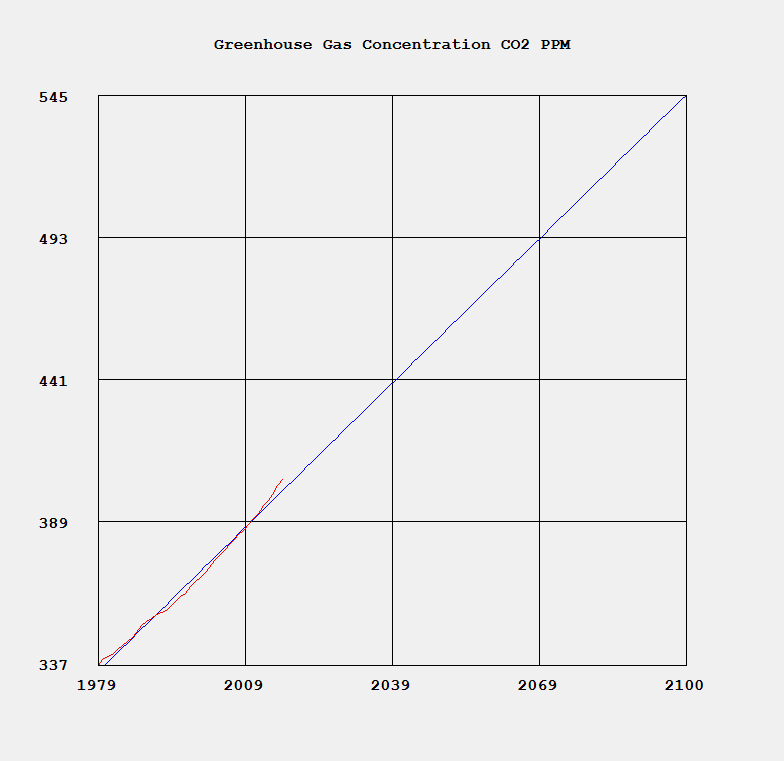
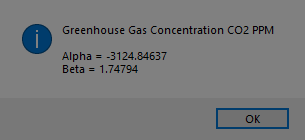
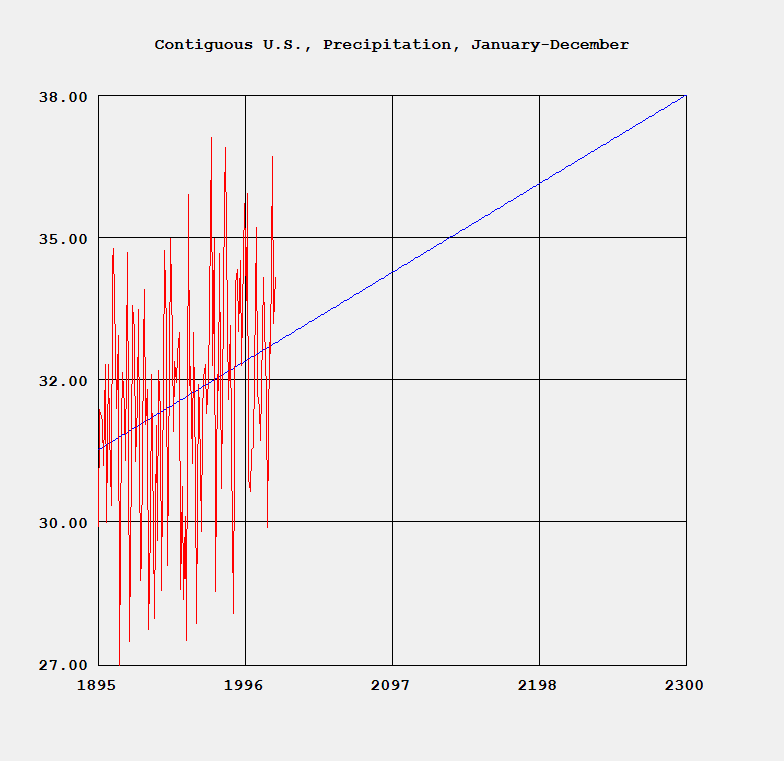
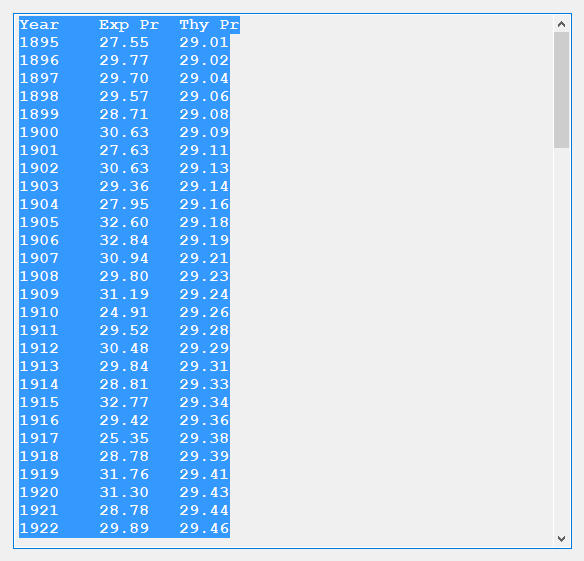
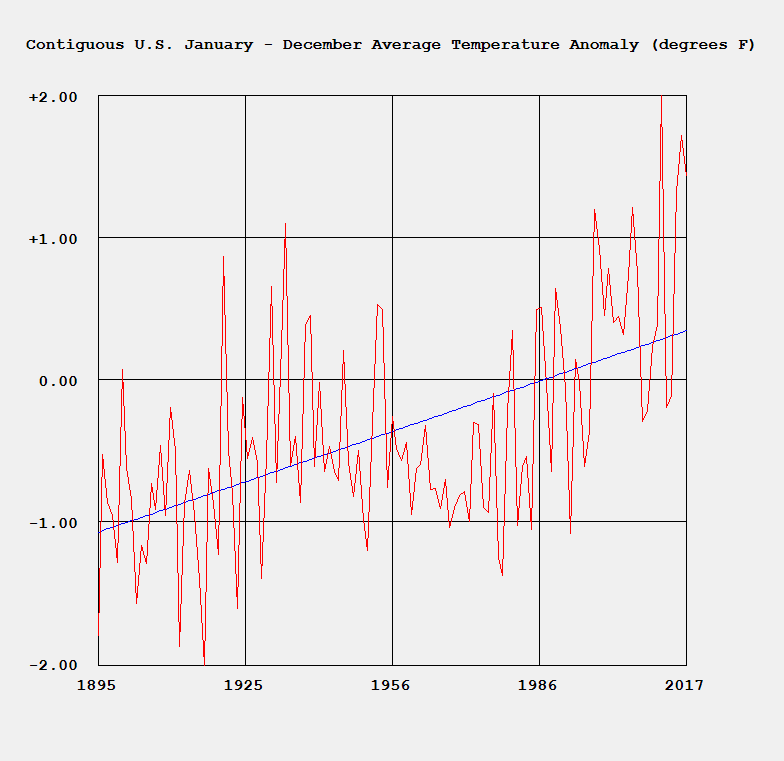
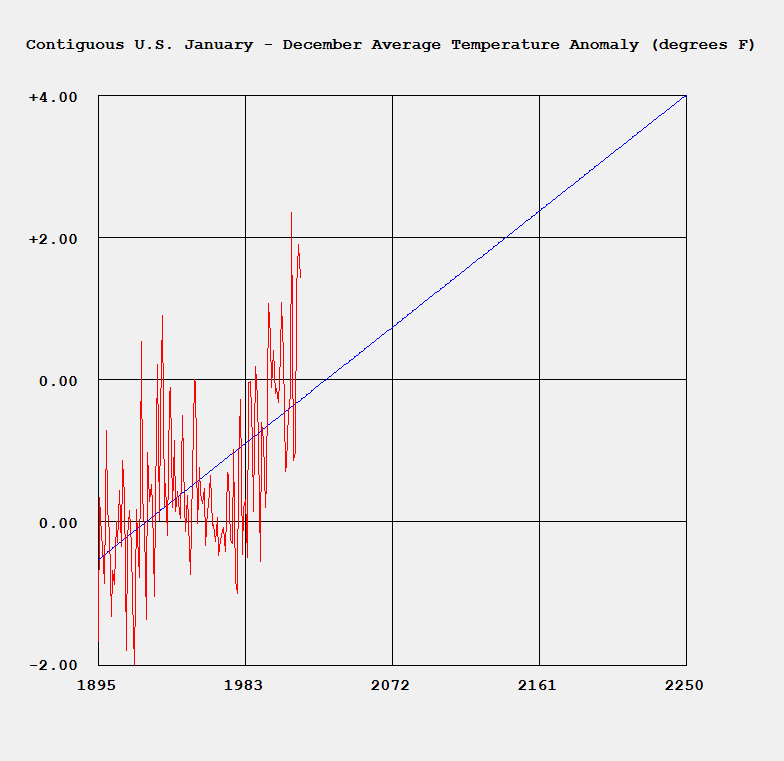
http://en.wikipedia.org/wiki/Ulam_numbers
Stanislaw Marcin Ulam worked on the Manhattan Project by an invitation from John von Neumann:
https://en.wikipedia.org/wiki/Stanis%C5%82aw_Ulam#Move_to_the_United_States
Ulam is given credit for the Teller-Ulam design of the hydrogen bomb. Edward Teller was one of the first proponent of human induced global climate change:
https://en.wikipedia.org/wiki/Edward_Teller#Hydrogen_bomb
/*
Translator: James Pate Williams, Jr. (c) 2008
Translated to C++ from the following python code:
http://en.wikipedia.org/wiki/Ulam_numbers
https://oeis.org/A002858
ulam_i = [1,2,3]
ulam_j = [1,2,3]
for cand in range(4,5000):
res = []
for i in ulam_i:
for j in ulam_j:
if i == j or j > i: pass
else:
res.append(i+j)
if res.count(cand) == 1:
ulam_i.append(cand)
ulam_j.append(cand)
print ulam_i
Find the Ulam primes <= 5000
*/
#include "stdafx.h"
#include <time.h>
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
bool sieve[10000000];
void PopulateSieve(bool *sieve, int number) {
// sieve of Eratosthenes
int c, inc, i, n = number - 1;
for (i = 0; i < n; i++)
sieve[i] = false;
sieve[1] = false;
sieve[2] = true;
for (i = 3; i <= n; i++)
sieve[i] = (i & 1) == 1 ? true : false;
c = 3;
do {
i = c * c;
inc = c + c;
while (i <= n) {
sieve[i] = false;
i += inc;
}
c += 2;
while (!sieve[c])
c++;
} while (c * c <= n);
}
bool CountEqualOne(int number, vector<int> ulam) {
int count = 0, i;
for (i = 0; i < ulam.size(); i++)
if (ulam[i] == number)
count++;
return count == 1;
}
void UlamNumbers(int n) {
int candidate, i, j;
vector<int> vI;
vector<int> vJ;
vector<int> UlamResult;
PopulateSieve(sieve, 10000000);
for (i = 1; i <= 3; i++) {
vI.push_back(i);
vJ.push_back(i);
}
for (candidate = 4; candidate <= n; candidate++) {
UlamResult.clear();
for (i = 0; i < vI.size(); i++) {
int ui = vI[i];
for (j = 0; j < vJ.size(); j++) {
int uj = vJ[j];
if (ui == uj || uj > ui)
continue;
UlamResult.push_back(ui + uj);
}
}
if (CountEqualOne(candidate, UlamResult)) {
vI.push_back(candidate);
vJ.push_back(candidate);
}
}
j = 0;
for (i = 0; i < vI.size(); i++) {
if (sieve[vI[i]]) {
cout << setw(4) << vI[i] << ' ';
if ((j + 1) % 10 == 0) {
j = 0;
cout << endl;
}
else
j++;
}
}
cout << endl;
}
int main(int argc, char * const argv[]) {
clock_t clock0 = clock();
cout << "Ulam sequence prime numbers < 5000" << endl << endl;
UlamNumbers(5000);
clock0 = clock() - clock0;
cout << endl << endl << "seconds = ";
cout << (double)clock0 / CLOCKS_PER_SEC << endl;
return 0;
}