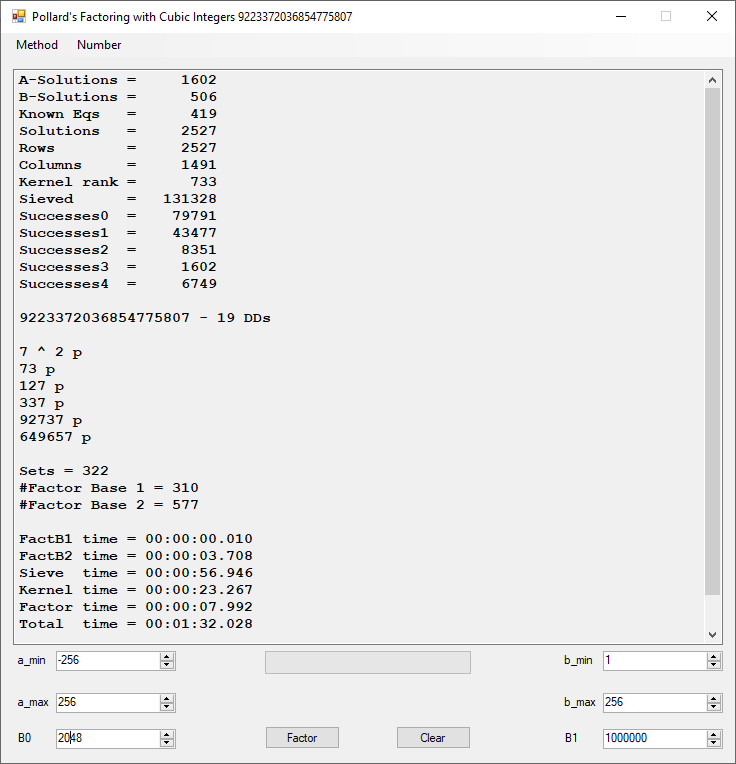
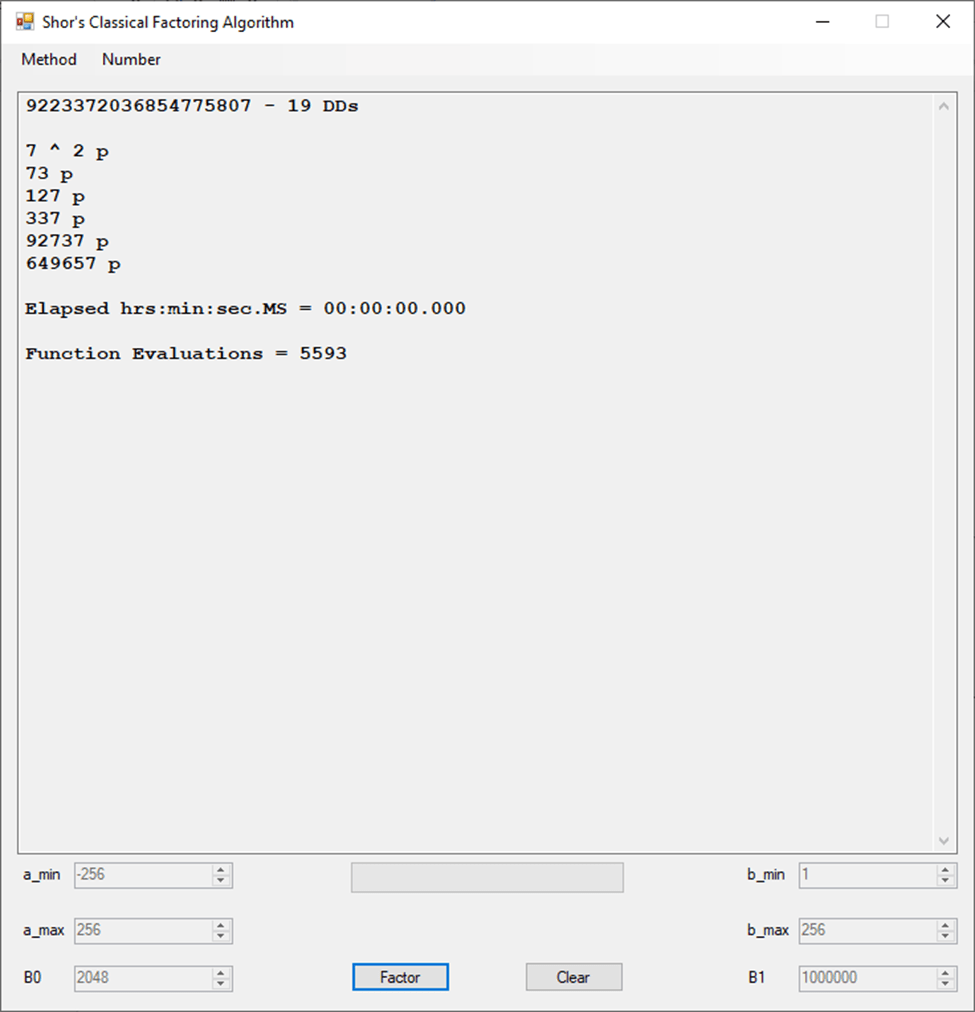
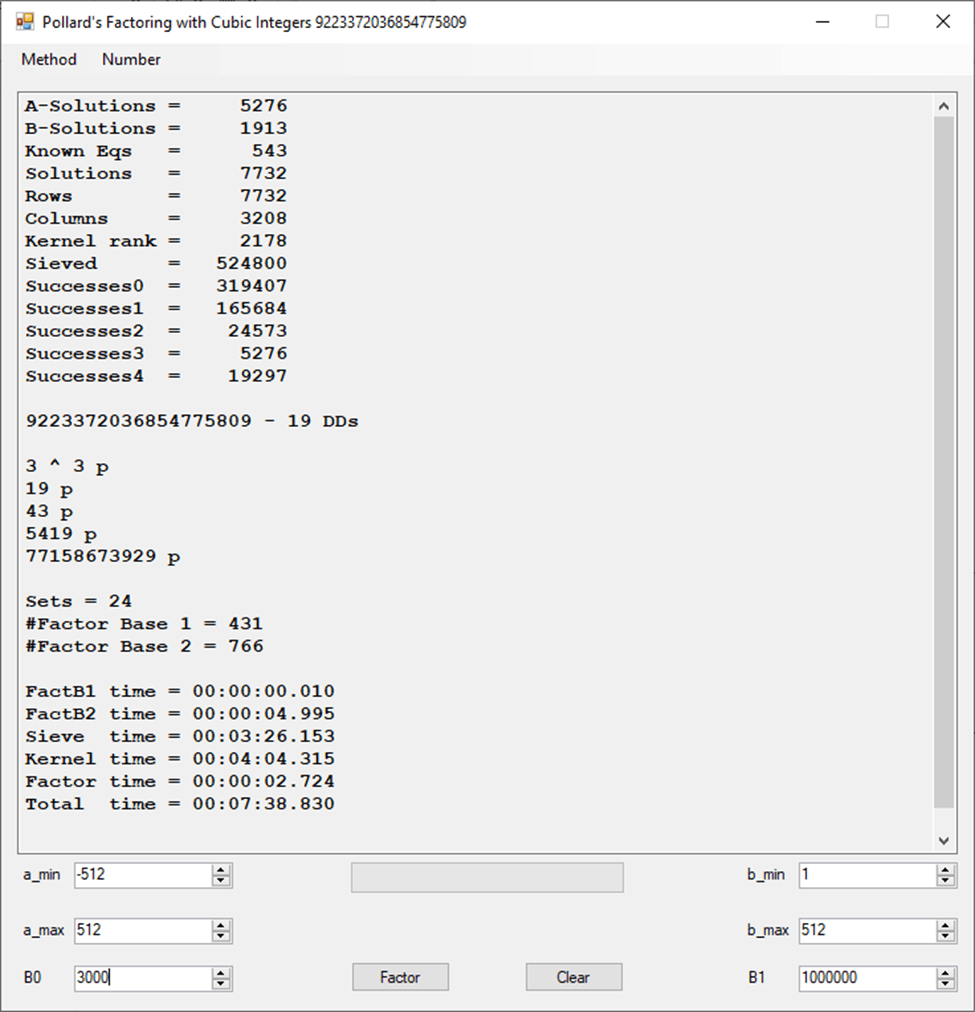
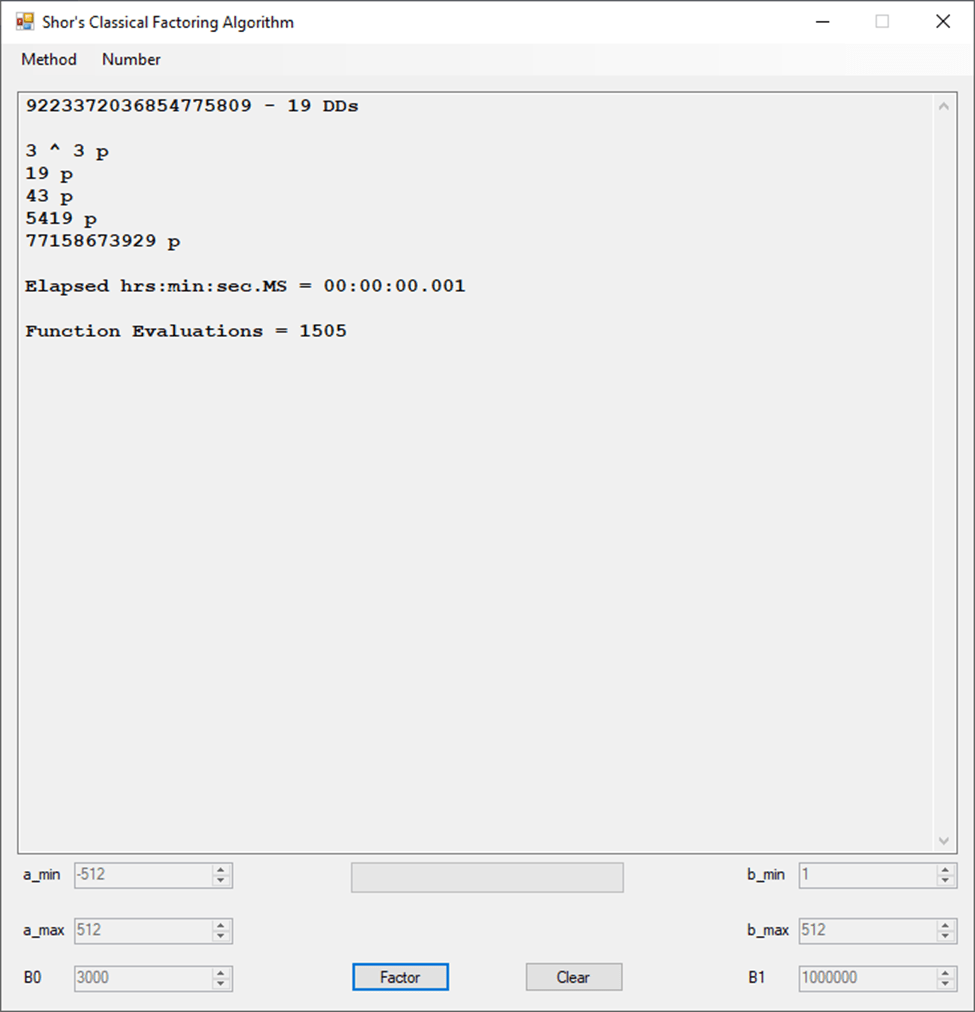
This set of experiments is dedicated to Alfred J. Menezes, Arjen K. Lenstra, H. W. Lenstra, Jr., J. M. Pollard, Henri Cohen, Hans Riesel, H. T. Lau, Charles Petzold, Richard O. Chapman, Gerry V. Dozier, Homer Carlisle, Fay A. Riddle, Brooks Shelhorse, among many others whose names have faded from my memory.
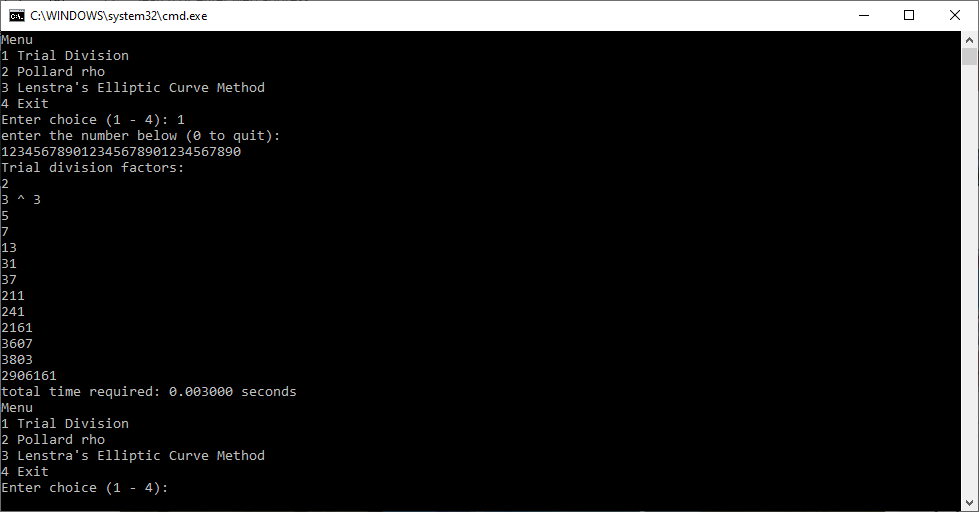
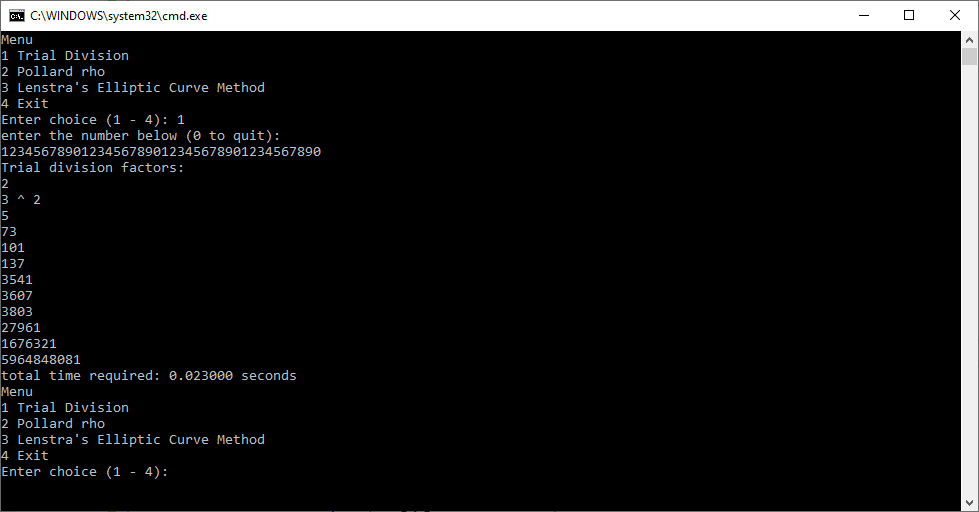
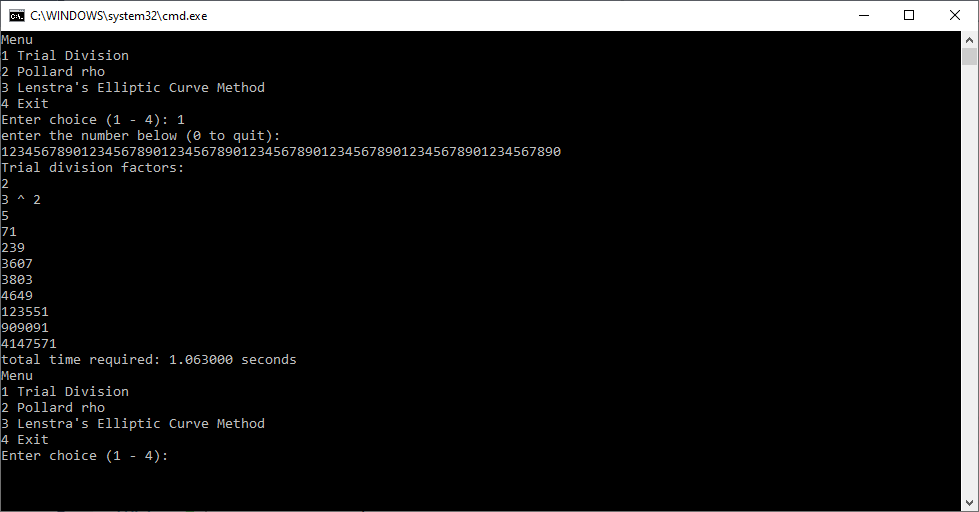
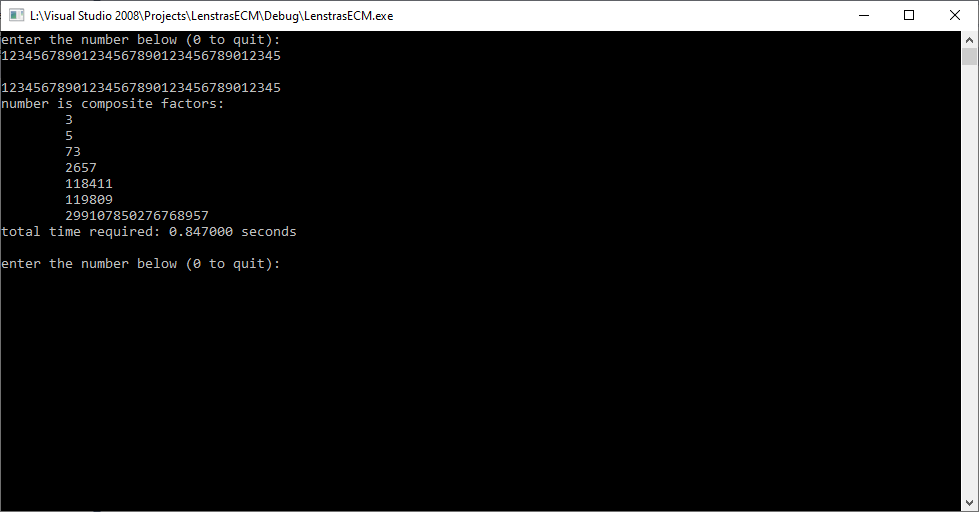
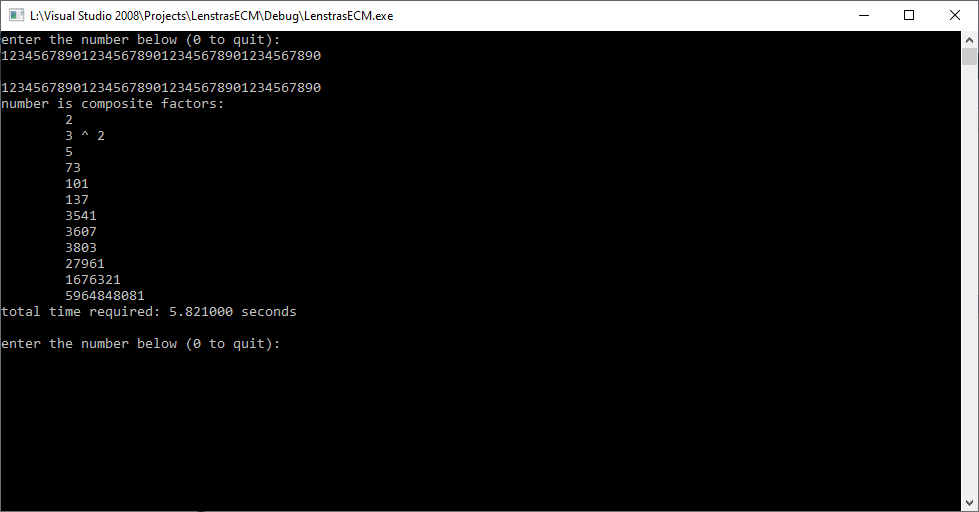
The factoring algorithms are trial division, Brent’s modification of the famous Pollard rho Method, and Lenstra’s Elliptic Curve Method. I used repetitions of the digit string “1234567890” of varying length. I chose these strings because of the richness of prime factors.
These algorithms are not guaranteed to completely factor these relatively large numbers. I gave up on using the elliptic curve method for numbers of greater than 40-digits. I have to give up on Brent’s modification of the Pollard rho method for numbers of more than 70-digits.
/*
Author: Pate Williams (c) 1997 - 2022
Algorithm 8.5.2 (Pollard rho). See "A Course in
Computational Algebraic Number Theory" by Henri
Cohen page 429.
Author: Pate Williams (c) 1997 - 2022
Algorithm 10.3.3 (Lenstra's ECM). See "A Course
in Computational Algebraic Number Theory" by
Henri Cohen page 488.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include "lip.h"
typedef struct fact {
verylong zf;
int expon;
} FACTOR, PFACTOR;
int BOUND = 100000000;
void add_factor(int e, verylong zp,
FACTOR f[], int *count)
{
int done = 0, found = 0, i, j = 0;
for (i = 0; !done && i < *count; i++)
{
found = zcompare(zp, f[i].zf);
if (found == 0)
{
done = 1;
j = i;
}
}
if (found == 0)
{
for (i = *count - 2; i >= j; i--)
{
f[i + 1].expon = f[i].expon;
zcopy(f[i].zf, &f[i + 1].zf);
}
*count = *count + 1;
f[j].expon = e;
zcopy(zp, &f[j].zf);
}
else if (found == 0)
f[j].expon++;
else
{
f[*count].expon = e;
zcopy(zp, &f[*count].zf);
*count = *count + 1;
}
}
int trial_division(verylong *zN, FACTOR f[], int *count)
{
int e, one = 0, pr = 0;
long B, p;
verylong za = 0, zb = 0, zp = 0;
zsqrt(*zN, &za, &zb);
if (zscompare(za, BOUND) > 0)
B = BOUND;
else
B = ztoint(za);
zcopy(*zN, &za);
zpstart2();
do {
p = zpnext();
if (zsmod(za, p) == 0)
{
e = 0;
do {
zsdiv(za, p, &zb);
zcopy(zb, &za);
e++;
} while (zsmod(za, p) == 0);
zintoz(p, &zp);
add_factor(e, zp, f, count);
zcopy(za, zN);
one = zscompare(*zN, 1l) == 0;
if (!one)
pr = zprobprime(*zN, 5l);
}
} while (!one && !pr && p <= B);
if (pr)
add_factor(1, *zN, f, count);
zfree(&za);
zfree(&zb);
zfree(&zp);
return p <= B;
}
void Brent(verylong *zN, FACTOR f[], int *count)
{
int e, one, pr;
long c, i, k, l;
verylong zP = 0, za = 0, zb = 0, zg = 0, zn = 0;
verylong zx = 0, zx1 = 0, zy = 0;
zcopy(*zN, &zn);
do {
c = 0, k = l = 1;
zone(&zP);
zintoz(2l, &zy);
zintoz(2l, &zx);
zintoz(2l, &zx1);
L2:
zsq(zx, &za);
zsadd(za, 1l, &zb);
zmod(zb, zn, &zx);
zsub(zx1, zx, &za);
zmulmod(za, zP, zn, &zb);
zcopy(zb, &zP);
if (++c == 20) {
zgcd(zP, zn, &zg);
if (zscompare(zg, 1l) > 0) goto L4;
zcopy(zx, &zy);
c = 0;
}
if (--k != 0)
goto L2;
zgcd(zP, zn, &zg);
if (zscompare(zg, 1l) > 0)
goto L4;
zcopy(zx, &zx1);
k = l, l *= 2;
for (i = 0; i < k; i++)
{
zsq(zx, &za);
zsadd(za, 1l, &zb);
zmod(zb, zn, &zx);
}
zcopy(zx, &zy);
c = 0;
goto L2;
L4:
do {
zsq(zy, &za);
zsadd(za, 1l, &zb);
zmod(zb, zn, &zy);
zsub(zx1, zy, &za);
zgcd(za, zn, &zg);
} while (zscompare(zg, 1l) == 0);
if (zcompare(zg, zn) == 0) {
fprintf(stderr, "fatal error\nBrent's method failed\n");
exit(1);
}
if (!zprobprime(zg, 20l))
{
zcopy(zg, &za);
if (!trial_division(&zg, f, count)) {
fprintf(stderr, "fatal error\ncould not trial divide\n");
exit(1);
}
zcopy(za, &zg);
zdiv(zn, zg, &za, &zb);
zcopy(za, &zn);
}
else
{
e = 0;
do {
zdiv(zn, zg, &za, &zb);
zcopy(za, &zn);
zmod(zn, zg, &za);
e++;
} while (zscompare(za, 0l) == 0);
add_factor(e, zg, f, count);
}
one = zscompare(zn, 1l) == 0;
if (!one) pr = zprobprime(zn, 5l);
} while (!one && !pr);
if (!one)
add_factor(1, zn, f, count);
zfree(&zP);
zfree(&za);
zfree(&zb);
zfree(&zg);
zfree(&zn);
zfree(&zx);
zfree(&zx1);
zfree(&zy);
}
int partition(FACTOR a[], int n, int lo, int hi)
{
int pivotIndex = lo + (hi - lo) / 2;
FACTOR x = a[pivotIndex];
FACTOR t = x;
a[pivotIndex] = a[hi];
a[hi] = t;
int storeIndex = lo;
for (int i = lo; i < hi; i++)
{
if (zcompare(a[i].zf, x.zf) < 0)
{
t = a[i];
a[i] = a[storeIndex];
a[storeIndex++] = t;
}
}
t = a[storeIndex];
a[storeIndex] = a[hi];
a[hi] = t;
return storeIndex;
}
void do_quick_sort(FACTOR a[], int n, int p, int r)
{
if (p < r)
{
int q = partition(a, n, p, r);
do_quick_sort(a, n, p, q - 1);
do_quick_sort(a, n, q + 1, r);
}
}
void quick_sort(FACTOR a[], int n)
{
do_quick_sort(a, n, 0, n - 1);
}
#ifndef CLK_TCK
#define CLK_TCK CLOCKS_PER_SEC
#endif
#define CURVES 1024l
struct point { verylong zx, zy, zz; };
struct factor { int expon; verylong prime; };
static char cexp[32][32], cfac[32][512];
static int cnt, primeCount;
int partial_addition(verylong za,
verylong zn,
struct point P,
struct point Q,
struct point *R,
verylong *zd)
/* returns 0 if sum is found or 1 if divisor is found */
{
int value = 0;
verylong zb = 0, zc = 0, zl = 0, zs = 0, zt = 0;
verylong zx = 0, zy = 0, zy2 = 0;
if (zcompare(P.zx, Q.zx) == 0 &&
zscompare(P.zy, 0l) == 0 &&
zscompare(Q.zy, 0l) == 0) {
zzero(&R->zx);
zone(&R->zy);
return 0;
}
zsub(zn, Q.zy, &zb);
if (zcompare(P.zx, Q.zx) == 0 &&
zcompare(P.zy, zb) == 0) {
zzero(&R->zx);
zone(&R->zy);
zfree(&zb);
return 0;
}
if (zscompare(P.zx, 0l) == 0 &&
zscompare(P.zy, 1l) == 0 &&
zscompare(P.zz, 0l) == 0) {
/* O + Q = Q */
zcopy(Q.zx, &R->zx);
zcopy(Q.zy, &R->zy);
zcopy(Q.zz, &R->zz);
value = 0;
}
else if (zscompare(Q.zx, 0l) == 0 &&
zscompare(Q.zy, 1l) == 0 &&
zscompare(Q.zz, 0l) == 0) {
/* P + O = P */
zcopy(P.zx, &R->zx);
zcopy(P.zy, &R->zy);
zcopy(P.zz, &R->zz);
value = 0;
}
else {
/* P != O and Q != O */
zcopy(Q.zy, &zy2);
znegate(&zy2);
if (zcompare(P.zx, Q.zx) == 0 &&
zcompare(P.zy, zy2) == 0) {
zzero(&R->zx);
zone(&R->zy);
zzero(&R->zz);
}
else {
if (zcompare(P.zx, Q.zx) != 0) {
zsubmod(P.zx, Q.zx, zn, &zx);
zexteucl(zx, &zs, zn, &zt, zd);
if (zscompare(*zd, 1l) != 0) goto L1;
zsubmod(P.zy, Q.zy, zn, &zy);
zmulmod(zs, zy, zn, &zl);
}
else {
zaddmod(P.zy, Q.zy, zn, &zy);
zexteucl(zy, &zs, zn, &zt, zd);
if (zscompare(*zd, 1l) != 0) goto L1;
zmulmod(P.zx, P.zx, zn, &zb);
zsmulmod(zb, 3l, zn, &zc);
zaddmod(zc, za, zn, &zb);
zmulmod(zs, zb, zn, &zl);
}
zmulmod(zl, zl, zn, &zb);
zaddmod(P.zx, Q.zx, zn, &zc);
zsubmod(zb, zc, zn, &zx);
zcopy(zx, &R->zx);
zsubmod(zx, P.zx, zn, &zb);
zmulmod(zl, zb, zn, &zc);
zaddmod(zc, P.zy, zn, &zy);
znegate(&zy);
zcopy(zy, &R->zy);
zone(&R->zz);
goto L2;
L1:
value = 1;
L2:
;
}
}
zfree(&zb);
zfree(&zc);
zfree(&zl);
zfree(&zs);
zfree(&zt);
zfree(&zx);
zfree(&zy);
zfree(&zy2);
return value;
}
int multiply(long k,
verylong za,
verylong zn,
struct point P,
struct point *R,
verylong *zd)
{
int value = 0;
struct point A, S, T;
A.zx = A.zy = A.zz = S.
zx = S.zy = S.zz = 0;
T.zx = T.zy = T.zz = 0;
zzero(&R->zx);
zone(&R->zy);
zzero(&R->zz);
zcopy(P.zx, &S.zx);
zcopy(P.zy, &S.zy);
zcopy(P.zz, &S.zz);
while (!value && k != 0) {
if (k & 1) {
value = partial_addition(za, zn, *R, S, &A, zd);
zcopy(A.zx, &R->zx);
zcopy(A.zy, &R->zy);
zcopy(A.zz, &R->zz);
}
k >>= 1;
if (!value && k != 0) {
value = partial_addition(za, zn, S, S, &T, zd);
zcopy(T.zx, &S.zx);
zcopy(T.zy, &S.zy);
zcopy(T.zz, &S.zz);
}
}
if (zscompare(R->zy, 0l) < 0) {
zadd(R->zy, zn, &A.zy);
zcopy(A.zy, &R->zy);
}
zfree(&A.zx);
zfree(&A.zy);
zfree(&A.zz);
zfree(&S.zx);
zfree(&S.zy);
zfree(&S.zz);
zfree(&T.zx);
zfree(&T.zy);
zfree(&T.zz);
return value;
}
/* the following definition limits the L3 loop */
int LenstrasECM(verylong *zN, verylong *zg)
{
int expon = 0, found = 0;
long B = 2000000l, i, j, k = 0, l, *p, q, q1;
long giveUp = z2log(*zN);
struct point x, y;
verylong za[CURVES], zb = 0, zd = 0;
for (i = 0; i < CURVES; i++)
za[i] = 0;
x.zx = x.zy = x.zz = y.zx = y.zy = y.zz = 0;
zpstart2();
do {
q = zpnext();
k++;
} while (q < B);
p = calloc(k, sizeof(long));
if (!p) {
expon = -1;
goto L4;
}
zpstart2();
for (i = 0; i < k; i++)
p[i] = zpnext();
for (i = 0; i < CURVES; i++)
zrandomb(*zN, &za[i]);
L2:
zone(&x.zx);
zone(&x.zy);
zzero(&x.zz);
i = -1;
L3:
i++;
if (i == giveUp) {
expon = 0;
goto L4;
}
if (i == k) {
for (i = 0; i < CURVES; i++)
zrandomb(*zN, &za[i]);
goto L2;
}
q = p[i];
q1 = q;
l = B / q;
while (q1 <= l)
q1 *= q;
found = 0;
for (j = 0; !found && j < CURVES; j++)
found = multiply(q1, za[j], *zN, x, &y, &zd);
if (!found)
goto L3;
zcopy(y.zx, &x.zx);
zcopy(y.zy, &x.zy);
zcopy(y.zz, &x.zz);
zgcd(zd, *zN, zg);
if (zcompare(*zg, *zN) == 0) {
for (j = 0; j < CURVES; j++)
zrandomb(*zN, &za[j]);
goto L2;
}
if (!zprobprime(*zg, 5l))
goto L4;
expon = 0;
do {
zdiv(*zN, *zg, &zb, &zd);
zcopy(zb, zN);
zmod(*zN, *zg, &zd);
expon++;
} while (zscompare(zd, 0l) == 0);
L4:
for (i = 0; i < CURVES; i++)
zfree(&za[i]);
zfree(&zb);
zfree(&zd);
zfree(&x.zx);
zfree(&x.zy);
zfree(&x.zz);
zfree(&y.zx);
zfree(&y.zy);
zfree(&y.zz);
return expon;
}
int ECMVLConvert(verylong zx, char *str, int length)
{
verylong zy = 0;
int a, result = 1, i = 0;
while (zscompare(zx, 0) > 0)
{
zsdiv(zx, 10, &zy);
a = zsmod(zx, 10);
zcopy(zy, &zx);
if (i < length)
str[i++] = a + '0';
else
{
result = 0;
break;
}
}
str[i] = '\0';
_strrev(str);
zfree(&zy);
return result;
}
int ECMLast(char exp[32][32], char fac[32][512], struct factor *f, int *cnt)
{
int i;
for (i = 0; i < *cnt; i++)
{
if (ECMVLConvert(f[i].prime, fac[i], 512) == 1)
sprintf(exp[i], "%d", f[i].expon);
else
return 0;
}
return 1;
}
int DoECM(char exp[32][32], char fac[32][512], char *numStr,
int *cnt, int base, int iExpon, int addend)
{
struct factor f[32];
int i, j, result;
int cant, expon, one, pri;
verylong zn = 0, zN = 0, zd = 0, zg = 0;
if (strlen(numStr) != 0)
zstrtoz(numStr, &zN);
else
{
static verylong zb = 0, zp = 0;
zintoz(base, &zb);
zsexp(zb, iExpon, &zp);
zsadd(zp, addend, &zN);
}
zcopy(zN, &zn);
for (i = 0; i < 32; i++)
{
f[i].expon = 0;
f[i].prime = 0;
}
*cnt = 0;
f[*cnt].expon = 1;
zcopy(zN, &f[*cnt].prime);
*cnt = *cnt + 1;
if (z2log(zn) > 512)
{
result = 3;
goto L1;
}
if (zprobprime(zN, 5l))
{
result = 2;
goto L1;
}
cant = pri = 0;
do {
expon = LenstrasECM(&zN, &zg);
if (expon == -1)
{
result = -1;
goto L1;
}
if (zprobprime(zg, 5l))
{
f[*cnt].expon = expon;
zcopy(zg, &f[*cnt].prime);
*cnt = *cnt + 1;
}
one = zscompare(zN, 1l) == 0;
if (zprobprime(zN, 5l))
{
f[*cnt].expon = 1;
zcopy(zN, &f[*cnt].prime);
*cnt = *cnt + 1;
break;
}
} while (!one);
/* selection sort the factors */
for (i = 1; i < *cnt - 1; i++)
{
for (j = i + 1; j < *cnt; j++)
{
if (zcompare(f[i].prime, f[j].prime) > 0)
{
int temp;
verylong zt = 0;
zcopy(f[i].prime, &zt);
zcopy(f[j].prime, &f[i].prime);
zcopy(zt, &f[j].prime);
temp = f[i].expon;
f[i].expon = f[j].expon;
f[j].expon = temp;
}
}
}
result = ECMLast(exp, fac, f, cnt);
L1:
if (result == 2)
{
int temp = ECMLast(exp, fac, f, cnt);
if (temp == 0)
result = 3;
}
zfree(&zn);
zfree(&zN);
zfree(&zd);
zfree(&zg);
return result;
}
int PrimeCheck(char fac[32][512], int cnt)
{
int i, result = 0;
verylong zp = 0;
for (i = 0; i < cnt; i++)
{
zstrtoz(fac[i], &zp);
if (zprobprime(zp, 20l))
result++;
}
return result;
}
int ECMMethod(char *numStr, int base, int expon, int addend)
{
int i, result;
cnt = 0;
for (i = 0; i < 32; i++)
{
cexp[i][0] = '\0';
cfac[i][0] = '\0';
}
result = DoECM(cexp, cfac, numStr, &cnt, base, expon, addend);
primeCount = PrimeCheck(cfac, cnt);
return result;
}
int main()
{
int i = 0, zacount = 0;
verylong zN = 0, zf = 0, zn = 0, zo = 0;
verylong zq = 0, zr = 0, zs = 0;
FACTOR za[32] = { 0 };
zintoz(1, &zo);
while (1) {
clock_t time0;
char numStr[256] = { 0 }, option[256] = { 0 }, *bPtr, *ePtr;
double time;
int c, base, expon, addend, iExpon = 0, positive, result;
printf("Menu\n");
printf("1 Trial Division\n");
printf("2 Pollard rho\n");
printf("3 Lenstra's Elliptic Curve Method\n");
printf("4 Exit\n");
printf("Enter choice (1 - 4): ");
c = getchar();
i = 0;
while (c != '\n' && i < 256)
{
option[i++] = c;
c = getchar();
}
option[i] = '\0';
if (option[0] == '4')
break;
if (option[0] < '1' || option[0] > '3')
{
printf("Unknown choice, please reenter choice\n");
continue;
}
printf("enter the number below (0 to quit):\n");
i = 0;
c = getchar();
while (c != '\n' && i < 256)
{
numStr[i++] = c;
c = getchar();
}
numStr[i] = '\0';
bPtr = strchr(numStr, '^');
if (bPtr != NULL)
{
*bPtr = '\0';
base = atoi(numStr);
ePtr = strchr(bPtr + 1, '+');
if (ePtr != NULL)
positive = 1;
else
{
ePtr = strchr(bPtr + 1, '-');
if (ePtr != NULL)
positive = 0;
}
if (ePtr != NULL)
*ePtr = '\0';
expon = atoi(bPtr + 1);
if (ePtr != NULL) {
addend = atoi(ePtr + 1);
if (positive == 0)
addend = -addend;
}
else
addend = 0;
numStr[0] = '\0';
}
else
{
addend = atoi(numStr);
if (addend == 0)
break;
}
if (strlen(numStr) != 0)
zstrtoz(numStr, &zN);
else
{
static verylong zb = 0, zp = 0;
zintoz(base, &zb);
zsexp(zb, iExpon, &zp);
zsadd(zp, addend, &zN);
}
zcopy(zN, &zn);
if (zmcomposite(zn, 20) == 0)
{
printf("Number is prime\n");
continue;
}
zacount = 0;
for (i = 0; i < 32; i++)
{
if (za[i].zf != 0)
zfree(&za[i].zf);
za[i].expon = 0;
}
time0 = clock();
if (option[0] == '1')
{
printf("Trial division factors:\n");
trial_division(&zN, za, &zacount);
}
else if (option[0] == '2')
{
printf("Pollard rho factors:\n");
Brent(&zN, za, &zacount);
}
else if (option[0] == '3')
{
printf("Lenstra's ECM factors:\n");
result = ECMMethod(numStr, base, expon, addend);
if (result == 0)
printf("can't completely factor this number\n");
else if (result == 1)
{
printf("%s\nnumber is composite factors:\n", cfac[0]);
for (i = 1; i < cnt; i++)
if (strcmp(cexp[i], "1") == 0)
printf("\t%s\n", cfac[i]);
else
printf("\t%s ^ %s\n", cfac[i], cexp[i]);
}
else if (result == 2)
printf("%s\nnumber is prime:\n", cfac[0]);
else if (result == 3)
printf("number or prime factor is too large\n");
}
if (option[0] < '3' && zacount > 0)
{
quick_sort(za, zacount);
for (i = 0; i < zacount; i++)
{
zwrite(za[i].zf);
if (za[i].expon > 1)
printf(" ^ %d ", za[i].expon);
printf("\n");
}
for (i = 0; i < zacount; i++)
if (za[i].zf != 0)
zfree(&za[i].zf);
zacount = 0;
}
time = (clock() - time0) / (double)CLK_TCK;
printf("total time required: %f seconds\n", time);
}
zfree(&zN);
zfree(&zn);
zfree(&zf);
zfree(&zo);
zfree(&zq);
zfree(&zr);
}