Category: Constraint Satisfaction Problems
Microsoft C# Constraint Satisfaction Dynamic Link Library (DLL) and Test Application

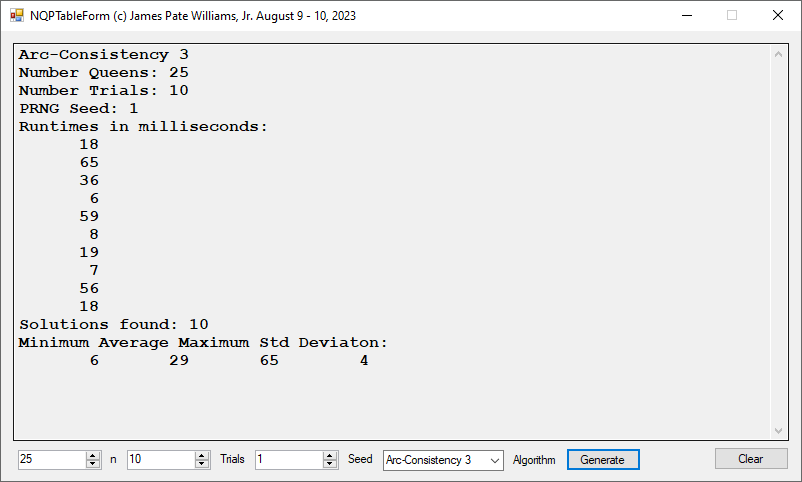




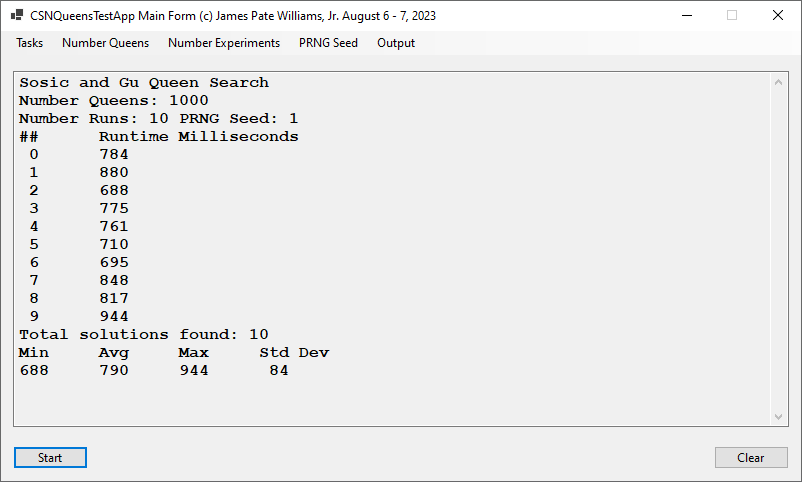
Constraint Satisfaction DLL Source Code Files Source Code File Lines of Code Arc.cs 42 Common.cs 214 Label.cs 62 NQPArcConsisitencies.cs 148 NQPBacktrack.cs 51 NQPSosicGu.cs 234 Vertex.cs 18 YakooGCPWCSA.cs 160 Total 929 Source Code File Lines of Code GCPGraphForm.cs 173 MainForm.cs 42 NQPGraphForm.cs 137 NQPTableForm.cs 223 Total 575 Source 1. Foundations of Constraint Satisfaction by Edward Tsang
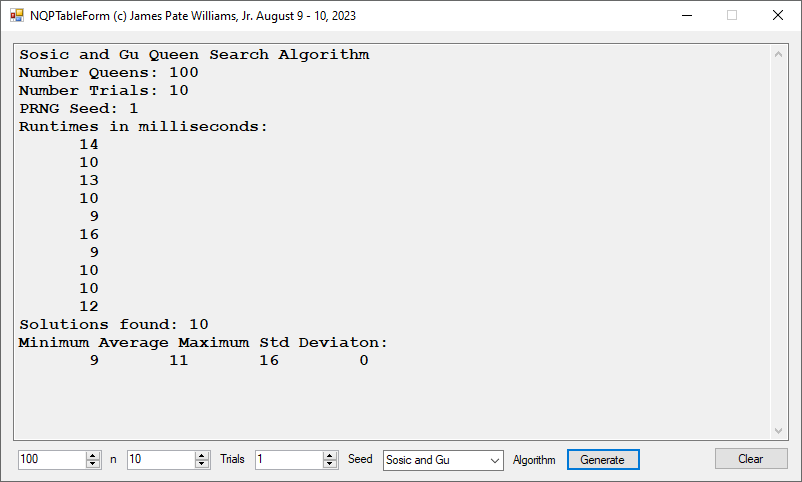
Sosic and Gu Fast N-Queens Problem Solver Implemented by James Pate Williams, Jr.
I implemented the Sosic and Gu fast N-Queens solver first in C++ and later in C#. The five screen shots below were created by latest C# application. None of my other algorithms can compete with this method.

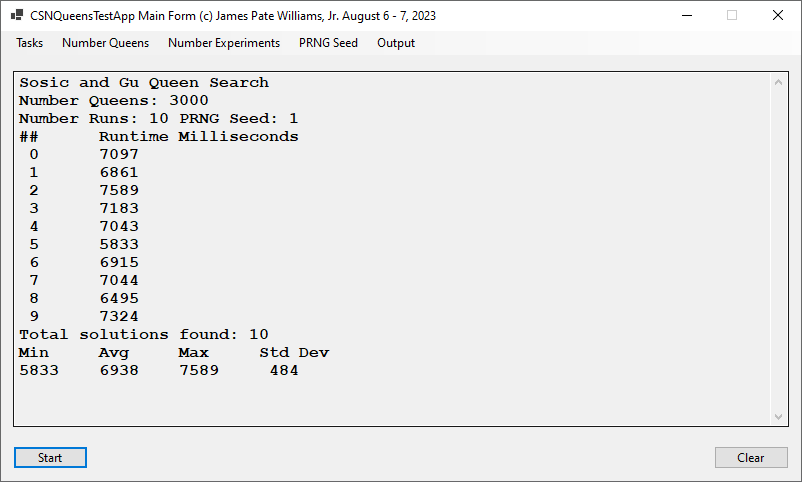


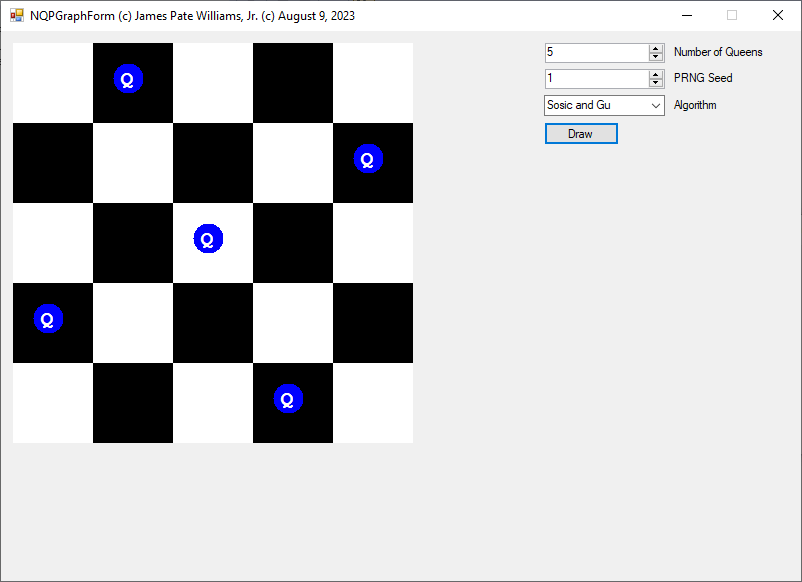
More N-Queens Puzzle Results by James Pate Williams, Jr.
N-Queens Tests 8 Queens Microseconds 50 Samples Algorithm Minimum Average Maximum Std Dev Arc-Consistency 3 1846 4148 14220 2294 Arc-Consistency 4 3850 8987 27903 5022 Backjump 175 1057 3873 883 Backmark 198 737 3323 596 Backtracking 171 789 3132 652 Hill-Climber 1991 2097 2913 157 9 Queens Microseconds 50 Samples Algorithm Minimum Average Maximum Std Dev Arc-Consistency 3 2628 5785 15748 3202 Arc-Consistency 4 7492 18057 56587 11114 Backjump 208 1410 6184 1325 Backmark 214 866 4468 880 Backtracking 210 1269 6156 1186 Hill-Climber 1309 1398 1953 102 10 Queens Microseconds 50 Samples Algorithm Minimum Average Maximum Std Dev Arc-Consistency 3 3820 10680 30708 6963 Arc-Consistency 4 12624 46645 148221 31212 Backjump 248 3970 16736 3805 Backmark 283 1504 7613 1433 Backtracking 227 2857 12882 3022 Hill-Climber 24575 25608 33563 2037
My hill-climber results are pretty disappointing. I have gotten some decent runs of back-marking for n = 50 and n = 60 queens. I show the n = 60 queens experiment below.
==Menu==
**Instance Submenu**
1 Single Instance Test
2 Multiple Instances Test
3 Exit
Enter an option '1' to '3': 2
**Algorithm Submenu**
1 Arc-Consistency 3
2 Arc-Consistency 4
3 Backjump
4 Backmark
5 Chronological Bactracking
6 Evolutionary Hill-Climber
7 Exit
Enter an algorithm ('1' to '7'): 4
Enter the number of queens for option '2': 60
Enter the number of samples to be analyzed: 10
Minimum Runtime in Microseconds: 4819
Average Runtime in Microseconds: 10419330
Maximum Runtime in Micorseconds: 45439444
Standard Sample Deviation: 16665688
Notice the misspelling of microseconds.
Six C++ Algorithms to Solve the N-Queens Puzzle (Problem) by James Pate Williams, Jr.
Most of the six algorithms were developed back in the years 1999 to 2001 when I was a Master of Software Engineering and Doctoral candidate at Auburn University. Professor Gerry V. Dozier was my Master research advisor. The algorithms developed were in alphabetical order:
- Arc-Consistency 3
- Arc-Consistency 4
- Backjump
- Backmark
- Chronological Backtracking
- Evolutionary Hill-Climber (My algorithm)
The first five algorithms were stated in pseudocode in the excellent treatise Foundations of Constraint Satisfaction by Edward Tsang. Below are six runs of my test C++ application (Win32 Console App) using 8 queens and 50 samples.
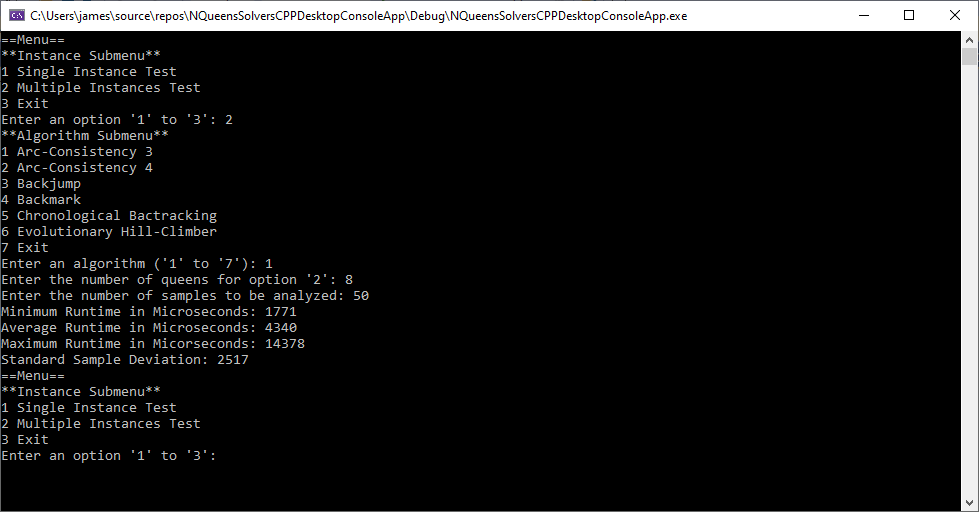
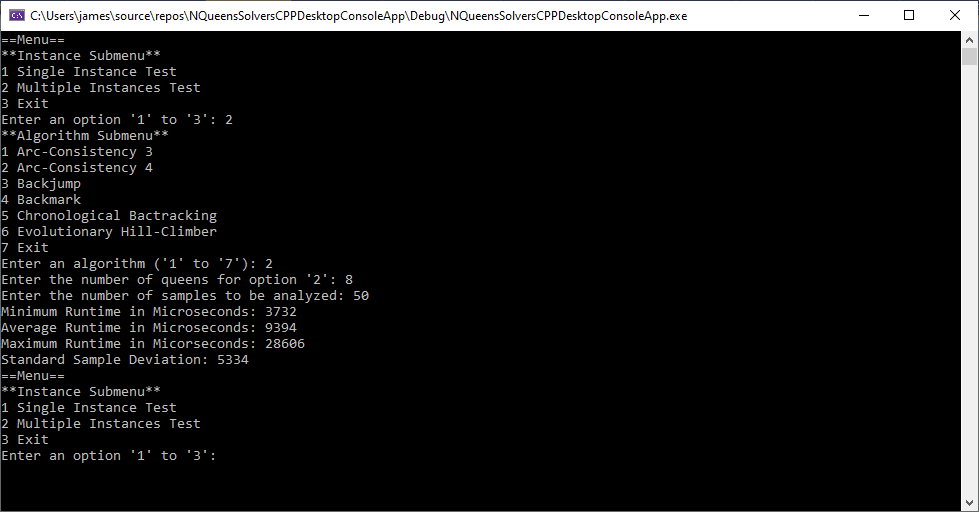
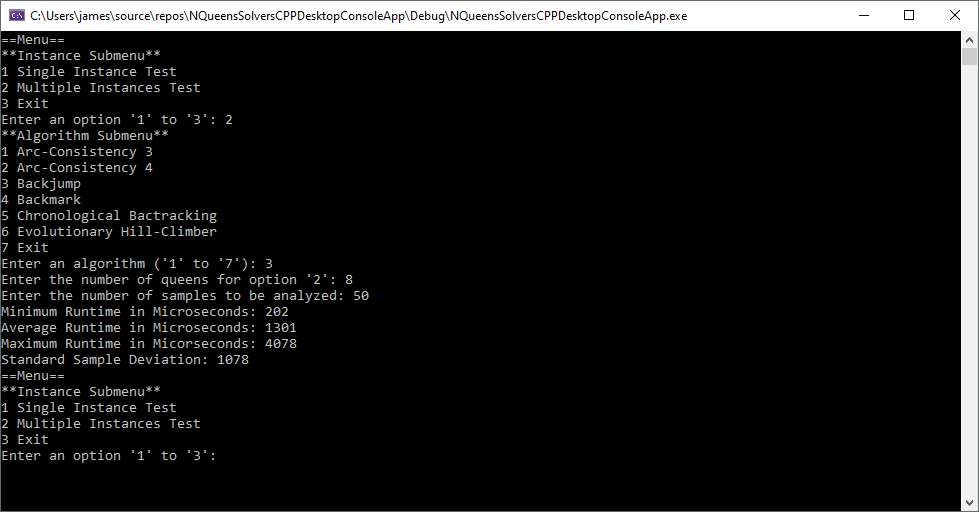
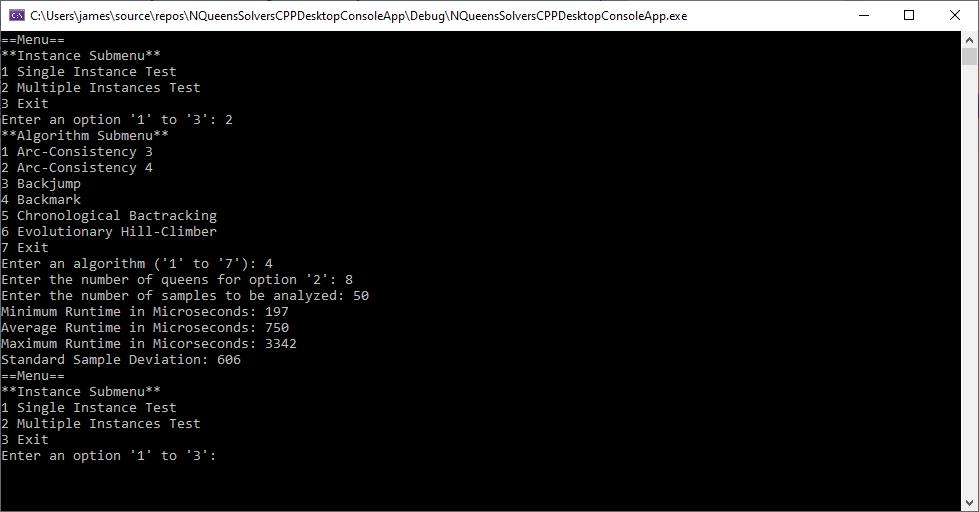
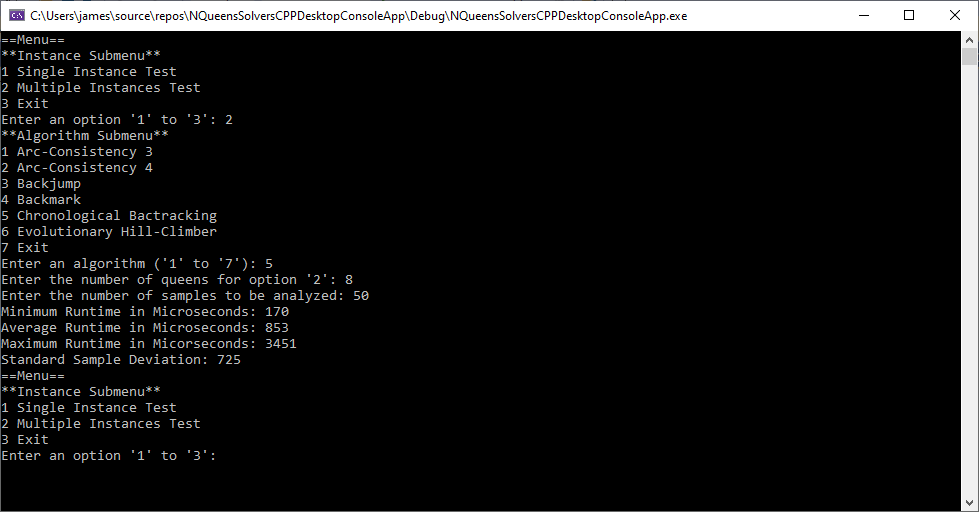
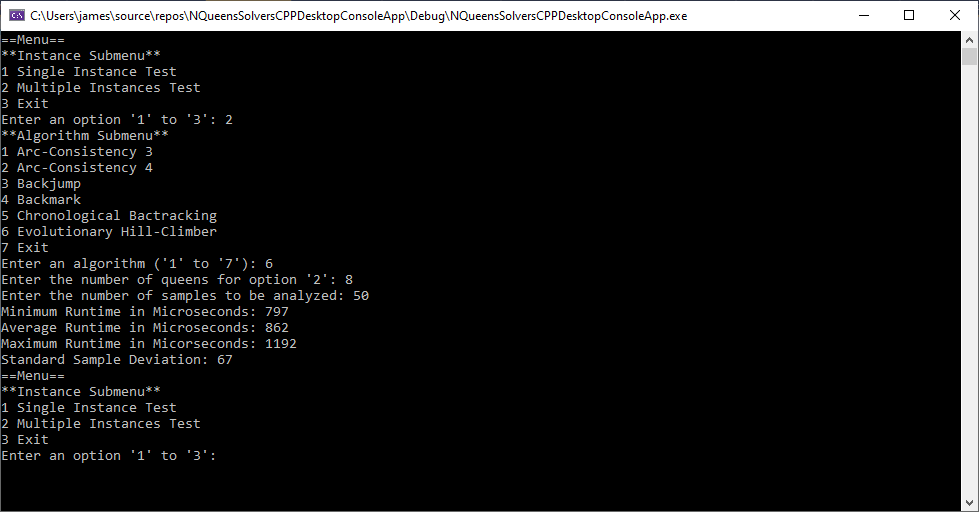
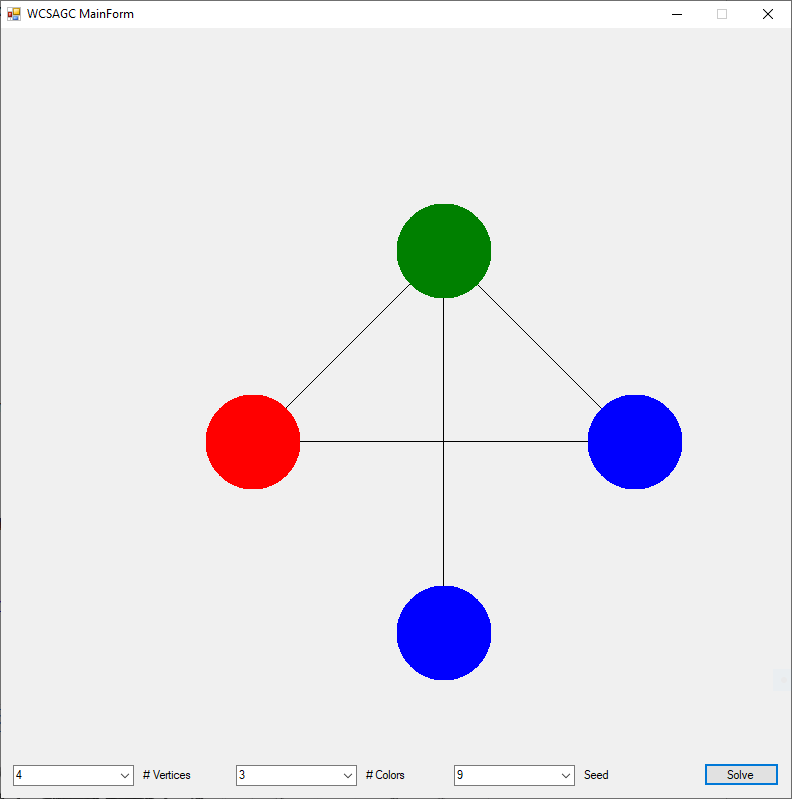
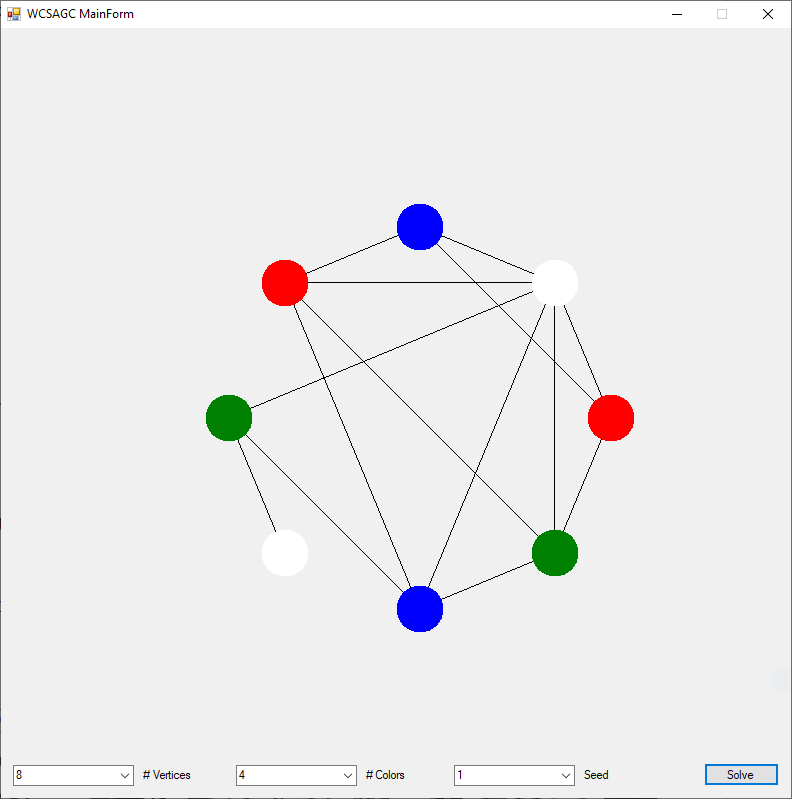
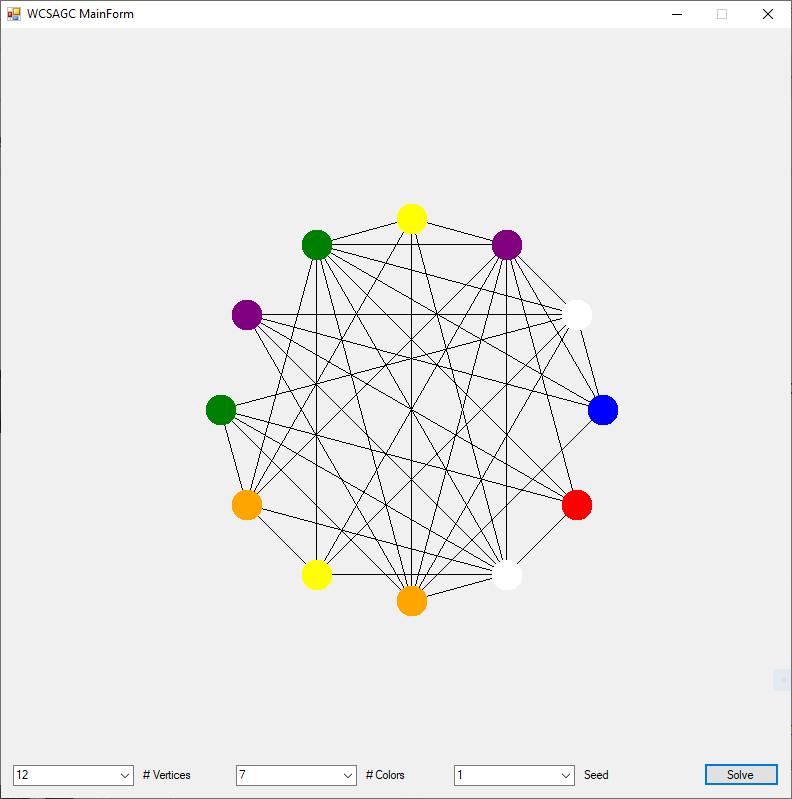
The Graph Coloring Problem by James Pate Williams, Jr.
The Graph Coloring Problem and N-Queens Puzzle are both NP-Complete constraint satisfaction problems. There does not exist polynomial time algorithms to solve large instances of either problem. The Graph Coloring Problem is given a graph of n-vertices and m-edges find the minimum number of colors such that no two connected vertices are of the same color. The N-Queens Puzzle is given a n-by-n chessboard and n-queens place the queens such that no two queens are attacking one another. A queen in chess can move any number of squares diagonally, horizontally, or vertically.
As a Master of Software Engineering graduate student in the era 1998 to 2000, I majored in the subdiscipline of artificial intelligence known as constraint satisfaction. I developed evolutionary hill-climbing algorithms to solve constraint satisfaction problems. I specifically solved instances of the Graph Coloring Problem and the N-Queens Puzzle. I compared my algorithms with other researchers’ algorithms. One of the algorithms tested was Makato Yokoo’s Weak-Commitment Search Algorithm (WCSA). Yakoo wrote a very nice book named “Distributed Constraint Satisfaction” which has excellent flow-charts of several algorithms including the Min-Conflicts Search Algorithm (MCSA) and his WCSA. I implemented both algorithms in the C++ and Java computer languages.
I rewrote the preceding two algorithms in the C# computer language sometime in the epoch 2008 – 2009. Below are three instances of the Graph Coloring Problem with four, eight, and twelve vertices solved by the Yakoo’s WCSA.