Category: Cryptanalysis
Some More C Multiple Quadratic Polynomial Sieve Factoring Results, C/C++ SHA-1 Results, and C# SHA-3 Results © Monday, August 17, 2026, by James Pate Williams, Jr.
Blog Entry © Wednesday, August 12, 2026, by James Pate Williams, Jr., Two Brute Force Elliptic Curve Point Counting Algorithms
Blog Entry © Tuesday, June 16, 2026, by James Pate Williams, Jr., More 64-Bit Pseudoprimes Found Using John Pollard’s Factoring with Cubic Integers
Blog Entry © Wednesday, June 4, 2025, Differential Cryptanalysis of DES by James Pate Williams, Jr.
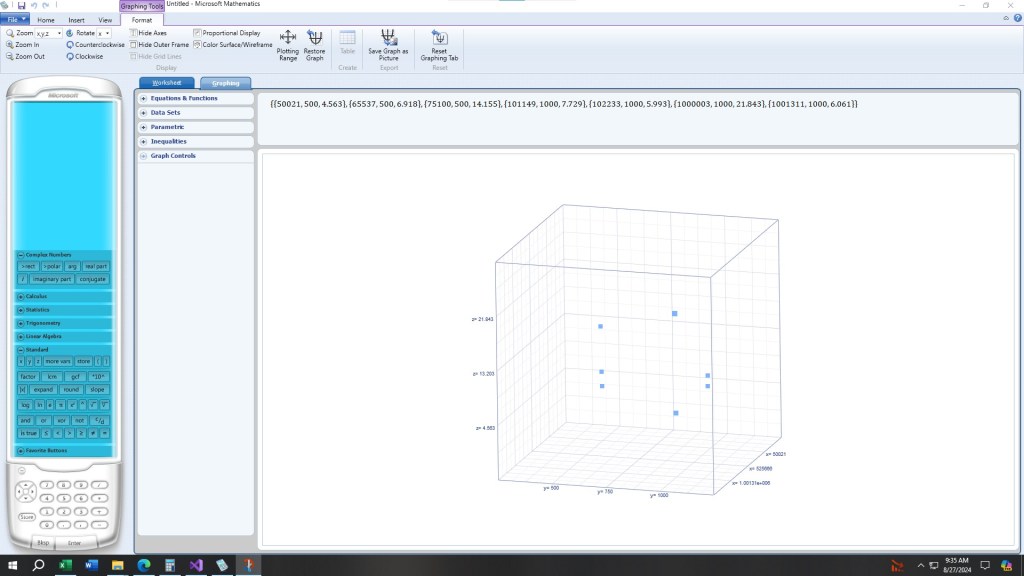
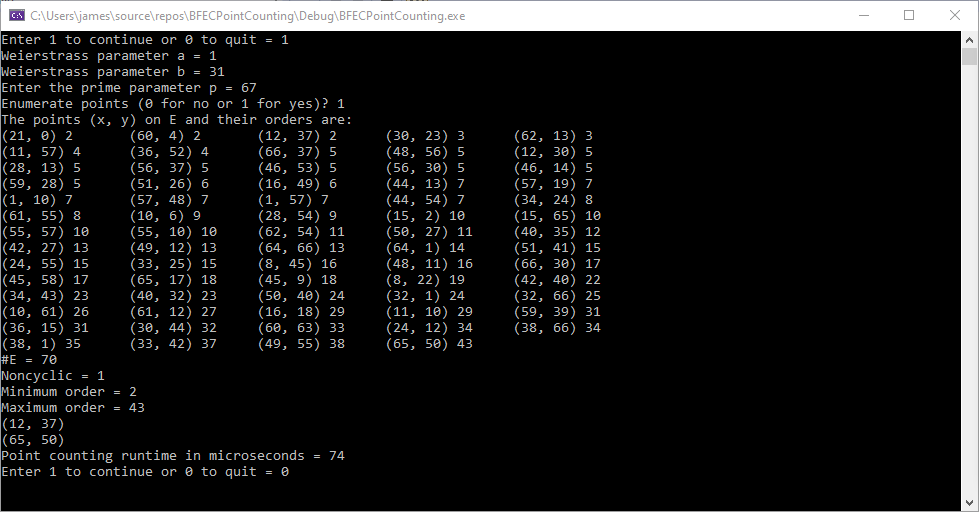
Below are outputs from three different apps perform differential cryptanalysis on three, four, and six round DES algorithms. Three round is first etc.
E = 007e0e80 680c0000
E* = bf02ac05 40520000
C' = 965d5b67
E = a0bff415 02f60000
E* = 8a6a5ebf 28aa0000
C' = 9c9c1f56
E = ef15068f 695f0000
E* = 05e9a2bf 56040000
C' = d575db2b
1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0
0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 3
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 1 0 3 0 0 1 0 0 1 0 0 0 0
0 1 0 0 0 2 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 1 0 1 0 0 0 1 0
0 0 1 1 0 0 0 0 1 0 1 0 2 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0
0 0 0 3 0 0 0 0 0 0 0 0 0 0 1 1
0 2 0 0 0 0 0 0 0 0 0 0 1 1 0 0
0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0
3 1 0 0 0 0 0 0 0 0 2 2 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0 1 0 1 1
1 1 1 0 1 0 0 0 0 1 1 1 0 0 1 0
0 0 0 0 1 1 0 0 0 0 0 0 0 0 2 1
0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0
0 0 0 0 2 0 0 0 3 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 2 0 0 0 0 0 0 1 0 0 0 0 2 0
1 0 0 1 1 0 0 3 0 0 0 0 1 0 0 1
0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0
1 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0
0 0 2 1 0 1 0 3 0 0 0 1 1 0 0 0
0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1
0 0 2 0 0 0 2 0 0 0 0 1 2 1 1 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1
0 3 0 0 0 0 1 0 0 0 0 0 0 0 0 0
47 05 19 00 24 07 07 49
J = bc54c060 71f10000
key = 0001101P0110001P01?01?0P1?00100P0101001P0000??0P111?11?P?100011P
88
Unknown bit count = 8
key = 0001101001100010010011001000100101010010000011011110110001000110
key = 1a624c89 520dec46
E = f069a40a a8a70000
E* = c0e9f28f 810f0000
C' = fa719d15
E = dabefbef 01a70000
E* = c03fa95f 29570000
C' = ea5605a1
E = ca7d095a 815f0000
E* = d57d094a 800f0000
C' = 0b00c0cb
E = 7fbf56aa 43050000
E* = 65945eba 55550000
C' = 0923cbd6
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0
2 0 2 1 1 0 0 0 2 1 0 0 1 0 0 0
1 0 0 1 1 0 0 2 0 1 0 1 0 0 0 2
4 1 1 0 2 0 1 0 1 1 1 0 1 0 1 0
1 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0
1 1 2 1 1 1 1 2 3 2 1 2 1 1 2 1
1 1 2 1 1 1 1 2 1 2 2 1 1 2 1 2
2 3 1 1 4 2 2 2 1 1 1 1 2 2 1 1
1 2 1 1 1 2 1 1 1 1 1 1 1 1 2 2
1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1
1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1
1 1 1 2 2 4 1 1 1 1 2 1 2 2 1 2
1 1 1 2 1 2 1 2 1 2 1 1 2 1 1 1
0 1 1 0 0 0 1 0 0 1 0 0 1 1 1 0
0 1 0 1 0 0 0 1 2 0 1 0 3 0 1 0
4 0 1 1 2 1 1 0 0 0 1 1 1 0 0 2
2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 2 1 2 1 1 1 1 1 1 1 1 2 4 1 2
1 1 1 1 1 1 1 1 1 1 2 2 1 2 1 3
1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1
1 2 1 2 3 1 3 1 1 1 1 1 1 1 1 1
1 0 2 2 0 0 0 1 0 2 1 0 2 0 0 0
1 1 0 0 0 1 0 0 0 1 4 1 0 0 0 1
1 1 1 0 0 2 0 1 0 0 1 0 1 0 0 0
0 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0 4 2 1 1 1 0
0 0 0 0 0 0 0 1 0 0 3 2 0 1 0 1
1 0 1 1 1 0 1 0 0 0 2 0 0 1 0 0
0 0 0 1 0 0 0 1 0 0 2 0 0 1 0 1
00 32 36 37 32 13 26 10
J = 02092580 d68a0000
key = 10?10?0P???1101P0011000P0000??0P00??01?P??00100P?101000P11?0101P
Unknown bit Count = 14
7774
key = 1001010011111011001100010000000100100110110010001101000011001011
key = 94fb3101 26c8d0cb
Plaintext-Ciphertext Pairs:
0 748502cd 38451097 03c70306 d8a09f10
0 38747564 38451097 78560a09 60e6d4cb
1 48691102 6acdff31 45fa285b e5adc730
1 375bd31f 6acdff31 134f7915 ac253457
2 357418da 013fec86 d8a31b2f 28bbc5cf
2 12549847 013fec86 0f317ac2 b23cb944
Possible J Values:
J # J Cnt J-Value(s):
0 1 47
1 1 5
2 1 19
3 1 0
4 1 24
5 1 7
6 1 7
7 1 49
key = 0001101001100010010011001000100101010010000011011110110001000110
tst = 0001101001100010010011001000100101010010000011011110110001000110
key = 1a624c89 520dec46
tst = 1a624c89 520dec46
J # J-Value True J-Value:
0 47 47
1 5 5
2 19 19
3 0 0
4 24 24
5 7 7
6 7 7
7 49 49
Tested Keys # = 1073
Runtime (s) = 0
Runtime per test (s) = 0.000028
Runtime max estimated (s) = 0.029784
Blog Entry (c) Tuesday, August 27, 2024, Graphing New Goldwasser-Kilian Primality Test Results by James Pate Williams, Jr.
The x -axis is the number to be tested, the y-axis is prime number bound for factoring, and the z-axis is the runtime in seconds.
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. New and Improved Version of the Goldwasser-Kilian Primality Test
I corrected my powering modulo a prime routine. I added Pollard’s p – 1 factoring method and Shanks-Mestre elliptic curve point counting algorithm.
number to be tested or 0 to quit:
10000019
number of primes in factor base:
10000
Prime sieving time = 3.220000
N[0] = 10000019
a = 7838973
b = 2449531
m = 9995356
q = 356977
P = (9786147, 3226544)
P1 = (0, 1)
P2 = (5887862, 8051455)
N[1] = 356977
a = 45561
b = 178451
m = 357946
q = 178973
P = (80627, 163299)
P1 = (0, 1)
P2 = (52101, 282559)
N[2] = 178973
a = 135281
b = 76426
m = 178996
q = 73
P = (10238, 98035)
P1 = (0, 1)
P2 = (46702, 94326)
number is proven prime
runtime in seconds = 35.471000
number to be tested or 0 to quit:
10015969
number of primes in factor base:
10000
Prime sieving time = 3.424000
N[0] = 10015969
a = 6613193
b = 3951715
m = 10013908
q = 2503477
P = (998314, 8329764)
P1 = (0, 1)
P2 = (6944357, 1053776)
N[1] = 2503477
a = 1175442
b = 379813
m = 2505736
q = 293
P = (646462, 1631861)
P1 = (0, 1)
P2 = (1477980, 88719)
number is proven prime
runtime in seconds = 5.612000
number to be tested or 0 to quit:
99997981
number of primes in factor base:
10000
Prime sieving time = 4.152000
N[0] = 99997981
a = 34129462
b = 80482974
m = 100001414
q = 181
P = (19305995, 40493835)
P1 = (0, 1)
P2 = (33828245, 72969559)
number is proven prime
runtime in seconds = 11.500000
number to be tested or 0 to quit:
100001819
number of primes in factor base:
100000
Prime sieving time = 3.218000
N[0] = 100001819
a = 2694060
b = 17329746
m = 100008102
q = 5569
P = (124594, 14596756)
P1 = (0, 1)
P2 = (32514144, 56926555)
number is proven prime
runtime in seconds = 76.301000
number to be tested or 0 to quit:
100005317
number of primes in factor base:
100000
Prime sieving time = 3.269000
N[0] = 100005317
a = 45478318
b = 328034
m = 99988256
q = 3124633
P = (62548529, 30179124)
P1 = (0, 1)
P2 = (70379514, 76899689)
N[1] = 3124633
a = 2605576
b = 1809212
m = 3127654
q = 503
P = (1236288, 2081401)
P1 = (0, 1)
P2 = (2264479, 2583693)
number is proven prime
runtime in seconds = 459.979000
number to be tested or 0 to quit:
100000007
number of primes in factor base:
100000
Prime sieving time = 3.209000
N[0] = 100000007
a = 50593669
b = 72502607
m = 100005736
q = 2053
P = (72365335, 69885097)
P1 = (0, 1)
P2 = (55023241, 20078454)
number is proven prime
runtime in seconds = 163.705000
number to be tested or 0 to quit:
100014437
number of primes in factor base:
100000
Prime sieving time = 3.919000
N[0] = 100014437
a = 49955472
b = 45482796
m = 100024160
q = 263
P = (41650735, 8652103)
P1 = (0, 1)
P2 = (53790105, 37282431)
number is proven prime
runtime in seconds = 12.915000
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. Single Precision (64-Bit) Version of Pollard’s P-1 Factoring Method
prime number sieve creation
time in seconds = 3.483000
number to be factored or 0 to quit:
2111222333
1 11 1 p
2 17 1 p
3 11289959 1 p
factoring time in seconds = 0.063000
number to be factored or 0 to quit:
1234567890
1 2 1 p
2 3 2 p
3 5 1 p
4 3607 1 p
5 3803 1 p
factoring time in seconds = 0.133000
number to be factored or 0 to quit:
2^30+0
prime powers are not allowed
number to be factored or 0 to quit:
0
Numerical Explorations 