Category: Cubic Integers
Blog Entry (c) Tuesday September 3, 2024, by James Pate Williams, Jr.
Preliminary Factorization Results of the Thirteenth Fermat Number (c) February 5, 2024, by James Pate Williams, Jr.
I am working on a factorization of the Thirteenth Fermat number which is 2 ^ 8192 + 1 and is 2,467 decimal digits in length. I am using Pollard’s factoring with cubic integers on the number (2 ^ 2731) ^ 3 + 2. I am also utilizing a homegrown variant of the venerable Pollard and Brent rho method and Arjen K. Lenstra’s Free LIP Elliptic Curve Method. I can factor the seventh Fermat number 2 ^ 128 + 1 in five to thirty minutes using my C# code. The factoring with cubic integers code is in C and uses Free-LIP.
Fermat factoring status (prothsearch.com)
The following is a run of Lenstra’s ECM algorithm:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^8192+1
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 1
2710954639361 p # digits 13
3603109844542291969 p # digits 19
Runtime (s) = 17015.344000
I aborted the previous computation due to the fact I was curious about the number of prime factors that could be found on personal computer. I will try a lot more calculation time in a future run. My homegrown application is able to at least find the first factor of Fermat Number 13.
Latest Factoring Results (c) February 4, 2024, by James Pate Williams, Jr.
I am testing two factoring algorithms: Pollard-Shor-Williams’s method, a home-grown version of the venerable Pollard rho algorithm and Pollard’s factoring with cubic integers. The second recipe is from “The Development of the Number Field Sieve” edited by Arjen K. Lenstra and Hendrik W. Lenstra, Jr. I use the 20-digit test number, 2 ^ 66 + 2 = 73786976294838206466. My method is very fast with this number as shown below:
2^66+2
73786976294838206466 20
Pseudo-Random Number Generator Seed = 1
Number of Tasks = 1
2 p 1
3 p 1
11 p 2
131 p 3
2731 p 4
409891 p 6
7623851 p 7
Elapsed hrs:min:sec.MS = 00:00:00.652
Function Evaluations = 1995
The Pollard factoring with cubic integers takes a long time but is capable of factoring much larger numbers. The results of the full factorization of my test number are:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^66+2
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 3
73786976294838206466
Enter a lower bound : -50000
Enter a upper bound : +50000
Enter b lower bound : +1
Enter b upper bound : +50000
Enter maximum kernels : 1024
Enter algebraic prime count: 300
Enter rational prime count: 300
Enter lo large prime bound: 10000
Enter hi large prime bound: 11000
Numbers sieved = 452239293
Successes 0 gcd(a, b) is 1 = 274929004
Successes 1 rational smooth a + b * r = 181838258
Successes 2 long long smooth = 68959
Successes 3 kernels tested = 535
2 p # digits 1
3 p # digits 1
11 p # digits 2
131 p # digits 3
2731 p # digits 4
409891 p # digits 6
7623851 p # digits 7
Runtime (s) = 36383.696000
It took over ten hours to fully factor, 2 ^ 66 + 2. I am currently attempting to factor the Thirteenth Fermat number which is 2 ^ (2 ^ 13) + 1 = 2 ^ 8192 + 1. The number has 2,467 decimal digits. I am using 399 algebraic prime numbers, 600 rational prime numbers, and 316 “large prime numbers” (primes between 12,000 and 15,000). I have to find the kernels of a 1316 by 1315 matrix. I am trying the factorization using a maximum of 8192 kernels. I suspect this computation will take about a week on my desktop workstation. There is no guarantee that I will find a non-trivial factor of 2 * (2731 ^ 3) + 2.
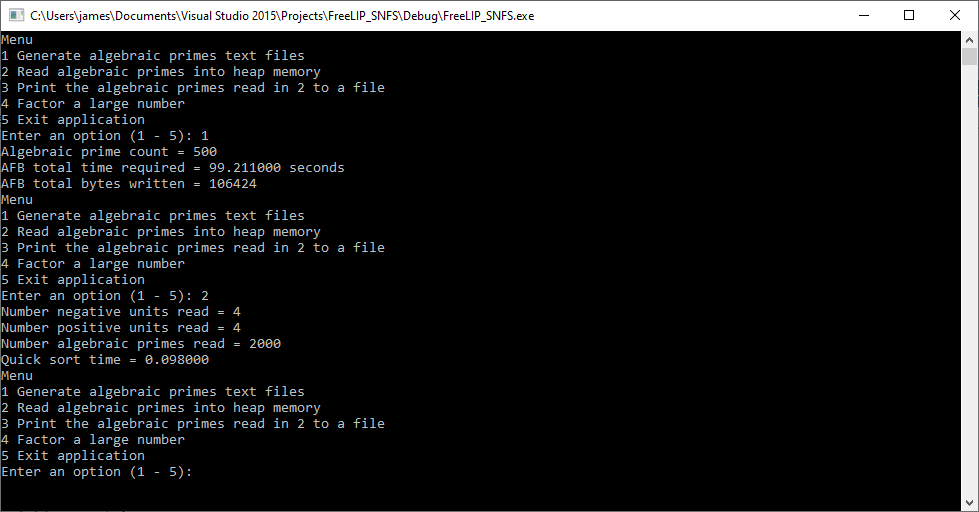
Latest Software Development Project Started on Saturday, October 15, 2022, 12:07:19 AM by James Pate Williams, Jr.
I am in the progress of translating (porting) my J. M. Pollard’s algorithm “Factoring with Cubic Integers” C# application to a Free LIP based vanilla C Windows 32-bit console application. The first phase of the method is to generate two factor bases namely a rational prime factor base and an algebraic integer prime factor base. I have included some preliminary results from this fast-moving computer programming task. I generated 2012 algebraic integer primes in about a minute and thirty seconds.

No Allies and None on the Horizon by James Pate Williams, Jr., BA, BS, MSwE, PhD
An ally is an entity (person, country, etc.) that is willing to share your sacrifices and possibly fight and die in your causes. I have no allies now nor probably in the foreseeable future. If I had allies, they would boycott the businesses, etc. that have ejected or rejected me. I have a pretty large list of businesses that have exercised their local not United States right to bar me from their place of work. The list is below:
- International House of Pancakes
- Lafayette Arms Motel located near 1.
- Gus’ Grille
- Dixie Donuts
- Golden Bike Shop
- First United Methodist Church of LaGrange, Georgia (they took away my rights to volunteer for the untaxed organization)
- Waffle House on New Franklin Road
- Waffle House on Lafayette Parkway
- Walmart Super Center and Perhaps Elsewhere at Walmart Stores
The United States is losing its natural and acquired allies with its chaotic foreign policy.
Cubic Integers
The following text is based upon Appendix 5 “Higher Algebraic Number Fields” found in the book “Prime Numbers and Computer Methods for Factorization” by Hans Riesel. Cubic integers are algebraic numbers of the form [a, b, c] which is a short hand for a + b * z + c * z * z where z is the cube root of -2. we have z * z * z = z ^ 3 = -2 and z ^ 4 = -2 * z. The numbers a, b, and c are rational integers in Z. The product of two cubic integers is also a cubic integer (expansion of equation A5.8):
[a, b, c] * [d, e, f] = (a + b * z + c * z * z) * (d + e * z + f * z * z) = a * d + a * e * z + a * f * z * z + b * d * z + b * e * z * z + b * f * z * z * z + c * d * z * z + c * e * z * z * z + c * f * z * z * z * z = a * d – 2 * b * f – 2 * c * e + (a * e + b * d – 2 * c * f) * z + (a * f + b * e + c * d) * z * z = [ a * d – 2 * b * f – 2 * c * e , a * e + b * d – 2 * c * f , a * f + b * e + c * d ]
The defining equation for z is z^3 + 2 = 0. The other two roots of the polynomial f(z) = z^3 + 2 are the complex conjugates z[2] = z * (-1 + i * SQR(3)) / 2 and z[3] = z * (-1 – i * SQR(3)) / 2, where SQR(x) is the square root function such that x = SQR(x) * SQR(x) and i = SQR(-1), the imaginary unit. z[2] and z[3] are complex numbers of the form w = u + i * v, where u is the real part and v is the imaginary part. Let o = (-1 + i * SQR(3)) / 2. z[2] = o * z and z[3] = o * o * z.
Q(z) is a field and the integers of the field form Z(z) which is a ring. The norm of the cubic integer [a, b, c] is (expansion of equation A5.7):
N[a, b, c] = (a + b * z + c * z * z) * (a + b * o * z + c * o * o * z * z) * (a + b * o * o * z + c * o * z * z) = a ^ 3 – 2b ^ 3 + 4 * c ^ 3 + 6 * a * b * c
I wrote a computer application in C# to recreate the results of Appendix 5. Below is a screen shot of the application’s form:
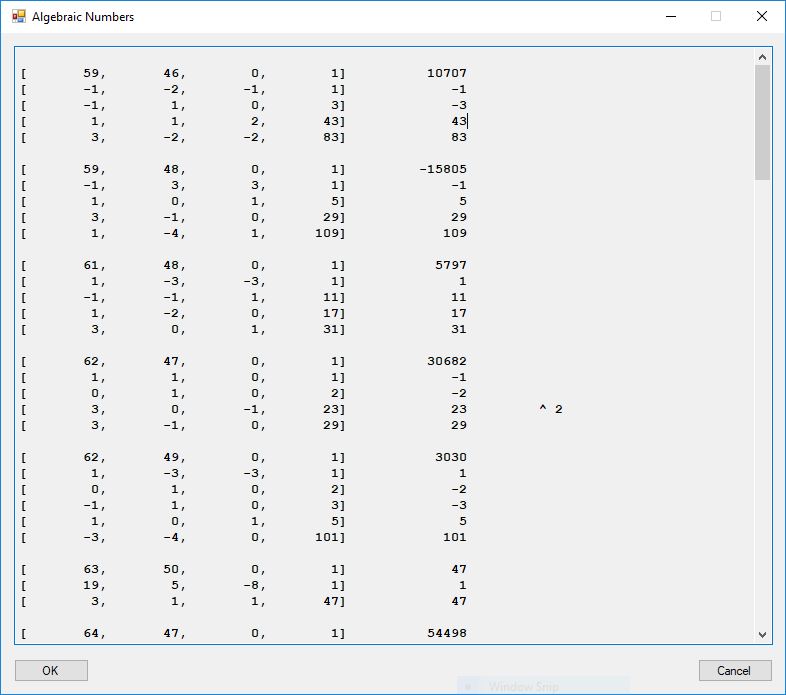
I reproduce the units table of page 300 below:
Positive Units
[ 1, 0, 0, 1] 1
[ 1, 1, 0, 1] -1
[ 1, 2, 1, 1] 1
[ -1, 3, 3, 1] -1
[ -7, 2, 6, 1] 1
[ -19, -5, 8, 1] -1
[ -35, -24, 3, 1] 1
[ -41, -59, -21, 1] -1
[ 1, -100, -80, 1] 1
[ 161, -99, -180, 1] -1
[ 521, 62, -279, 1] 1
[ 1079, 583, -217, 1] -1
[ 1513, 1662, 366, 1] 1
Negative Units
[ -1, 0, 0, -1] -1
[ -1, 1, -1, -1] -1
[ 5, -4, 3, -1] 1
[ -19, 15, -12, -1] -1
[ 73, -58, 46, -1] 1
[ -281, 223, -177, -1] -1
[ 1081, -858, 681, -1] 1
[ -4159, 3301, -2620, -1] -1
[ 16001, -12700, 10080, -1] 1
[ -61561, 48861, -38781, -1] -1
[ 236845, -187984, 149203, -1] 1
[ -911219, 723235, -574032, -1] -1
[ 3505753, -2782518, 2208486, -1] 1
The pertinent factorization of the cubic integer prime numbers less than 300 are given next:
Case 1
[ 1, 0, 1, 5] 5
[ -1, -1, 1, 11] 11
[ 1, -2, 0, 17] 17
[ 3, 0, -1, 23] 23
[ 3, -1, 0, 29] 29
[ 1, -3, 1, 41] 41
[ 3, 1, 1, 47] 47
[ -1, -3, 0, 53] 53
[ 3, 0, 2, 59] 59
[ -1, -2, 2, 71] 71
[ 3, -2, -2, 83] 83
[ 1, -2, 3, 89] 89
[ -3, -4, 0, 101] 101
[ -1, 0, 3, 107] 107
[ 1, -4, 2, 113] 113
[ 3, -3, -1, 131] 131
[ -3, -1, 3, 137] 137
[ 1, -4, -1, 149] 149
[ -3, -3, 2, 167] 167
[ 3, -5, 4, 173] 173
[ 5, -3, 0, 179] 179
[ -1, 2, 4, 191] 191
[ 5, -2, -1, 197] 197
[ 3, 2, 3, 227] 227
[ 5, 0, 3, 233] 233
[ 1, -3, 4, 239] 239
[ 1, -5, 0, 251] 251
[ 1, 0, 4, 257] 257
[ 3, -4, -3, 263] 263
[ 1, -5, 3, 269] 269
[ -1, -1, 4, 281] 281
[ -3, -6, -1, 293] 293
Case 2
[ -1, 0, 2, 31] 31
[ 3, 0, 1, 31] 31
[ -1, -2, 1, 31] 31
[ 1, 1, 2, 43] 43
[ 3, -1, -1, 43] 43
[ 3, -2, 0, 43] 43
[ 1, 0, 3, 109] 109
[ 1, -4, 1, 109] 109
[ 5, 2, 0, 109] 109
[ -1, -4, 0, 127] 127
[ -1, -1, 3, 127] 127
[ 5, -1, 0, 127] 127
[ 5, 1, 1, 157] 157
[ 5, 0, 2, 157] 157
[ 3, -3, -2, 157] 157
[ 3, -4, -1, 223] 223
[ -3, -5, 0, 223] 223
[ 1, -5, 2, 223] 223
[ -1, 1, 4, 229] 229
[ -3, 0, 4, 229] 229
[ 5, -2, -2, 229] 229
[ 1, -5, -1, 277] 277
[ 3, -5, 0, 277] 277
[ -3, -4, 2, 277] 277
[ -1, -5, 1, 283] 283
[ 3, 0, 4, 283] 283
[ 5, 3, 2, 283] 283
Case 3
[ 0, 1, 0, 2] -2
Case 4
[ -1, 1, 0, 3] -3
I reproduce the factorization of the norms of [a, b, 0] found on page 303 are given below:
[ 59, 46, 0, 1] 10707
[ -1, -2, -1, 1] -1
[ -1, 1, 0, 3] -3
[ 1, 1, 2, 43] 43
[ 3, -2, -2, 83] 83
[ 59, 48, 0, 1] -15805
[ -1, 3, 3, 1] -1
[ 1, 0, 1, 5] 5
[ 3, -1, 0, 29] 29
[ 1, -4, 1, 109] 109
[ 61, 48, 0, 1] 5797
[ 1, -3, -3, 1] 1
[ -1, -1, 1, 11] 11
[ 1, -2, 0, 17] 17
[ 3, 0, 1, 31] 31
[ 62, 47, 0, 1] 30682
[ 1, 1, 0, 1] -1
[ 0, 1, 0, 2] -2
[ 3, 0, -1, 23] 23 ^ 2
[ 3, -1, 0, 29] 29
[ 62, 49, 0, 1] 3030
[ 1, -3, -3, 1] 1
[ 0, 1, 0, 2] -2
[ -1, 1, 0, 3] -3
[ 1, 0, 1, 5] 5
[ -3, -4, 0, 101] 101
[ 63, 50, 0, 1] 47
[ 19, 5, -8, 1] 1
[ 3, 1, 1, 47] 47
[ 64, 47, 0, 1] 54498
[ -1, -1, 0, 1] 1
[ 0, 1, 0, 2] -2
[ -1, 1, 0, 3] -3
[ -1, 0, 2, 31] 31
[ -3, -6, -1, 293] 293
[ 65, 53, 0, 1] -23129
[ 1, 1, 0, 1] -1
[ -3, -4, 0, 101] 101
[ -3, 0, 4, 229] 229
[ 66, 53, 0, 1] -10258
[ 1, 2, 1, 1] 1
[ 0, 1, 0, 2] -2
[ 3, 0, -1, 23] 23
[ 3, -4, -1, 223] 223
[ 67, 53, 0, 1] 3009
[ 7, -2, -6, 1] -1
[ -1, 1, 0, 3] -3
[ 1, -2, 0, 17] 17
[ 3, 0, 2, 59] 59
[ 1693, 749, 0, 1] 4012180059
[ -1, -2, -1, 1] -1
[ -1, 1, 0, 3] -3
[ 3, -2, 0, 43] 43
[ 5, 0, 2, 157] 157
[ 7, -3, 0, 397] 397
[ 5, 1, 4, 499] 499
The last factorization is from “The Development of the Number Field Sieve” edited by A. K. Lenstra and H. W. Lenstra, Jr. containing the paper “Factoring with Cubic Integers” by J. M. Pollard page 10.