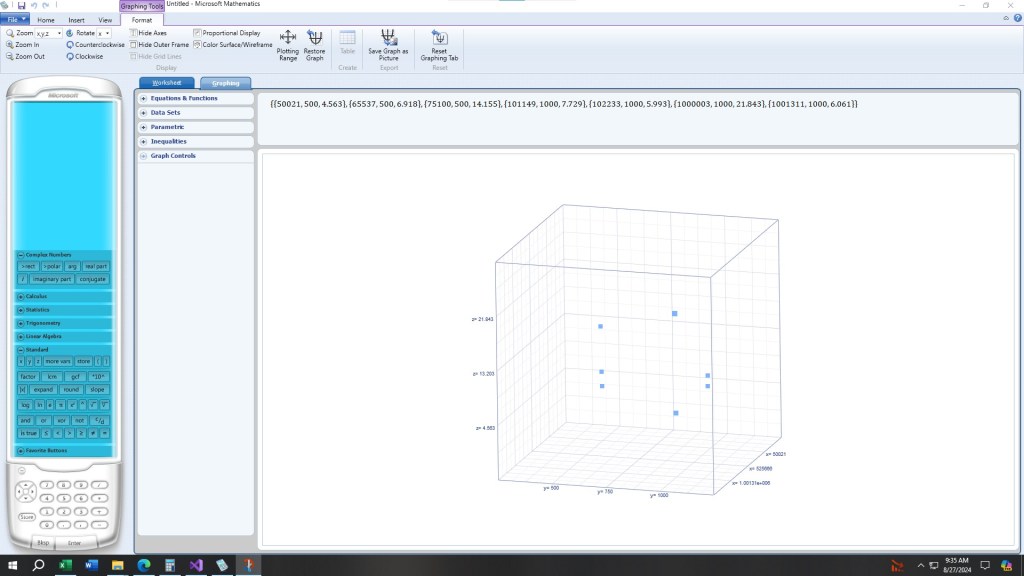
The x -axis is the number to be tested, the y-axis is prime number bound for factoring, and the z-axis is the runtime in seconds.
I corrected my powering modulo a prime routine. I added Pollard’s p – 1 factoring method and Shanks-Mestre elliptic curve point counting algorithm.
number to be tested or 0 to quit:
10000019
number of primes in factor base:
10000
Prime sieving time = 3.220000
N[0] = 10000019
a = 7838973
b = 2449531
m = 9995356
q = 356977
P = (9786147, 3226544)
P1 = (0, 1)
P2 = (5887862, 8051455)
N[1] = 356977
a = 45561
b = 178451
m = 357946
q = 178973
P = (80627, 163299)
P1 = (0, 1)
P2 = (52101, 282559)
N[2] = 178973
a = 135281
b = 76426
m = 178996
q = 73
P = (10238, 98035)
P1 = (0, 1)
P2 = (46702, 94326)
number is proven prime
runtime in seconds = 35.471000
number to be tested or 0 to quit:
10015969
number of primes in factor base:
10000
Prime sieving time = 3.424000
N[0] = 10015969
a = 6613193
b = 3951715
m = 10013908
q = 2503477
P = (998314, 8329764)
P1 = (0, 1)
P2 = (6944357, 1053776)
N[1] = 2503477
a = 1175442
b = 379813
m = 2505736
q = 293
P = (646462, 1631861)
P1 = (0, 1)
P2 = (1477980, 88719)
number is proven prime
runtime in seconds = 5.612000
number to be tested or 0 to quit:
99997981
number of primes in factor base:
10000
Prime sieving time = 4.152000
N[0] = 99997981
a = 34129462
b = 80482974
m = 100001414
q = 181
P = (19305995, 40493835)
P1 = (0, 1)
P2 = (33828245, 72969559)
number is proven prime
runtime in seconds = 11.500000
number to be tested or 0 to quit:
100001819
number of primes in factor base:
100000
Prime sieving time = 3.218000
N[0] = 100001819
a = 2694060
b = 17329746
m = 100008102
q = 5569
P = (124594, 14596756)
P1 = (0, 1)
P2 = (32514144, 56926555)
number is proven prime
runtime in seconds = 76.301000
number to be tested or 0 to quit:
100005317
number of primes in factor base:
100000
Prime sieving time = 3.269000
N[0] = 100005317
a = 45478318
b = 328034
m = 99988256
q = 3124633
P = (62548529, 30179124)
P1 = (0, 1)
P2 = (70379514, 76899689)
N[1] = 3124633
a = 2605576
b = 1809212
m = 3127654
q = 503
P = (1236288, 2081401)
P1 = (0, 1)
P2 = (2264479, 2583693)
number is proven prime
runtime in seconds = 459.979000
number to be tested or 0 to quit:
100000007
number of primes in factor base:
100000
Prime sieving time = 3.209000
N[0] = 100000007
a = 50593669
b = 72502607
m = 100005736
q = 2053
P = (72365335, 69885097)
P1 = (0, 1)
P2 = (55023241, 20078454)
number is proven prime
runtime in seconds = 163.705000
number to be tested or 0 to quit:
100014437
number of primes in factor base:
100000
Prime sieving time = 3.919000
N[0] = 100014437
a = 49955472
b = 45482796
m = 100024160
q = 263
P = (41650735, 8652103)
P1 = (0, 1)
P2 = (53790105, 37282431)
number is proven prime
runtime in seconds = 12.915000
prime number sieve creation
time in seconds = 3.483000
number to be factored or 0 to quit:
2111222333
1 11 1 p
2 17 1 p
3 11289959 1 p
factoring time in seconds = 0.063000
number to be factored or 0 to quit:
1234567890
1 2 1 p
2 3 2 p
3 5 1 p
4 3607 1 p
5 3803 1 p
factoring time in seconds = 0.133000
number to be factored or 0 to quit:
2^30+0
prime powers are not allowed
number to be factored or 0 to quit:
0
The Goldwasser-Kilian Primality proving algorithm was the first method to utilize elliptic curves to generate primality proving certificates. What follows is a file of two certificates and the single precision C source code.
The problem is to find the real root of the equation: f(x)=x^(x^8)-8=0. I use the Newton-Raphson method, a root finding algorithm. A first guess is x = 2. The solution is: x = 1.2968395547, f(x) = -2.6645353e-15. I compute the necessary derivative using central-finite differences with a step size of h = 2/10000.
degree (0 to quit) = 5
a[5] = 1
a[4] = -15.5
a[3] = 77.5
a[2] = -155
a[1] = 124
a[0] = -32
x[0] = 0.45
x[1] = 0.9
x[2] = 1.8
x[3] = 3.6
x[4] = 7.2
iterations = 31
root[0] = 5.0000000000e-01
root[1] = 1.0000000000e+00
root[2] = 2.0000000000e+00
root[3] = 4.0000000000e+00
root[4] = 8.0000000000e+00
func[0] = 0.0000000000e+00
func[1] = 0.0000000000e+00
func[2] = 0.0000000000e+00
func[3] = 0.0000000000e+00
func[4] = 0.0000000000e+00
degree (0 to quit) =
Numerical Explorations 