Category: Numerical Analysis
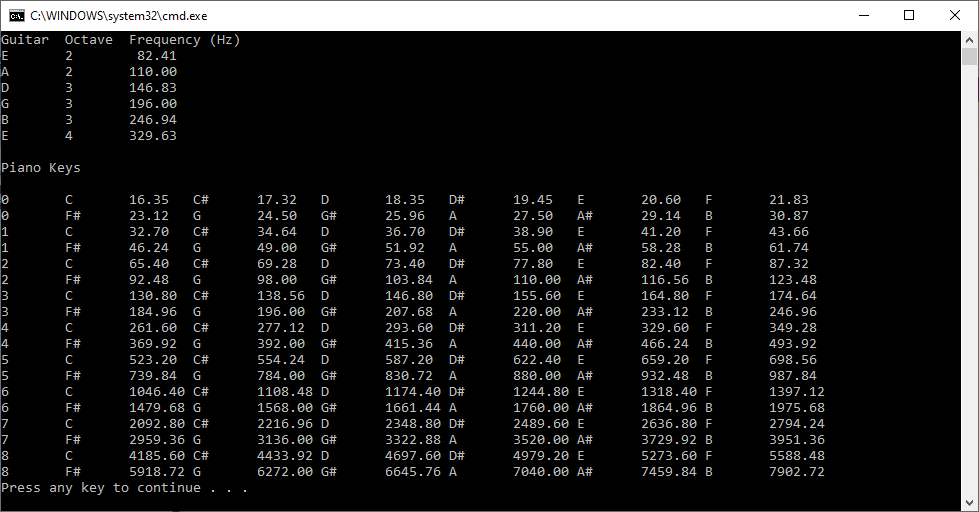
Guitar String and Piano Key Frequencies by James Pate Williams, Jr.
// FrequencyKey.cpp : Defines the entry point for the console application.
// James Pate Willims, Jr. (c) All Applicable Rights Reserved
#include "stdafx.h"
#include <math.h>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<string> pnote;
double a = pow(2.0, 1.0 / 12.0);
double f0 = 440.0, gStrF[6];
double e2, a2, d3, g3, b3, e4;
double pfreq[9 * 12];
int offset = 0;
double fn(int n)
{
return f0 * pow(a, n);
}
void printFrequency(char note, int octave, double frequency)
{
cout << note << "\t" << octave << "\t";
cout << setw(6) << fixed << setprecision(2);
cout << frequency << endl;
}
int main()
{
for (int octave = 0; octave <= 8; octave++)
{
pnote.push_back("C");
pnote.push_back("C#");
pnote.push_back("D");
pnote.push_back("D#");
pnote.push_back("E");
pnote.push_back("F");
pnote.push_back("F#");
pnote.push_back("G");
pnote.push_back("G#");
pnote.push_back("A");
pnote.push_back("A#");
pnote.push_back("B");
}
pfreq[0] = 16.35;
pfreq[1] = 17.32;
pfreq[2] = 18.35;
pfreq[3] = 19.45;
pfreq[4] = 20.6;
pfreq[5] = 21.83;
pfreq[6] = 23.12;
pfreq[7] = 24.5;
pfreq[8] = 25.96;
pfreq[9] = 27.5;
pfreq[10] = 29.14;
pfreq[11] = 30.87;
for (int octave = 1; octave <= 8; octave++)
{
for (int i = 0; i < 12; i++)
{
pfreq[octave * 12 + i] = 2.0 * pfreq[(octave - 1) * 12 + i];
}
}
gStrF[0] = e2 = fn(offset - 29);
gStrF[1] = a2 = fn(offset - 24);
gStrF[2] = d3 = fn(offset - 19);
gStrF[3] = g3 = fn(offset - 14);
gStrF[4] = b3 = fn(offset - 10);
gStrF[5] = e4 = fn(offset - 5);
cout << "Guitar\tOctave\tFrequency (Hz)" << endl;
printFrequency('E', 2, e2);
printFrequency('A', 2, a2);
printFrequency('D', 3, d3);
printFrequency('G', 3, g3);
printFrequency('B', 3, b3);
printFrequency('E', 4, e4);
cout << endl;
cout << "Piano Keys" << endl << endl;
for (int octave = 0; octave <= 8; octave++)
{
for (int i = 0; i < 2; i++)
{
cout << octave << '\t';
for (int j = 0; j < 6; j++)
{
{
cout << pnote[(12 * octave + 6 * i + j) % 12] << '\t';
cout << pfreq[(12 * octave + 6 * i + j)] << '\t';
}
}
cout << endl;
}
}
return 0;
}
C# Three-Dimensional Cartesian Vector Calculator (c) September 24, 2023, by James Pate Williams, Jr. All Applicable Rights Reserved
I wrote and debugged this C# code after I found out that my 1989 vector calculator in Modula-2 for the Commadore Amiga 2000 was not working correctly.
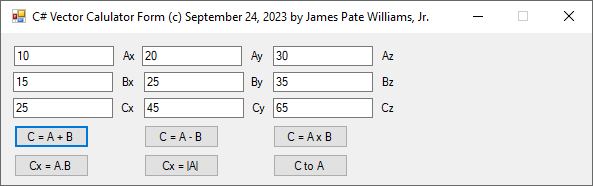
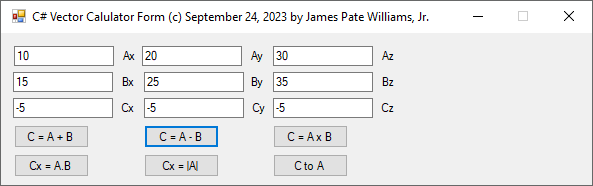
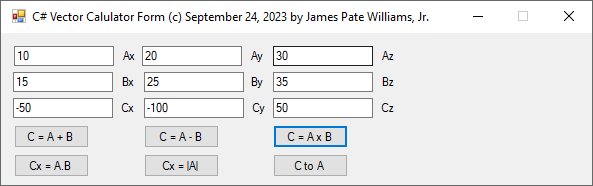
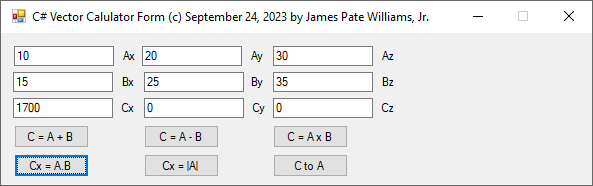
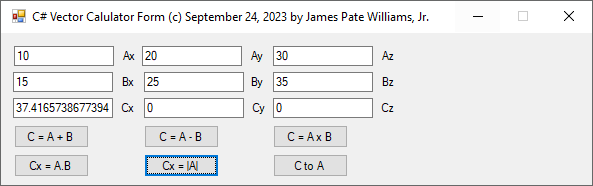
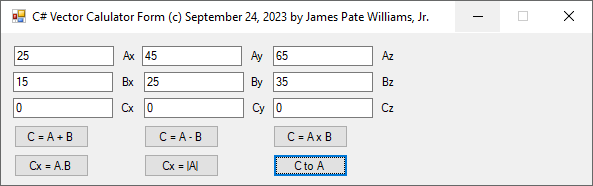
// C# Three-Dimensional Cartesian Vector Calculator
// (c) September 24, 2023 by James Pate Williams, Jr.
// All Applicable Rights Reserved
using System;
using System.Windows.Forms;
namespace CSVectorCalculator
{
public partial class MainForm : Form
{
public MainForm()
{
InitializeComponent();
}
private static double[] A = new double[3];
private static double[] B = new double[3];
private static double[] C = new double[3];
private void ValidateAB(
ref bool valid)
{
try
{
A[0] = double.Parse(textBox1.Text);
A[1] = double.Parse(textBox2.Text);
A[2] = double.Parse(textBox3.Text);
B[0] = double.Parse(textBox4.Text);
B[1] = double.Parse(textBox5.Text);
B[2] = double.Parse(textBox6.Text);
valid = true;
}
catch (Exception ex)
{
MessageBox.Show(ex.Message, "Warning",
MessageBoxButtons.OK, MessageBoxIcon.Warning);
valid = false;
}
}
private void FillC(double[] C)
{
textBox7.Text = C[0].ToString();
textBox8.Text = C[1].ToString();
textBox9.Text = C[2].ToString();
}
private void button1_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] + B[0];
C[1] = A[1] + B[1];
C[2] = A[2] + B[2];
FillC(C);
}
}
private void button2_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] - B[0];
C[1] = A[1] - B[1];
C[2] = A[2] - B[2];
FillC(C);
}
}
private void button3_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[1] * B[2] - A[2] * B[1];
C[1] = A[0] * B[2] - A[2] * B[0];
C[2] = A[1] * B[0] - A[0] * B[1];
FillC(C);
}
}
private void button4_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = A[0] * B[0] + A[1] * B[1] + A[2] * B[2];
C[1] = C[2] = 0.0;
FillC(C);
}
}
private void button5_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
C[0] = Math.Sqrt(A[0] * A[0] + A[1] * A[1] + A[2] * A[2]);
C[1] = C[2] = 0.0;
FillC(C);
}
}
private void button6_Click(object sender, EventArgs e)
{
bool valid = true;
ValidateAB(ref valid);
if (valid)
{
textBox1.Text = C[0].ToString();
textBox2.Text = C[1].ToString();
textBox3.Text = C[2].ToString();
C[0] = C[1] = C[2] = 0.0;
FillC(C);
}
}
}
}
Two of Kepler’s Three Laws of Planetary Motion by James Pate Williams, Jr.
Java Bessel Function Application by James Pate Williams, Jr.
Comparison of Aitkin Extrapolation and Newton’s Method to Compute Square Roots by James Pate Williams, Jr.
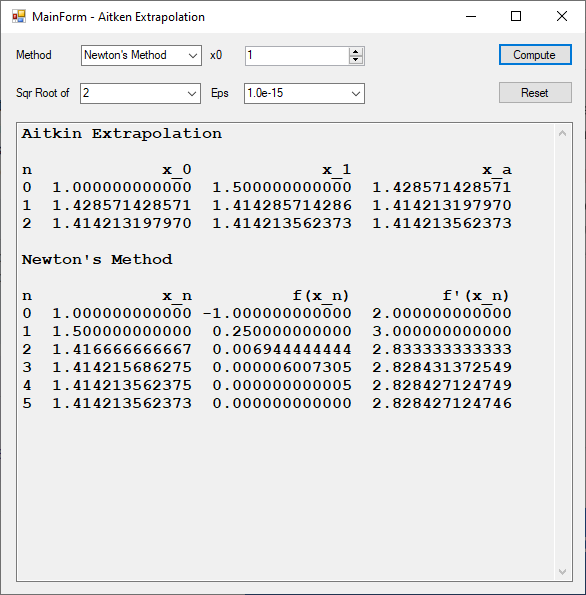

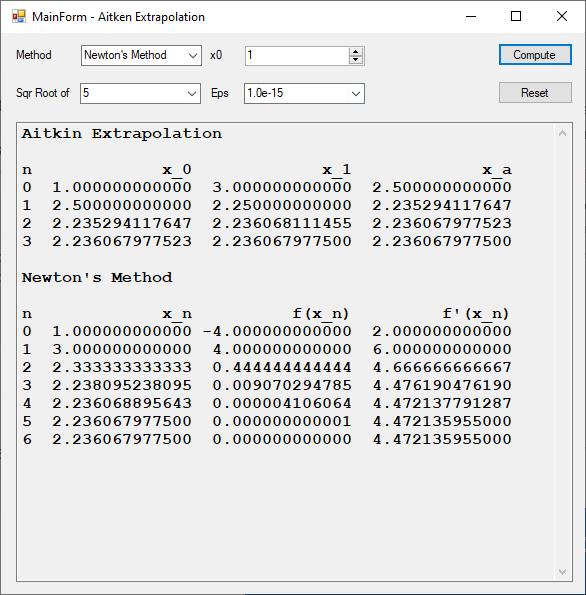

Comparison of Linear Systems Applications in C# and C++ by James Pate Williams, Jr.
Back in 2017 I created a C# application that implemented the direct methods: Cholesky decomposition, Gaussian elimination with partial pivoting, LU decomposition, and simple Gaussian elimination. The classical iterative methods Gauss-Seidel, Jacobi, Successive Overrelaxation, and gradient descent were also implemented along with the modern iterative methods: conjugate gradient descent and Modified Richardson’s method. Recently I translated the C# code to C++. I used the following test matrices: Cauchy, Lehmer, Pascal, and other. Below are some results. As is apparent the C++ runtimes are faster than the C# execution times.
Richardson Method Translated from C Source Code to C# by James Pate Williams, Jr.


The Richardson Method is called before eliminating the system of linear equations.
Added elimination results from a vanilla C program and a C# application.


These results are not in total agreement with H. T. Lau’s results.
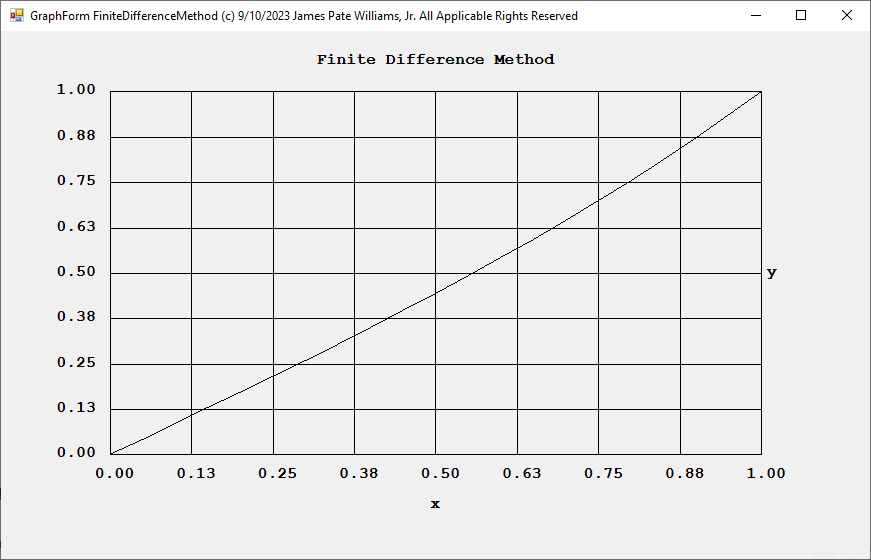
Finite Difference Method for Solving Second Order Ordinary Differential Equations by James Pate Williams, Jr.
My reference is Numerical Analysis: An Algorithmic Approach 3rd Edition by S. D. Conte and Carl de Boor Chapter 9.1.
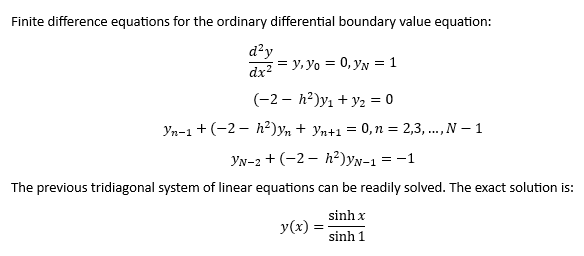


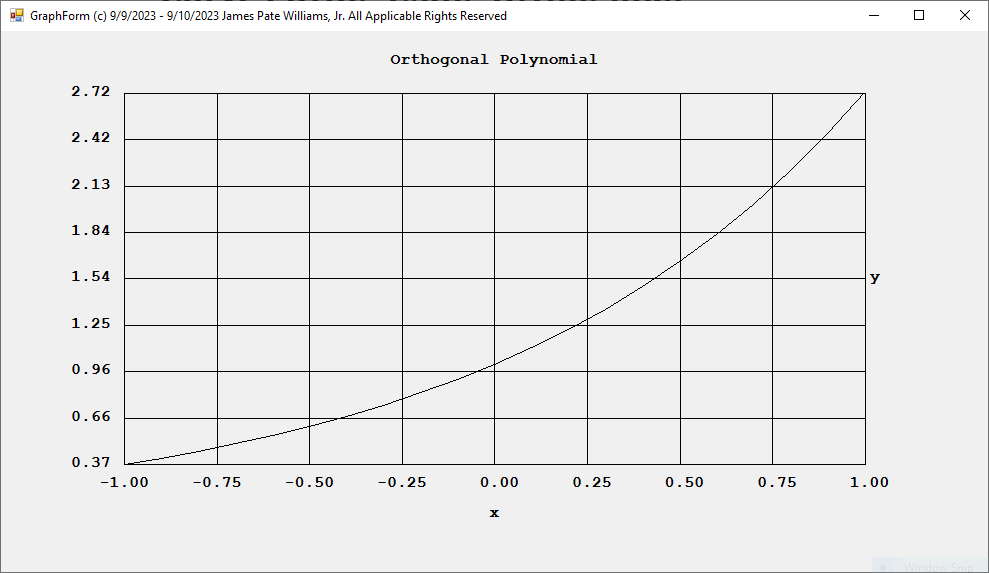
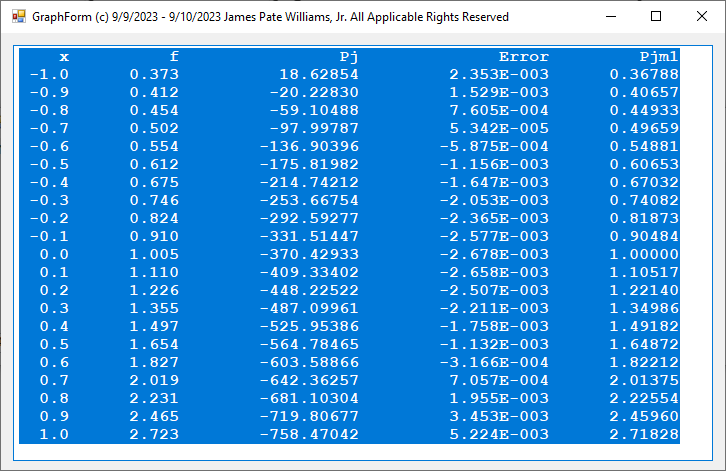
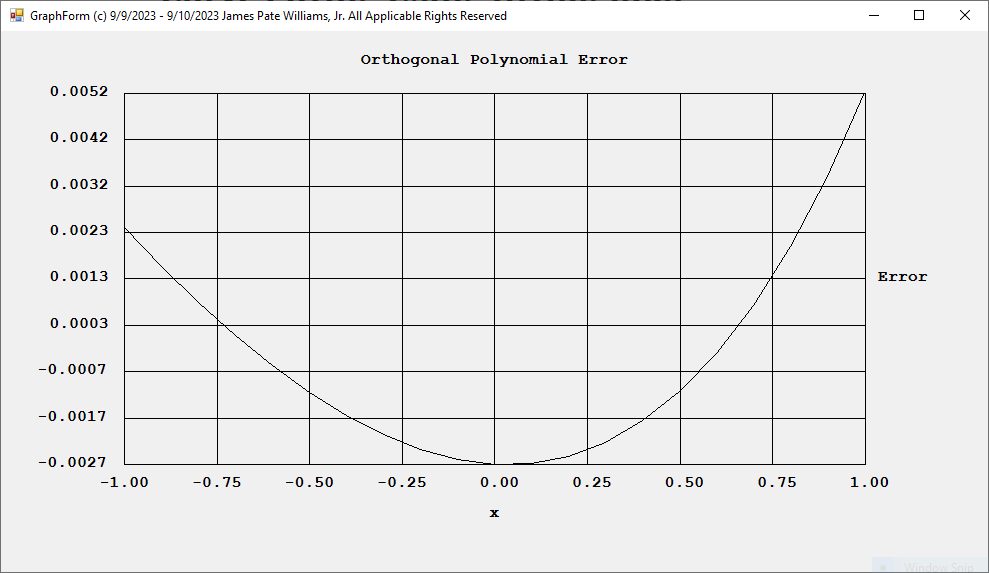
Curve Fitting Using Orthogonal Polynomials in C# by James Pate Williams, Jr.
The curve in this best fit example is the function y(x) = exp(x).