Category: Primality Test
Blog Entry © Wednesday, October 15, 2025, by James Pate Williams, Jr. Miscellaneous Algorithms from Chapters 2 and 4 of the “Handbook of Applied Cryptography” by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone
#pragma once
class PrimalityTests
{
public:
static int Jacobi(long long a, long long n);
static void LongLongToBits(
long long n, std::vector<int>& bits);
static long long ModPow(
long long a, long long k, long long n);
static bool MillerRabin(long long n, int t);
static bool SolovayStrassen(long long n, int t);
};
#include "pch.h"
#include "PrimalityTests.h"
int PrimalityTests::Jacobi(long long a, long long n) {
int s;
long long a1, b = a, e = 0, m, n1;
if (a == 0)
return 0;
if (a == 1)
return 1;
while ((b & 1) == 0)
b >>= 1, e++;
a1 = b;
m = n % 8;
if (!(e & 1))
s = +1;
else if (m == 1 || m == 7)
s = +1;
else if (m == 3 || m == 5)
s = -1;
if (n % 4 == 3 && a1 % 4 == 3)
s = -s;
if (a1 != 1)
n1 = n % a1;
else
n1 = 1;
return s * Jacobi(n1, a1);
}
void PrimalityTests::LongLongToBits(
long long n, std::vector<int>& bits) {
bits.clear();
while (n > 0) {
int digit = (int)(n % 2);
bits.push_back(digit);
n /= 2;
}
}
long long PrimalityTests::ModPow(
long long a, long long k, long long n) {
std::vector<int> kBits;
LongLongToBits(k, kBits);
long long b = 1;
if (k == 0) {
return b;
}
long long A = a;
if (kBits[0] == 1) {
b = a;
}
for (int i = 1; i < (int)kBits.size(); i++) {
A = (A * A) % n;
if (kBits[i] == 1) {
b = (A * b) % n;
}
}
return b;
}
bool PrimalityTests::MillerRabin(long long n, int t) {
if (n == 2 || n == 3) {
return true;
}
long long m = n % 2;
if (m == 0) {
return false;
}
long long n2 = n - 2;
std::random_device rd; // Seed generator
std::mt19937 mt(rd()); // Mersenne Twister engine
std::uniform_int_distribution<long long> dist(2, n2);
long long n1 = n - 1;
long long r = n1;
long s = 0;
m = r % 2;
while (m == 0) {
r = r / 2;
m = r % 2;
s++;
}
for (int i = 1; i <= t; i++) {
long long a = dist(mt);
long long y = ModPow(a, r, n);
if (y != 1 && y != n1) {
int j = 1;
while (j <= s && y != n1) {
y = ModPow(y, 2, n);
if (y == 1)
return false;
j++;
}
if (y != n1)
return false;
}
}
return true;
}
bool PrimalityTests::SolovayStrassen(long long n, int t) {
long long n1 = n - 1, n2 = n - 2, n12 = n1 / 2;
std::random_device rd; // Seed generator
std::mt19937 mt(rd()); // Mersenne Twister engine
std::uniform_int_distribution<long long> dist(2, n2);
for (int i = 1; i <= t; i++) {
long long a = dist(mt);
long long r = ModPow(a, n12, n);
if (r != 1 && r != n1)
return false;
int s = Jacobi(a, n);
if (!(r == s) && !(s == -1 && r == n1))
return false;
}
return true;
}
// ProbPrimalityTests.cpp (c) Monday, October 13, 2025
// Reference: "Handbook of Applied Cryptography" by
// Alfred J. Menezes, Paul C. van Oorschot, Scott A.
// Vanstone Chapters 2, 3, and 4
// https://www.walter-fendt.de/html5/men/primenumbers_en.htm
#include "pch.h"
int main()
{
while (true) {
std::string str = "";
std::cout << "== Menu ==" << std::endl;
std::cout << "1 Test Jacobi" << std::endl;
std::cout << "2 Test To Bits" << std::endl;
std::cout << "3 Test ModPow" << std::endl;
std::cout << "4 Test Miller-Rabin" << std::endl;
std::cout << "5 Test Solovay-Strassen" << std::endl;
std::cout << "6 Exit" << std::endl;
std::cout << "Option (1 - 6): ";
std::getline(std::cin, str);
int option = std::stoi(str);
if (option < 1 || option > 6) {
std::cout << "Illegal option" << std::endl;
continue;
}
if (option == 6) {
break;
}
switch (option) {
case 1: {
std::cout << "a = ";
std::getline(std::cin, str);
long long a = std::stoll(str);
std::cout << "n = ";
std::getline(std::cin, str);
long long n = std::stoll(str);
int j = PrimalityTests::Jacobi(a, n);
std::cout << "Jacobi = " << j << std::endl;
break;
}
case 2: {
std::vector<int> bits = { };
std::cout << "n = ";
std::getline(std::cin, str);
long long n = std::stoll(str);
PrimalityTests::LongLongToBits(n, bits);
for (int i = (int)bits.size() - 1; i >= 0; i--) {
std::cout << bits[i];
}
std::cout << std::endl;
break;
}
case 3: {
std::cout << "a = ";
std::getline(std::cin, str);
long long a = std::stoll(str);
std::cout << "k = ";
std::getline(std::cin, str);
long long k = std::stoll(str);
std::cout << "n = ";
std::getline(std::cin, str);
long long n = std::stoll(str);
long long m = PrimalityTests::ModPow(a, k, n);
std::cout << "ModPow(a, k, n) = " << m << std::endl;
break;
}
case 4: {
std::cout << "n = ";
std::getline(std::cin, str);
long long n = std::stoll(str);
std::cout << "t = ";
std::getline(std::cin, str);
int t = std::stoi(str);
bool mr = PrimalityTests::MillerRabin(n, t);
std::cout << "Miller-Rabin = " << mr << std::endl;
break;
}
case 5: {
std::cout << "n = ";
std::getline(std::cin, str);
long long n = std::stoll(str);
std::cout << "t = ";
std::getline(std::cin, str);
int t = std::stoi(str);
bool ss = PrimalityTests::SolovayStrassen(n, t);
std::cout << "Solavay-Strassen = " << ss << std::endl;
break;
}
}
}
return 0;
}
// pch.h: This is a precompiled header file.
// Files listed below are compiled only once, improving build performance for future builds.
// This also affects IntelliSense performance, including code completion and many code browsing features.
// However, files listed here are ALL re-compiled if any one of them is updated between builds.
// Do not add files here that you will be updating frequently as this negates the performance advantage.
#ifndef PCH_H
#define PCH_H
#include <iostream>
#include <random>
#include <string>
#include <vector>
#include "framework.h"
#include "PrimalityTests.h"
#endif //PCH_H
Blog Entry (c) Tuesday, August 27, 2024, Graphing New Goldwasser-Kilian Primality Test Results by James Pate Williams, Jr.
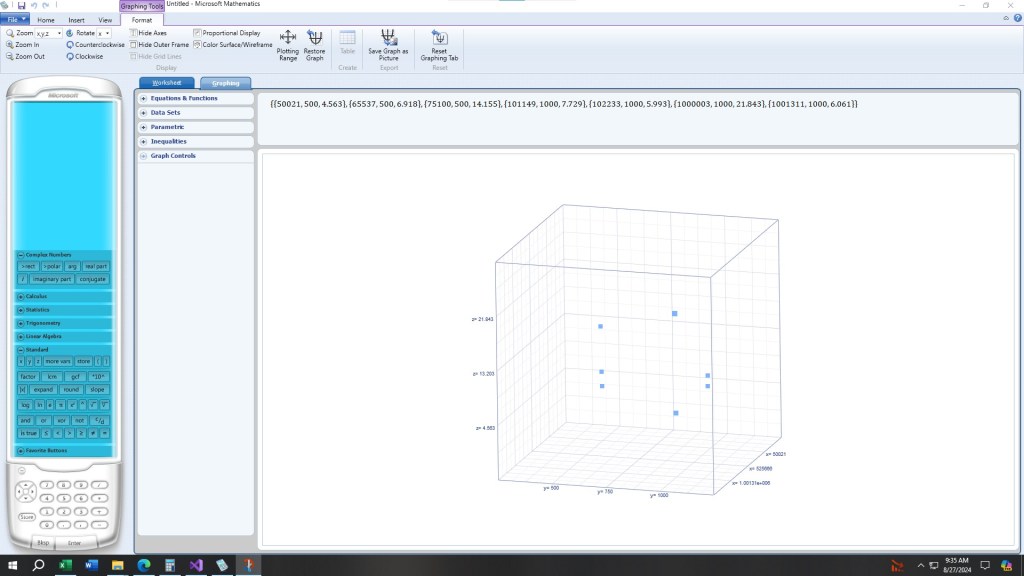
The x -axis is the number to be tested, the y-axis is prime number bound for factoring, and the z-axis is the runtime in seconds.
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. New and Improved Version of the Goldwasser-Kilian Primality Test
I corrected my powering modulo a prime routine. I added Pollard’s p – 1 factoring method and Shanks-Mestre elliptic curve point counting algorithm.
number to be tested or 0 to quit:
10000019
number of primes in factor base:
10000
Prime sieving time = 3.220000
N[0] = 10000019
a = 7838973
b = 2449531
m = 9995356
q = 356977
P = (9786147, 3226544)
P1 = (0, 1)
P2 = (5887862, 8051455)
N[1] = 356977
a = 45561
b = 178451
m = 357946
q = 178973
P = (80627, 163299)
P1 = (0, 1)
P2 = (52101, 282559)
N[2] = 178973
a = 135281
b = 76426
m = 178996
q = 73
P = (10238, 98035)
P1 = (0, 1)
P2 = (46702, 94326)
number is proven prime
runtime in seconds = 35.471000
number to be tested or 0 to quit:
10015969
number of primes in factor base:
10000
Prime sieving time = 3.424000
N[0] = 10015969
a = 6613193
b = 3951715
m = 10013908
q = 2503477
P = (998314, 8329764)
P1 = (0, 1)
P2 = (6944357, 1053776)
N[1] = 2503477
a = 1175442
b = 379813
m = 2505736
q = 293
P = (646462, 1631861)
P1 = (0, 1)
P2 = (1477980, 88719)
number is proven prime
runtime in seconds = 5.612000
number to be tested or 0 to quit:
99997981
number of primes in factor base:
10000
Prime sieving time = 4.152000
N[0] = 99997981
a = 34129462
b = 80482974
m = 100001414
q = 181
P = (19305995, 40493835)
P1 = (0, 1)
P2 = (33828245, 72969559)
number is proven prime
runtime in seconds = 11.500000
number to be tested or 0 to quit:
100001819
number of primes in factor base:
100000
Prime sieving time = 3.218000
N[0] = 100001819
a = 2694060
b = 17329746
m = 100008102
q = 5569
P = (124594, 14596756)
P1 = (0, 1)
P2 = (32514144, 56926555)
number is proven prime
runtime in seconds = 76.301000
number to be tested or 0 to quit:
100005317
number of primes in factor base:
100000
Prime sieving time = 3.269000
N[0] = 100005317
a = 45478318
b = 328034
m = 99988256
q = 3124633
P = (62548529, 30179124)
P1 = (0, 1)
P2 = (70379514, 76899689)
N[1] = 3124633
a = 2605576
b = 1809212
m = 3127654
q = 503
P = (1236288, 2081401)
P1 = (0, 1)
P2 = (2264479, 2583693)
number is proven prime
runtime in seconds = 459.979000
number to be tested or 0 to quit:
100000007
number of primes in factor base:
100000
Prime sieving time = 3.209000
N[0] = 100000007
a = 50593669
b = 72502607
m = 100005736
q = 2053
P = (72365335, 69885097)
P1 = (0, 1)
P2 = (55023241, 20078454)
number is proven prime
runtime in seconds = 163.705000
number to be tested or 0 to quit:
100014437
number of primes in factor base:
100000
Prime sieving time = 3.919000
N[0] = 100014437
a = 49955472
b = 45482796
m = 100024160
q = 263
P = (41650735, 8652103)
P1 = (0, 1)
P2 = (53790105, 37282431)
number is proven prime
runtime in seconds = 12.915000
Blog Entry (c) Monday, August 19, 2024, by James Pate Williams, Jr. Results from a Corrected Version of my Implementation of the 64-Bit Goldwasser-Kilian Primality Test
Blog Entry Wednesday, August 14, 2024 (c) James Pate Williams, Jr. Goldwasser-Kilian Primality Test
The Goldwasser-Kilian Primality proving algorithm was the first method to utilize elliptic curves to generate primality proving certificates. What follows is a file of two certificates and the single precision C source code.
Blog Entry Wednesday, July 10, 2024, © James Pate Williams, Jr. My Dual Interests in Cryptography and Number Theory
I became fascinated with secret key cryptography as a child. Later, as an adult, in around 1979, I started creating crude symmetric cryptographic algorithms. I became further enthralled with cryptography and number theory in 1996 upon reading Applied Cryptography, Second Edition: Protocols, Algorithms, and Source Code in C by Bruce Schneier and later the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone. After implementing many of the algorithms in both tomes, I communicated my results to two of the authors namely Bruce Schneier and Professor Alfred J. Menezes. In 1997 I developed a website devoted to constraint satisfaction problems and their solutions, cryptography, and number theory. I posted legal C and C++ source code. Professor Menezes advertised my website along with his treatise. See the following blurb:

In the spirit of my twin scientific infatuations, I offer yet another C integer factoring implementation utilizing the Free Large Integer Package (known more widely as lip) which was created by Arjen K. Lenstra (now a Professor Emeritus). This implementation includes Henri Cohen’s Trial Division algorithm, the Brent-Cohen-Pollard rho method, the Cohen-Pollard p – 1 stage 1 method, and the Lenstra lip Elliptic Curve Method. If I can get the proper authorization, I will later post the source code.
total time required for initialization: 0.056000 seconds
enter number below:
2^111+2
== Menu ==
1 Trial Division
2 Pollard-Brent-Cohen rho
3 p - 1 Pollard-Cohen
4 Lenstra's Elliptic Curve Method
5 Pollard-Lenstra rho
1
2596148429267413814265248164610050
number is composite
factors:
total time required factoring: 0.014000 seconds:
2
5 ^ 2
41
397
2113
enter number below:
0
total time required for initialization: 0.056000 seconds
enter number below:
2^111+2
== Menu ==
1 Trial Division
2 Pollard-Brent-Cohen rho
3 p - 1 Pollard-Cohen
4 Lenstra's Elliptic Curve Method
5 Pollard-Lenstra rho
2
2596148429267413814265248164610050
number is composite
factors:
total time required factoring: 1.531000 seconds:
2
5 ^ 2
41
397
2113
415878438361
3630105520141
enter number below:
0
total time required for initialization: 0.055000 seconds
enter number below:
2^111+2
== Menu ==
1 Trial Division
2 Pollard-Brent-Cohen rho
3 p - 1 Pollard-Cohen
4 Lenstra's Elliptic Curve Method
5 Pollard-Lenstra rho
3
2596148429267413814265248164610050
number is composite
factors:
total time required factoring: 0.066000 seconds:
2
5 ^ 2
41
838861
415878438361
3630105520141
enter number below:
0
total time required for initialization: 0.056000 seconds
enter number below:
2^111+2
== Menu ==
1 Trial Division
2 Pollard-Brent-Cohen rho
3 p - 1 Pollard-Cohen
4 Lenstra's Elliptic Curve Method
5 Pollard-Lenstra rho
4
2596148429267413814265248164610050
number is composite
factors:
total time required factoring: 0.013000 seconds:
2
5
205
838861
415878438361
3630105520141
enter number below:
0
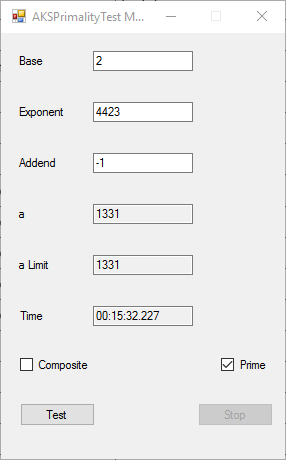
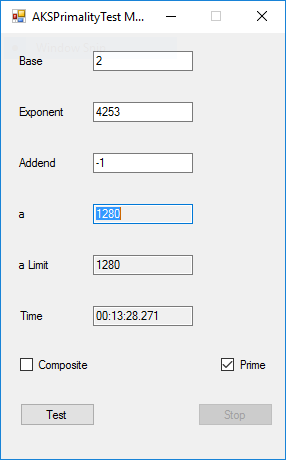
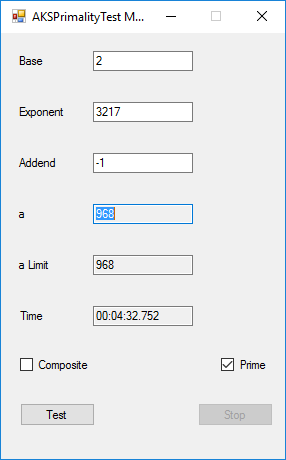
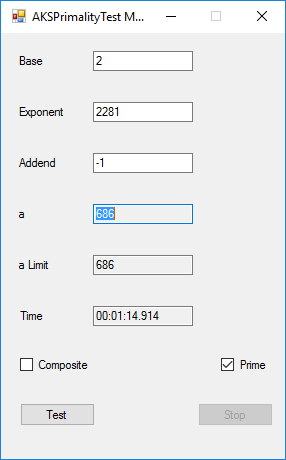
BigInteger Multitasking Agrawal, Kayal, and Saxena (AKS) Primality Test (c) June 19, 2016, by James Pate Williams, Jr. Microsoft TechNet Project Description
This application implements the algorithm described in the paper at the URL http://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf. I replaced Step 1 of the algorithm with the Miller-Rabin probabilistic primality test. If that test shows that the number is composite, I return the value COMPOSITE. This algorithm is much easier to implement and understand that Wieb Bosmer’s Primality Proving with Cyclotomy also known as the Jacobi sums primality test. As a test we determine that the following Mersenne numbers are prime: M_1279, M_2203, M_2281, M_3217, and M_4253 where M_n = 2 ^ n – 1, and the primes have 386, 664, 687, 969, and 1281 decimal digits, respectively. M_1279 was first proven prime by Raphael M. Robinson on June 25, 1952, using the Lucas-Lehmer test on a SWAC computer. The same author found that M_2203 was prime on October 7, 1952, and M_2281 was prime on October 9, 1952, using the same method and computer. Hans Riesel determined that M_3217 was prime on September 8, 1957, using the Lucas-Lehmer test on a BESK computer. M_4253 was proven prime on November 3, 1961 by Alexander Hurwitz using the Lucas-Lehmer test on an IBM 7090 mainframe computer. See http://www.mersenne.org/primes/ for many more Mersenne primes. All of the computations illustrated below were performed on a late November 2015 Dell XPS 8900 computer with 16 GB RAM Intel(R) Core(TM) i7-6700K CPU @ 4.00 GHz running Windows 10 Pro. The .Net framework is .Net 4.5.2. This is a multitasking version of the original BigInteger variant of the application. Someone with a quad core CPU with 8 virtual processors can try NumberTasks = 8 to see if that speeds up this application more or less. I usually try to limit the number of tasks to actual number of cores.