Category: C++ Computer Applications
Blog Entry © Wednesday, November 6, 2024, by James Pate Williams, Jr. Particle in a Finite Spherical Three-Dimensional Potential Well
The Bessel functions are from A Numerical Library in C for Scientists and Engineers (c) 1995 by H. T. Lau, PhD.
Blog Entry (c) Wednesday, November 6, 2024, by James Pate Williams, Jr. Small Angular Momentum Quantum Numbers Gaunt Coefficients
// GauntCoefficients.cpp (c) Monday, November 4, 2024
// by James Pate Williams, Jr., BA, BS, MSWE, PhD
// Computes the Gaunt angular momentum coefficients
// Also the Wigner-3j symbols are calculated
// https://en.wikipedia.org/wiki/3-j_symbol
// https://doc.sagemath.org/html/en/reference/functions/sage/functions/wigner.html#
// https://www.geeksforgeeks.org/factorial-large-number/
#include <iostream>
using namespace std;
typedef long double real;
real pi;
// iterative n-factorial function
real Factorial(int n)
{
real factorial = 1;
for (int i = 2; i <= n; i++)
factorial *= i;
if (n < 0)
factorial = 0;
return factorial;
}
real Delta(int lt, int rt)
{
return lt == rt ? 1.0 : 0.0;
}
real Wigner3j(
int j1, int j2, int j3,
int m1, int m2, int m3)
{
real delta = Delta(m1 + m2 + m3, 0) *
powl(-1.0, j1 - j2 - m3);
real fact1 = Factorial(j1 + j2 - j3);
real fact2 = Factorial(j1 - j2 + j3);
real fact3 = Factorial(-j1 + j2 + j3);
real denom = Factorial(j1 + j2 + j3 + 1);
real numer = delta * sqrt(
fact1 * fact2 * fact3 / denom);
real fact4 = Factorial(j1 - m1);
real fact5 = Factorial(j1 + m1);
real fact6 = Factorial(j2 - m2);
real fact7 = Factorial(j2 + m2);
real fact8 = Factorial(j3 - m3);
real fact9 = Factorial(j3 + m3);
real sqrt1 = sqrtl(
fact4 * fact5 * fact6 * fact7 * fact8 * fact9);
real sumK = 0;
int K = (int)fmaxl(0, fmaxl((real)j2 - j3 - m1,
(real)j1 - j3 + m2));
int N = (int)fminl((real)j1 + j2 - j3,
fminl((real)j1 - m1, (real)j2 + m2));
for (int k = K; k <= N; k++)
{
real f0 = Factorial(k);
real f1 = Factorial(j1 + j2 - j3 - k);
real f2 = Factorial(j1 - m1 - k);
real f3 = Factorial(j2 + m2 - k);
real f4 = Factorial(j3 - j2 + m1 + k);
real f5 = Factorial(j3 - j1 - m2 + k);
sumK += powl(-1.0, k) / (f0 * f1 * f2 * f3 * f4 * f5);
}
return numer * sqrt1 * sumK;
}
real GauntCoefficient(
int l1, int l2, int l3, int m1, int m2, int m3)
{
real factor = sqrtl(
(2.0 * l1 + 1.0) *
(2.0 * l2 + 1.0) *
(2.0 * l3 + 1.0) /
(4.0 * pi));
real wigner1 = Wigner3j(l1, l2, l3, 0, 0, 0);
real wigner2 = Wigner3j(l1, l2, l3, m1, m2, m3);
return factor * wigner1 * wigner2;
}
int main()
{
pi = 4.0 * atanl(1.0);
cout << "Gaunt(1, 0, 1, 1, 0, 0) = ";
cout << GauntCoefficient(1, 0, 1, 1, 0, 0);
cout << endl;
cout << "Gaunt(1, 0, 1, 1, 0, -1) = ";
cout << GauntCoefficient(1, 0, 1, 1, 0, -1);
cout << endl;
real number = -1.0 / 2.0 / sqrtl(pi);
cout << "-1.0 / 2.0 / sqrt(pi) = ";
cout << number << endl;
return 0;
}
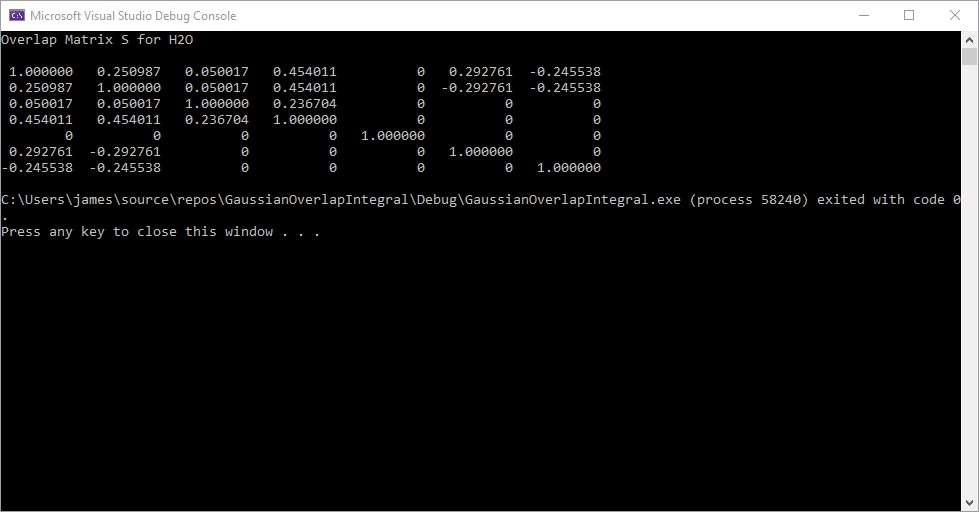
Blog Entry © Friday, November 1, 2024, by James Pate Williams, Jr. Calculation of the Overlap Matrix for the Water Molecule (H2O) Using a Contracted Set of Gaussian Orbitals
Reference: https://content.wolfram.com/sites/19/2012/02/Ho.pdf
I reproduced most of the computations in the MATHMATICA reference. The water molecule is a planar molecule that lies in the YZ-plane.
Blog Entry © Tuesday, October 29, 2024, by James Pate Williams, Jr. Second Order Quantum Mechanical Perturbation Calculation Part II
Blog Entry © Tuesday, October 29, 2024, by James Pate Williams, Jr. Second Order Quantum Mechanical Perturbation Calculation Part I
Blog Entry (c) Monday, October 28, 2024, by James Pate Williams, Jr. Two Methods of Computing the Gaussian Type Orbital 1s Integrals (Corrected Version)
Blog Entry (c) Sunday, October 27, 2024, by James Pate Williams, Jr. Curve Fitting
Blog Entry (c) Saturday, October 26, 2024, by James Pate Williams, Jr. Interpolation by Polynomials and Cramer’s Rule Calculations of Matrix Determinants and Inverses
Blog Entry (c) Friday, October 25, 2024, by James Pate Williams, Jr. Optimization Methods
The optimization methods that were programmed are the Simplex Algorithm, the Steepest Descent method, and Newton’s Method. The Simplex Algorithm was given to me by Microsoft Copilot. The other two methods are from Elementary Numerical Analysis: An Algorithmic Approach 3rd Edition (c) 1980 by S.D. Conte and Carl de Boor.