Category: C++ Computer Applications
Blog Entry Thursday, July 25, 2024, (c) James Pate Williams, Jr. Newton’s Method for Finding the Real Roots of a Real Polynomial
degree (0 to quit) = 5
a[5] = 1
a[4] = -15.5
a[3] = 77.5
a[2] = -155
a[1] = 124
a[0] = -32
x[0] = 0.45
x[1] = 0.9
x[2] = 1.8
x[3] = 3.6
x[4] = 7.2
iterations = 31
root[0] = 5.0000000000e-01
root[1] = 1.0000000000e+00
root[2] = 2.0000000000e+00
root[3] = 4.0000000000e+00
root[4] = 8.0000000000e+00
func[0] = 0.0000000000e+00
func[1] = 0.0000000000e+00
func[2] = 0.0000000000e+00
func[3] = 0.0000000000e+00
func[4] = 0.0000000000e+00
degree (0 to quit) =
Blog Entry (c) Tuesday, July 23, 2024, by James Pate Williams, Jr. Mueller’s Method for Finding the Complex and/or Real Roots of a Complex and/or Real Polynomial
I originally implemented this algorithm in FORTRAN IV in the Summer Quarter of 1982 at the Georgia Institute of Technology. I was taking a course named “Scientific Computing I” taught by Professor Gunter Meyer. I made a B in the class. Later in 2015 I re-implemented the recipe in C# using Visual Studio 2008 Professional. VS 2015 did not have support for complex numbers nor large integers. In December of 2015 I upgraded to Visual Studio 2015 Professional which has support for big integers and complex numbers. I used Visual Studio 2019 Community version for this project. Root below should be function.
Degree (0 to quit) = 2
coefficient[2].real = 1
coefficient[2].imag = 0
coefficient[1].real = 1
coefficient[1].imag = 0
coefficient[0].real = 1
coefficient[0].imag = 0
zero[0].real = -5.0000000000e-01 zero[0].imag = 8.6602540378e-01
zero[1].real = -5.0000000000e-01 zero[1].imag = -8.6602540378e-01
root[0].real = 0.0000000000e+00 root[0].imag = -2.2204460493e-16
root[1].real = 3.3306690739e-16 root[1].imag = -7.7715611724e-16
Degree (0 to quit) = 3
coefficient[3].real = 1
coefficient[3].imag = 0
coefficient[2].real = 0
coefficient[2].imag = 0
coefficient[1].real = -18.1
coefficient[1].imag = 0
coefficient[0].real = -34.8
coefficient[0].imag = 0
zero[0].real = -2.5026325486e+00 zero[0].imag = -8.3036679880e-01
zero[1].real = -2.5026325486e+00 zero[1].imag = 8.3036679880e-01
zero[2].real = 5.0052650973e+00 zero[2].imag = 2.7417672687e-15
root[0].real = 0.0000000000e+00 root[0].imag = 1.7763568394e-15
root[1].real = 3.5527136788e-14 root[1].imag = -1.7763568394e-14
root[2].real = 2.8421709430e-14 root[2].imag = 1.5643985575e-13
Degree (0 to quit) = 5
coefficient[5].real = 1
coefficient[5].imag = 0
coefficient[4].real = 2
coefficient[4].imag = 0
coefficient[3].real = 3
coefficient[3].imag = 0
coefficient[2].real = 4
coefficient[2].imag = 0
coefficient[1].real = 5
coefficient[1].imag = 0
coefficient[0].real = 6
coefficient[0].imag = 0
zero[0].real = -8.0578646939e-01 zero[0].imag = 1.2229047134e+00
zero[1].real = -8.0578646939e-01 zero[1].imag = -1.2229047134e+00
zero[2].real = 5.5168546346e-01 zero[2].imag = 1.2533488603e+00
zero[3].real = 5.5168546346e-01 zero[3].imag = -1.2533488603e+00
zero[4].real = -1.4917979881e+00 zero[4].imag = 1.8329656063e-15
root[0].real = 8.8817841970e-16 root[0].imag = 4.4408920985e-16
root[1].real = -2.6645352591e-15 root[1].imag = -4.4408920985e-16
root[2].real = 8.8817841970e-16 root[2].imag = 1.7763568394e-15
root[3].real = 3.4638958368e-14 root[3].imag = -1.4210854715e-14
root[4].real = 8.8817841970e-16 root[4].imag = 2.0710031449e-14
Blog Entry Sunday, July 21, 2024 (c) James Pate Williams, Jr. Another Easy Internet Mathematics Problem
x = 1.2679491924e+00 y = 4.7320508076e+00
f = 0.0000000000e+00 g = 0.0000000000e+00
iterations = 100
legend: f = x + y – 6, g = x * y – 6
The solution was found via my Win32 C application whose source code is presented below (the method is the Newton iteration for systems of linear and/or non-linear equations):
Blog Entry Friday, July 19, 2024, Easy Internet Math “Puzzle” (c) James Pate Williams, Jr.
#include <math.h>
#include <iostream>
using namespace std;
long double f(long double x)
{
return powl(8.0, x) - powl(2.0, x) -
2.0 * (powl(6.0, x) - powl(3.0, x));
}
long double g(long double x)
{
return powl(8.0, x) * logl(8.0) - powl(2.0, x) * logl(2.0) -
2.0 * (powl(6.0, x) * logl(6.0) - powl(3.0, x) * logl(3.0));
}
long double Newton(long double x, int maxIts, int& iterations)
{
long double x0 = x;
long double x1 = 0.0;
iterations = 0;
while (true) {
long double dx = 0.0;
long double fx = f(x0);
long double gx = g(x0);
x1 = x0 - fx / gx;
dx = fabsl(x1 - x0);
iterations++;
if (dx < 1.0e-15)
break;
if (fabsl(fx) < 1.0e-15)
break;
if (iterations == maxIts)
break;
x0 = x1;
}
return x1;
}
int main() {
int iterations = 0, maxIts;
long double x0 = 0.0, x1 = 0.0;
while (true) {
cout << "x0 = ";
cin >> x0;
if (x0 == 0)
break;
cout << "maximum iterations = ";
cin >> maxIts;
x1 = Newton(x0, maxIts, iterations);
cout << "x1 = " << x1 << endl;
cout << "iterations = ";
cout << iterations << endl;
}
return 0;
}
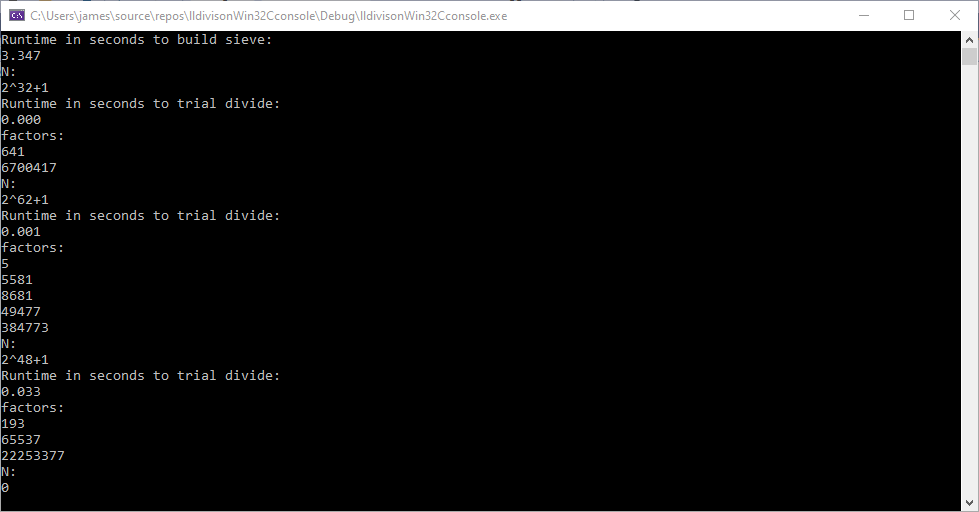
Blog Entry Monday, July 8, 2024, (c) James Pate Williams, Jr. Relatively Fast 64-bit Trial Division Using Henri Cohen’s Algorithm
The sieve of Eratosthenes handles primes up to an upper bound of 100,000,000. The number of primes is 5,761,455. Below are a few examples runs of the app. I have also created C source code for trial division and other factoring algorithms that use Professor Emeritus Arjen K. Lenstra’s Free Large Integer Package also known as lip.

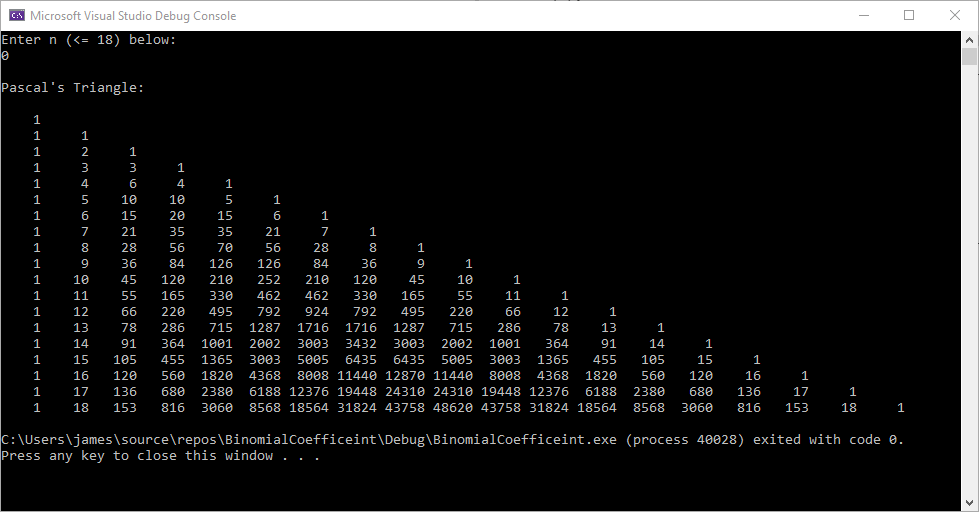
Blog Entry Monday, June 24, 2024 (c) James Pate Williams, Jr. Computing Binomial Coefficients and Pascal’s Triangle in the C Language
Enter n (<= 18) below:
5
Enter k (<= 18) below:
0
1 1
Enter n (<= 18) below:
5
Enter k (<= 18) below:
1
5 5
Enter n (<= 18) below:
5
Enter k (<= 18) below:
2
10 10
Enter n (<= 18) below:
0
Enter n (<= 18) below:
0
Pascal's Triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
1 17 136 680 2380 6188 12376 19448 24310 24310 19448 12376 6188 2380 680 136 17 1
1 18 153 816 3060 8568 18564 31824 43758 48620 43758 31824 18564 8568 3060 816 153 18 1
C:\Users\james\source\repos\BinomialCoefficeint\Debug\BinomialCoefficeint.exe (process 40028) exited with code 0.
Press any key to close this window . . .
// BinomialCoefficient.c (c) Monday, June 24, 2024
// by James Pate Williams, Jr. BA, BS, MSwE, PhD
#include <stdio.h>
#include <stdlib.h>
typedef long long ll;
ll** Binomial(ll n)
{
ll** C = (ll**)calloc(n + 1, sizeof(ll*));
if (C == NULL)
exit(-1);
for (int i = 0; i < n + 1; i++)
{
C[i] = (ll*)calloc(n + 1, sizeof(ll));
if (C[i] == NULL)
exit(-1);
}
if (n >= 0)
{
C[0][0] = 1;
}
if (n >= 1)
{
C[1][0] = 1;
C[1][1] = 1;
}
if (n >= 2)
{
for (int i = 2; i <= n; i++)
{
for (int j = 2; j <= n; j++)
{
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
return C;
}
ll Factorial(ll n)
{
ll fact = 1;
if (n > 1)
{
for (int i = 2; i <= n; i++)
fact = i * fact;
}
return fact;
}
ll BC(ll n, ll k)
{
return Factorial(n) / (Factorial(n - k) * Factorial(k));
}
int main()
{
int i = 0, j = 0;
ll** C = Binomial(20);
while (1)
{
char buffer[256] = { '\0' };
printf_s("Enter n (<= 18) below:\n");
scanf_s("%s", buffer, sizeof(buffer));
printf_s("\n");
ll n = atoll(buffer);
if (n == 0)
break;
printf_s("Enter k (<= 18) below:\n");
scanf_s("%s", buffer, sizeof(buffer));
printf_s("\n");
ll k = atoll(buffer);
printf_s("%lld\t%lld\n\n", C[n + 2][k + 2], BC(n, k));
}
printf_s("Pascal's Triangle:\n\n");
for (i = 2; i <= 20; i++)
{
for (j = 2; j <= 20; j++)
if (C[i][j] != 0)
printf_s("%5lld ", C[i][j]);
printf_s("\n");
}
for (i = 0; i <= 20; i++)
free(C[i]);
free(C);
}
Another Blog Entry for Thursday, June 20, 2024 (c) James Pate Williams, Jr. Atkin Primality Certificates
Blog Entry Thursday, June 20, 2024 (c) James Pate Williams, Jr. Some 3D Graphs (Application Edited 2024)
Blog Entry Tuesday, June 18, 2024 (c) James Pate Williams, Jr. FreeLIP Computation of Euler Numbers and Tangent Numbers
FreeLIP is a free large integer package solely created by Professor Emeritus Arjen K. Lenstra of the Number Field Sieve fame. He developed FreeLIP while he was an employee of AT&T – Lucent in the late 1980s. His copyright notice in the header file, lip.h, states copyright from 1989 to 1997. I have been using this excellent number theoretical package since the late 1990s. See the paper by Donald E. Knuth and Thomas J. Buckholtz for the formula for Tangent Numbers. I can’t remember where I got the Euler Numbers recurrence relation. I wrote a C# application in 2015 for computing Euler Numbers. The code below is in the vanilla C computer language. Excellent resources for the Euler and tangent numbers also known as zag numbers are: