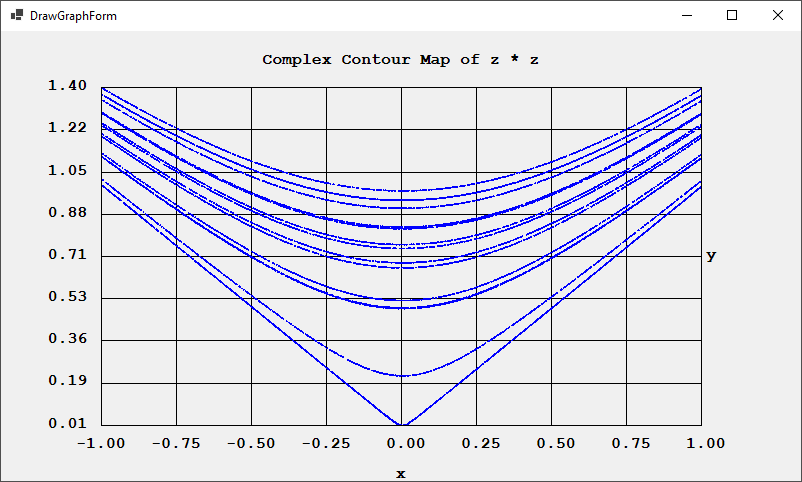
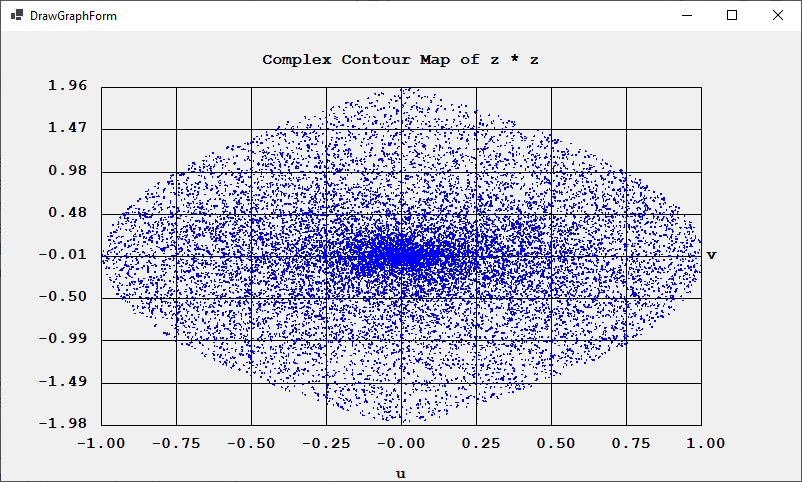
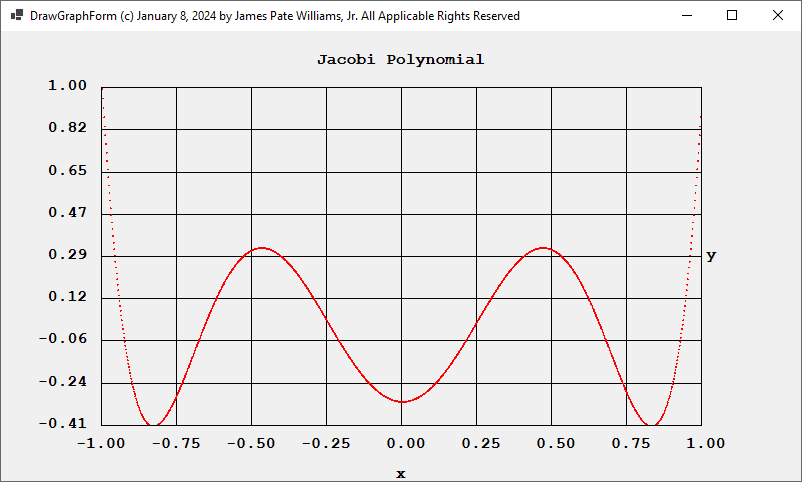
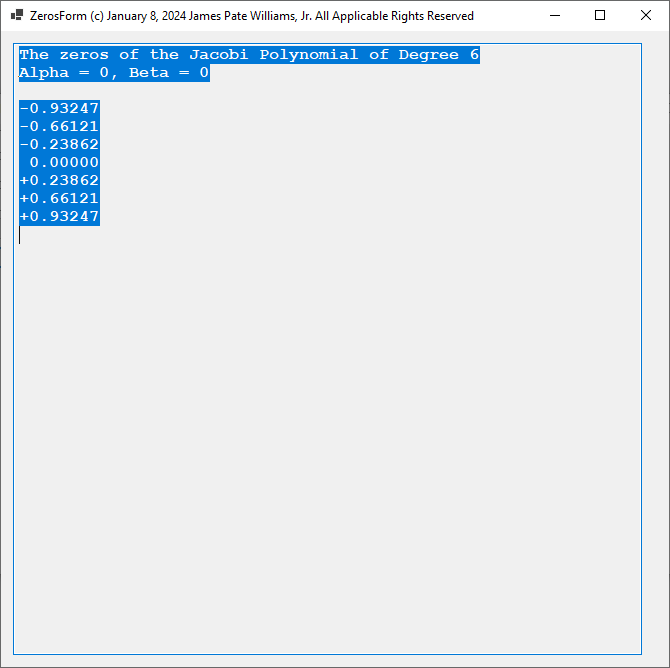
Back in 2015 I translated a multiple integration FORTRAN subroutine to C# using switch statements to emulate conditional and unconditional go to statements. On January 15 – January 16, 2024, I translated my C# source code to vanilla C. Below is the FORTRAN subroutine’s website:
Remarks on algorithm 006: An adaptive algorithm for numerical integration over an N-dimensional rectangular region – ScienceDirect
Here are some web pages with examples of triple integration:
3.4: Numerical Approximation of Multiple Integrals – Mathematics LibreTexts
3.3: Triple Integrals – Mathematics LibreTexts
https://tutorial.math.lamar.edu/Classes/CalcIII/IteratedIntegrals.aspx
https://tutorial.math.lamar.edu/Solutions/CalcIII/TripleIntegrals/Prob1.aspx
https://tutorial.math.lamar.edu/Problems/CalcIII/TripleIntegrals.aspx
I created a C test application to attempt to verify some of the results in online sources. For one example I also used my C# program.
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option: 1
f(x, y, z) = 8 * x * y * z
[0.000000, 1.000000] x [1.000000, 2.000000] x [2.000000, 3.000000]
N Integral -+Error % Error
10 0.754706 0.250631 94.968627
100 1.050263 0.126084 92.998246
1000 1.032125 0.036751 93.119165
10000 1.015068 0.011748 93.232880
100000 1.004080 0.003706 93.306131
1000000 1.000650 0.001169 93.329000
nQuadrature Integral Value and Percent Error: 15.000000 0.000000
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option:
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option: 2
f(x, y, z) = 4 * x * x * y - z * z * z
[2.000000, 3.000000] x [-1.000000, 4.000000] x [1.000000, 0.000000]
N Integral -+Error % Error
10 -12.087502 -3.929801 93.596026
100 -17.622371 -1.969516 90.663644
1000 -17.963837 -0.612528 90.482735
10000 -18.129559 -0.197880 90.394936
100000 -18.018231 -0.062690 90.453917
1000000 -17.939045 -0.019779 90.495870
nQuadrature Integral Value and Percent Error: 188.750000 200.000000
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option:
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option: 3
f(x, y, z) = x * y + z
[0.000000, 3.000000] x [0.000000, 2.000000] x [0.000000, 1.000000]
N Integral -+Error % Error
10 9.243858 2.121562 22.967849
100 12.062489 0.808150 0.520745
1000 12.096541 0.255335 0.804509
10000 12.094473 0.081030 0.787275
100000 12.051033 0.025704 0.425271
1000000 12.009588 0.008121 0.079900
nQuadrature Integral Value and Percent Error: 12.000000 0.000000
== Menu ==
1 f(x, y, z) = 8 * x * y * z
2 f(x, y, z) = 4 * x * x * y - z * z * z
3 f(x, y, z) = x * y + z
5 Exit
Option:
desired relative error 0.001
f# integral epsilon number err code
1 +1.4346639496E+000 1.295116E-003 257 0
2 +5.7531639665E-001 5.745470E-004 97 0
3 +2.1527578485E+000 1.793429E-003 45 0
4 +1.5998921741E+001 1.579802E-002 151 0
5 +1.8390615688E-001 6.510967E-005 97 0
6 -4.0003324629E+000 3.747971E-003 17 0
7 +8.6330831791E-001 8.563683E-004 45 0
8 +1.5000000000E+001 8.850520E-011 45 0
9 +1.8875000000E+002 1.109797E-009 45 0
10 +1.2000000000E+001 7.081136E-011 45 0
f# abs errror percent error
1 +9.7938837210E-005 +6.8261387483E-003
2 +4.7748257754E-005 +8.2987892410E-003
3 +6.1501589893E-004 +2.8576909005E-002
4 +1.0782593204E-003 +6.7391207526E-003
5 +9.9602348685E-007 +5.4159040098E-004
6 +3.3246288154E-004 +8.3115720386E-003
7 +2.6210055455E-004 +3.0369237392E-002
8 +8.8506979523E-011 +5.9004653015E-010
9 +1.1098109098E-009 +5.8797928998E-010
10 +7.0812689046E-011 +5.9010574205E-010
Numbers 8-10 in the preceding data correspond to the three three-dimensional functions in the menu illustrated above. The website claims option 2 in the Menu integral is -755 / 4 = -188.75. My calculation is the same magnitude but a positive sign.