I wrote a C# program to graph NASA’s Earth Atmospheric Model’s variation of air density with height in Imperial Units and the United States Navy’s air density altitude equation.
Earth Atmosphere Model – Imperial Units (nasa.gov)
The USN’s formula for density – altitude is found in “Exterior ballistics, 1935” by Lieutenant Commander Ernest Edward Herrmann who was an instructor at the United States Naval Academy.
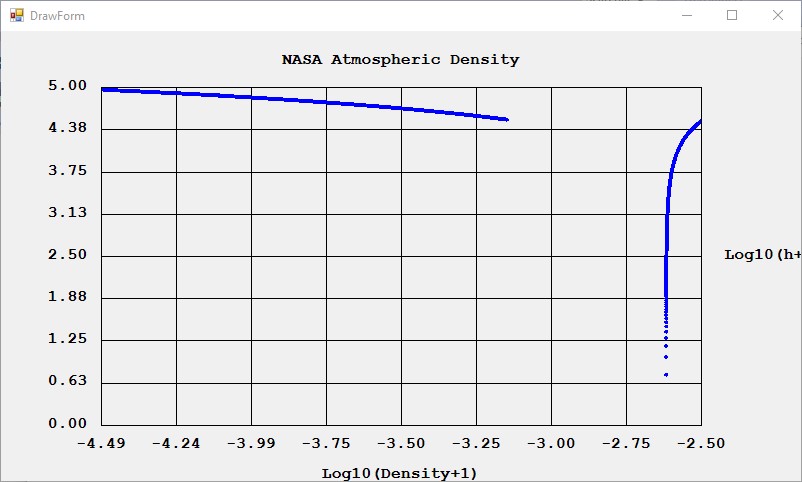
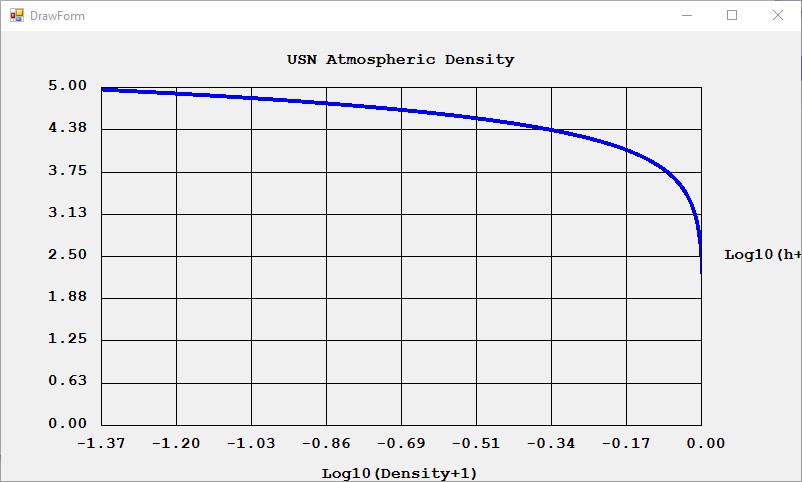
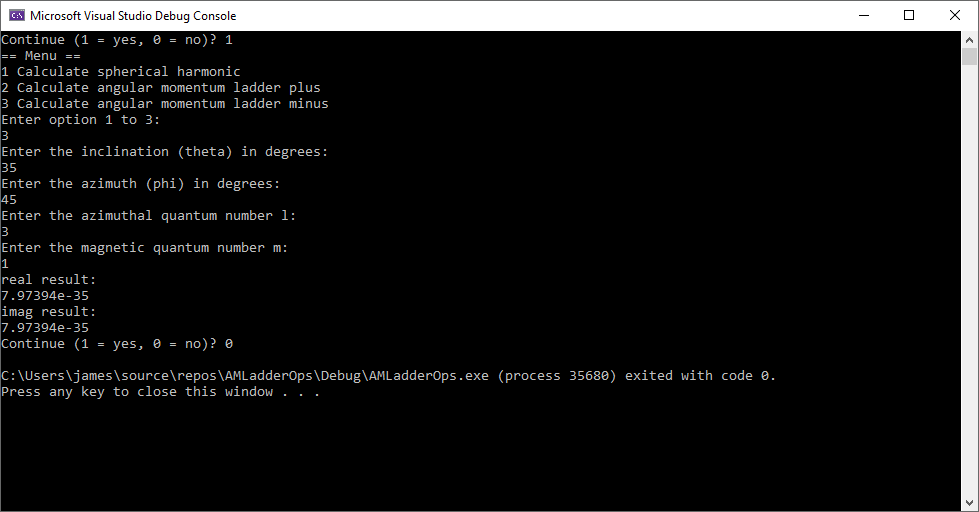
My father, James Pate Williams, Sr. (Born November 8, 1912, and Died February 10, 1993) was forced to quit school at the age of thirteen in 1925 or 1926 and was initially a sweeper at the West-Point Textiles Company’s Dixie cotton mill on Greenville Street in LaGrange, Georgia. The reason he quit school was to support his birth family after they were abandoned by my Williams side grandfather. Sometime in the 1930s my father received a cost accountant degree from LaSalle Extension University based in Chicago, Illinois. He corresponded via mail with his professors to earn his degree. LaSalle Extension University was one of the first examples of a distance learning center. While on the job he used a Friden tabulating machine, a K&E drafting kit, and K&E slide rule. I probably got my love of mathematics and numbers from my birth parents. My father taught me how to use a compass, protractor, slide rule, and tabulating machine. He used paper spreadsheets and his Friden calculator to maintain household expenses and to document his and my mother’s income tax. My father was also in charge of the Civil Defense equipment stored at Dixie Mill. That Cold War era equipment included a Roentgen measuring device and Geiger counter. I learned how to use both Civil Defense devices while I was in high school.
The following graphs and data are for a hypothetical engagement between the Battleship Iowa (BB-61) and an unlucky enemy warship. My numbers are very close to those found in Ordnance Pamphlet 770 at the following website:
https://eugeneleeslover.com/USN-GUNS-AND-RANGE-TABLES/OP-770-1.html
Does the following thought experiment make sense?
Suppose we have a positively charged quantum mechanical particle in a finite potential energy well. Also suppose there is a free negatively charged quantum mechanical particle outside the potential energy well. There is a measurable probability that the positively charged particle will tunnel through the potential energy well and perhaps be attracted to the negatively charged particle. Likewise, the negatively charged particle has a finite probability of penetrating the potential energy well and hooking up with the positively charged particle should it still be trapped in the well. There is no “spooky action at a distance” to use Albert Einstein’s 1930s definition of quantum entanglement in this example since this electromagnetic attraction is a local phenomenon (?). The positively charged particle cannot exert an attractive force until it tunnels through the energy barrier or otherwise the negatively charged particle winds up breaking into the well. I don’t know exactly how quantum electrodynamics would explain this example. Perhaps the positively charged particle is a positron (antimatter lepton) and the negatively charged particle is a plain vanilla electron. We know that the local result of the interaction of our two matter-antimatter particles is an annihilation event whereby two energetic photons are created, or other products are generated.
https://en.wikipedia.org/wiki/Annihilation#/media/File:Electron_Positron_Annihilation.png
Numerical Explorations 
