Factoring with Cubic Integers – Numerical Explorations

Preliminary Factorization Results of the Thirteenth Fermat Number (c) February 5, 2024, by James Pate Williams, Jr.

I am working on a factorization of the Thirteenth Fermat number which is 2 ^ 8192 + 1 and is 2,467 decimal digits in length. I am using Pollard’s factoring with cubic integers on the number (2 ^ 2731) ^ 3 + 2. I am also utilizing a homegrown variant of the venerable Pollard and Brent rho method and Arjen K. Lenstra’s Free LIP Elliptic Curve Method. I can factor the seventh Fermat number 2 ^ 128 + 1 in five to thirty minutes using my C# code. The factoring with cubic integers code is in C and uses Free-LIP.

Fermat factoring status (prothsearch.com)

The following is a run of Lenstra’s ECM algorithm:

== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^8192+1
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 1

2710954639361 p # digits 13
3603109844542291969 p # digits 19
Runtime (s) = 17015.344000

I aborted the previous computation due to the fact I was curious about the number of prime factors that could be found on personal computer. I will try a lot more calculation time in a future run. My homegrown application is able to at least find the first factor of Fermat Number 13.

Factorizations of Some Fibonacci Sequence Numbers, Lucas Sequence Numbers and Some Other Numbers Using Arjen K. Lenstra’s Free Large Integer Package and the Elliptic Curve Method (c) January 28, 2024, by James Pate Williams, Jr.

All of the following computations were performed on a late 2015 Dell XPS 8900 personal computer with a 64-bit Intel Core I7 processor @ 4.0GHz with 16GB of DDR2 RAM.

Factorization of Six Fibonacci Sequence Numbers:

 

Fibonacci 500

# digits 105

5 ^ 2 p # digits 1

15 c # digits 2

101 p # digits 3

401 p # digits 3

1661 c # digits 4

3001 p # digits 4

10291 c # digits 5

570601 p # digits 6

112128001 p # digits 9

1353439001 p # digits 10

28143378001 p # digits 11

5465167948001 p # digits 13

84817574770589638001 p # digits 20

158414167964045700001 p # digits 21

Runtime (s) = 1.206000



Fibonacci 505

# digits 106

5 p # digits 1

743519377 p # digits 9

44614641121 p # digits 11

770857978613 p # digits 12

960700389041 p # digits 12

12588421794766514566269164716286291055826556238643852856601641 p # digits 62

Runtime (s) = 1.959000



Fibonacci 510

# digits 107

2 ^ 3 p # digits 1

11 p # digits 2

61 p # digits 2

1021 p # digits 4

1597 p # digits 4

3469 p # digits 4

3571 p # digits 4

9521 p # digits 4

53551 p # digits 5

95881 p # digits 5

142445 c # digits 6

1158551 p # digits 7

3415914041 p # digits 10

20778644396941 p # digits 14

20862774425341 p # digits 14

81358225616651 c # digits 14

162716451241291 p # digits 15

Runtime (s) = 2.682000



Fibonacci 515

# digits 108

5 p # digits 1

519121 p # digits 6

5644193 p # digits 7

512119709 p # digits 9

84388938382141 p # digits 14

300367026458796424297447559250634818495937628065437243817852436228914621 p # digits 72

Runtime (s) = 7.861000



Fibonacci 520

# digits 109

131 p # digits 3

451 c # digits 3

521 p # digits 3

2081 p # digits 4

2161 p # digits 4

3121 p # digits 4

24571 p # digits 5

90481 p # digits 5

2519895 c # digits 7

21183761 p # digits 8

57089761 p # digits 8

102193207 p # digits 9

1932300241 p # digits 10

14736206161 p # digits 11

5836312049326721 p # digits 16

42426476041450801 p # digits 17

Runtime (s) = 5.155000



Fibonacci 525

# digits 110

2 p # digits 1

5 p # digits 1

421 p # digits 3

701 p # digits 3

3001 p # digits 4

3965 c # digits 4

4201 p # digits 4

141961 p # digits 6

2553601 p # digits 7

230686501 p # digits 9

8288823481 p # digits 10

82061511001 p # digits 11

19072991752501 c # digits 14

8481116649425701 p # digits 16

17231203730201189308301 p # digits 23

Runtime (s) = 2.026000

Factorization of Six Lucas Sequence Numbers



Lucas 340

113709744839525149336680459091826532688903186653162057995534262332121127

# digits 72

7 p # digits 1

2161 p # digits 4

5441 p # digits 4

897601 p # digits 6

23230657239121 p # digits 14

17276792316211992881 p # digits 20

3834936832404134644974961 p # digits 25

Runtime (s) = 109.103000



Lucas 345

# digits 73

2 ^ 2 p # digits 1

31 p # digits 2

461 p # digits 3

1151 p # digits 4

1529 c # digits 4

324301 p # digits 6

686551 p # digits 6

1485571 p # digits 7

4641631 p # digits 7

19965899801 c # digits 11

117169733521 p # digits 12

3490125311294161 p # digits 16

Runtime (s) = 0.032000



Lucas 350

13985374084677485786380981408251904922622980674054858121032362563653278123

# digits 74

3 p # digits 1

401 p # digits 3

2801 p # digits 4

11521 c # digits 5

28001 p # digits 5

570601 p # digits 6

12317523121 p # digits 11

248773766357061401 p # digits 18

7358192362316341243805801 p # digits 25

Runtime (s) = 21.047000



Lucas 355

69362907070206748494476200566565775354902428015845969798000696945226974645

# digits 74

5 p # digits 1

4261 p # digits 4

6673 p # digits 4

75309701 p # digits 8

309273161 p # digits 9

46165371073 p # digits 11

9207609261398081 p # digits 16

49279722643391864192801 p # digits 23

Runtime (s) = 40.726000



Lucas 360

769246427201094785080787978422393713094534885688979999504447628313150135520

# digits 75

2 ^ 5 p # digits 1

3 ^ 2 p # digits 1

23 p # digits 2

41 p # digits 2

105 c # digits 3

107 p # digits 3

241 p # digits 3

2161 p # digits 4

2521 p # digits 4

3439 c # digits 4

8641 p # digits 4

20641 p # digits 5

103681 p # digits 6

109441 p # digits 6

191306797 c # digits 9

10783342081 p # digits 11

13373763765986881 p # digits 17

Runtime (s) = 0.032000



Lucas 365

19076060504701386559675231910437330047906343529583769121365013189782992678011

# digits 77

11 p # digits 2

151549 p # digits 6

514651 p # digits 6

7015301 p # digits 7

8942501 p # digits 7

9157663121 p # digits 10

11899937029 p # digits 11

3252336525249736694804553589211 p # digits 31

The following two numbers were first factorized by J. M. Pollard on an 8-bit Phillips P2012 personal computer with 64 KB RAM and two 640 KB disc drives. The times required by Pollard were 41 and 47 hours.

2^144-3
22300745198530623141535718272648361505980413

# digits 44

492729991333 p # digits 12

45259565260477899162010980272761 p # digits 32

Runtime (s) = 0.086000

2^153+3
11417981541647679048466287755595961091061972995

# digits 47

5 p # digits 1

11 p # digits 2

600696432006490087537 p # digits 21

345598297796034189382757 p # digits 24

Runtime (s) = 0.676000

Partial factorization of the Twelfth Fermat Number 2^4096+1
# digits 1234

114689 p # digits 6

26017793 p # digits 8

63766529 p # digits 8

190274191361 p # digits 12

Runtime (s) = 1532.878000

Latest Software Development Project Started on Saturday, ‎October ‎15, ‎2022, ‏‎12:07:19 AM by James Pate Williams, Jr.

I am in the progress of translating (porting) my J. M. Pollard’s algorithm “Factoring with Cubic Integers” C# application to a Free LIP based vanilla C Windows 32-bit console application. The first phase of the method is to generate two factor bases namely a rational prime factor base and an algebraic integer prime factor base. I have included some preliminary results from this fast-moving computer programming task. I generated 2012 algebraic integer primes in about a minute and thirty seconds.

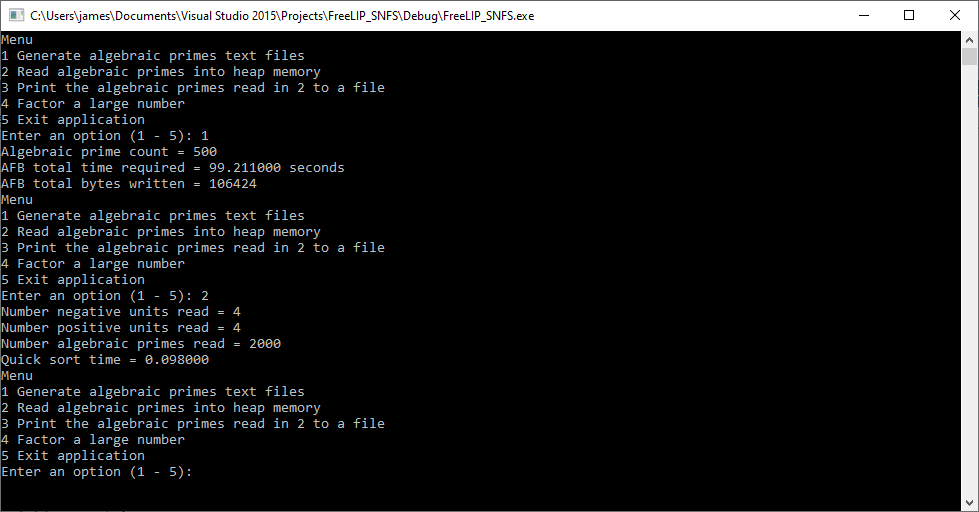
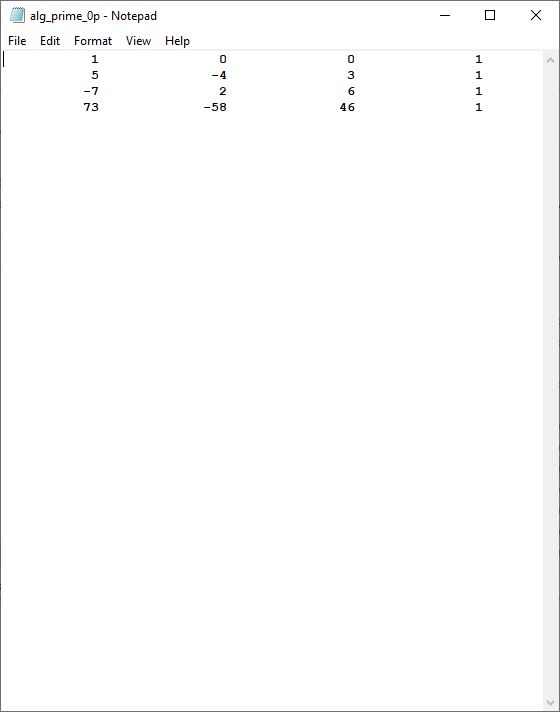
Generation of the Algebraic Integer Primes

Pollard Cubic Integer Factoring and Classical Shor Factoring Algorithms by James Pate Williams, Jr.

Back on Thursday, January 10, 2019, at 02:40 AM I started implementing J. M. Pollard’s factoring with cubic integers method and a classical variant of Shor’s quantum computer factoring algorithm. I have probably implemented at least three versions of Pollard’s magnificent work which led to the special number field sieve fast factoring method. I am working on translating my C# code of these two algorithms to Arjen K. Lenstra’s Free Large Integer Package in the C computer programming language. Appended to this electronic missive are factorizations of two small 19-decimal digit numbers 2^63-1 and 2^63+1. Pollard’s method requires that the exponent be divisible by three. Thus, we write the numbers as 2^ (21 * 3) plus or minus 1. You can factor numbers with different bases and small addends and subtrahends as long as the exponent is zero modulo 3. You will notice that Shor’s algorithm is very fast on these small numbers.

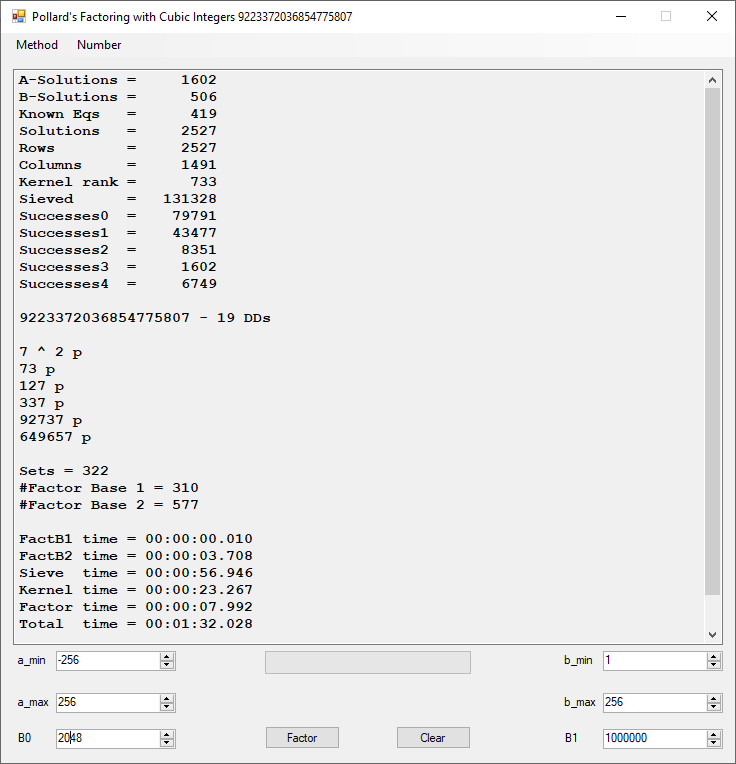
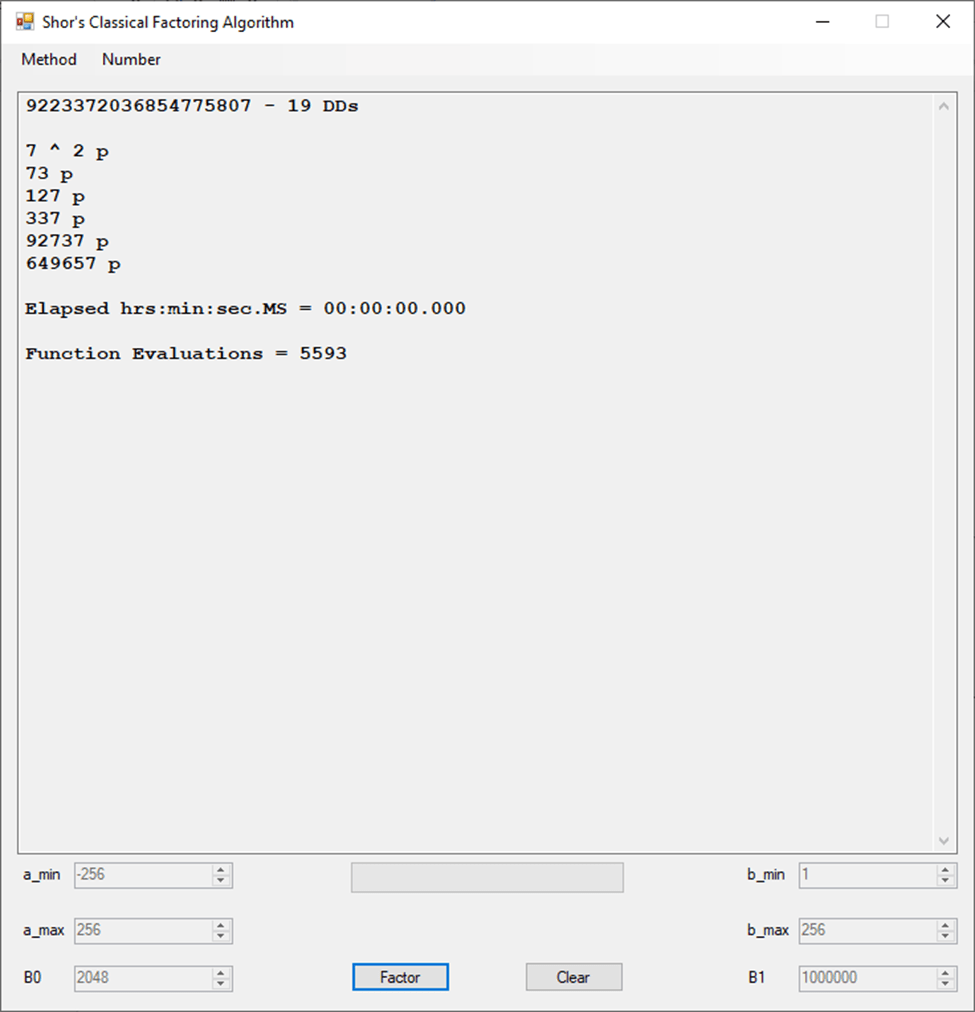
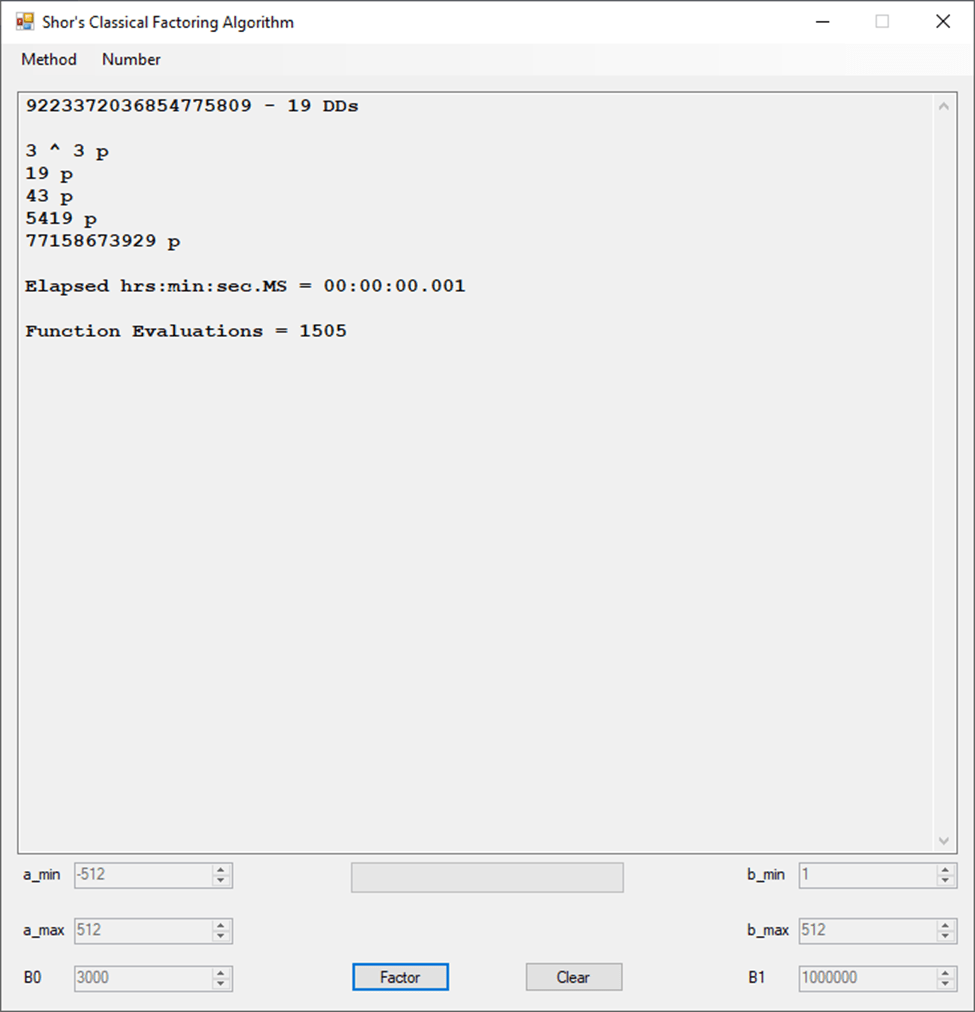
Pollard’s Factoring with Cubic Integers 2^63-1

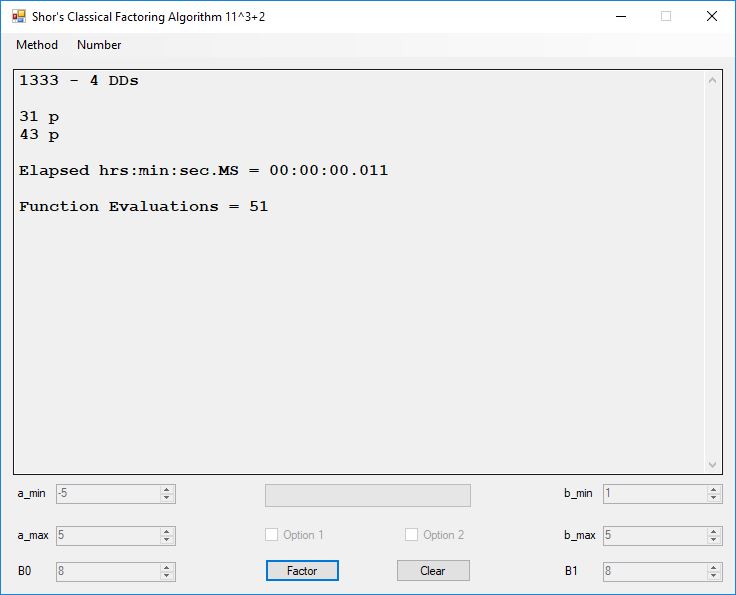
Classical Shor’s Algorithm Versus J. M. Pollard’s Factoring with Cubic Integers

We tried to factor the following numbers with each algorithm: 11^3+2, 2^33+2, 5^15+2, 2^66+2, 2^72+2, 2^81+2, 2^101+2, 2^129+2, and 2^183+2. Shor’s algorithm fully factored all of the numbers. Factoring with cubic integers fully factored all numbers except 2^66+2, 2^71+2, 2^129+2, and 2^183+2.

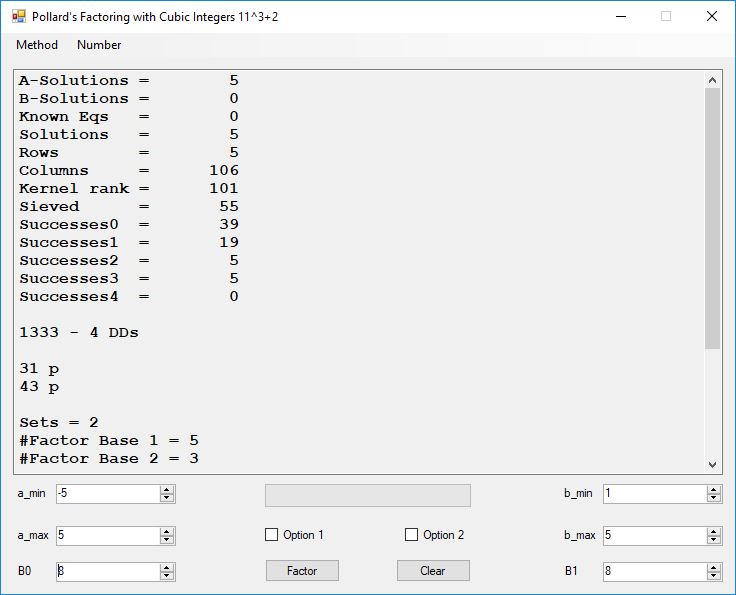
cs1cubic cs1shor

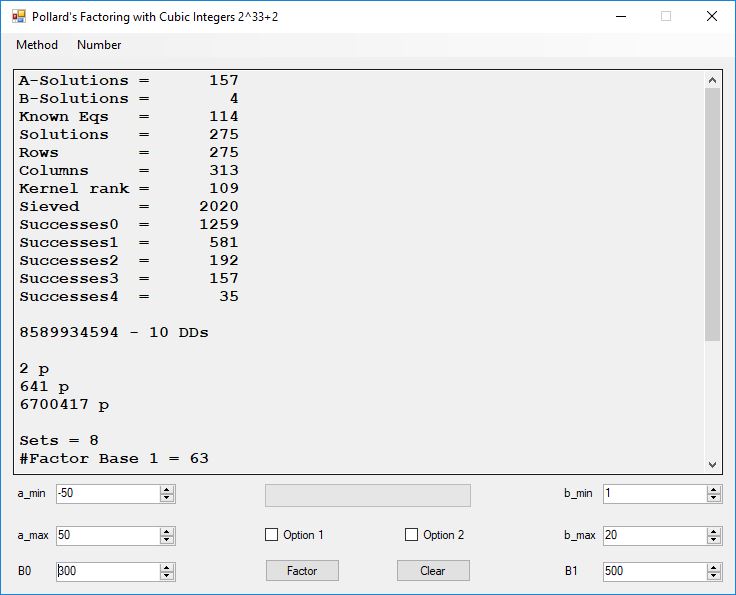
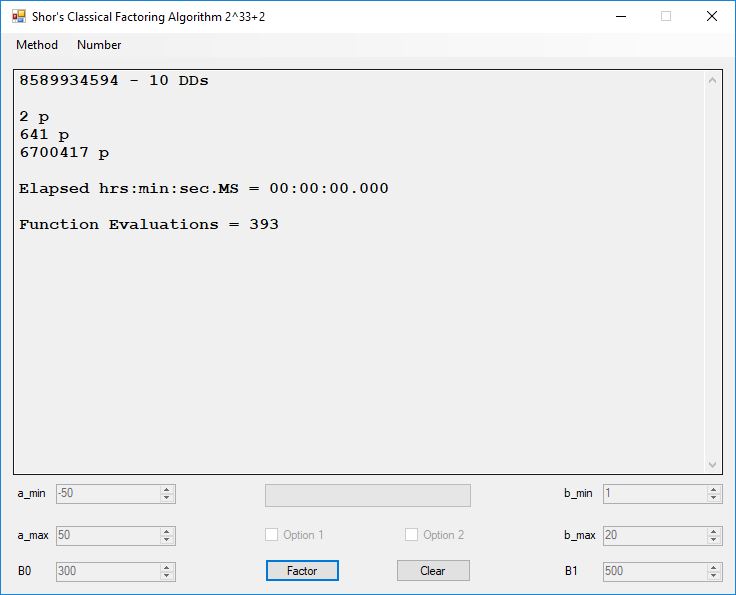
cs2cubic cs2shor

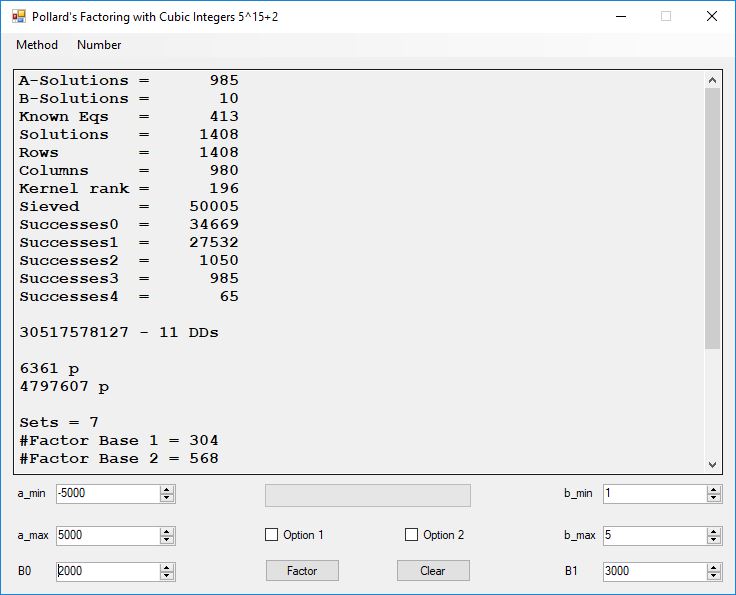
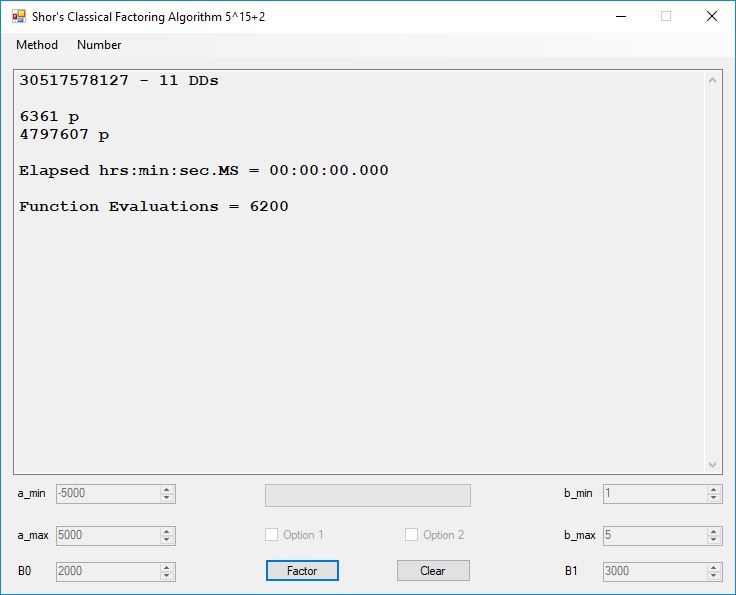
cs3cubic cs3shor

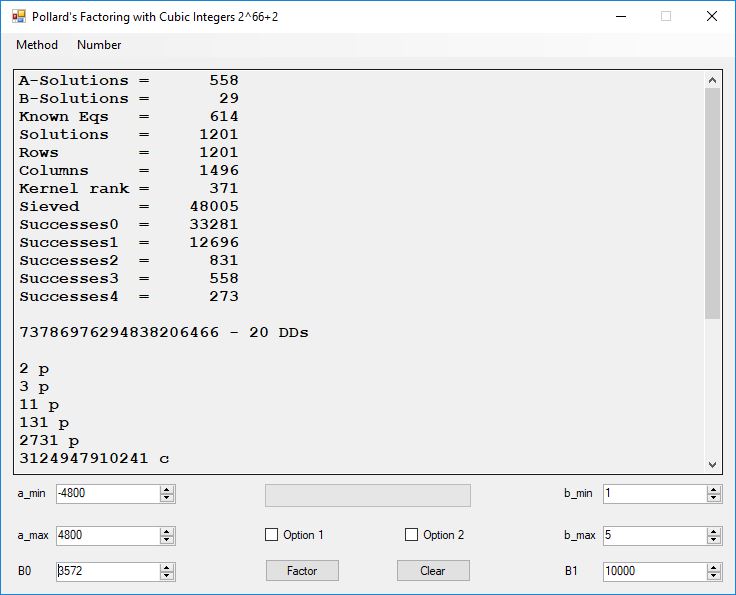
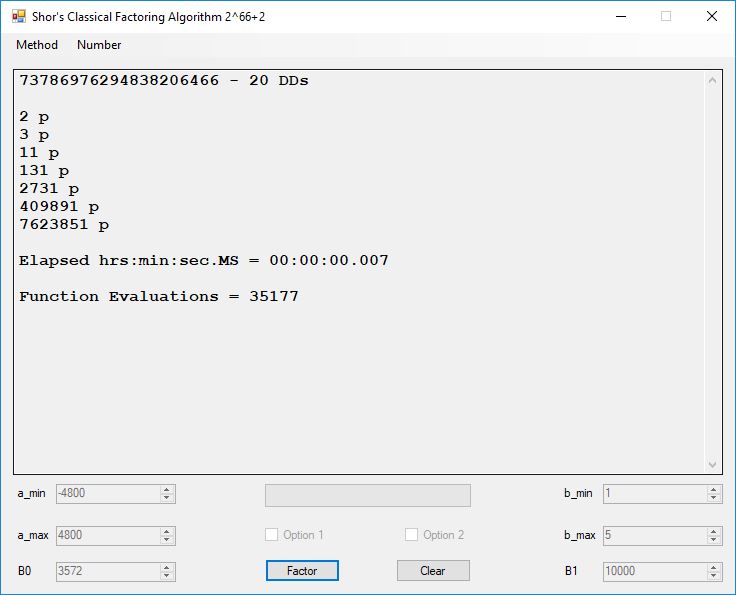
cs4cubic cs4shor

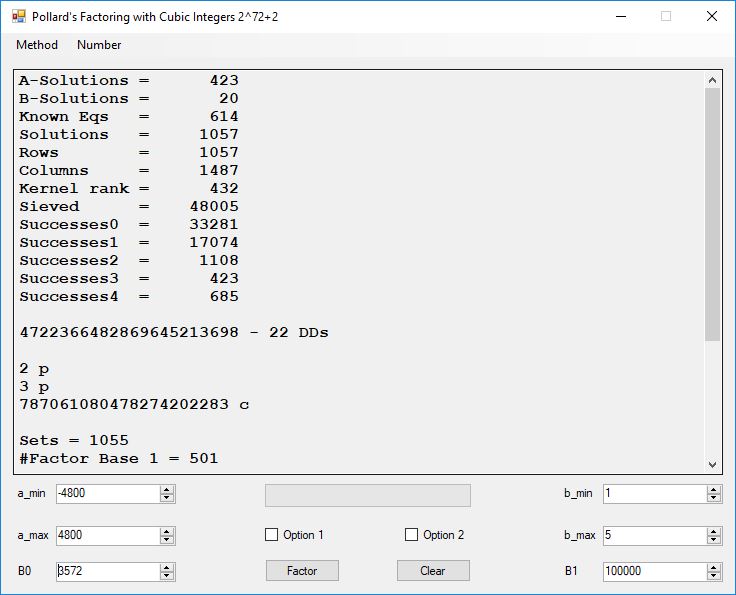
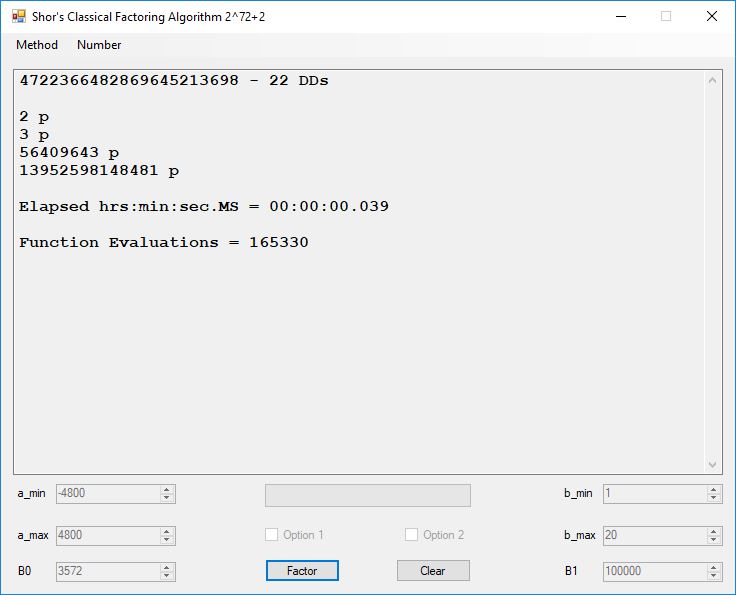
cs5cubic cs5shor

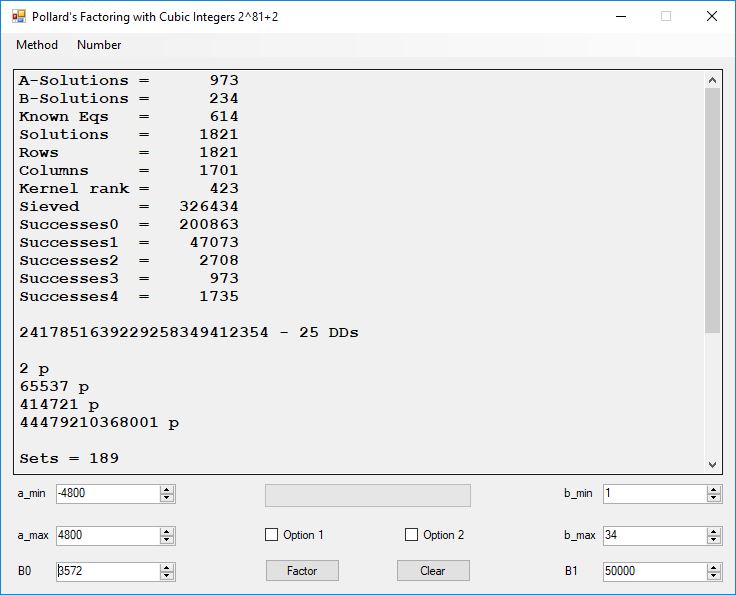
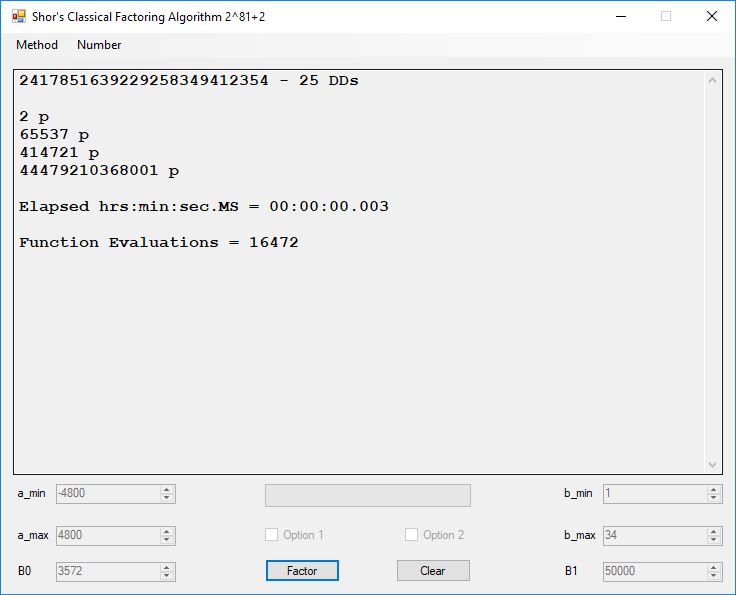
cs6cubic cs6shor

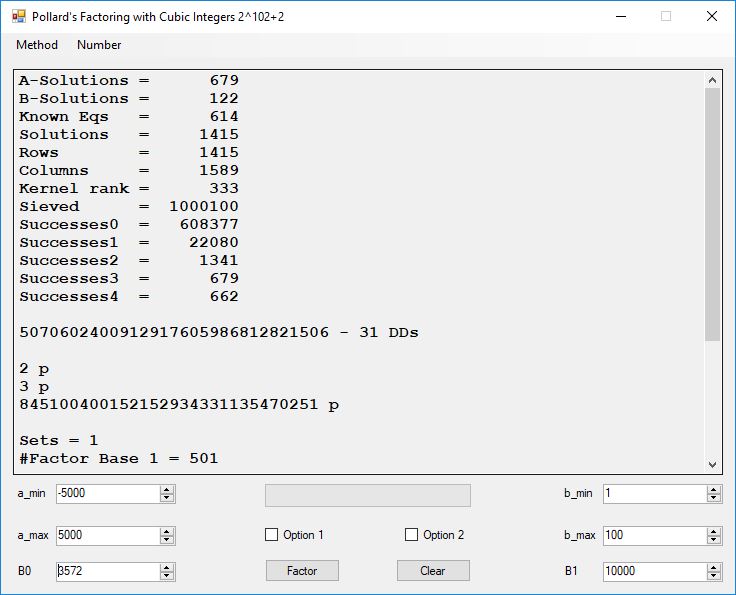
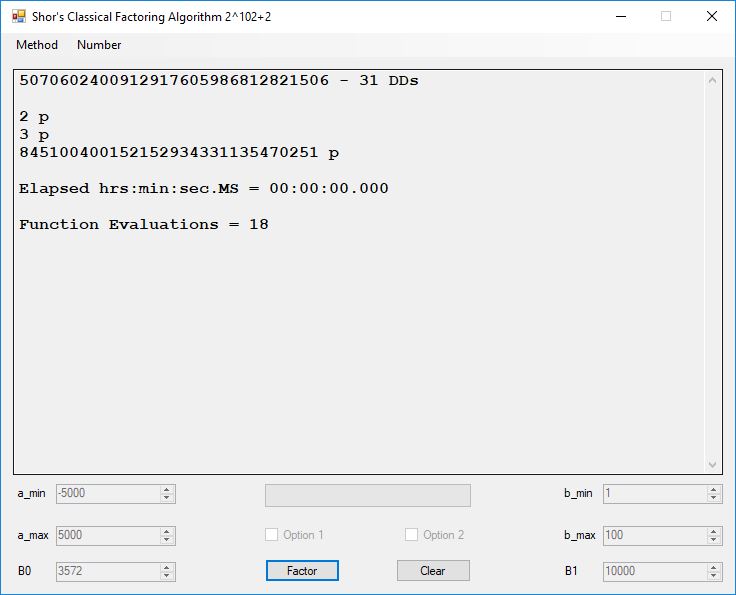
cs7cubic cs7shor

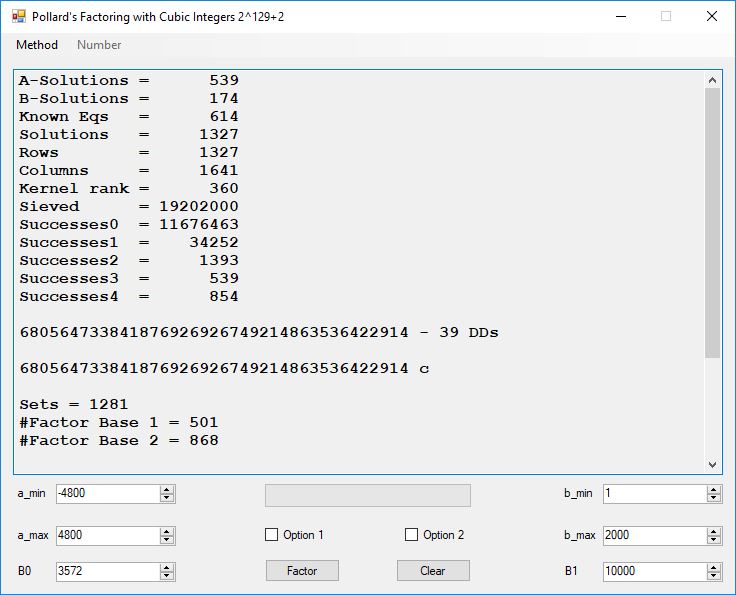
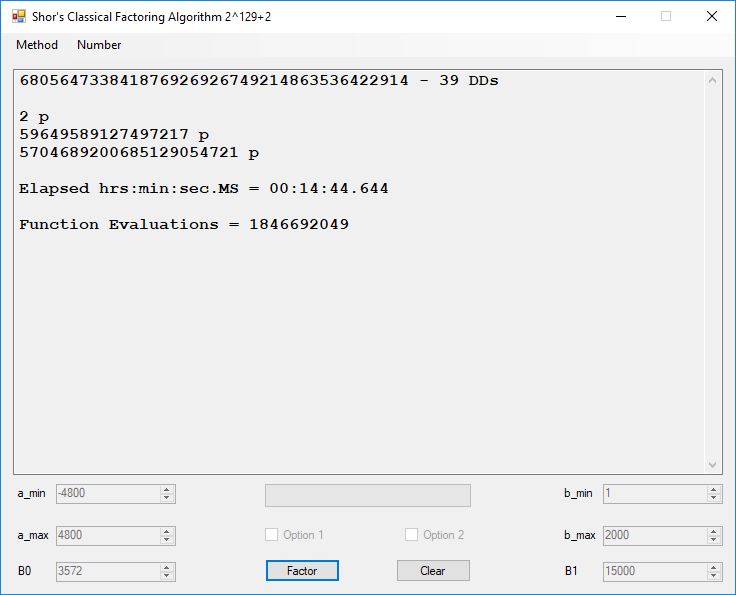
cs8cubic cs8shor

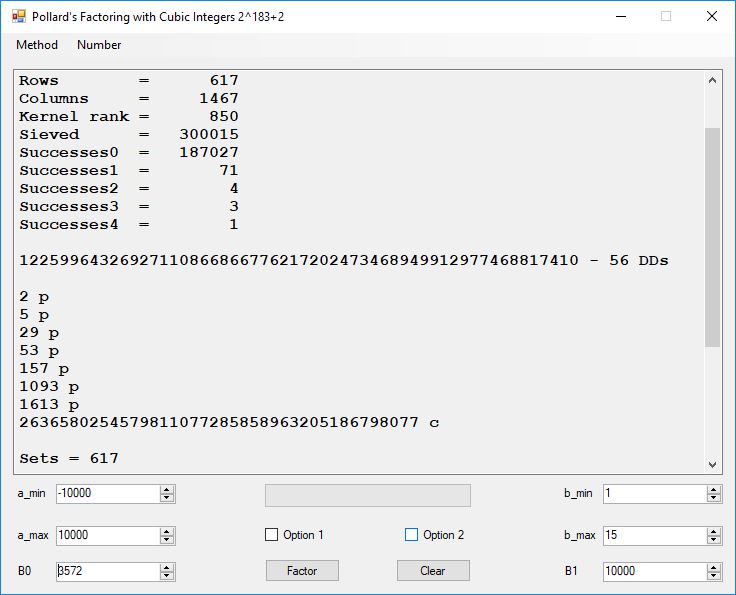
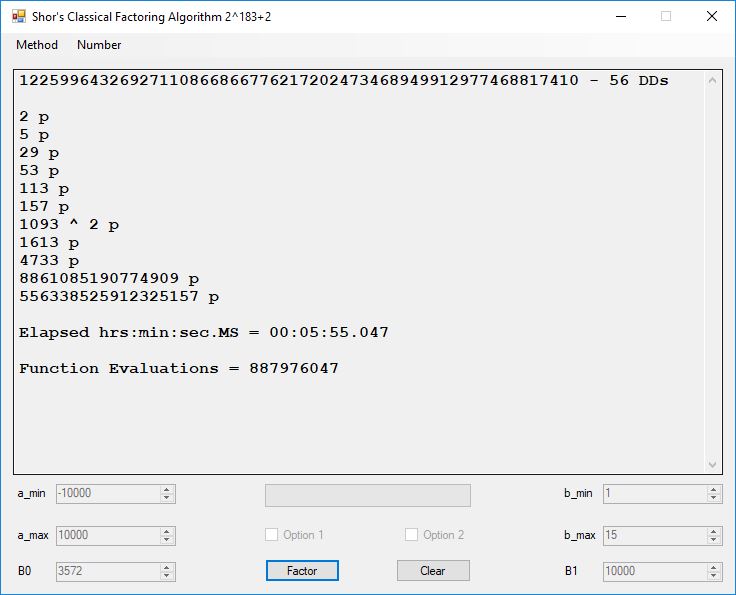
cs9cubic cs9shor

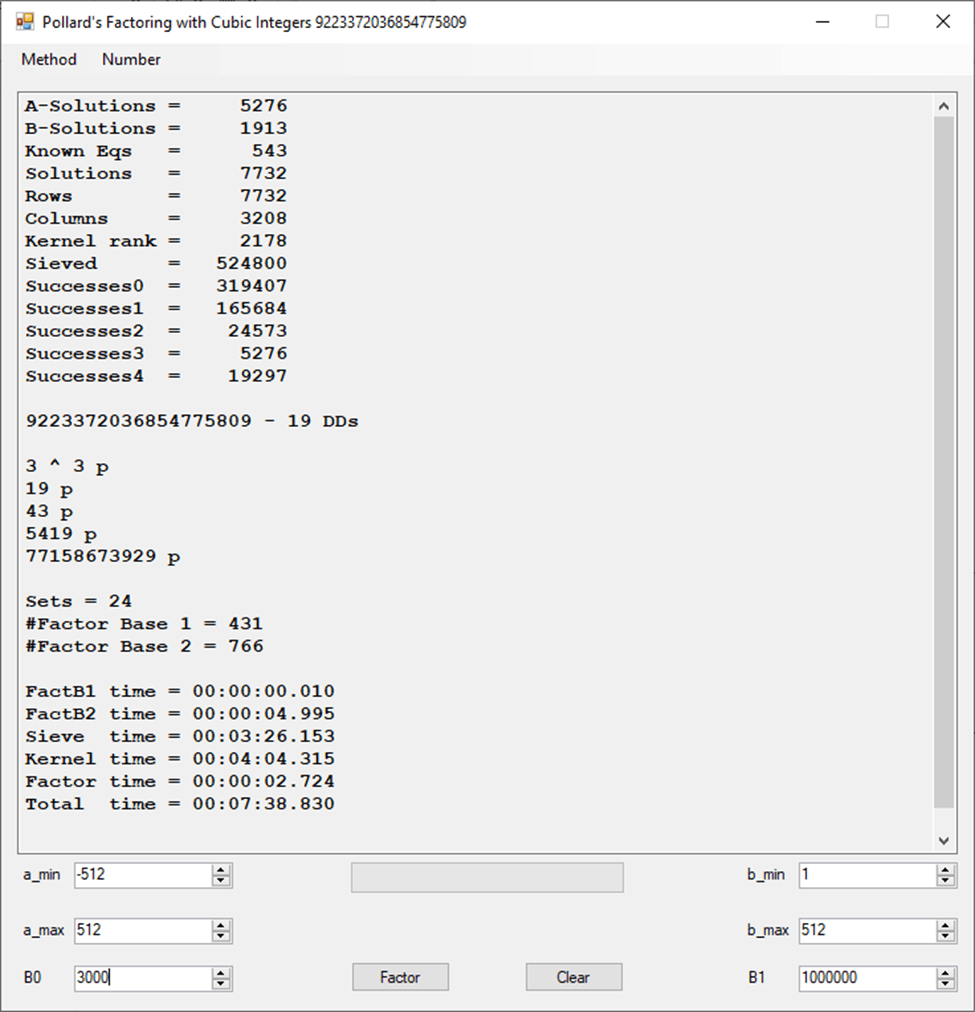
Typical full output from factoring with cubic integers:

A-Solutions = 973
B-Solutions = 234
Known Eqs = 614
Solutions = 1821
Rows = 1821
Columns = 1701
Kernel rank = 423
Sieved = 326434
Successes0 = 200863
Successes1 = 47073
Successes2 = 2708
Successes3 = 973
Successes4 = 1735

2417851639229258349412354 - 25 DDs

2 p
65537 p
414721 p
44479210368001 p

Sets = 189
#Factor Base 1 = 501
#Factor Base 2 = 868

FactB1 time = 00:00:00.000
FactB2 time = 00:00:05.296
Sieve time  = 00:00:17.261
Kernel time = 00:00:06.799
Factor time = 00:00:02.327
Total time  = 00:00:31.742

A-solutions have no large prime. B-solutions have a large prime between B0 and B1 exclusively which is this case is between 3272 and 50000 exclusively. The known equations are between the rational primes and the cubic primes and their associates of the form p = 6k + 1 that have -2 as a cubic residue. There are 81 rational primes of the form and 243 cubic primes but we keep many other associates of the cubic primes so more a and b pairs are successfully algebraically factored. In out case the algebraic factor base has 868 members. The rational prime factor base also includes the negative unit -1. The kernel rank is the number of independent columns in the matrix. The number of dependent sets is equal to columns – rank which is this case 1701 – 423 = 1278. The number of (a, b) pairs sieved is 326434. Successes0 is the pairs that have gcd(a, b) = 1. Successes1 is the number of (a, b) pairs such that a+b*r is B0-smooth or can be factored by the first 500 primes and the negative unit. r is equal to 2^27. Successes2 is the number of (a, b) pairs whose N[a, b] = a^2-2*b^3 can be factored using the norms of the algebraic primes. Successes3 is the number of A-solutions that are algebraically and rationally smooth. Successes4 is the number of B-solutions without combining to make the count modulo 2 = 0. Successes3 + Successes4 should equal Successes2 provided all proper algebraic primes and their associates are utilized.

Note factoring with cubic integers is very fickle with respect to parameter choice.