This is a heavily edited version of an earlier blog entry of Wednesday February 2, 2022.
Tag: Computer Science
Some Recordings Using SONAR Platinum by James Pate Williams Jr
Classical Shor’s Algorithm Versus J. M. Pollard’s Factoring with Cubic Integers
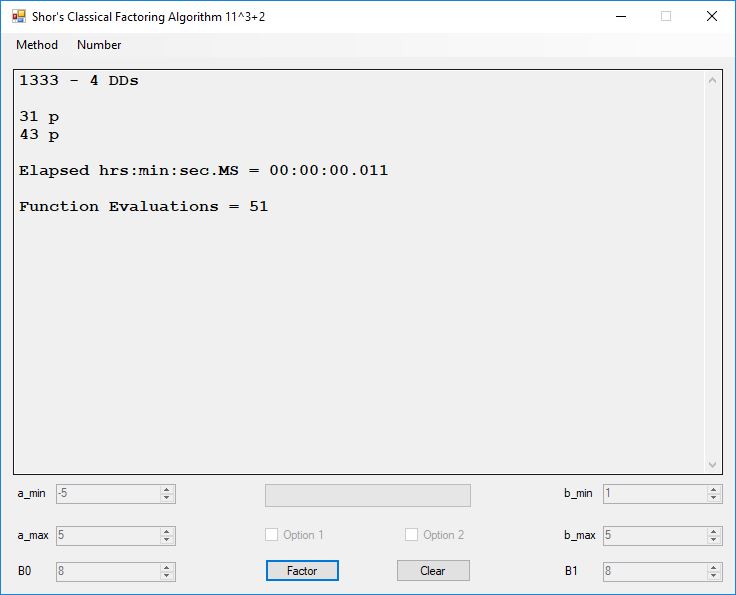
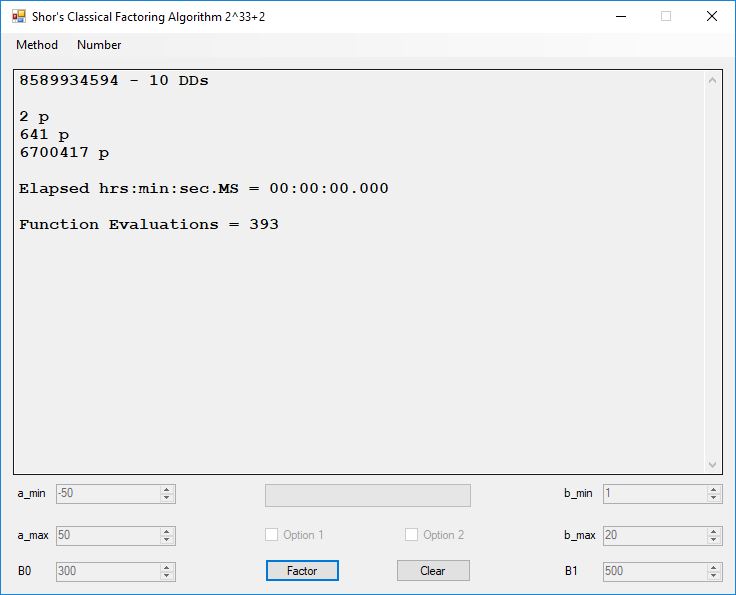
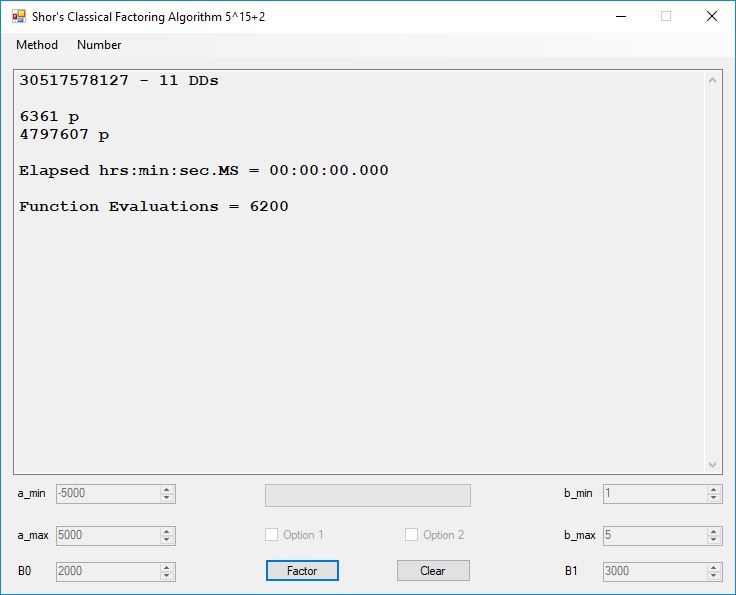
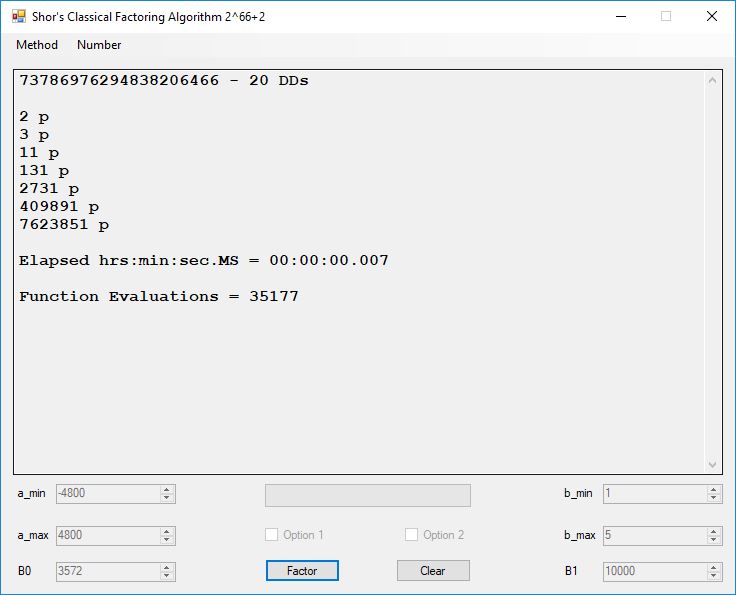
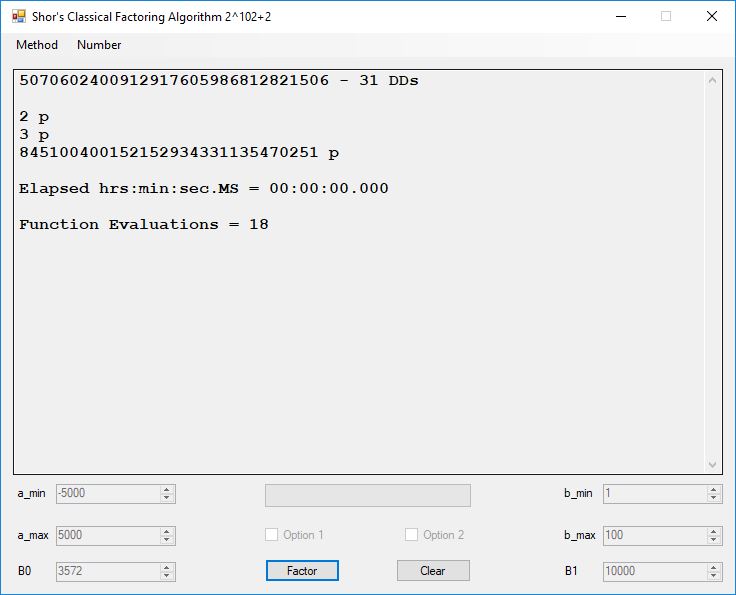
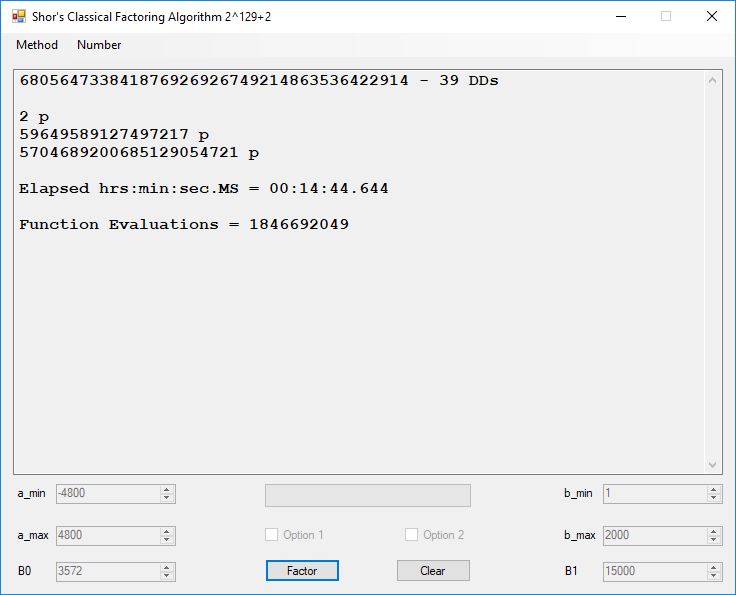
We tried to factor the following numbers with each algorithm: 11^3+2, 2^33+2, 5^15+2, 2^66+2, 2^72+2, 2^81+2, 2^101+2, 2^129+2, and 2^183+2. Shor’s algorithm fully factored all of the numbers. Factoring with cubic integers fully factored all numbers except 2^66+2, 2^71+2, 2^129+2, and 2^183+2.
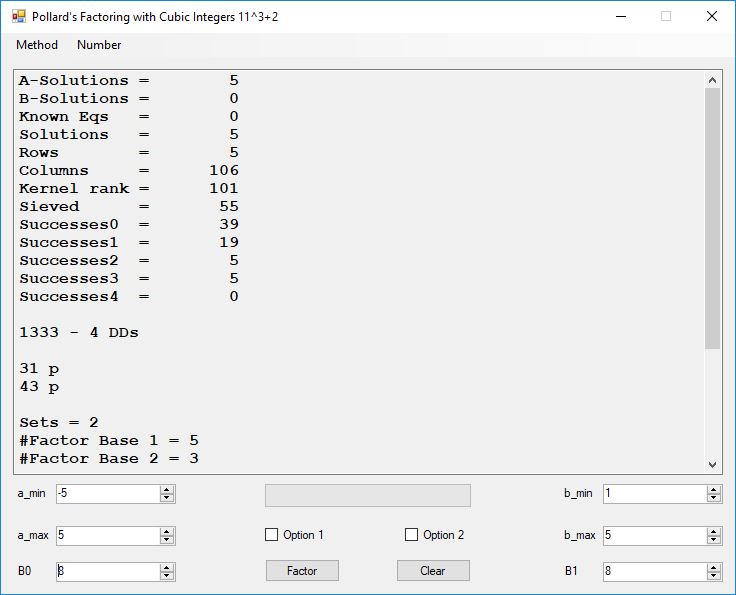
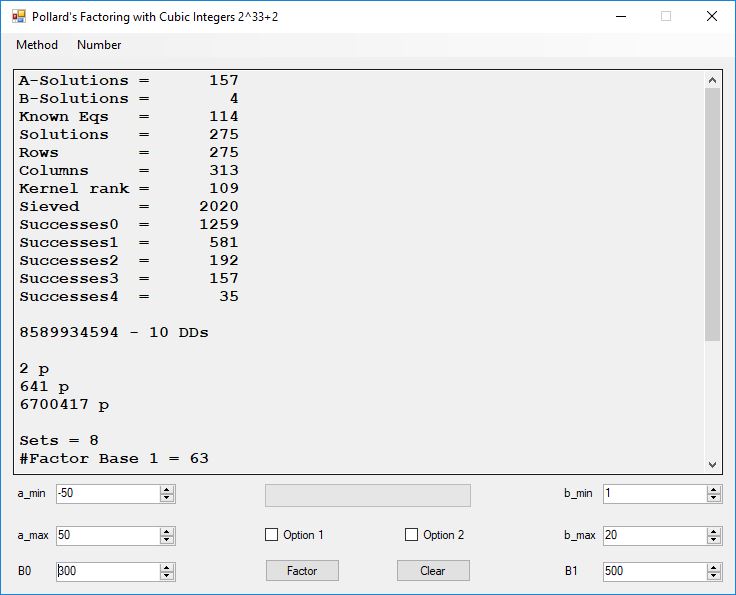
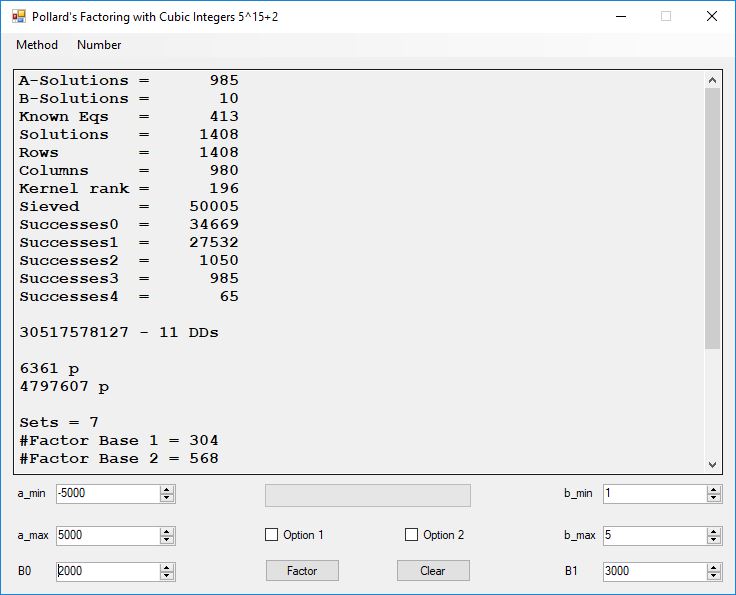
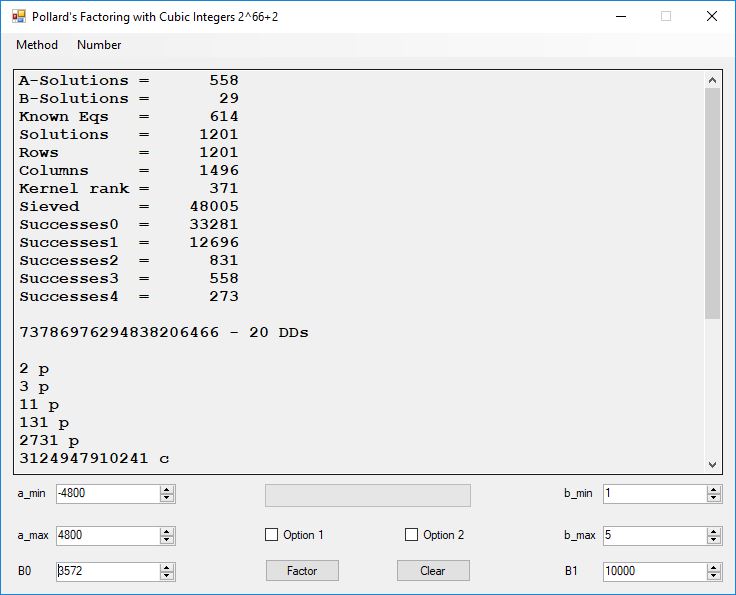
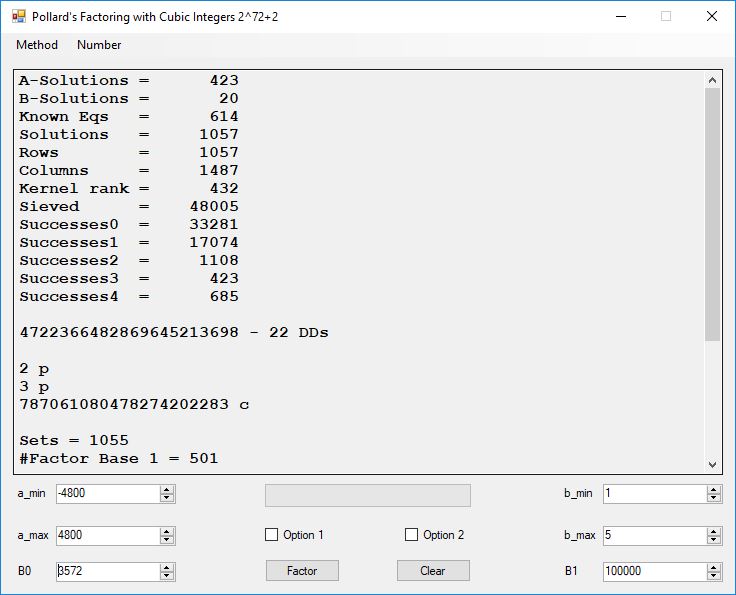
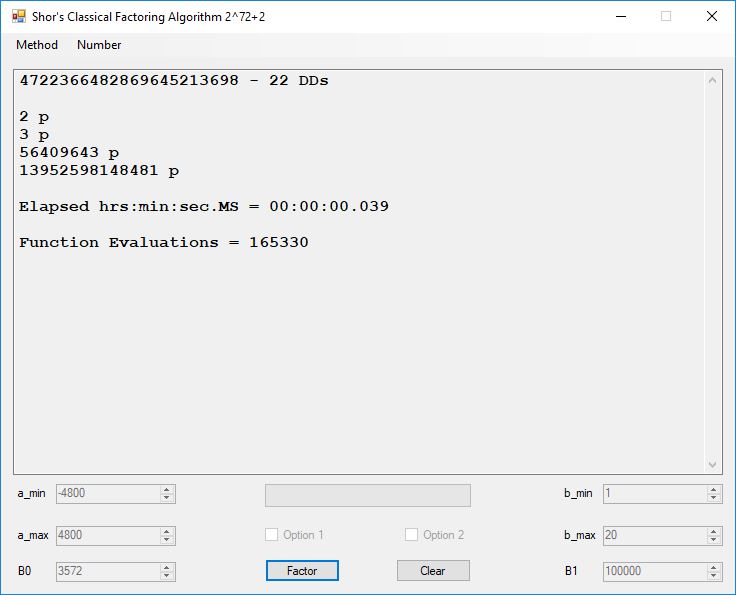
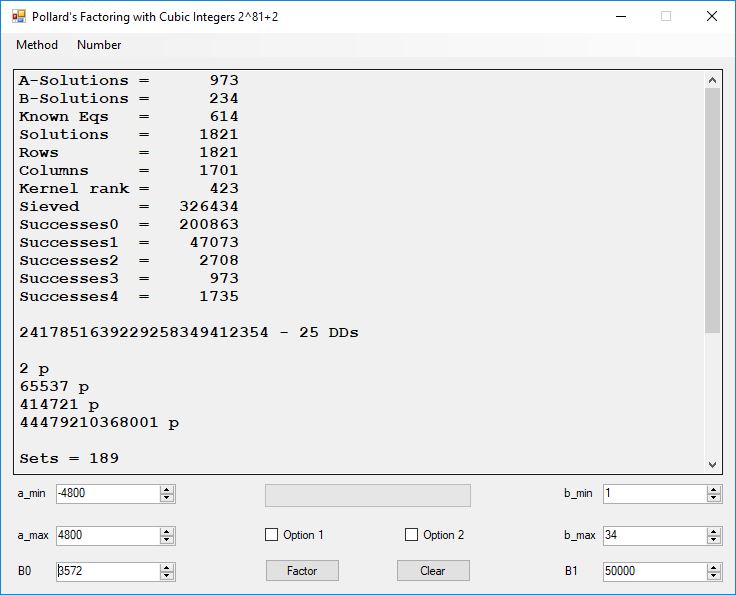
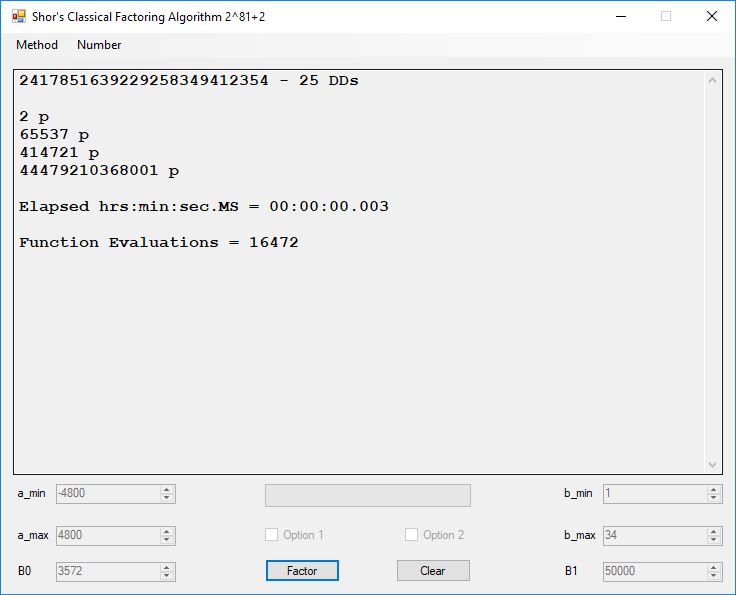
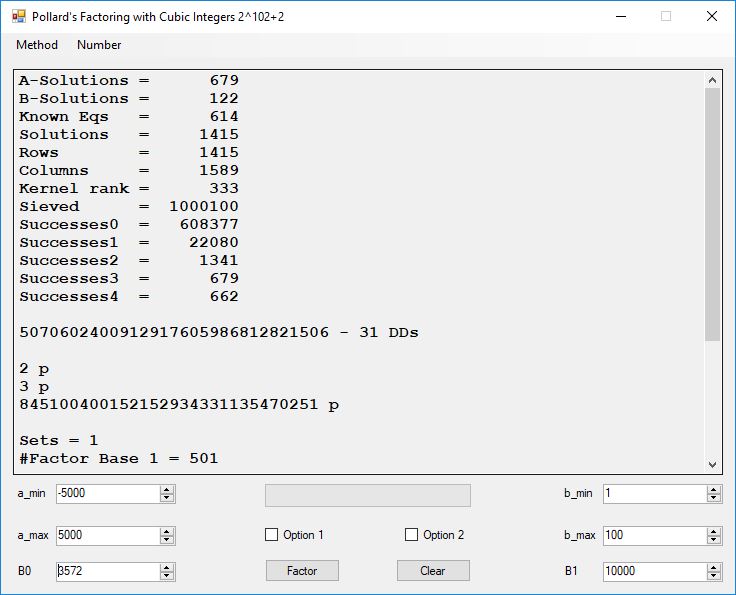
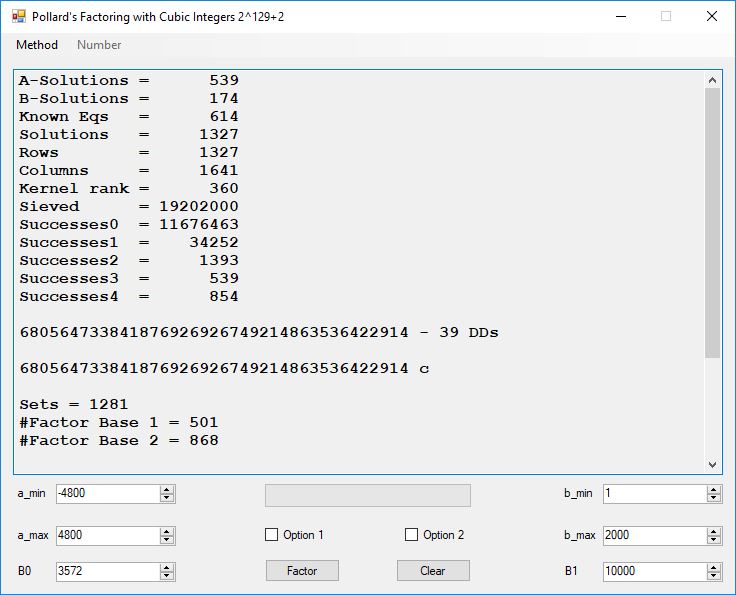
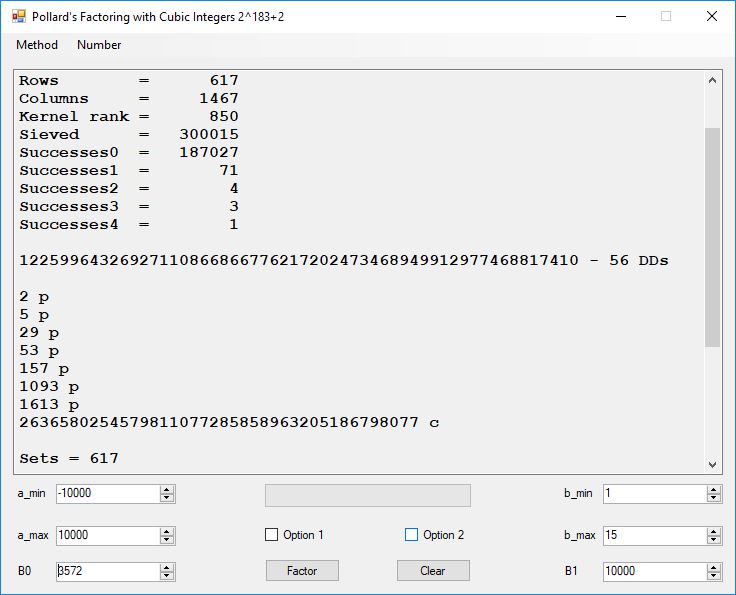
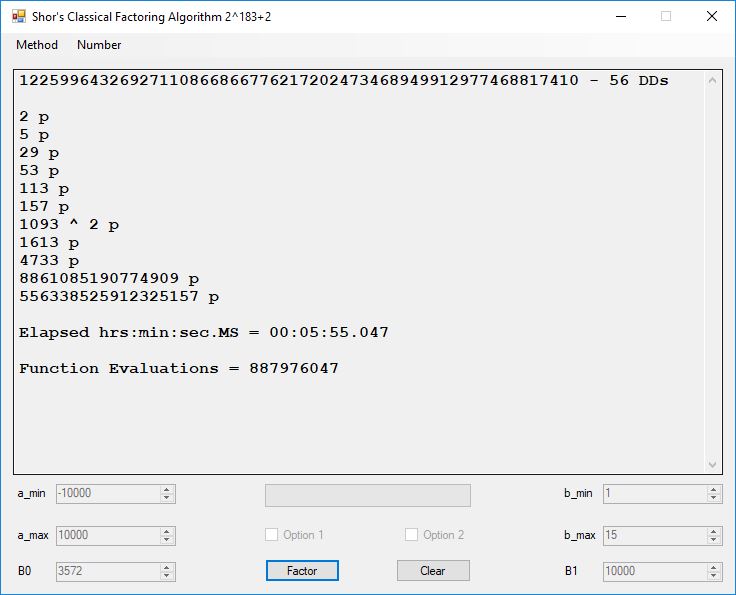
Typical full output from factoring with cubic integers:
A-Solutions = 973 B-Solutions = 234 Known Eqs = 614 Solutions = 1821 Rows = 1821 Columns = 1701 Kernel rank = 423 Sieved = 326434 Successes0 = 200863 Successes1 = 47073 Successes2 = 2708 Successes3 = 973 Successes4 = 1735 2417851639229258349412354 - 25 DDs 2 p 65537 p 414721 p 44479210368001 p Sets = 189 #Factor Base 1 = 501 #Factor Base 2 = 868 FactB1 time = 00:00:00.000 FactB2 time = 00:00:05.296 Sieve time = 00:00:17.261 Kernel time = 00:00:06.799 Factor time = 00:00:02.327 Total time = 00:00:31.742
A-solutions have no large prime. B-solutions have a large prime between B0 and B1 exclusively which is this case is between 3272 and 50000 exclusively. The known equations are between the rational primes and the cubic primes and their associates of the form p = 6k + 1 that have -2 as a cubic residue. There are 81 rational primes of the form and 243 cubic primes but we keep many other associates of the cubic primes so more a and b pairs are successfully algebraically factored. In out case the algebraic factor base has 868 members. The rational prime factor base also includes the negative unit -1. The kernel rank is the number of independent columns in the matrix. The number of dependent sets is equal to columns – rank which is this case 1701 – 423 = 1278. The number of (a, b) pairs sieved is 326434. Successes0 is the pairs that have gcd(a, b) = 1. Successes1 is the number of (a, b) pairs such that a+b*r is B0-smooth or can be factored by the first 500 primes and the negative unit. r is equal to 2^27. Successes2 is the number of (a, b) pairs whose N[a, b] = a^2-2*b^3 can be factored using the norms of the algebraic primes. Successes3 is the number of A-solutions that are algebraically and rationally smooth. Successes4 is the number of B-solutions without combining to make the count modulo 2 = 0. Successes3 + Successes4 should equal Successes2 provided all proper algebraic primes and their associates are utilized.
Note factoring with cubic integers is very fickle with respect to parameter choice.
Classical Shor’s Algorithm
Shor’s algorithm is a fast method of factoring integers using a quantum computer:
https://en.wikipedia.org/wiki/Shor%27s_algorithm
I have implemented the algorithm classically and performed a few experiments on integers greater than equal 12. I used Floyd’s cycle finding algorithm as implemented with a randomized Pollard’s Rho Factoring method using two second degree polynomials:
https://en.wikipedia.org/wiki/Pollard%27s_rho_algorithm
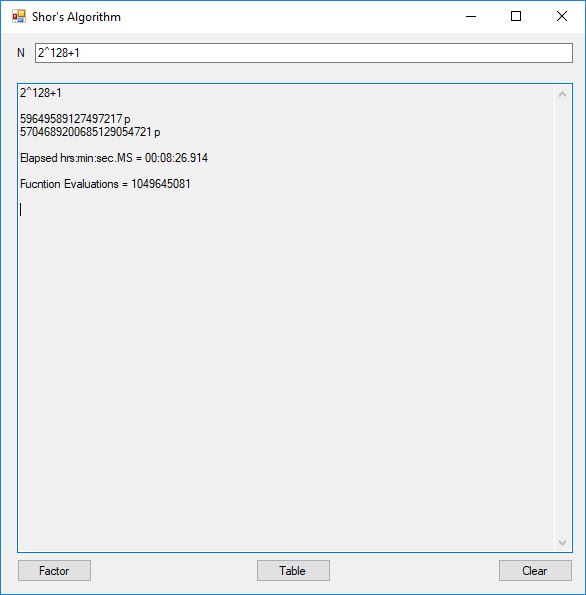
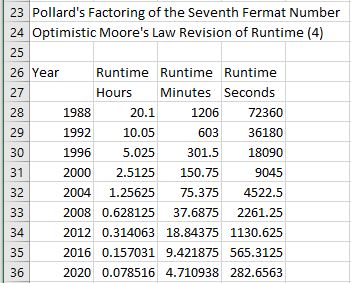
I factored the seventh Fermat number in less than nine minutes. J. M. Pollard factored this number in 20.1 hours in 1988 using the special number field sieve [see “Lecture Notes in Mathematics 1554 The Development of the Number Field Sieve” edited by A. K. Lenstra and H. W. Lenstra, Jr. The paper by Pollard is entitled “Factoring with Cubic Integers”]. Both Pollard and I used personal computers.
Suppose Moore’s original law is applied to Pollard’s factoring of the seventh Fermat number and also assume computing time is cut in half every two years then we can compute the following table:

A less optimistic table states that the computation time is halved every four years:
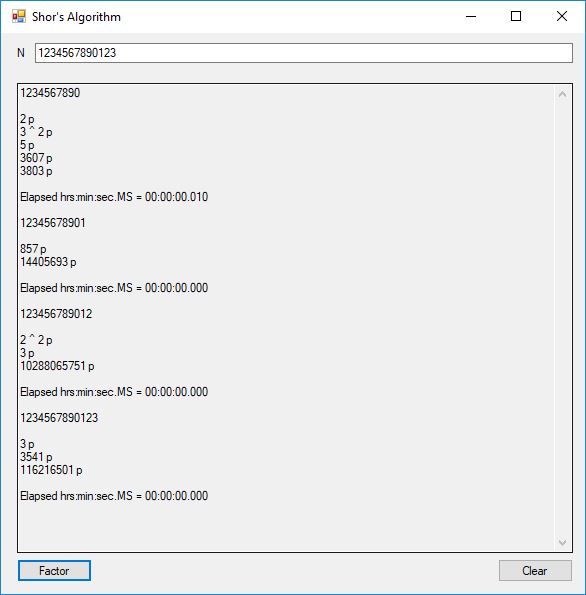
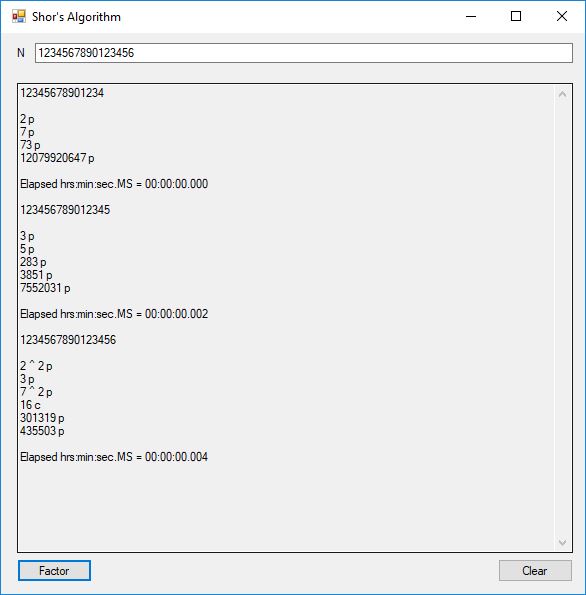
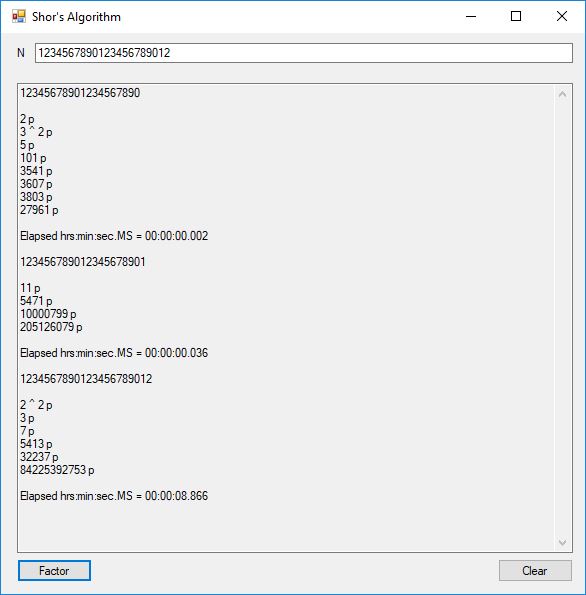
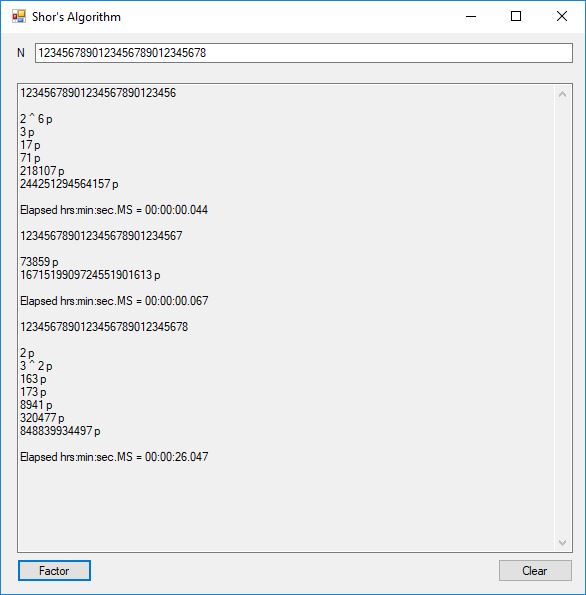
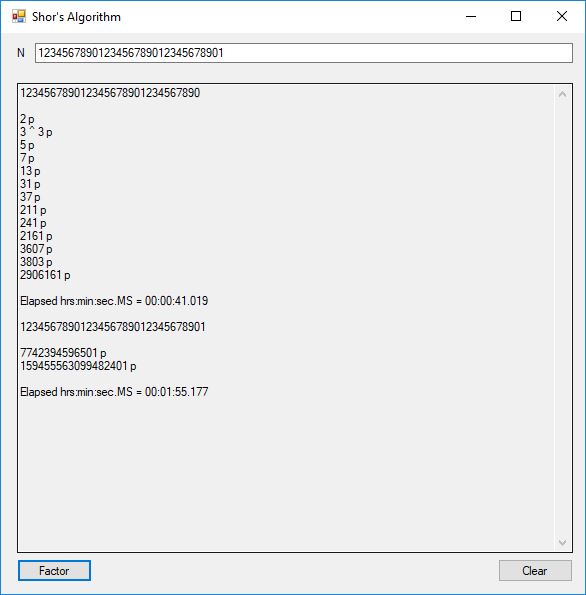
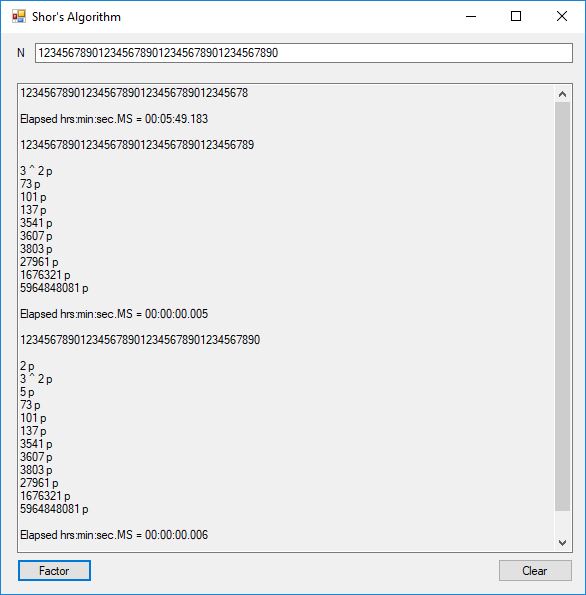
I successfully factored 38 of 39 numbers of the form 12, 123, 1234, 12345, … , 1234567890123456789012345678901234567890. The results of my factoring C# Windows form application are displayed below:
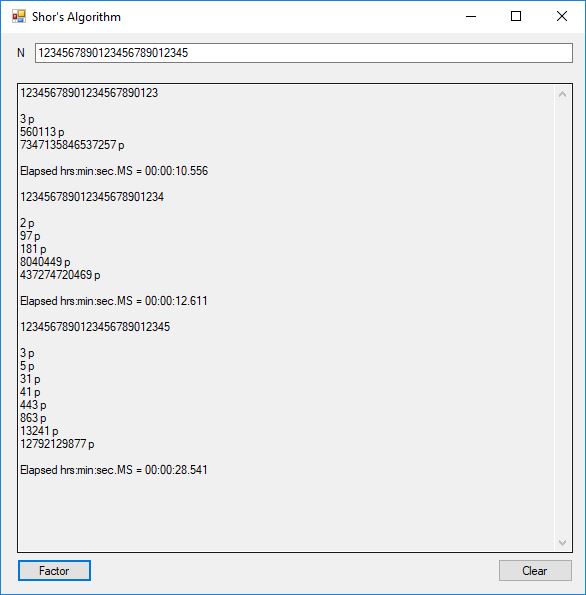
I was eventually able to factor the 38-decimal digit number that failed in the above calculation as illustrated below:
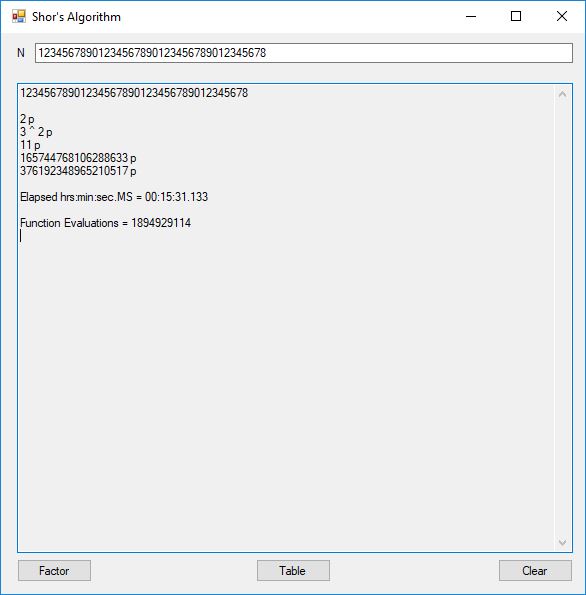
The number of bits per number varied from 4-bits to 130-bits. This is still no where near the ability to factor a 3,000-bit Rivest-Shamir-Adleman composite integer so most financial systems remain secure. The link below will take you to the Microsoft C# project directory on my OneDrive account.
https://1drv.ms/f/s!AjoNe9CiN2M9gfMbQ8H_g3GMQEC6iA
The C# source code is at the preceding link in a printable and readable PDF.
Root Finding Algorithms by James Pate Williams, BA, BS, MSwE, PhD
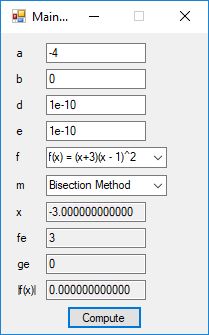
We designed and implemented a C# application that uses the following root finding algorithms:
- Bisection Method
- Brent’s Method
- Newton’s Method
- Regula Falsi
https://en.wikipedia.org/wiki/Bisection_method
https://en.wikipedia.org/wiki/Brent%27s_method
https://en.wikipedia.org/wiki/Newton%27s_method
https://en.wikipedia.org/wiki/False_position_method
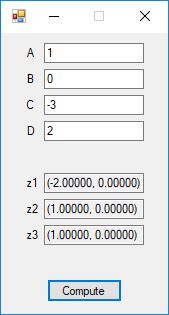
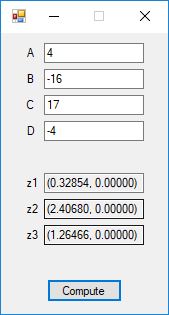
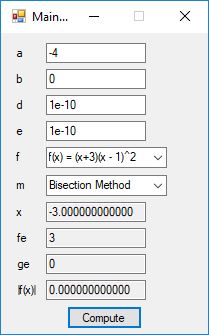
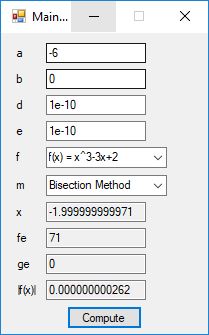
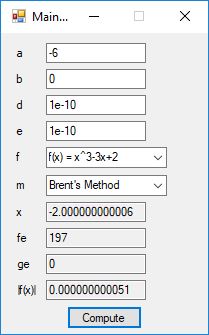
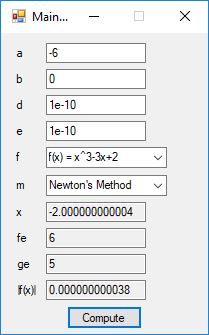
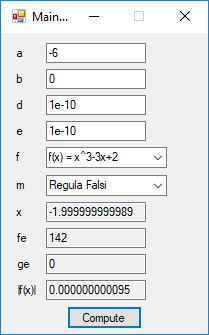
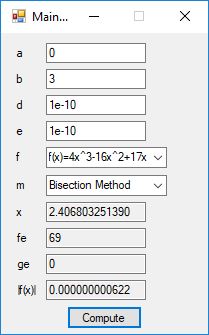
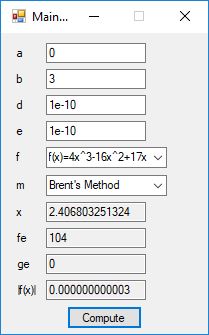
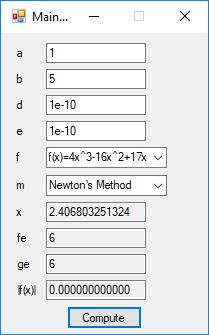
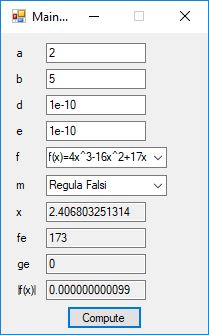
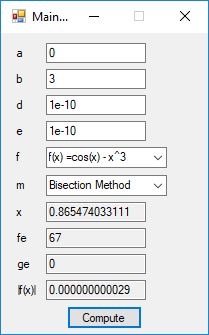
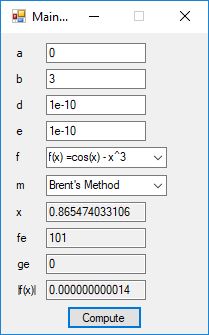
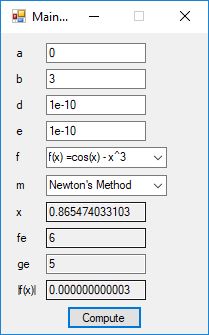
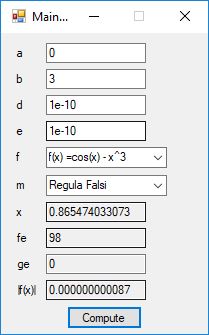
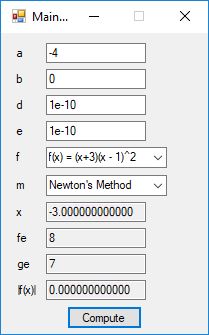
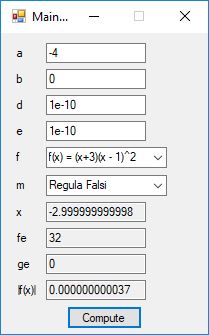
The source code files are displayed below as Word files:
Roots of Small Degree Polynomials with Real Coefficients by James Pate Williams, BA, BS, MSwE, PhD
We designed and implemented quadratic formula, cubic formula, and quartic formula solvers using the formulas in the Wikipedia articles:
https://en.wikipedia.org/wiki/Quadratic_formula
https://en.wikipedia.org/wiki/Cubic_function
https://en.wikipedia.org/wiki/Quartic_function
We tested our C# implementation against:
https://keisan.casio.com/exec/system/1181809415
http://www.wolframalpha.com/widgets/view.jsp?id=3f4366aeb9c157cf9a30c90693eafc55
https://keisan.casio.com/exec/system/1181809416
Here are screenshots of the C# application:
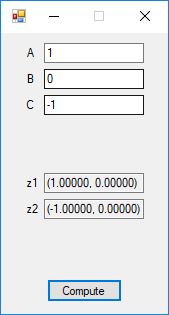
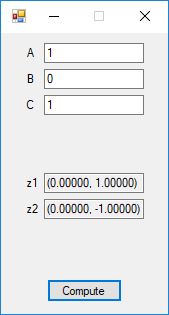
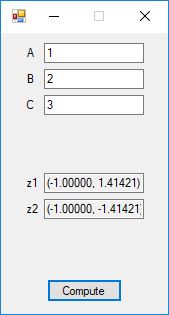
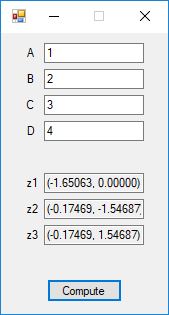
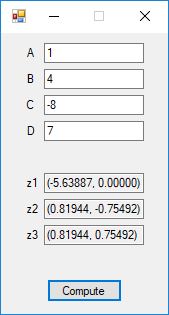
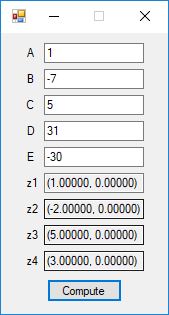
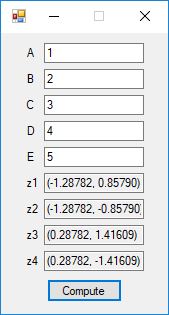
C# source code files for the application:
The Bailey-Borwein-Plouffe Formula for Calculating the First n Digits of Pi
The Bailey-Borwein-Plouffe formula for determining the digits of pi was discovered in 1995. This formula has been utilized to find the exact digits of pi to many decimal places.
I recently re-implemented my legacy C and FreeLIP program that utilized the BBP formula. The new C# application uses a homegrown big unsigned decimal number package that includes methods for +, -, *, / operators and an exponentiation (power) function. I used short integers (16-bit signed integers) to represent the individual digits of the number in any base whose square can be expressed as a positive short integer. That includes the decimal base 10 and hexadecimal base 16. For this application the base was chosen to be 10. Also, included was a n-digits of pi function that used the C# language’s built-in BigInteger data type. Below are some screen shots of the program in action.
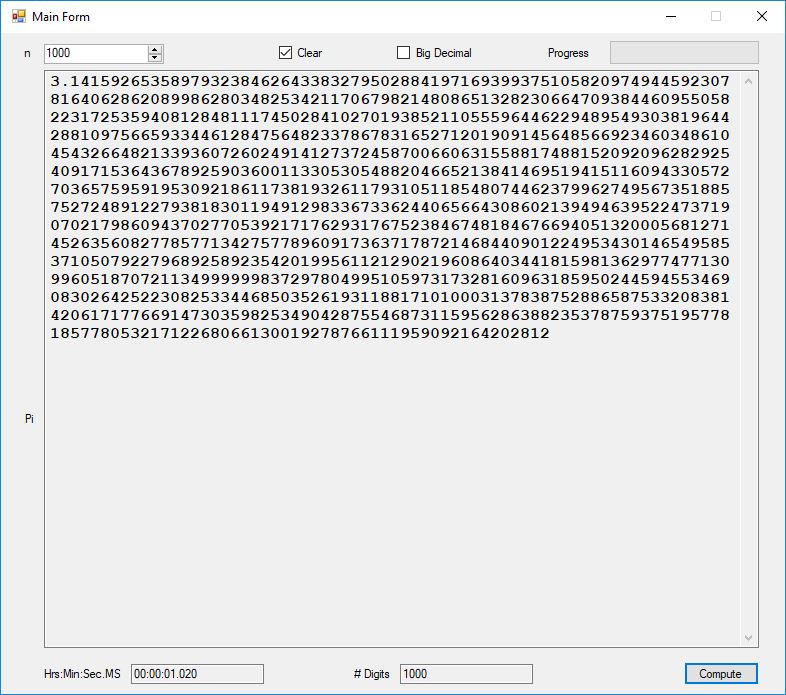
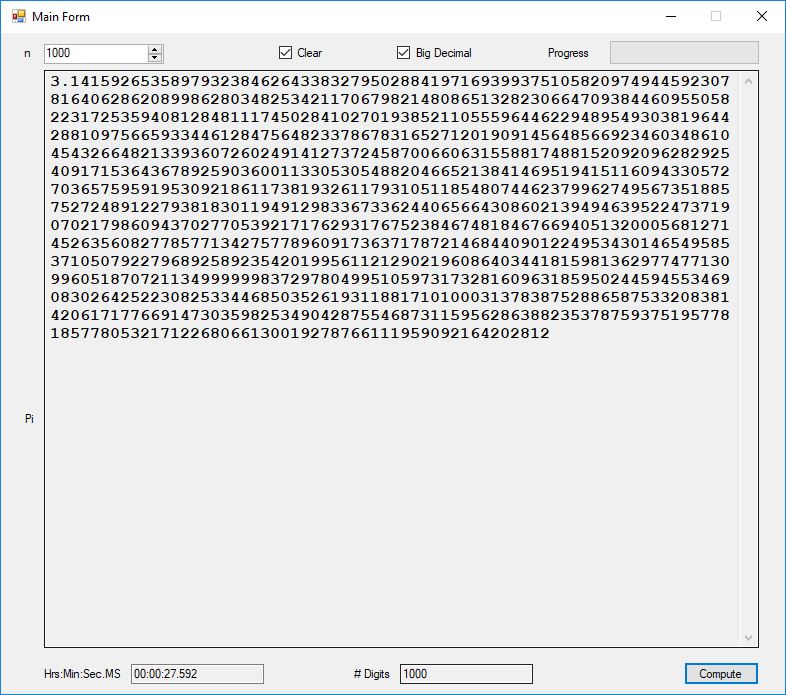
As you can easily see the BigInteger implementation is an order of magnitude faster that the BigDecimal version (actually around 27+ times faster).
Last, we include a link to a PDF containing data comparing calculations performed on a Intel based desktop versus an AMD based laptop.
Microsoft Outlook Add-In by James Pate Williams, Jr. BA, BS, MSwE, PhD
After successfully downloading and installing a free one-month trial evaluation version of Microsoft’s Visual Studio 2017 Professional Graphical User Interface Integrated Development Environment, I decided to try my hand at creating an Office VSTO Add-In. I chose the computer language C# and the Office application Outlook. Among other functions Outlook is a personal computer’s email client for IMAP or POP3. The problem that the add-in solves is a preliminary evaluation of the meaning of an email’s body. The add-in counts the frequency of occurrence of the following (assuming English language):
- Characters
- Lines Separated by CR/LF
- Words
- Danger Words – words that indicate danger to the author and/or other people, places, or things
- Cuss or Curse Words
- Hate and Objectionable Words
- Lower Case Characters
- Upper Case Characters
- Numeric Characters
- Consonant Count Including ‘y’
- Vowel Count Excluding the Sometimes ‘y’
- Punctuation Count {‘.’, ‘,’, ‘;’, ‘:’, ‘?’, ‘!’}
Once an email is opened and in an active inspector the OutlookAddIn1’s Outlook ribbon is displayed with 12 edit boxes that contain the counts enumerated in the preceding numbered list. Below is an email that illustrates night of the frequency tabulations.
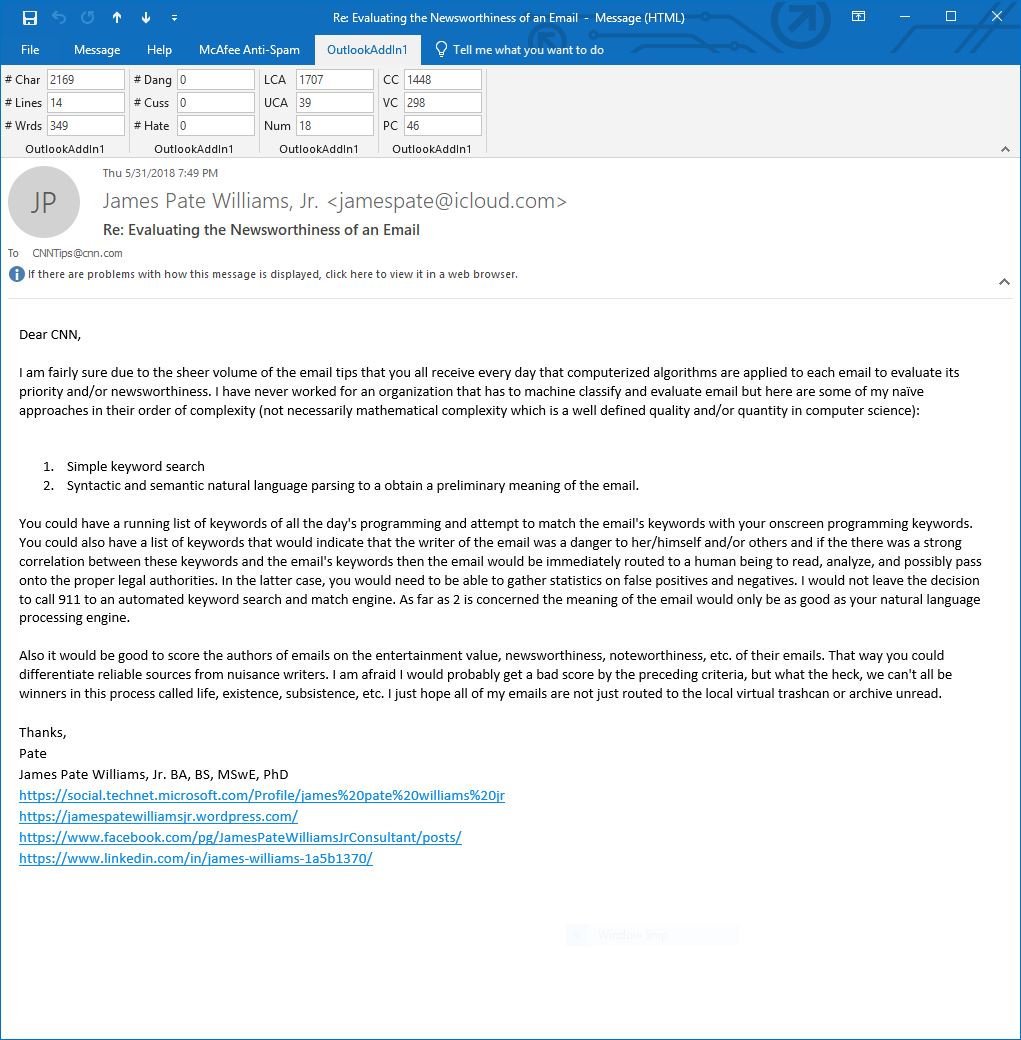
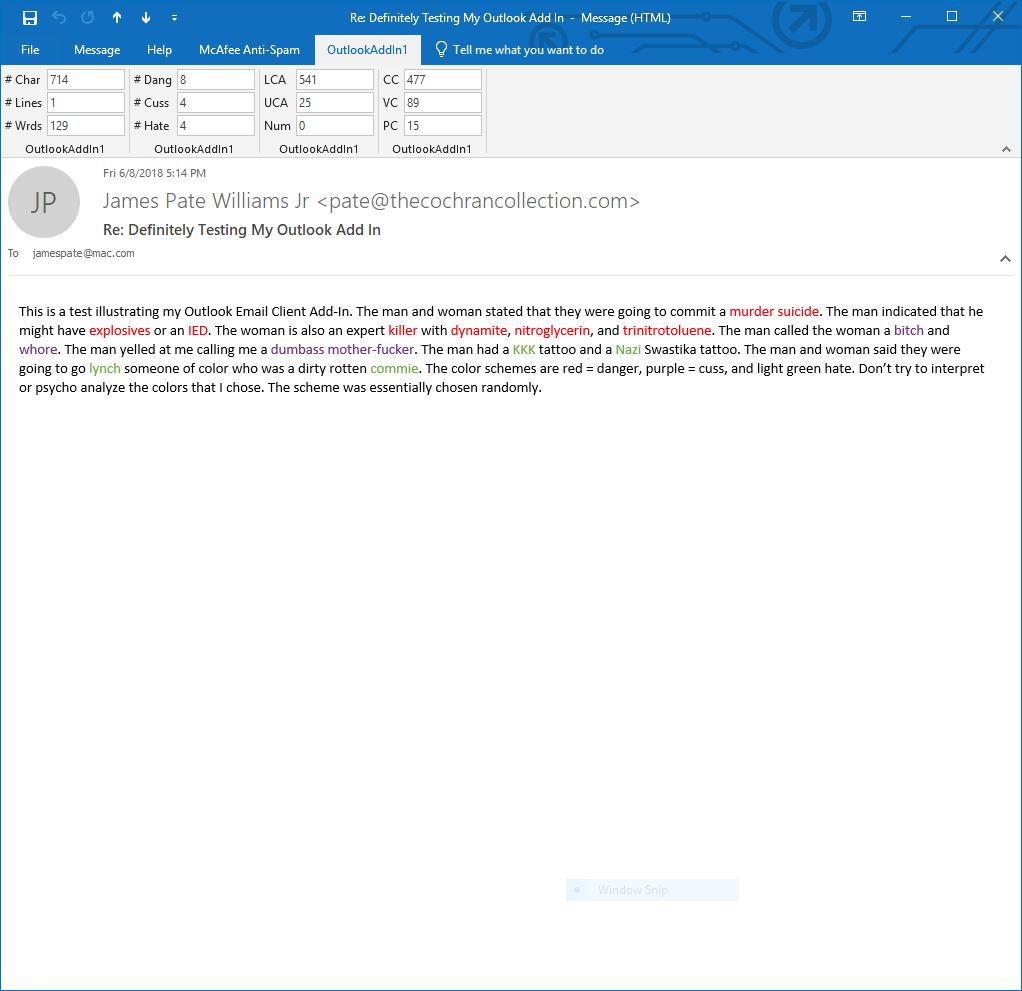
The next email contains danger, cuss, and hate words.
https://social.technet.microsoft.com/Profile/james%20pate%20williams%20jr
https://www.facebook.com/pg/JamesPateWilliamsJrConsultant/posts/
Five Stream Ciphers Created from Five Pseudorandom Number Generators Built Using the Tests of FIPS 140-1 by James Pate Williams, BA, BS, MSwE, PhD
The five pseudorandom number generators are:
- Triple-AES based ANSI X9.17 PRNG
- Triple-DES based ANSI x9.17 PRNG
- RSA based PRNG
- Micali-Schnorr PRNG
- Blum-Blum-Shub PRNG
Five stream ciphers were created using 1 to 5. Screenshots of the C# application follow:
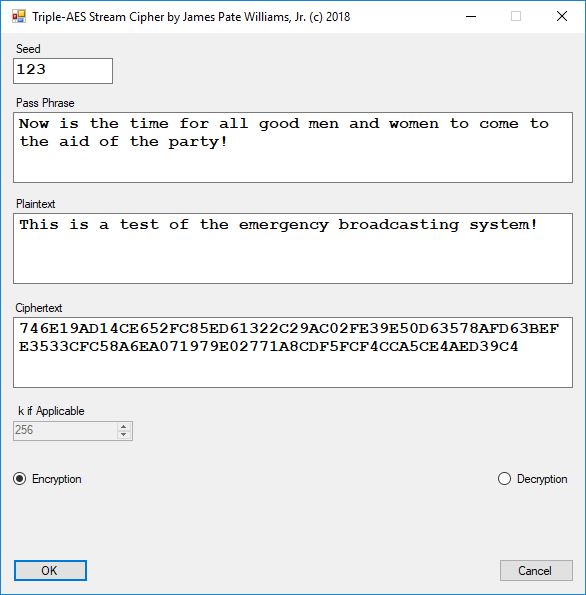
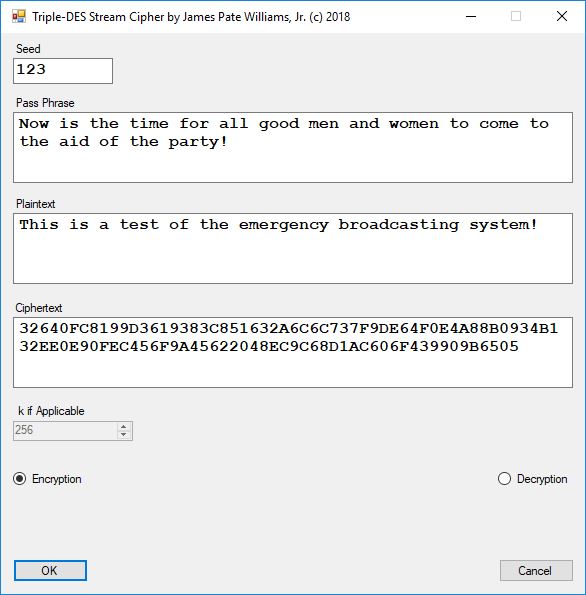
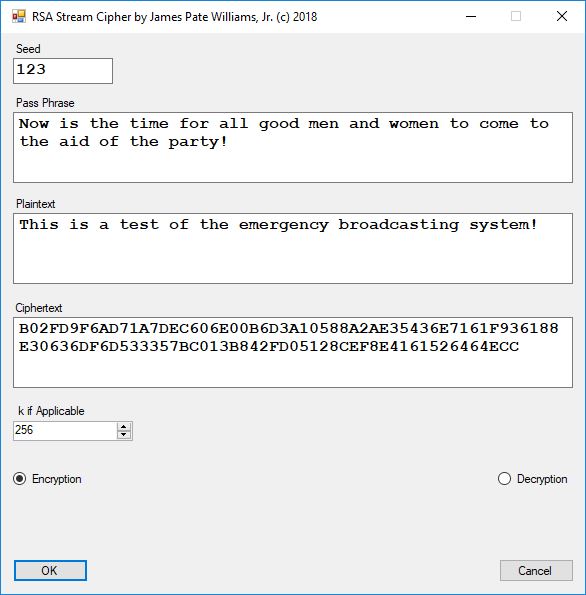
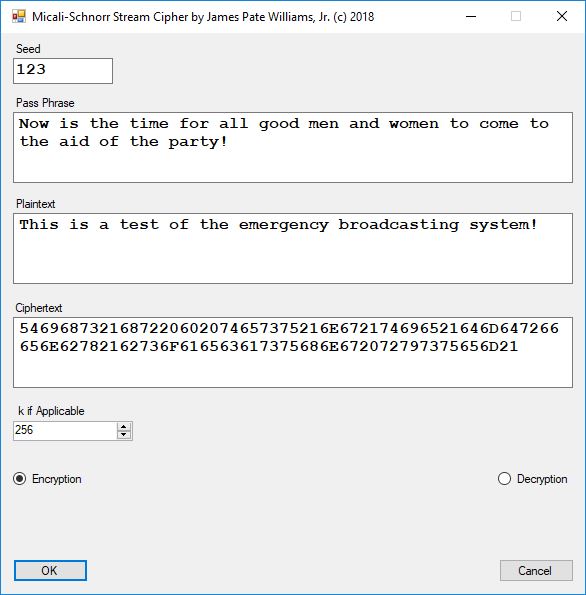
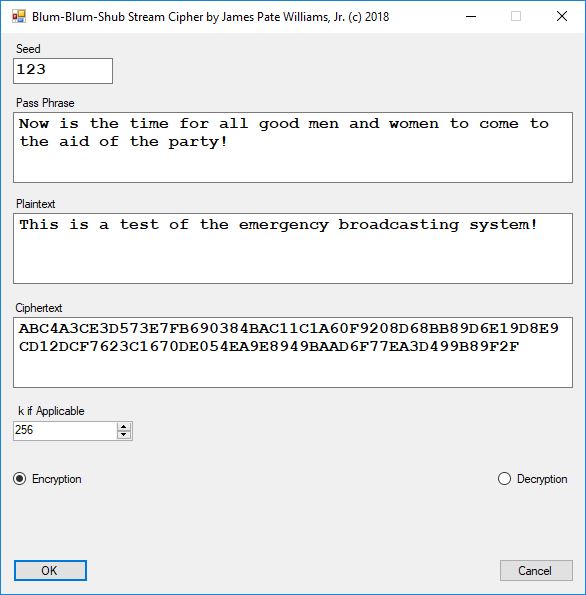
The pass phrase optimally should consist of 147 ASCII characters. If the number of pass phrase ASCII characters is less than 147 then more random ASCII characters are added using the standard C# pseudorandom number generator seeded with the parameter named Seed. The user defined parameter k is used by RSA, Micali-Schnorr, and Blum-Blum-Shub pseudorandom number generators. It is the approximate bit length of the large composite number composed of two large probable prime numbers. The real key lengths of all the stream ciphers is about 1024-bits for 1, 3, 4, and 5 and 296-bits for 2. I’d strongly suggest using 1 and/or 5.
Tests of Six Pseudorandom Number Generators (PRNGs) Using the Now Superseded FIPS 140-1 by James Pate Williams, Jr. BA, BS, MSwE, PhD
This blog explores six pseudorandom number generators which are enumerated as follows:
- Standard C# PRNG
- Triple-AES PRNG
- Triple-DES PRNG
- RSA Based PRNG
- Micali-Schnorr PRNG
- Blum-Blum-Shub PRNG
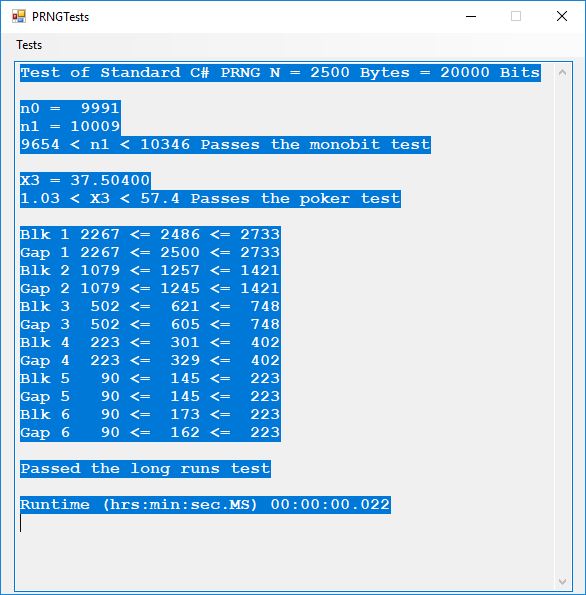
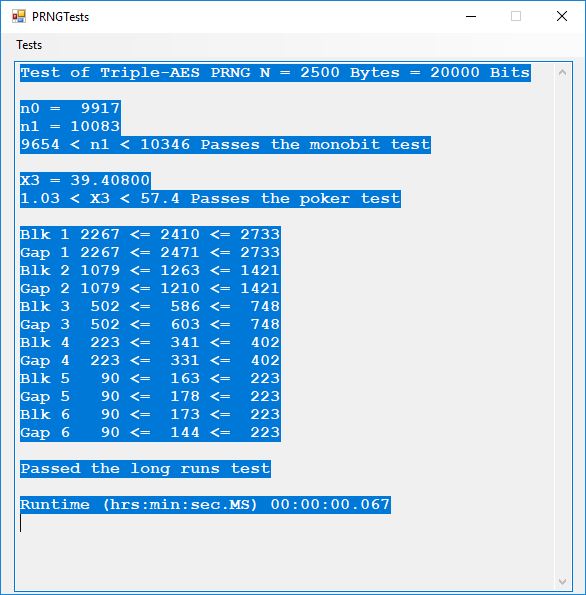
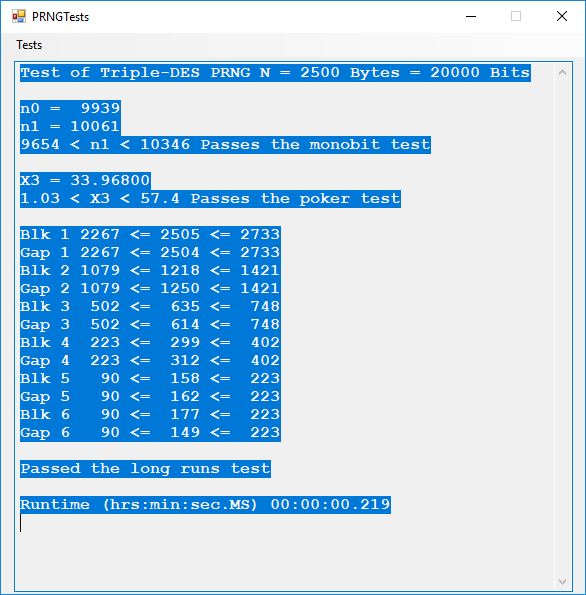
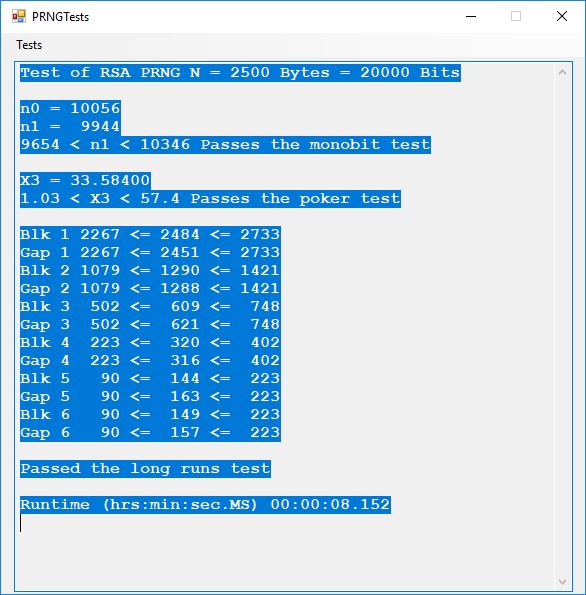
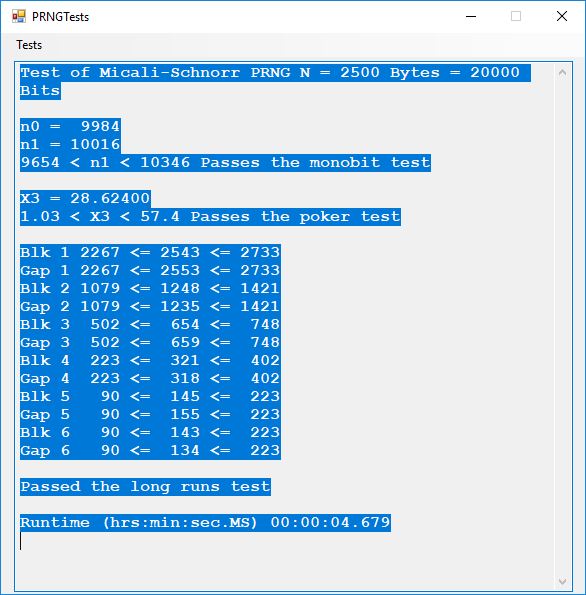
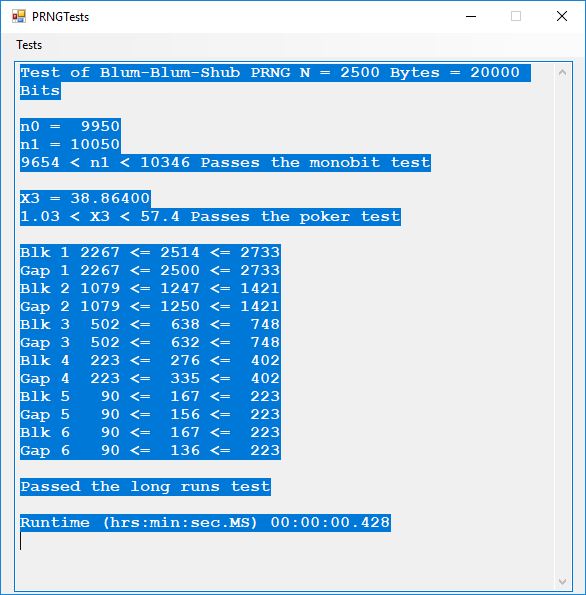
Here is the order in terms of run-times from the fastest to the slowest: 1, 2, 3, 6, 5, 4.