Category: Graph Coloring Problem

The Graph Coloring Problem and N-Queens Puzzle are both NP-Complete constraint satisfaction problems. There does not exist polynomial time algorithms to solve large instances of either problem. The Graph Coloring Problem is given a graph of n-vertices and m-edges find the minimum number of colors such that no two connected vertices are of the same color. The N-Queens Puzzle is given a n-by-n chessboard and n-queens place the queens such that no two queens are attacking one another. A queen in chess can move any number of squares diagonally, horizontally, or vertically.

As a Master of Software Engineering graduate student in the era 1998 to 2000, I majored in the subdiscipline of artificial intelligence known as constraint satisfaction. I developed evolutionary hill-climbing algorithms to solve constraint satisfaction problems. I specifically solved instances of the Graph Coloring Problem and the N-Queens Puzzle. I compared my algorithms with other researchers’ algorithms. One of the algorithms tested was Makato Yokoo’s Weak-Commitment Search Algorithm (WCSA). Yakoo wrote a very nice book named “Distributed Constraint Satisfaction” which has excellent flow-charts of several algorithms including the Min-Conflicts Search Algorithm (MCSA) and his WCSA. I implemented both algorithms in the C++ and Java computer languages.

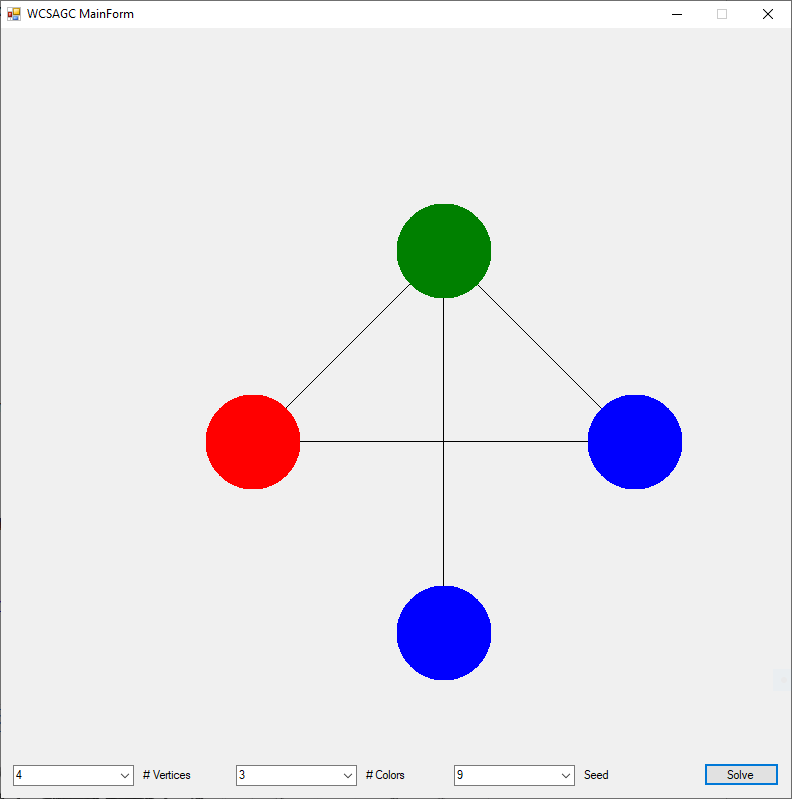
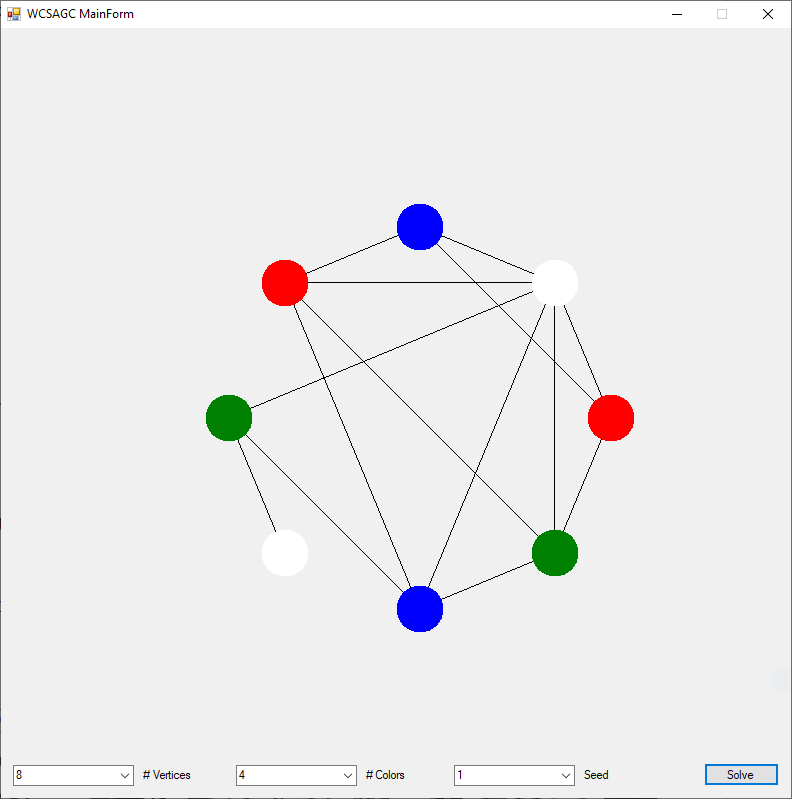
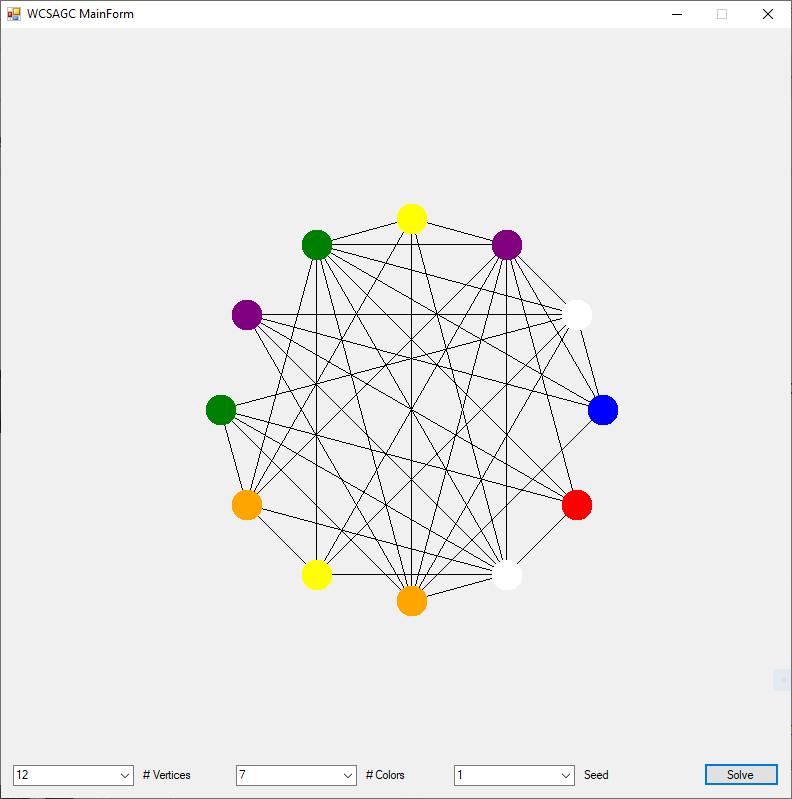
I rewrote the preceding two algorithms in the C# computer language sometime in the epoch 2008 – 2009. Below are three instances of the Graph Coloring Problem with four, eight, and twelve vertices solved by the Yakoo’s WCSA.