A Matrix Identity
Category: Matrix Algebra
Preliminary Factorization Results of the Thirteenth Fermat Number (c) February 5, 2024, by James Pate Williams, Jr.
I am working on a factorization of the Thirteenth Fermat number which is 2 ^ 8192 + 1 and is 2,467 decimal digits in length. I am using Pollard’s factoring with cubic integers on the number (2 ^ 2731) ^ 3 + 2. I am also utilizing a homegrown variant of the venerable Pollard and Brent rho method and Arjen K. Lenstra’s Free LIP Elliptic Curve Method. I can factor the seventh Fermat number 2 ^ 128 + 1 in five to thirty minutes using my C# code. The factoring with cubic integers code is in C and uses Free-LIP.
Fermat factoring status (prothsearch.com)
The following is a run of Lenstra’s ECM algorithm:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^8192+1
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 1
2710954639361 p # digits 13
3603109844542291969 p # digits 19
Runtime (s) = 17015.344000
I aborted the previous computation due to the fact I was curious about the number of prime factors that could be found on personal computer. I will try a lot more calculation time in a future run. My homegrown application is able to at least find the first factor of Fermat Number 13.
Latest Factoring Results (c) February 4, 2024, by James Pate Williams, Jr.
I am testing two factoring algorithms: Pollard-Shor-Williams’s method, a home-grown version of the venerable Pollard rho algorithm and Pollard’s factoring with cubic integers. The second recipe is from “The Development of the Number Field Sieve” edited by Arjen K. Lenstra and Hendrik W. Lenstra, Jr. I use the 20-digit test number, 2 ^ 66 + 2 = 73786976294838206466. My method is very fast with this number as shown below:
2^66+2
73786976294838206466 20
Pseudo-Random Number Generator Seed = 1
Number of Tasks = 1
2 p 1
3 p 1
11 p 2
131 p 3
2731 p 4
409891 p 6
7623851 p 7
Elapsed hrs:min:sec.MS = 00:00:00.652
Function Evaluations = 1995
The Pollard factoring with cubic integers takes a long time but is capable of factoring much larger numbers. The results of the full factorization of my test number are:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^66+2
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 3
73786976294838206466
Enter a lower bound : -50000
Enter a upper bound : +50000
Enter b lower bound : +1
Enter b upper bound : +50000
Enter maximum kernels : 1024
Enter algebraic prime count: 300
Enter rational prime count: 300
Enter lo large prime bound: 10000
Enter hi large prime bound: 11000
Numbers sieved = 452239293
Successes 0 gcd(a, b) is 1 = 274929004
Successes 1 rational smooth a + b * r = 181838258
Successes 2 long long smooth = 68959
Successes 3 kernels tested = 535
2 p # digits 1
3 p # digits 1
11 p # digits 2
131 p # digits 3
2731 p # digits 4
409891 p # digits 6
7623851 p # digits 7
Runtime (s) = 36383.696000
It took over ten hours to fully factor, 2 ^ 66 + 2. I am currently attempting to factor the Thirteenth Fermat number which is 2 ^ (2 ^ 13) + 1 = 2 ^ 8192 + 1. The number has 2,467 decimal digits. I am using 399 algebraic prime numbers, 600 rational prime numbers, and 316 “large prime numbers” (primes between 12,000 and 15,000). I have to find the kernels of a 1316 by 1315 matrix. I am trying the factorization using a maximum of 8192 kernels. I suspect this computation will take about a week on my desktop workstation. There is no guarantee that I will find a non-trivial factor of 2 * (2731 ^ 3) + 2.
Fast and Slow Matrix Multiplication by James Pate Williams, Jr. © January 13, 2024, All Applicable Rights Reserved
Note: For comparison with a paper on matrix operations, we use column major order also known as column major echelon order. Column major order is used in Fortran and row major order is utilized in C computations.
Here is the supposedly slow C source code:
void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
double t = 0;
for (int k = 1; k <= n; k++)
t += a[i][k] * b[k][j];
c[i][j] = t;
}
}
}
And now we present the allegedly fast multiplication code:
void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
double t = b[k][j];
for (int i = 1; i <= n; i++)
c[i][j] += a[i][k] * t;
}
}
}
Finally, we have another algorithm for matrix multiplication:
void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
for (int k = 1; k <= n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
}
We performed the following experiments.
slow runtime in microseconds: 2736
semi runtime in microseconds: 4001
fast runtime in microseconds: 5293
n * n = 10000
equal = 10000
n * n = 10000
equal = 10000
slow runtime in microseconds: 21962
semi runtime in microseconds: 29585
fast runtime in microseconds: 28701
n * n = 40000
equal = 40000
n * n = 40000
equal = 40000
slow runtime in microseconds: 67256
semi runtime in microseconds: 101554
fast runtime in microseconds: 107969
n * n = 90000
equal = 90000
n * n = 90000
equal = 90000
slow runtime in microseconds: 183839
semi runtime in microseconds: 268616
fast runtime in microseconds: 244832
n * n = 160000
equal = 160000
n * n = 160000
equal = 160000
slow runtime in microseconds: 428263
semi runtime in microseconds: 638721
fast runtime in microseconds: 650535
n * n = 250000
equal = 250000
n * n = 250000
equal = 250000
C:\Users\james\source\repos\FastMatrixMultiplication\Debug\FastMatrixMultiplication.exe (process 29552) exited with code 0.
Press any key to close this window . . .
// FastMatrixMultiplication.cpp : This file contains the 'main' function. Program execution begins and ends there.
// https://www-users.york.ac.uk/~mijp1/teaching/grad_HPC_for_MatSci/Lecture4.pdf
// https://stackoverflow.com/questions/25483620/how-to-measure-running-time-of-specific-function-in-c-very-accurate
#include <stdlib.h>
#include <chrono>
#include <iostream>
using namespace std;
typedef chrono::high_resolution_clock Clock;
void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
double t = b[k][j];
for (int i = 1; i <= n; i++)
c[i][j] += a[i][k] * t;
}
}
}
void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
for (int k = 1; k <= n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
}
void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
double t = 0;
for (int k = 1; k <= n; k++)
t += a[i][k] * b[k][j];
c[i][j] = t;
}
}
}
void GenerateMatrix(double** a, int n, int seed)
{
srand(seed);
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
a[j][k] = (double)rand() / RAND_MAX;
}
}
}
int main()
{
for (int n = 100; n <= 500; n += 100)
{
double** a = new double* [n + 1];
double** b = new double* [n + 1];
double** c = new double* [n + 1];
double** d = new double* [n + 1];
double** e = new double* [n + 1];
for (int j = 0; j < n + 1; j++)
{
a[j] = new double[n + 1];
b[j] = new double[n + 1];
c[j] = new double[n + 1];
d[j] = new double[n + 1];
e[j] = new double[n + 1];
}
GenerateMatrix(a, n, 1);
GenerateMatrix(b, n, 2);
auto clock1 = Clock::now();
ColMajorSlowMatMul(a, b, c, n);
auto clock2 = Clock::now();
long long microseconds1 = chrono::duration_cast<chrono::microseconds>
(clock2 - clock1).count();
auto clock3 = Clock::now();
ColMajorSemiMatMul(a, b, d, n);
auto clock4 = Clock::now();
long long microseconds2 = chrono::duration_cast<chrono::microseconds>
(clock4 - clock3).count();
auto clock5 = Clock::now();
ColMajorFastMatMul(a, b, e, n);
auto clock6 = Clock::now();
long long microseconds3 = chrono::duration_cast<chrono::microseconds>
(clock6 - clock5).count();
cout << "slow runtime in microseconds: " << microseconds1 << endl;
cout << "semi runtime in microseconds: " << microseconds2 << endl;
cout << "fast runtime in microseconds: " << microseconds3 << endl;
long long equal = 0;
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (c[j][k] == d[j][k])
equal++;
cout << "n * n = " << n * n << endl;
cout << "equal = " << equal << endl;
equal = 0;
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (c[j][k] == e[j][k])
equal++;
cout << "n * n = " << n * n << endl;
cout << "equal = " << equal << endl;
for (int j = 0; j < n + 1; j++)
{
delete[] a[j];
delete[] b[j];
delete[] c[j];
delete[] d[j];
delete[] e[j];
}
delete[] a;
delete[] b;
delete[] c;
delete[] d;
delete[] e;
}
}
Comparison of Linear Systems Applications in C# and C++ by James Pate Williams, Jr.
Back in 2017 I created a C# application that implemented the direct methods: Cholesky decomposition, Gaussian elimination with partial pivoting, LU decomposition, and simple Gaussian elimination. The classical iterative methods Gauss-Seidel, Jacobi, Successive Overrelaxation, and gradient descent were also implemented along with the modern iterative methods: conjugate gradient descent and Modified Richardson’s method. Recently I translated the C# code to C++. I used the following test matrices: Cauchy, Lehmer, Pascal, and other. Below are some results. As is apparent the C++ runtimes are faster than the C# execution times.
Richardson Method Translated from C Source Code to C# by James Pate Williams, Jr.
The Richardson Method is called before eliminating the system of linear equations.
Added elimination results from a vanilla C program and a C# application.
These results are not in total agreement with H. T. Lau’s results.
Finite Difference Method for Solving Second Order Ordinary Differential Equations by James Pate Williams, Jr.
My reference is Numerical Analysis: An Algorithmic Approach 3rd Edition by S. D. Conte and Carl de Boor Chapter 9.1.
Determinant Calculations: Bareiss Algorithm and Gaussian Elimination by James Pate Williams, Jr.
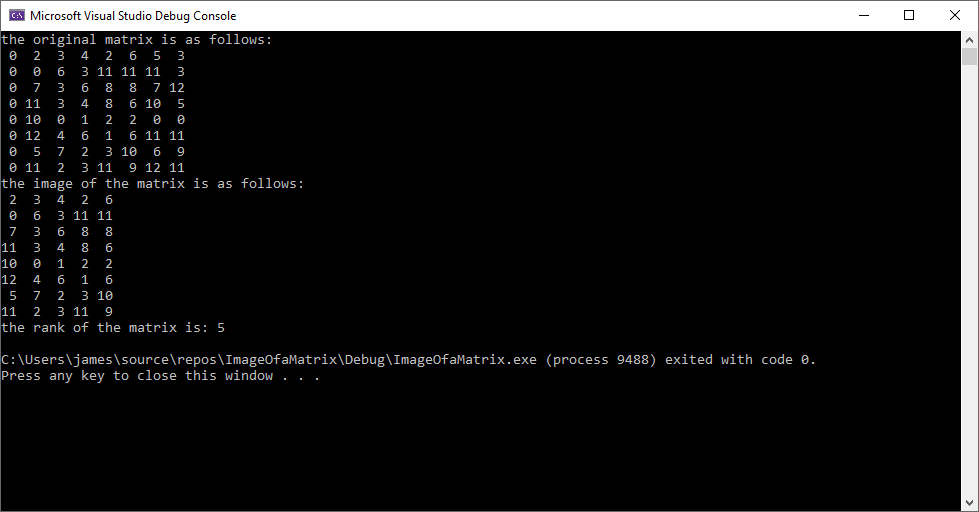
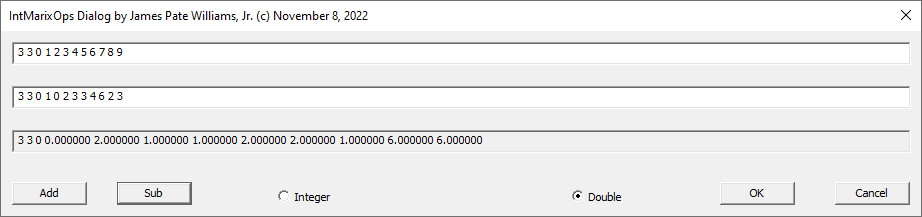
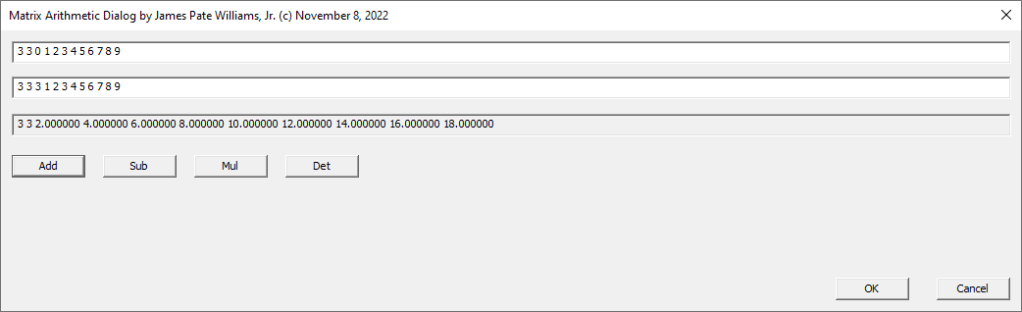
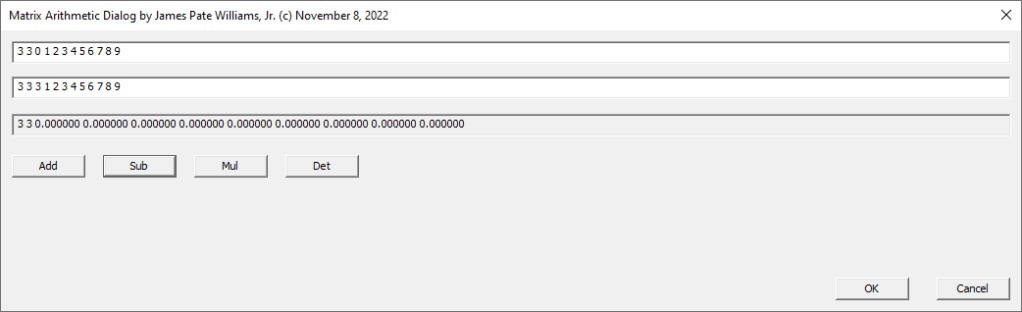
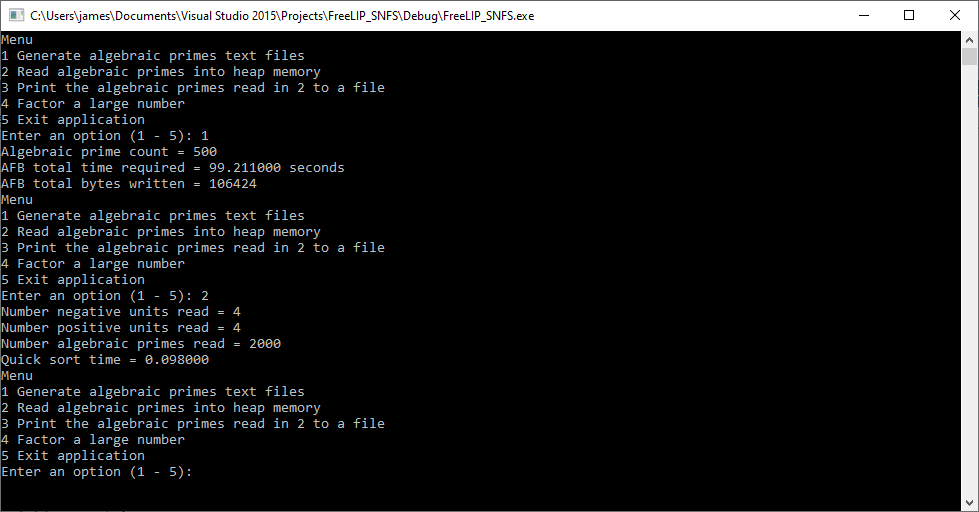
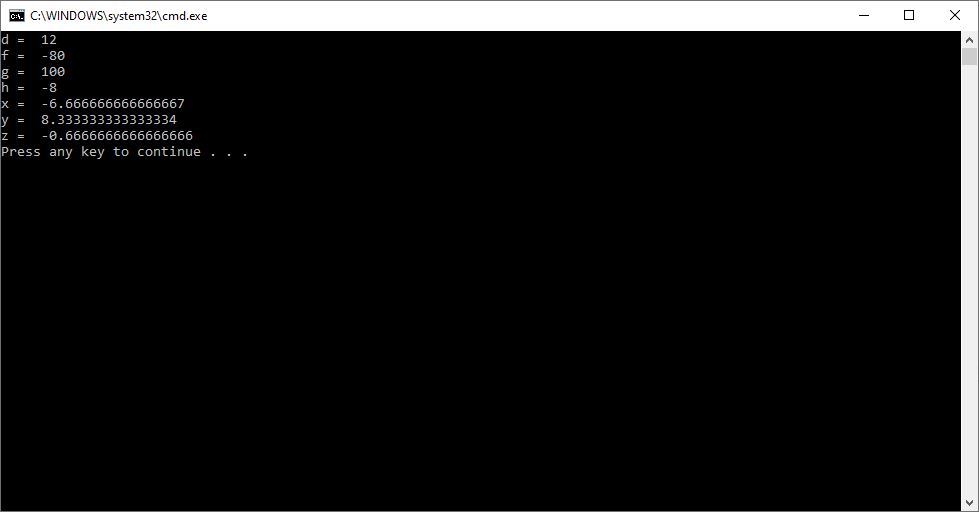
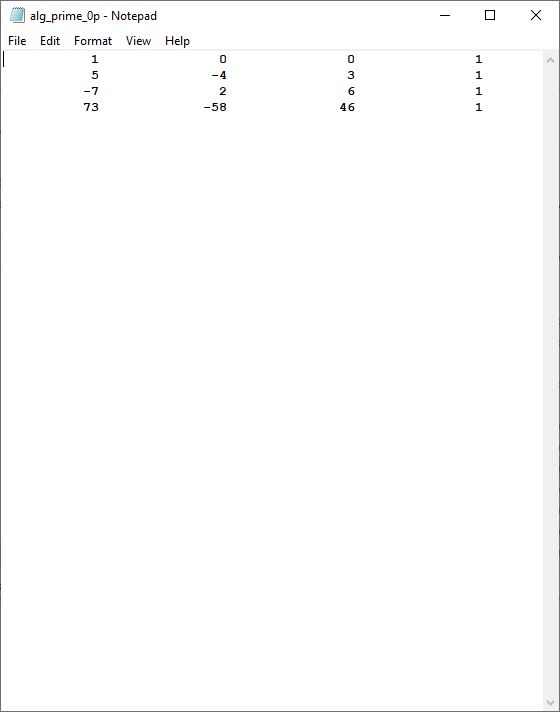Below are three screenshots of two methods of calculating the determinant of a matrix, namely the Bareiss Algorithm and Gaussian Elimination:
using System;
using System.Diagnostics;
using System.Windows.Forms;
namespace MatrixInverseComparison
{
public partial class MainForm : Form
{
public MainForm()
{
InitializeComponent();
}
static private string FormatNumber(double x)
{
string result = string.Empty;
if (x > 0)
result += x.ToString("F5").PadLeft(10);
else
result += x.ToString("F5").PadLeft(10);
return result;
}
private void MultiplyPrintMatricies(
double[,] A, double[,] B, int n)
{
double[,] I = new double[n, n];
textBox1.Text += "Matrix Product:\r\n";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
double sum = 0.0;
for (int k = 0; k < n; k++)
sum += A[i, k] * B[k, j];
I[i, j] = sum;
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
textBox1.Text += FormatNumber(I[i, j]) + " ";
}
textBox1.Text += "\r\n";
}
}
private void PrintMatrix(string title, double[,] A, int n)
{
textBox1.Text += title + "\r\n";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
textBox1.Text += FormatNumber(A[i, j]) + " ";
}
textBox1.Text += "\r\n";
}
}
private void Compute(double[,] MI, int n)
{
double determinantGE = 1;
double[] b = new double[n];
double[] x = new double[n];
double[,] MB1 = new double[n, n];
double[,] MB2 = new double[n, n];
double[,] MG = new double[n, n];
double[,] MS = new double[n, n];
double[,] IG = new double[n, n];
double[,] IS = new double[n, n];
int[] pivot = new int[n];
Stopwatch sw = new();
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
MB1[i, j] = MB2[i, j] = MG[i, j] = MS[i, j] = MI[i, j];
}
PrintMatrix("Initial Matrix: ", MI, n);
sw.Start();
int flag = DirectMethods.Factor(MG, n, pivot);
if (flag != 0)
{
for (int i = 0; i < n; i++)
determinantGE *= MG[i, i];
determinantGE *= flag;
}
sw.Stop();
PrintMatrix("Gaussian Elimination Final:", MG, n);
for (int i = 0; i < n; i++)
b[i] = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
b[j] = 1.0;
DirectMethods.Substitute(MG, b, x, n, pivot);
for (int k = 0; k < n; k++)
IG[k, j] = x[k];
b[j] = 0.0;
}
}
PrintMatrix("Gaussian Elimination Inverse:", IG, n);
textBox1.Text += "Determinant: " +
FormatNumber(determinantGE) + "\r\n";
MultiplyPrintMatricies(IG, MI, n);
textBox1.Text += "Runtime (MS) = " +
sw.ElapsedMilliseconds + "\r\n";
sw.Start();
double determinant1 = BareissAlgorithm.Determinant1(MB1, n);
sw.Stop();
PrintMatrix("Bareiss Algorithm Final 1:", MB1, n);
textBox1.Text += "Determinant: " +
FormatNumber(determinant1) + "\r\n";
textBox1.Text += "Runtime (MS) = " +
sw.ElapsedMilliseconds + "\r\n";
sw.Start();
double determinant2 = BareissAlgorithm.Determinant2(MB2, n);
sw.Stop();
PrintMatrix("Bareiss Algorithm Final 2:", MB2, n);
textBox1.Text += "Determinant: " +
FormatNumber(determinant2) + "\r\n";
textBox1.Text += "Runtime (MS) = " +
sw.ElapsedMilliseconds + "\r\n";
}
private void button1_Click(object sender, EventArgs e)
{
int n = (int)numericUpDown1.Value;
int seed = (int)numericUpDown2.Value;
double[,] A = new double[n, n];
Random random = new Random(seed);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
double q = n * random.NextDouble();
while (q == 0.0)
q = n * random.NextDouble();
A[i, j] = q;
}
}
Compute(A, n);
}
private void button2_Click(object sender, EventArgs e)
{
textBox1.Text = string.Empty;
}
}
}
using System;
namespace MatrixInverseComparison
{
public class DirectMethods
{
// Substitute and Factor translated from FORTRAN 77
// source code found in "Elementary Numerical Analysis:
// An Algorithmic Approach" by S. D. Conte and Carl de
// Boor. Translator: James Pate Williams, Jr. (c)
// August 14 - 17, 2023
static public void Substitute(
double[,] w,
double[] b,
double[] x,
int n,
int[] pivot)
{
double sum;
int i, j, n1 = n - 1;
if (n == 1)
{
x[0] = b[0] / w[0, 0];
return;
}
// forward substitution
x[0] = b[pivot[0]];
for (i = 0; i < n; i++)
{
for (j = 0, sum = 0.0; j < i; j++)
sum += w[i, j] * x[j];
x[i] = b[pivot[i]] - sum;
}
// backward substitution
x[n1] /= w[n1, n1];
for (i = n - 2; i >= 0; i--)
{
for (j = i + 1, sum = 0.0; j < n; j++)
sum += w[i, j] * x[j];
x[i] = (x[i] - sum) / w[i, i];
}
}
// Factor returns +1 if an even number of exchanges
// Factor returns -1 if an odd number of exchanges
// Factor retrurn 0 if matrix is singular
static public int Factor(
double[,] w, int n, int[] pivot)
// returns 0 if matrix is singular
{
double awikod, col_max, ratio, row_max, temp;
double[] d = new double[n];
int flag = 1, i, i_star, j, k;
for (i = 0; i < n; i++)
{
pivot[i] = i;
row_max = 0;
for (j = 0; j < n; j++)
row_max = Math.Max(row_max, Math.Abs(w[i, j]));
if (row_max == 0)
{
flag = 0;
row_max = 1;
}
d[i] = row_max;
}
if (n <= 1)
return flag;
// factorization
for (k = 0; k < n - 1; k++)
{
// determine pivot row the row i_star
col_max = Math.Abs(w[k, k]) / d[k];
i_star = k;
for (i = k + 1; i < n; i++)
{
awikod = Math.Abs(w[i, k]) / d[i];
if (awikod > col_max)
{
col_max = awikod;
i_star = i;
}
}
if (col_max == 0)
flag = 0;
else
{
if (i_star > k)
{
// make k the pivot row by
// interchanging with i_star
flag *= -1;
i = pivot[i_star];
pivot[i_star] = pivot[k];
pivot[k] = i;
temp = d[i_star];
d[i_star] = d[k];
d[k] = temp;
for (j = 0; j < n; j++)
{
temp = w[i_star, j];
w[i_star, j] = w[k, j];
w[k, j] = temp;
}
}
// eliminate x[k]
for (i = k + 1; i < n; i++)
{
w[i, k] /= w[k, k];
ratio = w[i, k];
for (j = k + 1; j < n; j++)
w[i, j] -= ratio * w[k, j];
}
}
}
if (w[n - 1, n - 1] == 0)
flag = 0;
return flag;
}
}
}
namespace MatrixInverseComparison
{
// One implementation is based on https://en.wikipedia.org/wiki/Bareiss_algorithm
// Another perhaps better implementation is found on the following webpage
// https://cs.stackexchange.com/questions/124759/determinant-calculation-bareiss-vs-gauss-algorithm
class BareissAlgorithm
{
static public double Determinant1(double[,] M, int n)
{
double M00;
for (int k = 0; k < n; k++)
{
if (k - 1 == -1)
M00 = 1;
else
M00 = M[k - 1, k - 1];
for (int i = k + 1; i < n; i++)
{
for (int j = k + 1; j < n; j++)
{
M[i, j] = (
M[i, j] * M[k, k] -
M[i, k] * M[k, j]) / M00;
}
}
}
return M[n - 1, n - 1];
}
static public double Determinant2(double[,] A, int dim)
{
if (dim <= 0)
{
return 0;
}
double sign = 1;
for (int k = 0; k < dim - 1; k++)
{
//Pivot - row swap needed
if (A[k, k] == 0)
{
int m;
for (m = k + 1; m < dim; m++)
{
if (A[m, k] != 0)
{
double[] tempRow = new double[dim];
for (int i = 0; i < dim; i++)
tempRow[i] = A[m, i];
for (int i = 0; i < dim; i++)
A[m, i] = A[k, i];
for (int i = 0; i < dim; i++)
A[k, i] = tempRow[i];
sign = -sign;
break;
}
}
//No entries != 0 found in column k -> det = 0
if (m == dim)
{
return 0;
}
}
//Apply formula
for (int i = k + 1; i < dim; i++)
{
for (int j = k + 1; j < dim; j++)
{
A[i, j] = A[k, k] * A[i, j] - A[i, k] * A[k, j];
if (k >= 1)
{
A[i, j] /= A[k - 1, k - 1];
}
}
}
}
return sign * A[dim - 1, dim - 1];
}
}
}
Blast from the Past 1997 Image of a Matrix by James Pate Williams, Jr.
/*
Author: Pate Williams (c) 1997
"Algorithm 2.3.2 (Image of a Matrix). Given an
m by n matrix M = (m[i][i]) with 1 <= i <= m and
1 <= j <= n having coefficients in the field K,
this algorithm outputs a basis of the image of
M, i. e. vector space spanned by the columns of
M." -Henri Cohen- See "A Course in Computational
Algebraic Number Theory" by Henri Cohen pages
58-59. We specialize the code to the field Zp.
*/
#include <stdio.h>
#include <stdlib.h>
long** create_matrix(long m, long n)
{
long i, ** matrix = (long**)calloc(m, sizeof(long*));
if (!matrix) {
fprintf(stderr, "fatal error\ninsufficient memory\n");
fprintf(stderr, "from create_matrix\n");
exit(1);
}
for (i = 0; i < m; i++) {
matrix[i] = (long*)calloc(n, sizeof(long));
if (!matrix[i]) {
fprintf(stderr, "fatal error\ninsufficient memory\n");
fprintf(stderr, "from create_matrix\n");
exit(1);
}
}
return matrix;
}
void delete_matrix(long m, long** matrix)
{
long i;
for (i = 0; i < m; i++) free(matrix[i]);
free(matrix);
}
void Euclid_extended(long a, long b, long* u,
long* v, long* d)
{
long q, t1, t3, v1, v3;
*u = 1, * d = a;
if (b == 0) {
*v = 0;
return;
}
v1 = 0, v3 = b;
#ifdef DEBUG
printf("----------------------------------\n");
printf(" q t3 *u *d t1 v1 v3\n");
printf("----------------------------------\n");
#endif
while (v3 != 0) {
q = *d / v3;
t3 = *d - q * v3;
t1 = *u - q * v1;
*u = v1, * d = v3;
#ifdef DEBUG
printf("%4ld %4ld %4ld ", q, t3, *u);
printf("%4ld %4ld %4ld %4ld\n", *d, t1, v1, v3);
#endif
v1 = t1, v3 = t3;
}
*v = (*d - a * *u) / b;
#ifdef DEBUG
printf("----------------------------------\n");
#endif
}
long inv(long number, long modulus)
{
long d, u, v;
Euclid_extended(number, modulus, &u, &v, &d);
if (d == 1) return u;
return 0;
}
void image(long m, long n, long p,
long** M, long** X, long* r)
{
int found;
long D, i, j, k, s;
long* c = (long*)calloc(m, sizeof(long));
long* d = (long*)calloc(n, sizeof(long));
long** N = create_matrix(m, n);
if (!c || !d) {
fprintf(stderr, "fatal error\ninsufficient memory\n");
fprintf(stderr, "from kernel\n");
exit(1);
}
for (i = 0; i < m; i++) {
c[i] = -1;
for (j = 0; j < n; j++) N[i][j] = M[i][j];
}
*r = 0;
for (k = 0; k < n; k++) {
found = 0, j = 0;
while (!found && j < m) {
found = M[j][k] != 0 && c[j] == -1;
if (!found) j++;
}
if (found) {
D = p - inv(M[j][k], p);
M[j][k] = p - 1;
for (s = k + 1; s < n; s++)
M[j][s] = (D * M[j][s]) % p;
for (i = 0; i < m; i++) {
if (i != j) {
D = M[i][k];
M[i][k] = 0;
for (s = k + 1; s < n; s++) {
M[i][s] = (M[i][s] + D * M[j][s]) % p;
if (M[i][s] < 0) M[i][s] += p;
}
}
}
c[j] = k;
d[k] = j;
}
else {
*r = *r + 1;
d[k] = -1;
}
}
for (j = 0; j < m; j++) {
if (c[j] != -1) {
for (i = 0; i < n; i++) {
if (i < m) X[i][j] = N[i][c[j]];
else X[i][j] = 0;
}
}
}
delete_matrix(m, N);
free(c);
free(d);
}
void print_matrix(long m, long n, long** a)
{
long i, j;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++)
printf("%2ld ", a[i][j]);
printf("\n");
}
}
int main(void)
{
long i, j, m = 8, n = 8, p = 13, r;
long a[8][8] = { {0, 0, 0, 0, 0, 0, 0, 0},
{2, 0, 7, 11, 10, 12, 5, 11},
{3, 6, 3, 3, 0, 4, 7, 2},
{4, 3, 6, 4, 1, 6, 2, 3},
{2, 11, 8, 8, 2, 1, 3, 11},
{6, 11, 8, 6, 2, 6, 10, 9},
{5, 11, 7, 10, 0, 11, 6, 12},
{3, 3, 12, 5, 0, 11, 9, 11} };
long** M = create_matrix(m, n);
long** X = create_matrix(n, n);
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
M[i][j] = a[j][i];
printf("the original matrix is as follows:\n");
print_matrix(m, n, M);
image(m, n, p, M, X, &r);
printf("the image of the matrix is as follows:\n");
print_matrix(n, n - r, X);
printf("the rank of the matrix is: %ld\n", n - r);
delete_matrix(m, M);
delete_matrix(n, X);
return 0;
}
First Blast from the Past (1997) Computing the Inverse Image of a Matrix by James Pate Williams, Jr.
/*
Author: Pate Williams (c) 1997
"Algorithm 2.3.5 (Inverse Image Matrix). Let M be
an m by n matrix and V be an m by r matrix, where
n <= m. This algorithm either outputs a message
saying that some column vector of V is not in the
image of M, or outputs an n by r matrix X such
that V = MX." -Henri Cohen- See "A Course in Com-
putational Algebraic Number Theory" by Henri
Cohen pages 60-61. We specialize to the field Q.
*/
#include <stdio.h>
#include <stdlib.h>
double** create_matrix(long m, long n)
{
double** matrix = (double**)calloc(m, sizeof(double*));
long i;
if (!matrix) {
fprintf(stderr, "fatal error\ninsufficient memory\n");
fprintf(stderr, "from create_matrix\n");
exit(1);
}
for (i = 0; i < m; i++) {
matrix[i] = (double*)calloc(n, sizeof(double));
if (!matrix[i]) {
fprintf(stderr, "fatal error\ninsufficient memory\n");
fprintf(stderr, "from create_matrix\n");
exit(1);
}
}
return matrix;
}
void delete_matrix(long m, double** matrix)
{
long i;
for (i = 0; i < m; i++) free(matrix[i]);
free(matrix);
}
void inverse_image_matrix(long m, long n, long r,
double** M, double** V,
double** X)
{
double ck, d, sum, t;
double** B = create_matrix(m, r);
int found;
long i, j, k, l;
for (i = 0; i < m; i++)
for (j = 0; j < r; j++)
B[i][j] = V[i][j];
for (j = 0; j < n; j++) {
found = 0, i = j;
while (!found && i < m) {
found = M[i][j] != 0;
if (!found) i++;
}
if (!found) {
fprintf(stderr, "fatal error\nnot linearly independent\n");
fprintf(stderr, "from inverse_image_matrix\n");
exit(1);
}
if (i > j) {
for (l = 0; l < n; l++)
t = M[i][l], M[i][l] = M[j][l], M[j][l] = t;
for (l = 0; l < r; l++)
t = B[i][l], B[i][l] = B[j][l], B[j][l] = t;
}
d = 1.0 / M[j][j];
for (k = j + 1; k < m; k++) {
ck = d * M[k][j];
for (l = j + 1; l < n; l++)
M[k][l] -= ck * M[j][l];
for (l = 0; l < r; l++)
B[k][l] -= ck * B[j][l];
}
}
for (i = n - 1; i >= 0; i--) {
for (k = 0; k < r; k++) {
sum = 0;
for (j = i + 1; j < n; j++)
sum += M[i][j] * X[j][k];
X[i][k] = (B[i][k] - sum) / M[i][i];
}
}
for (k = n + 1; k < m; k++) {
for (j = 0; j < r; j++) {
sum = 0;
for (i = 0; i < n; i++)
sum += M[k][i] * X[i][j];
if (sum != B[k][j]) {
fprintf(stderr, "fatal error\ncolumn not in image\n");
fprintf(stderr, "from inverse_image_matrix\n");
exit(1);
}
}
}
delete_matrix(m, B);
}
void matrix_multiply(long m, long n, long r,
double** a, double** b,
double** c)
/* c = a * b */
{
double sum;
long i, j, k;
for (i = 0; i < m; i++) {
for (j = 0; j < r; j++) {
sum = 0.0;
for (k = 0; k < n; k++)
sum += a[i][k] * b[k][j];
c[i][j] = sum;
}
}
}
void print_matrix(long m, long n, double** a)
{
long i, j;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++)
printf("%+10.6lf ", a[i][j]);
printf("\n");
}
}
int main(void)
{
long i, j, m = 4, n = 4, r = 4;
double** c = create_matrix(m, n);
double** M = create_matrix(m, n);
double** V = create_matrix(m, r);
double** X = create_matrix(n, r);
for (i = 0; i < m; i++) {
c[i][i] = M[i][i] = 2.0;
if (i > 0)
c[i][i - 1] = M[i][i - 1] = -1.0;
if (i < m - 1)
c[i][i + 1] = M[i][i + 1] = -1.0;
}
for (i = 0; i < m; i++)
for (j = 0; j < r; j++)
V[i][j] = i + j + 1;
printf("M is as follows:\n");
print_matrix(m, n, M);
printf("V is as follows:\n");
print_matrix(m, r, V);
inverse_image_matrix(m, n, r, M, V, X);
printf("X is as follows:\n");
print_matrix(n, r, X);
matrix_multiply(m, n, r, c, X, M);
printf("MX is as follows:\n");
print_matrix(m, r, M);
delete_matrix(m, c);
delete_matrix(m, M);
delete_matrix(m, V);
delete_matrix(n, X);
return 0;
}
