The sieve of Eratosthenes handles primes up to an upper bound of 100,000,000. The number of primes is 5,761,455. Below are a few examples runs of the app. I have also created C source code for trial division and other factoring algorithms that use Professor Emeritus Arjen K. Lenstra’s Free Large Integer Package also known as lip.
Enter n (<= 18) below:
5
Enter k (<= 18) below:
0
1 1
Enter n (<= 18) below:
5
Enter k (<= 18) below:
1
5 5
Enter n (<= 18) below:
5
Enter k (<= 18) below:
2
10 10
Enter n (<= 18) below:
0
Enter n (<= 18) below:
0
Pascal's Triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
1 17 136 680 2380 6188 12376 19448 24310 24310 19448 12376 6188 2380 680 136 17 1
1 18 153 816 3060 8568 18564 31824 43758 48620 43758 31824 18564 8568 3060 816 153 18 1
C:\Users\james\source\repos\BinomialCoefficeint\Debug\BinomialCoefficeint.exe (process 40028) exited with code 0.
Press any key to close this window . . .
// BinomialCoefficient.c (c) Monday, June 24, 2024
// by James Pate Williams, Jr. BA, BS, MSwE, PhD
#include <stdio.h>
#include <stdlib.h>
typedef long long ll;
ll** Binomial(ll n)
{
ll** C = (ll**)calloc(n + 1, sizeof(ll*));
if (C == NULL)
exit(-1);
for (int i = 0; i < n + 1; i++)
{
C[i] = (ll*)calloc(n + 1, sizeof(ll));
if (C[i] == NULL)
exit(-1);
}
if (n >= 0)
{
C[0][0] = 1;
}
if (n >= 1)
{
C[1][0] = 1;
C[1][1] = 1;
}
if (n >= 2)
{
for (int i = 2; i <= n; i++)
{
for (int j = 2; j <= n; j++)
{
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
return C;
}
ll Factorial(ll n)
{
ll fact = 1;
if (n > 1)
{
for (int i = 2; i <= n; i++)
fact = i * fact;
}
return fact;
}
ll BC(ll n, ll k)
{
return Factorial(n) / (Factorial(n - k) * Factorial(k));
}
int main()
{
int i = 0, j = 0;
ll** C = Binomial(20);
while (1)
{
char buffer[256] = { '\0' };
printf_s("Enter n (<= 18) below:\n");
scanf_s("%s", buffer, sizeof(buffer));
printf_s("\n");
ll n = atoll(buffer);
if (n == 0)
break;
printf_s("Enter k (<= 18) below:\n");
scanf_s("%s", buffer, sizeof(buffer));
printf_s("\n");
ll k = atoll(buffer);
printf_s("%lld\t%lld\n\n", C[n + 2][k + 2], BC(n, k));
}
printf_s("Pascal's Triangle:\n\n");
for (i = 2; i <= 20; i++)
{
for (j = 2; j <= 20; j++)
if (C[i][j] != 0)
printf_s("%5lld ", C[i][j]);
printf_s("\n");
}
for (i = 0; i <= 20; i++)
free(C[i]);
free(C);
}
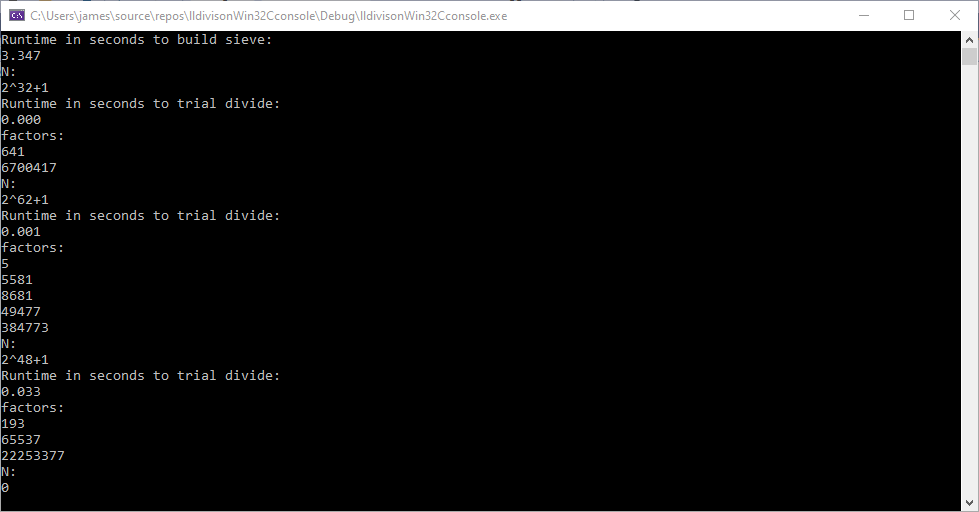
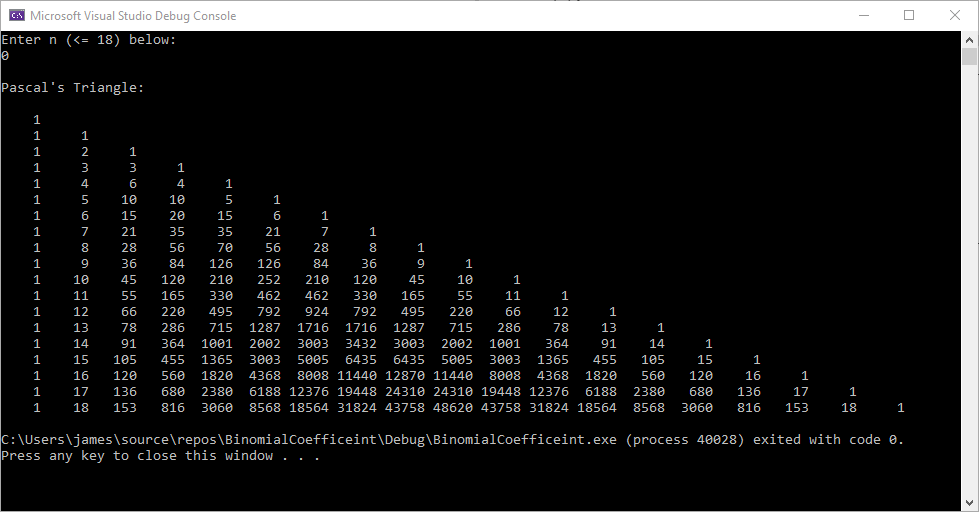
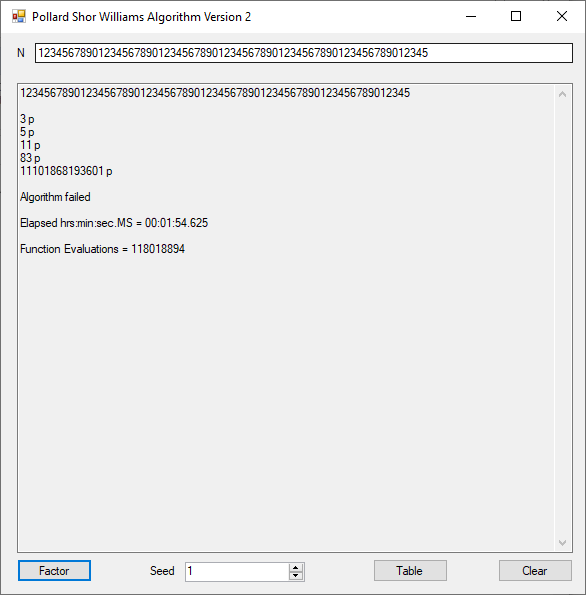
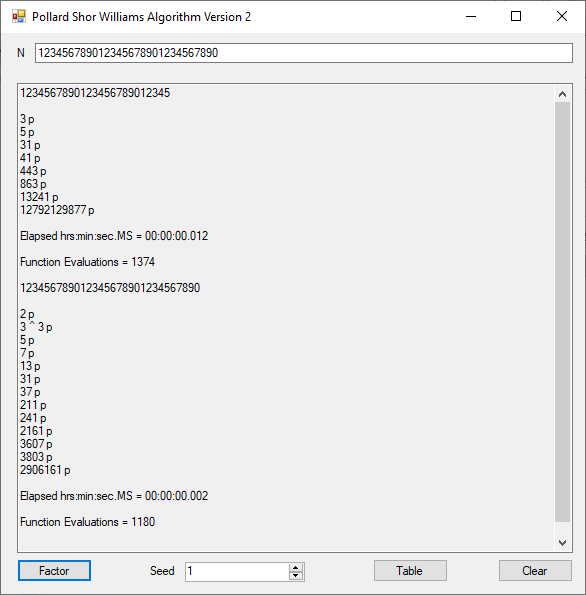
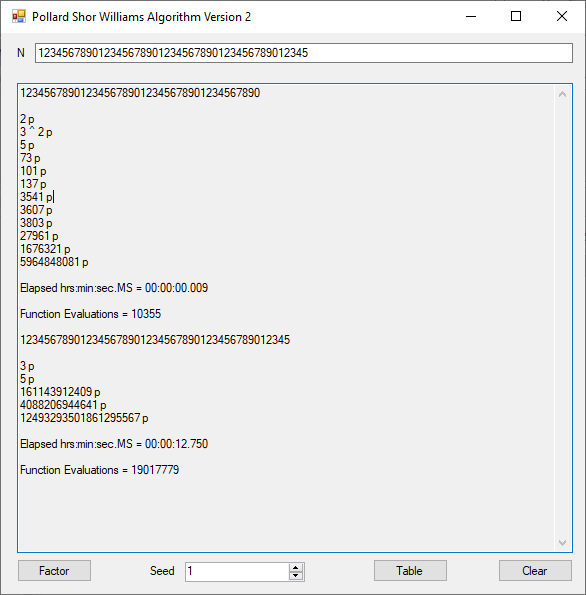
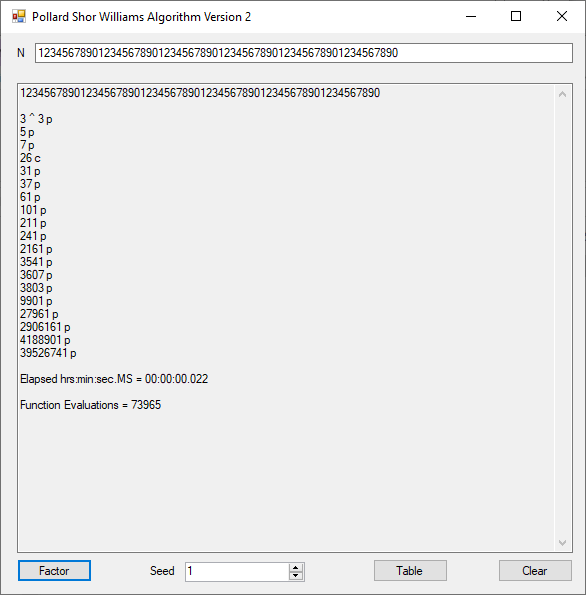
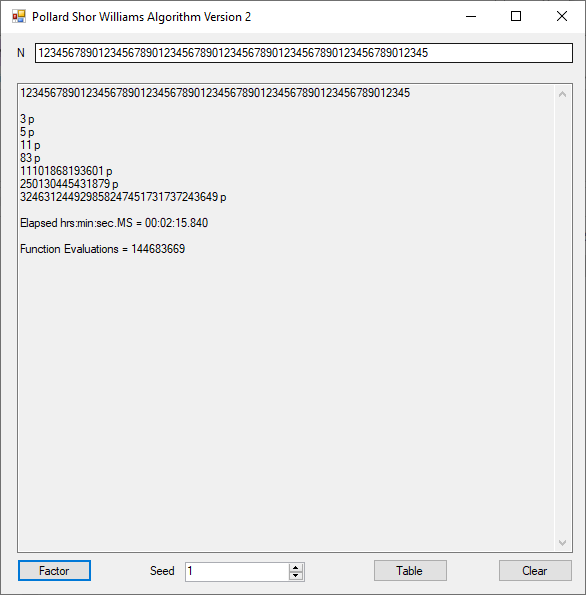
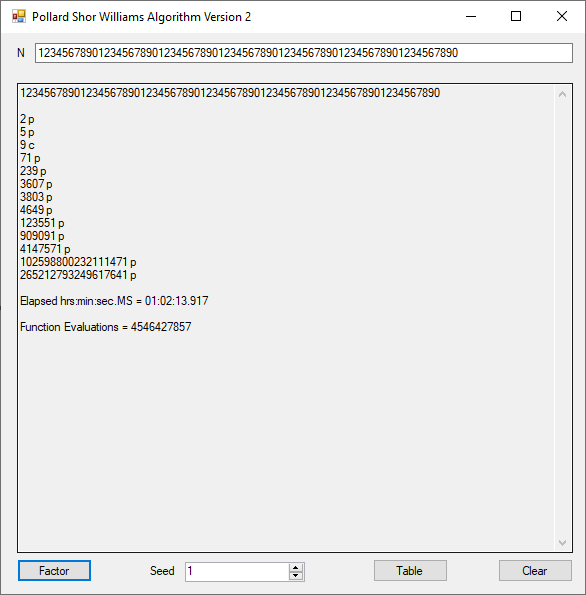
The object of this C Win32 application is to find a multiple of 9 with its digits summing to a multiple of 9 also. The first column below is a multiple of 9 whose digits sum to 9 also. The second column is the sum of digits found in the column one number. The last column is the first column divided by 9.
Enter PRNG seed:
1
Enter number of bits (4 to 16):
4
9 9 1
Enter number of bits (4 to 16):
5
27 9 3
Enter number of bits (4 to 16):
6
45 9 5
Enter number of bits (4 to 16):
7
117 9 13
Enter number of bits (4 to 16):
8
252 9 28
Enter number of bits (4 to 16):
0
C:\Users\james\source\repos\CProductOf9Console\Debug\CProductOf9Console.exe (process 23280) exited with code 0.
Press any key to close this window . . .
Enter PRNG seed:
1
Enter number of bits (4 to 16):
9
369 18 41
Enter number of bits (4 to 16):
10
846 18 94
Enter number of bits (4 to 16):
11
1080 9 120
Enter number of bits (4 to 16):
12
3015 9 335
Enter number of bits (4 to 16):
13
5040 9 560
Enter number of bits (4 to 16):
14
10350 9 1150
Enter number of bits (4 to 16):
15
30870 18 3430
Enter number of bits (4 to 16):
16
57798 36 6422
Enter number of bits (4 to 16):
0
// CProductOf9Console.c (c) Sunday, June 23, 2024
// by James Pate Williams, Jr., BA, BS, MSwE, PhD
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
char nextStr[256], numbStr[256];
void ConvertToString(int number, int radix)
{
int i = 0;
while (number > 0)
{
nextStr[i++] = (char)(number % radix + '0');
number /= radix;
}
nextStr[i++] = '\0';
_strrev(nextStr);
}
int Sum(int next)
{
long sum = 0;
ConvertToString(next, 10);
for (int i = 0; i < (int)strlen(nextStr); i++)
sum += (long)nextStr[i] - '0';
if (sum % 9 == 0 && sum != 0)
return sum;
return -1;
}
long GetNext(int numBits, int* next)
{
long hi = 0, lo = 0, nine = 0;
nextStr[0] = '\0';
numbStr[0] = '\0';
if (numBits == 4)
{
while (1)
{
*next = 9 * (long)(rand() % 16);
if (*next != 0 && *next >= 8 && *next < 16)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 5)
{
while (1)
{
*next = 9 * (long)(rand() % 32);
if (*next >= 16 && *next < 32)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 6)
{
while (1)
{
*next = 9 * (long)(rand() % 64);
if (*next >= 32 && *next < 64)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 7)
{
while (1)
{
*next = 9 * (long)(rand() % 128);
if (*next >= 64 && *next < 128)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 8)
{
while (1)
{
*next = 9 * (long)(rand() % 256);
if (*next >= 128 && *next < 256)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 9)
{
while (1)
{
*next = 9 * (long)(rand() % 512);
if (*next >= 256 && *next < 512)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 10)
{
while (1)
{
*next = 9 * (long)(rand() % 1024);
if (*next >= 512 && *next < 1024)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 11)
{
while (1)
{
*next = 9 * (long)(rand() % 2048);
if (*next >= 1024 && *next < 2048)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 12)
{
while (1)
{
*next = 9 * (long)(rand() % 4096);
if (*next >= 2048 && *next < 4096)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 13)
{
while (1)
{
*next = 9 * (long)(rand() % 8192);
if (*next >= 4096 && *next < 8192)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 14)
{
while (1)
{
*next = 9 * (long)(rand() % 16384);
if (*next >= 8192 && *next < 16384)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 15)
{
while (1)
{
*next = 9 * (long)(rand() % 32768);
if (*next >= 16384 && *next < 32768)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
else if (numBits == 16)
{
while (1)
{
*next = 9 * (long)(rand() % 65536);
if (*next >= 32768 && *next < 65536)
{
nine = Sum(*next);
if (nine % 9 == 0)
return nine;
}
}
}
return -1;
}
int main()
{
char buffer[256] = { '\0' };
long seed = 0;
printf_s("Enter PRNG seed:\n");
scanf_s("%s", buffer, sizeof(buffer));
seed = atol(buffer);
srand((unsigned int)seed);
while (1)
{
int next = 0, nine = 0, numberBits = 0;
printf_s("Enter number of bits (4 to 16):\n");
scanf_s("%s", buffer, sizeof(buffer));
numberBits = atol(buffer);
if (numberBits == 0)
break;
if (numberBits < 4 || numberBits > 16)
{
printf_s("illegal number of bits must >= 4 and <= 16\n");
continue;
}
nine = GetNext(numberBits, &next);
if (nine == -1)
{
printf_s("illegal result, try again\n");
continue;
}
printf_s("%5ld\t%5ld\t%5ld\n", next, nine, next / 9);
}
return 0;
}
FreeLIP is a free large integer package solely created by Professor Emeritus Arjen K. Lenstra of the Number Field Sieve fame. He developed FreeLIP while he was an employee of AT&T – Lucent in the late 1980s. His copyright notice in the header file, lip.h, states copyright from 1989 to 1997. I have been using this excellent number theoretical package since the late 1990s. See the paper by Donald E. Knuth and Thomas J. Buckholtz for the formula for Tangent Numbers. I can’t remember where I got the Euler Numbers recurrence relation. I wrote a C# application in 2015 for computing Euler Numbers. The code below is in the vanilla C computer language. Excellent resources for the Euler and tangent numbers also known as zag numbers are:
This application implements the algorithm described in the paper at the URL http://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf. I replaced Step 1 of the algorithm with the Miller-Rabin probabilistic primality test. If that test shows that the number is composite, I return the value COMPOSITE. This algorithm is much easier to implement and understand that Wieb Bosmer’s Primality Proving with Cyclotomy also known as the Jacobi sums primality test. As a test we determine that the following Mersenne numbers are prime: M_1279, M_2203, M_2281, M_3217, and M_4253 where M_n = 2 ^ n – 1, and the primes have 386, 664, 687, 969, and 1281 decimal digits, respectively. M_1279 was first proven prime by Raphael M. Robinson on June 25, 1952, using the Lucas-Lehmer test on a SWAC computer. The same author found that M_2203 was prime on October 7, 1952, and M_2281 was prime on October 9, 1952, using the same method and computer. Hans Riesel determined that M_3217 was prime on September 8, 1957, using the Lucas-Lehmer test on a BESK computer. M_4253 was proven prime on November 3, 1961 by Alexander Hurwitz using the Lucas-Lehmer test on an IBM 7090 mainframe computer. See http://www.mersenne.org/primes/ for many more Mersenne primes. All of the computations illustrated below were performed on a late November 2015 Dell XPS 8900 computer with 16 GB RAM Intel(R) Core(TM) i7-6700K CPU @ 4.00 GHz running Windows 10 Pro. The .Net framework is .Net 4.5.2. This is a multitasking version of the original BigInteger variant of the application. Someone with a quad core CPU with 8 virtual processors can try NumberTasks = 8 to see if that speeds up this application more or less. I usually try to limit the number of tasks to actual number of cores.
I am working on a factorization of the Thirteenth Fermat number which is 2 ^ 8192 + 1 and is 2,467 decimal digits in length. I am using Pollard’s factoring with cubic integers on the number (2 ^ 2731) ^ 3 + 2. I am also utilizing a homegrown variant of the venerable Pollard and Brent rho method and Arjen K. Lenstra’s Free LIP Elliptic Curve Method. I can factor the seventh Fermat number 2 ^ 128 + 1 in five to thirty minutes using my C# code. The factoring with cubic integers code is in C and uses Free-LIP.
Fermat factoring status (prothsearch.com)
The following is a run of Lenstra’s ECM algorithm:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^8192+1
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 1
2710954639361 p # digits 13
3603109844542291969 p # digits 19
Runtime (s) = 17015.344000
I aborted the previous computation due to the fact I was curious about the number of prime factors that could be found on personal computer. I will try a lot more calculation time in a future run. My homegrown application is able to at least find the first factor of Fermat Number 13.
All of the following computations were performed on a late 2015 Dell XPS 8900 personal computer with a 64-bit Intel Core I7 processor @ 4.0GHz with 16GB of DDR2 RAM.
Factorization of Six Fibonacci Sequence Numbers:
Fibonacci 500
# digits 105
5 ^ 2 p # digits 1
15 c # digits 2
101 p # digits 3
401 p # digits 3
1661 c # digits 4
3001 p # digits 4
10291 c # digits 5
570601 p # digits 6
112128001 p # digits 9
1353439001 p # digits 10
28143378001 p # digits 11
5465167948001 p # digits 13
84817574770589638001 p # digits 20
158414167964045700001 p # digits 21
Runtime (s) = 1.206000
Fibonacci 505
# digits 106
5 p # digits 1
743519377 p # digits 9
44614641121 p # digits 11
770857978613 p # digits 12
960700389041 p # digits 12
12588421794766514566269164716286291055826556238643852856601641 p # digits 62
Runtime (s) = 1.959000
Fibonacci 510
# digits 107
2 ^ 3 p # digits 1
11 p # digits 2
61 p # digits 2
1021 p # digits 4
1597 p # digits 4
3469 p # digits 4
3571 p # digits 4
9521 p # digits 4
53551 p # digits 5
95881 p # digits 5
142445 c # digits 6
1158551 p # digits 7
3415914041 p # digits 10
20778644396941 p # digits 14
20862774425341 p # digits 14
81358225616651 c # digits 14
162716451241291 p # digits 15
Runtime (s) = 2.682000
Fibonacci 515
# digits 108
5 p # digits 1
519121 p # digits 6
5644193 p # digits 7
512119709 p # digits 9
84388938382141 p # digits 14
300367026458796424297447559250634818495937628065437243817852436228914621 p # digits 72
Runtime (s) = 7.861000
Fibonacci 520
# digits 109
131 p # digits 3
451 c # digits 3
521 p # digits 3
2081 p # digits 4
2161 p # digits 4
3121 p # digits 4
24571 p # digits 5
90481 p # digits 5
2519895 c # digits 7
21183761 p # digits 8
57089761 p # digits 8
102193207 p # digits 9
1932300241 p # digits 10
14736206161 p # digits 11
5836312049326721 p # digits 16
42426476041450801 p # digits 17
Runtime (s) = 5.155000
Fibonacci 525
# digits 110
2 p # digits 1
5 p # digits 1
421 p # digits 3
701 p # digits 3
3001 p # digits 4
3965 c # digits 4
4201 p # digits 4
141961 p # digits 6
2553601 p # digits 7
230686501 p # digits 9
8288823481 p # digits 10
82061511001 p # digits 11
19072991752501 c # digits 14
8481116649425701 p # digits 16
17231203730201189308301 p # digits 23
Runtime (s) = 2.026000
Factorization of Six Lucas Sequence Numbers
Lucas 340
113709744839525149336680459091826532688903186653162057995534262332121127
# digits 72
7 p # digits 1
2161 p # digits 4
5441 p # digits 4
897601 p # digits 6
23230657239121 p # digits 14
17276792316211992881 p # digits 20
3834936832404134644974961 p # digits 25
Runtime (s) = 109.103000
Lucas 345
# digits 73
2 ^ 2 p # digits 1
31 p # digits 2
461 p # digits 3
1151 p # digits 4
1529 c # digits 4
324301 p # digits 6
686551 p # digits 6
1485571 p # digits 7
4641631 p # digits 7
19965899801 c # digits 11
117169733521 p # digits 12
3490125311294161 p # digits 16
Runtime (s) = 0.032000
Lucas 350
13985374084677485786380981408251904922622980674054858121032362563653278123
# digits 74
3 p # digits 1
401 p # digits 3
2801 p # digits 4
11521 c # digits 5
28001 p # digits 5
570601 p # digits 6
12317523121 p # digits 11
248773766357061401 p # digits 18
7358192362316341243805801 p # digits 25
Runtime (s) = 21.047000
Lucas 355
69362907070206748494476200566565775354902428015845969798000696945226974645
# digits 74
5 p # digits 1
4261 p # digits 4
6673 p # digits 4
75309701 p # digits 8
309273161 p # digits 9
46165371073 p # digits 11
9207609261398081 p # digits 16
49279722643391864192801 p # digits 23
Runtime (s) = 40.726000
Lucas 360
769246427201094785080787978422393713094534885688979999504447628313150135520
# digits 75
2 ^ 5 p # digits 1
3 ^ 2 p # digits 1
23 p # digits 2
41 p # digits 2
105 c # digits 3
107 p # digits 3
241 p # digits 3
2161 p # digits 4
2521 p # digits 4
3439 c # digits 4
8641 p # digits 4
20641 p # digits 5
103681 p # digits 6
109441 p # digits 6
191306797 c # digits 9
10783342081 p # digits 11
13373763765986881 p # digits 17
Runtime (s) = 0.032000
Lucas 365
19076060504701386559675231910437330047906343529583769121365013189782992678011
# digits 77
11 p # digits 2
151549 p # digits 6
514651 p # digits 6
7015301 p # digits 7
8942501 p # digits 7
9157663121 p # digits 10
11899937029 p # digits 11
3252336525249736694804553589211 p # digits 31
The following two numbers were first factorized by J. M. Pollard on an 8-bit Phillips P2012 personal computer with 64 KB RAM and two 640 KB disc drives. The times required by Pollard were 41 and 47 hours.
2^144-3
22300745198530623141535718272648361505980413
# digits 44
492729991333 p # digits 12
45259565260477899162010980272761 p # digits 32
Runtime (s) = 0.086000
2^153+3
11417981541647679048466287755595961091061972995
# digits 47
5 p # digits 1
11 p # digits 2
600696432006490087537 p # digits 21
345598297796034189382757 p # digits 24
Runtime (s) = 0.676000
Partial factorization of the Twelfth Fermat Number 2^4096+1
# digits 1234
114689 p # digits 6
26017793 p # digits 8
63766529 p # digits 8
190274191361 p # digits 12
Runtime (s) = 1532.878000
This factoring algorithm is based on Pollard’s rho, Shor’s classical, and my modification of the two preceding methods.
Numerical Explorations 