Polyalphabetic Cipher – Numerical Explorations

Another Matrix Cipher by James Pate Williams, Jr. BA, BS, MSwE, PhD

This is perhaps an improvement on the matrix cipher of a previous blog post of mine. In that post I introduced a matrix cipher whose keys were generated by selection of a seed such that 1 <= seed <= 2147483647, a number N such that 2 <= N <= 1000, and plaintext of length n such that 1 <= n <= N -1.

This matrix cipher relies on the ANSI X9.17 pseudorandom number generator (PRNG) of 5.11 Algorithm of the Handbook of Applied Cryptography by Alfred J. Menezes, et al. The PRNG uses triple-DES with a potential 168-bit (56 * 3 = 168) key space using E-D-E (Encryption key 1 – Decryption key 2 – Encryption key 3). Also, a 64-bit date related number and a 64-bit random seed are needed to initialize the PRNG.

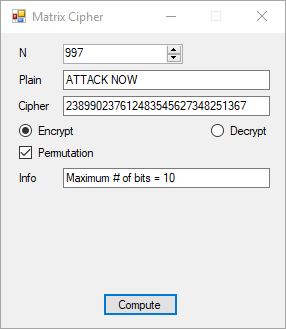
The key space for the algorithm is (168 + 128) bits which is 296 bits. Here is the encryption and decryption of the ASCII ten characters string “ATTACK NOW”.

New Matrix Cipher 0

New Matrix Cipher 1

New Matrix Cipher 2

New Matrix Cipher 3

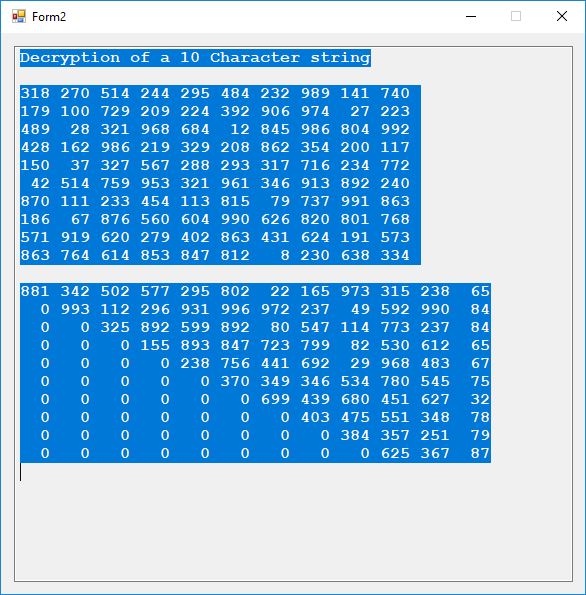
New Matrix Cipher 4

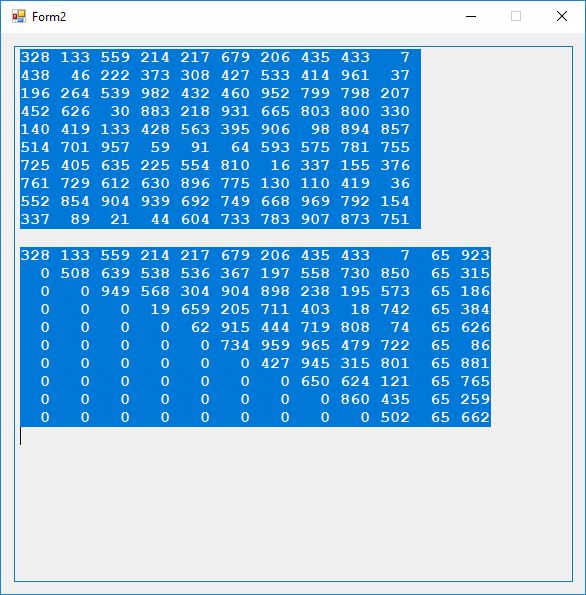
The first step in the cryptanalysis of this cipher would be to determine the modulus of the matrix and vector calculations N. I don’t know how many ciphertexts would be necessary to perform this task. From the preceding known ciphertext we find that N is at least 991. From traffic analysis we may have determined that the maximum value of N is 1000. That means would we only need to try 10 values of N.

A Matrix Cipher by James Pate Williams, Jr., BA, BS, MSwE, PhD

Suppose you have a n vector of ASCII encoded characters, arbitrarily choose 1 <= n <= 1000. Choose a modulus N such that 128 <= N <= 1000. Also choose a pseudo-random number seed 1 <= s <= 2147483647. Next find a random n x n matrix that is invertible by Gaussian elimination over the integer field consisting of N elements. Suppose this matrix is M and its tridiagonal form is M’. Now suppose the plaintext is the n vector P and the ciphertext is the n vector C then we have for encryption:

C = M’P

Further assume the inverse of M’ is N’. For decryption we use the equation:

P = N’C

Where

M’N’ = N’M’ = I

Such that I is the n x n identity matrix.

This cipher is related to the classic Hill Cipher. This cipher is polyalphabetic. We show the results of one encryption and decryption using 10 ASCII ‘A’ characters, N = 999, and s = 1. As you can see each occurrence of the letter ‘A’ which is encoded as the decimal number 65 leads to different integer in the range 0 to 998 which has a maximum of 10 bits. The key consists of the 100 integers in the original 10 x 10 matrix. The application was implemented in C# using a Gaussian elimination over a number field algorithm from Henri Cohen’s A Course in Computational Algebraic Number Theory.

Matrix Cipher 0

Matrix Cipher 1

Matrix Cipher 2

Machine Cryptanalysis of Basic Cryptosystems by James Pate Williams, Jr. BA, BS, MSwE, PhD

In Winter and Spring 2018 I wrote a simple C# computer program to perform machine cryptanalysis of the following basic (elementary and easily breakable) cryptosystems:

Affine Cipher Operating on Monographs and Digraphs
Matrix Cipher
Mono-alphabetic Cipher
n-Rotor with Shifting Polyalphabetic Cipher

The key ingredient in this program is a relatively extensive English language dictionary.

This slideshow requires JavaScript.