Category: Schrödinger Equation
Blog Entry © Tuesday, March 25, 2025, by James Pate Williams, Jr. Hydrogen Radial Wavefunctions and Related Functions
Blog Entry, Thursday, March 20, 2025, Another Helium Variational Calculation by James Pate Williams, Jr.
Live Person-to-Person Tutoring
Blog Entry © Saturday, November 30, 2024, by James Pate Williams, Jr. Partial Solution of the Schrödinger Equation for Hydrogen in Parabolic Coordinates
Blog Entry (c) Wednesday, November 6, 2024, by James Pate Williams, Jr. Small Angular Momentum Quantum Numbers Gaunt Coefficients
// GauntCoefficients.cpp (c) Monday, November 4, 2024
// by James Pate Williams, Jr., BA, BS, MSWE, PhD
// Computes the Gaunt angular momentum coefficients
// Also the Wigner-3j symbols are calculated
// https://en.wikipedia.org/wiki/3-j_symbol
// https://doc.sagemath.org/html/en/reference/functions/sage/functions/wigner.html#
// https://www.geeksforgeeks.org/factorial-large-number/
#include <iostream>
using namespace std;
typedef long double real;
real pi;
// iterative n-factorial function
real Factorial(int n)
{
real factorial = 1;
for (int i = 2; i <= n; i++)
factorial *= i;
if (n < 0)
factorial = 0;
return factorial;
}
real Delta(int lt, int rt)
{
return lt == rt ? 1.0 : 0.0;
}
real Wigner3j(
int j1, int j2, int j3,
int m1, int m2, int m3)
{
real delta = Delta(m1 + m2 + m3, 0) *
powl(-1.0, j1 - j2 - m3);
real fact1 = Factorial(j1 + j2 - j3);
real fact2 = Factorial(j1 - j2 + j3);
real fact3 = Factorial(-j1 + j2 + j3);
real denom = Factorial(j1 + j2 + j3 + 1);
real numer = delta * sqrt(
fact1 * fact2 * fact3 / denom);
real fact4 = Factorial(j1 - m1);
real fact5 = Factorial(j1 + m1);
real fact6 = Factorial(j2 - m2);
real fact7 = Factorial(j2 + m2);
real fact8 = Factorial(j3 - m3);
real fact9 = Factorial(j3 + m3);
real sqrt1 = sqrtl(
fact4 * fact5 * fact6 * fact7 * fact8 * fact9);
real sumK = 0;
int K = (int)fmaxl(0, fmaxl((real)j2 - j3 - m1,
(real)j1 - j3 + m2));
int N = (int)fminl((real)j1 + j2 - j3,
fminl((real)j1 - m1, (real)j2 + m2));
for (int k = K; k <= N; k++)
{
real f0 = Factorial(k);
real f1 = Factorial(j1 + j2 - j3 - k);
real f2 = Factorial(j1 - m1 - k);
real f3 = Factorial(j2 + m2 - k);
real f4 = Factorial(j3 - j2 + m1 + k);
real f5 = Factorial(j3 - j1 - m2 + k);
sumK += powl(-1.0, k) / (f0 * f1 * f2 * f3 * f4 * f5);
}
return numer * sqrt1 * sumK;
}
real GauntCoefficient(
int l1, int l2, int l3, int m1, int m2, int m3)
{
real factor = sqrtl(
(2.0 * l1 + 1.0) *
(2.0 * l2 + 1.0) *
(2.0 * l3 + 1.0) /
(4.0 * pi));
real wigner1 = Wigner3j(l1, l2, l3, 0, 0, 0);
real wigner2 = Wigner3j(l1, l2, l3, m1, m2, m3);
return factor * wigner1 * wigner2;
}
int main()
{
pi = 4.0 * atanl(1.0);
cout << "Gaunt(1, 0, 1, 1, 0, 0) = ";
cout << GauntCoefficient(1, 0, 1, 1, 0, 0);
cout << endl;
cout << "Gaunt(1, 0, 1, 1, 0, -1) = ";
cout << GauntCoefficient(1, 0, 1, 1, 0, -1);
cout << endl;
real number = -1.0 / 2.0 / sqrtl(pi);
cout << "-1.0 / 2.0 / sqrt(pi) = ";
cout << number << endl;
return 0;
}
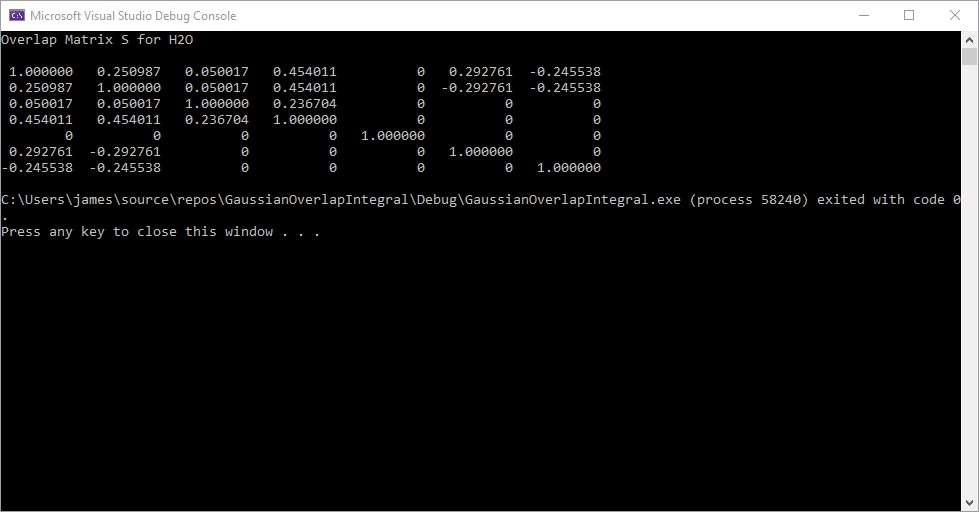
Blog Entry © Friday, November 1, 2024, by James Pate Williams, Jr. Calculation of the Overlap Matrix for the Water Molecule (H2O) Using a Contracted Set of Gaussian Orbitals
Reference: https://content.wolfram.com/sites/19/2012/02/Ho.pdf
I reproduced most of the computations in the MATHMATICA reference. The water molecule is a planar molecule that lies in the YZ-plane.