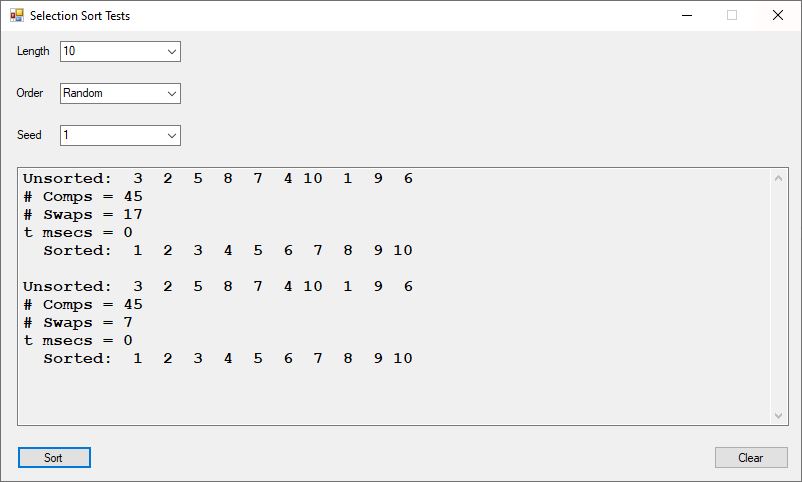
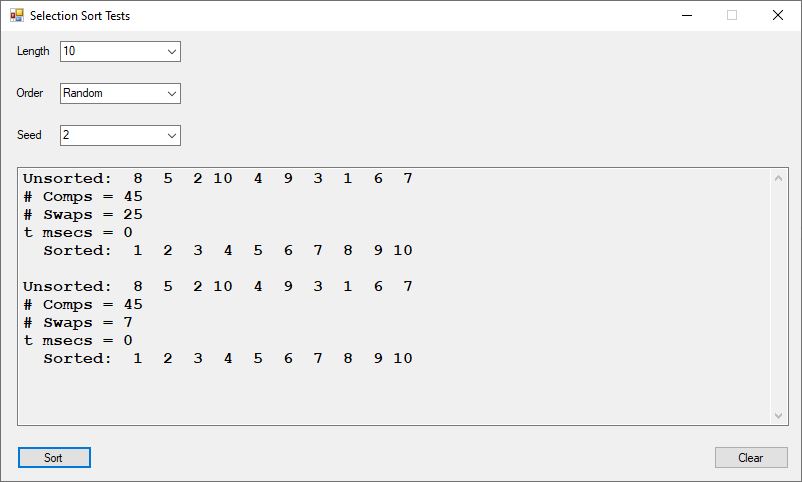
Sorting Algorithms – Page 2 – Numerical Explorations

Word to Word Game by James Pate Williams, Jr.

I implemented a computerized version of a game similar to the board game Boggle. Given a jumble of letters find as many words as possible. Suppose we have the jumbled letters “sldfie” then my C++ program outputs:

Now suppose the scrambled letters are “nifrsmo”:

The program uses permutations and power sets. All permutations of the set of three numbers 1, 2, and 3 are:

123 132 213 231 312 321

The total number of permutations of n objects is n! where n! = n * (n – 1) * … * 2 * 1. So we have 3! = 3 * 2 * 1 = 6 and 4! = 4 * 3 * 2 * 1 = 24.

A power set of three objects can generated by using the binary representation of all binary numbers 0 to 2 * 2 * 2 – 1 = 8 – 1 = 7.

0 = 000, 1 = 001, 2 = 010, 3 = 011, 4 = 100, 5 = 101, 6 = 110, and 7 = 111

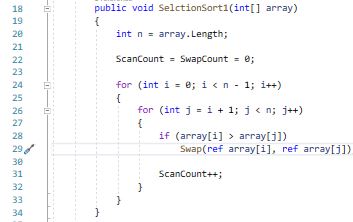
My main C++ function in the implementation is as follows:

vector<string> PowerSet(char cstr[], int len)
{
    vector<int> index;
    vector<string> match;

    for (long ps = 0; ps <= pow(2, len); ps++)
    {
        string str = ConvertBase2(cstr, ps, len);
        int psf = 1;

        for (int i = 2; i <= len; i++)
            psf *= i;

        for (int i = 0; i < psf; i++)
        {
            if (binary_search(dictWords.begin(), dictWords.end(), str))
            {
                if (!binary_search(match.begin(), match.end(), str))
                {
                    match.push_back(str);
                    sort(match.begin(), match.end());
                }
            }

            next_permutation(str.begin(), str.end());
        }
    }

    return match;
}

More Tests of two Selection Sort Implementations

In our last blog we introduced two algorithms for implementing the selection sort which differed by the number of swap operations involved. The two required the same number of comparisons n * (n – 1) / 2 = 45 for n = 10, where n is the length of the array to be sorted and different number of swaps. We notice about a two-fold speed up in sorting using the minimal number of swaps version. Also make sure the number of swaps is implemented by a 64-bit integer since 100,000 * 99,999 = 9,999,899,999 which overflows a 32-bit integer. I learned about overflow while trying to sort large arrays of integers.

Who Knew? Better Code for Selection Sort

I have been using inferior code for the Selection Sort since 1979. Last night I found the more efficient pseudo code:

Data Structure and Algorithms Selection Sort – Tutorialspoint

Here is my old code for the Selection Sort in C#:

And my new code from the more efficient pseudo code found online:

Both implementations require n * (n – 1) / 2 comparisons which for an array of length 15 is 15 * 14 /2 = 15 * 7 = 105. The second implementation requires typically fewer calls to the swap function.

Selection Sort Test 15-Element Random Array

Selection Sort Test 15-Element Reverse Ordered Array

Selection Sort Test 15-Element Sorted Array

The first number after the unsorted array is the number of comparisons which is always 105 in our 15-element test cases. The second number is the tally of the swap function calls.

Singleton’s Sorting Algorithm 1979 and 2018 by James Pate Williams, Jr., BS, BS, MSwE, PhD

I first implemented Singleton’s sorting algorithm in the Summer of 1979. The programming language was Data General’s version of Dayton BASIC (Beginner’s All-purpose Symbolic Instruction Code). This variant of BASIC was interpretive like C#, Java, and Pascal. Below is my BASIC version and run-times for double precision numbers in an inverted sequence.

Summer of 1979 BASIC Singleton’s Sorting Algorithm

Zoom forward to my current computer and C# programming language in 2018.

C# Singleton’s Sorting Algorithm 2008 – 2018 Random Lists of Double Precision Numbers

Two of My Many Sorting Algorithms Implementations by James Pate Williams, Jr. BA, BS, MSwE, PhD

A recurring theme in my life has been to implement and re-implement the sorting algorithms found in Harold Lorin’s treatise Sorting and Sort Systems and Thomas H. Corman et al.’s Algorithms. I purchased a copy of Lorin’s book in the summer of 1979 and Corman’s textbook in 1999 or 2000. This has been good exercise in translating from one computer language to a later and greater newer computer language. I began in BASIC and FORTRAN IV and transitioned to C, C++, C#, Common LISP, Java, Modula-2, Pascal, and Scheme in alphabetic not chronological order. In this blog we cover two C# applications, one from October 26, 2010, named Sorting Comparisons and the other from January 17, 2015, with the moniker Sorting.

In the Sorting Comparisons application, we compare the sorting algorithms: Heap Sort, Quick Sort, and Singleton’s Sort. The first two algorithms are from the Algorithms tome and Singleton’s Sort is from Lorin’s treatment. These are some of the fastest general purpose sorting algorithms available in my particular arsenal.

Sorting Comparisons Test All 16 Sorting Comparisons Time All 1000