Category: Uncategorized

Numerical Two-Dimensional Quadrature (Integration) by James Pate Williams, Jr.

Back in 2022 I performed some numerical experiments using the two-dimensional quadrature methods: Simpson’s Rule and Monte Carlo. I implemented both sequential and multitasking techniques. The integration algorithms were applied to electron-electron repulsion integrals and a two-dimensional exponential function. The two-dimensional exponential function has an exact value of pi divided by 4. The multitasking speed-up is about two-fold in the Simpson’s Rule case and almost three-fold in the Monte Carlo case.

Scale Model Construction Suggestions by James Pate Williams, Jr.

  1. After opening the box and making sure all pieces are on their numbered tree (sprue), read and study all the instructions.
  2. I like to paint the pieces while the part is on its tree.
  3. Make notes by grouping the pieces by color.
  4. I like to use acrylic paints nowadays (way back when I used enamel and enamel aerosol spray cans). Acrylic paint is easy to clean up and cures (completely dries) faster than enamel paint.
  5. Do subassemblies according to the instructions. Sometimes it is good to look ahead and make sure the assembly is facile.
  6. Do not wait until the model is finished to apply decals.
  7. Not everyone will have the artistic talent  to create a museum worthy model. Be satisfied with your current modeling ability. Happy scale modeling!

I took up plastic scale modeling again in about 2017 at the age of around 64. Here is a list of my models and some notes about their construction. All of my relatively modern models are by Revell:

  1. USS Arizona – To accurately build the hull tape off the armor belt and apply black paint. This model was painted with Testors enamel paint.
  2. USAAF B-17G Flying Fortress heavy bomber 1:48 scale. Use rubber bands and clothes pins to make sure the fuselage halves seal nicely.
  3. USN or USMC Vought F4U Corsair 1:48 scale. Be careful with the undercarriage. The landing gear is especially tricky to get correct.
  4. USAF Fairchild Republic A-10 Thunderbolt II “Warthog” 1:48 scale. I have not applied the plethora of decals. Please counterweights in the nose so the tricycle landing gear is accurate.
  5. McDonnell Douglas USMC or USN F/A-18 Hornet. Tricky landing gear assembly.
  6. Kriegsmarine Bismarck 1:350 scale. Many very small parts.
  7. Lockheed SR-71 Blackbird 1:48 scale. Lots of rather small decals. You can build different “Articles” (CIA lingo for the A-12 Archangel [Oxcart, Cygnus] and SR-71). The red no step decals are especially tricky to apply. Uses a lot of black paint.
  8. Apollo 11 Saturn V with the command module and lunar excursion module (LEM) 1:144 scale. Comes with three to scale engineers.
  9. USAAF Northup P-61 Black Widow 1:48 scale. The model comes in black plastic, so I did not paint the exterior. The radar in the nose is hard to get correctly seated.
  10. North American B-25J Mitchell medium bomber 1:48 scale. I am still working on this model.

If you have plenty of cash and patience, you can use spray paint. I prefer the somewhat inexpensive brush painting.

Battle of Thermopylae by James Pate Williams, Jr.

Battle of Thermopylae – World History Encyclopedia

“The Greek forces included 300 Spartans and their helots with 2,120 Arcadians, 1,000 Lokrians, 1,000 Phokians, 700 Thespians, 400 Corinthians, 400 Thebans, 200 men from Phleious, and 80 Mycenaeans.” The Persians led by Xerxes I were myriad.

There have been at least two large scale motion pictures made about the battle namely “The 300 Spartans (1962)” and the “300 (2006)”. I have seen both movies, but I prefer the 1962 version due to attempted adherence to Herodotus’ version of the history. The ending of the 1962 movie has a small remaining contingent of Spartans led by King Leonidas I dropping their shields in a mass suicide by a barrage of Persian arrows (“the sky was black with arrows”). “Oh stranger, tell the Spartans that we lie here obedient to their word.” The mantra of the Spartans was to come home to Sparta carrying their shields or to come home being carried dead on their shields. The 300 Spartans – Wikipedia

Latest Revell Model Build by James Pate Williams, Jr.

A few days ago, I finished my Revell 1:144 scale Apollo 11 and Saturn V plastic model. The kit had 82 parts and I used every one of the pieces. I deviated from the original paint scheme since the original black and white pattern is too reminiscent of Wehner von Braun’s World War II terror weapon, the V-2 also known as Retaliation Weapon 2. The V-2 was the first liquid propelled ballistic missile. It used ethanol as the fuel and liquid oxygen as the oxidizing agent.

https://en.wikipedia.org/wiki/V-2_rocket

The Saturn V used high-grade kerosene as the propellant and liquid oxygen as the oxidizing chemical.

https://en.wikipedia.org/wiki/Apollo_11

Here are some temporary photographs of my build.

https://share.icloud.com/photos/004LghGpS0wlijbfyqJv4GY6Q

Education

LaGrange College (1971 – 1972, 1976 – 79, BA Chemistry, GPA 3.08)

LaGrange College (1990 – 1994, BS Computer Science, GPA 4.00)

Georgia Institute of Technology (1980 – 1983, No Degree, GPA 2.79)

Auburn University (1998 – 2000, Master of Software Engineering, GPA 3.880)

Auburn University (2000 – 2005, Doctor of Philosophy, Computer Science, GPA 3.871)

New Knight’s Tour Application by James Pate Williams, Jr.

I created a new Win32 desktop C/C++ application to solve the Knight’s Tour. The app is limited to a six-by-six chessboard with any desired starting column and row. The user can choose between two algorithms to solve an instance of the problem, namely chronological backtracking and Warnsdorff method. A complete circuit or tour is found by both algorithms in between 30 and 40 seconds for backtracking and 2 to 3 seconds for the Warnsdorff method. The starting row is 3 and starting column 4 for to find a cyclic solution.

n-Body Solar System Software by James Pate Williams, Jr.

I have solved two planetary models of our solar system. The first was by approximating the Taylor series expansion for a n-body gravitational system. The approximate equations are given below:

n-body-problemDownload

The second computation used a fifth order Runge-Kutta method to solve the system of 3n second order non-linear ordinary differential equations. See the code below:

using System;
using System.Collections.Generic;
using System.ComponentModel;

namespace nBodyProblem
{
    public struct Vector3
    {
        public double x, y, z;
    }

    class nBodyTaylorSeries
    {
        private double G = 6.67384e-11;    // gravitational constant
        private int n;                     // number of masses
        private List<double> Mass;         // masses
        private List<Vector3> X0;          // initial positions
        private List<Vector3> V0;          // initial velocities

        public nBodyTaylorSeries(
            int n,
            List<double> Mass,
            List<Vector3> X0,
            List<Vector3> V0)
        {
            this.n = n;
            this.Mass = Mass;
            this.X0 = X0;
            this.V0 = V0;
        }

        private double Distance(Vector3 u, Vector3 v)
        {
            // Euclidean distance
            double uvxs = Math.Pow(u.x - v.x, 2);
            double uvys = Math.Pow(u.y - v.y, 2);
            double uvzs = Math.Pow(u.z - v.z, 2);

            return Math.Sqrt(uvxs + uvys + uvzs);
        }

        private Vector3 D2(
            int i,
            List<Vector3> X)
        {
            // second derivative at t0

            double sumX = 0, sumY = 0, sumZ = 0;
            Vector3 d2 = new Vector3();

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 3);
                    double m = Mass[k];

                    sumX += m * (X[k].x - X[i].x) / d;
                    sumY += m * (X[k].y - X[i].y) / d;
                    sumZ += m * (X[k].z - X[i].z) / d;
                }
            }

            d2.x = G * sumX;
            d2.y = G * sumY;
            d2.z = G * sumZ;
            return d2;
        }

        private Vector3 D3(
            int i,
            List<Vector3> X,
            List<Vector3> V)
        {
            // third derivative at t0

            double sumX1 = 0, sumY1 = 0, sumZ1 = 0;
            double sumX2 = 0, sumY2 = 0, sumZ2 = 0;
            Vector3 d3 = new Vector3();

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 3);
                    double m = Mass[k];

                    sumX1 += m * (V[k].x - V[i].x) / d;
                    sumY1 += m * (V[k].y - V[i].y) / d;
                    sumZ1 += m * (V[k].z - V[i].z) / d;
                }
            }

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 5);
                    double m = Mass[k];

                    sumX2 += m * (X[k].x - X[i].x) * (V[k].x - V[i].x) / d;
                    sumY2 += m * (X[k].y - X[i].y) * (V[k].y - V[i].y) / d;
                    sumZ2 += m * (X[k].z - X[i].z) * (V[k].z - V[i].z) / d;
                }
            }

            d3.x = G * (sumX1 - 1.5 * sumX2);
            d3.y = G * (sumY1 - 1.5 * sumY2);
            d3.z = G * (sumZ1 - 1.5 * sumZ2);
            return d3;
        }

        private Vector3 D4(
            int i,
            List<Vector3> X,
            List<Vector3> V,
            List<Vector3> A)
        {
            // fourth derivative at t0

            double sumX1 = 0, sumY1 = 0, sumZ1 = 0;
            double sumX2 = 0, sumY2 = 0, sumZ2 = 0;
            double sumX3 = 0, sumY3 = 0, sumZ3 = 0;
            double sumX4 = 0, sumY4 = 0, sumZ4 = 0;
            Vector3 d4 = new Vector3();

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 3);
                    double m = Mass[k];

                    sumX1 += m * (A[k].x - A[i].x) / d;
                    sumY1 += m * (A[k].y - A[i].y) / d;
                    sumZ1 += m * (A[k].z - A[i].z) / d;
                }
            }

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 5);
                    double m = Mass[k];

                    sumX2 += m * (X[k].x - X[i].x) * (A[k].x - A[i].x) / d;
                    sumY2 += m * (X[k].y - X[i].y) * (A[k].y - A[i].y) / d;
                    sumZ2 += m * (X[k].z - X[i].z) * (A[k].z - A[i].z) / d;
                }
            }

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 5);
                    double m = Mass[k];

                    sumX3 += m * Math.Pow(V[k].x - V[i].x, 2) / d;
                    sumY3 += m * Math.Pow(V[k].y - V[i].y, 2) / d;
                    sumZ3 += m * Math.Pow(V[k].z - V[i].z, 2) / d;
                }
            }

            for (int k = 0; k < n; k++)
            {
                if (k != i)
                {
                    double d = Math.Pow(Distance(X[k], X[i]), 7);
                    double m = Mass[k];

                    sumX4 += m * (X[k].x - X[i].x) * Math.Pow(V[k].x - V[i].x, 2) / d;
                    sumY4 += m * (X[k].y - X[i].y) * Math.Pow(V[k].y - V[i].y, 2) / d;
                    sumZ4 += m * (X[k].z - X[i].z) * Math.Pow(V[k].z - V[i].z, 2) / d;
                }
            }

            d4.x = G * (sumX1 - 1.5 * sumX2 - 3 * sumX3 + 15 * sumX4 / 4);
            d4.y = G * (sumY1 - 1.5 * sumY2 - 3 * sumY3 + 15 * sumY4 / 4);
            d4.z = G * (sumZ1 - 1.5 * sumZ2 - 3 * sumZ3 + 15 * sumZ4 / 4);
            return d4;
        }

        public Vector3 Position(
            int day0,
            int day1,
            int i,
            BackgroundWorker worker,
            DoWorkEventArgs e)
        {
            double t0 = day0 * 24 * 3600;
            double t1 = day1 * 24 * 3600;
            double delta = 60, t = t0;
            List<Vector3> Q0 = new List<Vector3>();
            List<Vector3> R0 = new List<Vector3>();

            for (int j = 0; j < n; j++)
            {
                Q0.Add(X0[j]);
                R0.Add(V0[j]);
            }

            while (t <= t1)
            {
                if (worker.CancellationPending)
                {
                    e.Cancel = true;
                    t = t1 + delta;
                }

                else
                {
                    List<Vector3> Q1 = new List<Vector3>();
                    List<Vector3> R1 = new List<Vector3>();
                    List<Vector3> d2 = new List<Vector3>();
                    List<Vector3> d3 = new List<Vector3>();
                    List<Vector3> d4 = new List<Vector3>();

                    for (int j = 0; j < n; j++)
                    {
                        // update derivatives
                        d2.Add(D2(j, Q0));
                        d3.Add(D3(j, Q0, R0));
                        Q1.Add(new Vector3());
                        R1.Add(new Vector3());
                    }

                    for (int j = 0; j < n; j++)
                        d4.Add(D4(i, Q0, R0, d2));

                    for (int j = 0; j < n; j++)
                    {
                        double m = Mass[j];
                        Vector3 Qj = new Vector3();
                        // update positions
                        Qj.x = Q0[j].x + delta * (R0[j].x + (delta * (d2[j].x / 2 + delta * (d3[j].x / 6 + delta * d4[j].x / 24)) / m));
                        Qj.y = Q0[j].y + delta * (R0[j].y + (delta * (d2[j].y / 2 + delta * (d3[j].y / 6 + delta * d4[j].y / 24)) / m));
                        Qj.z = Q0[j].z + delta * (R0[j].z + (delta * (d2[j].z / 2 + delta * (d3[j].z / 6 + delta * d4[j].z / 24)) / m));
                        Q1[j] = Qj;
                    }

                    for (int j = 0; j < n; j++)
                    {
                        double m = Mass[j];
                        Vector3 Rj = new Vector3();
                        // update velocities
                        Rj.x = R0[j].x + delta * (d2[j].x + delta * (d3[j].x / 2 + delta * d4[j].x / 6)) / m;
                        Rj.y = R0[j].y + delta * (d2[j].y + delta * (d3[j].y / 2 + delta * d4[j].y / 6)) / m;
                        Rj.z = R0[j].z + delta * (d2[j].z + delta * (d3[j].z / 2 + delta * d4[j].z / 6)) / m;
                        R1[j] = Rj;
                    }

                    for (int j = 0; j < n; j++)
                    {
                        Q0[j] = Q1[j];
                        R0[j] = R1[j];
                    }

                    t += delta;

                    int percentProgress = (int)(100 * t / t1);

                    worker.ReportProgress(percentProgress);
                }
            }

            // update positions and velocities
            X0 = new List<Vector3>();
            V0 = new List<Vector3>();

            for (int j = 0; j < n; j++)
            {
                X0.Add(Q0[j]);
                V0.Add(R0[j]);
            }

            return Q0[i];
        }
    }
}


using System;
using System.Collections.Generic;

namespace nBodyProblem
{
    public struct Vector3
    {
        public double x, y, z;
    }

    class RK3N
    {
        // function rk3n from "A Numerical Library in C for
        // Scientists and Engineers" by J.T. Lau PhD p. 465
        private void rk3n(ref double x, double a, double b,
            double[] y, double[] ya, double[] z, double[] za,
            Func<int, int, double, double[], double> fxyj,
            double[] e, double[] d, bool fi, int n)
        {
            bool first, last=false, reject, test, ta, tb;
            int j, jj;
            double xl, h, hmin, ind, hl=0, absh, fhm, discry, discrz, toly, tolz, mu, mu1=0, fhy, fhz;

            double[] yl = new double[n + 1];
            double[] zl = new double[n + 1];
            double[] k0 = new double[n + 1];
            double[] k1 = new double[n + 1];
            double[] k2 = new double[n + 1];
            double[] k3 = new double[n + 1];
            double[] k4 = new double[n + 1];
            double[] k5 = new double[n + 1];
            double[] ee = new double[4 * n + 1];

            if (fi)
            {
                d[3] = a;
                for (jj = 1; jj <= n; jj++)
                {
                    d[jj + 3] = ya[jj];
                    d[n + jj + 3] = za[jj];
                }
            }
            d[1] = 0.0;
            xl = d[3];
            for (jj = 1; jj <= n; jj++)
            {
                yl[jj] = d[jj + 3];
                zl[jj] = d[n + jj + 3];
            }
            if (fi) d[2] = b - d[3];
            absh = h = Math.Abs(d[2]);
            if (b - xl < 0.0) h = -h;
            ind = Math.Abs(b - xl);
            hmin = ind * e[1] + e[2];
            for (jj = 2; jj <= 2 * n; jj++)
            {
                hl = ind * e[2 * jj - 1] + e[2 * jj];
                if (hl < hmin) hmin = hl;
            }
            for (jj = 1; jj <= 4 * n; jj++) ee[jj] = e[jj] / ind;
            first = reject = true;
            test = true;
            if (fi)
            {
                last = true;
                test = false;
            }
            while (true)
            {
                if (test)
                {
                    absh = Math.Abs(h);
                    if (absh < hmin)
                    {
                        h = (h > 0.0) ? hmin : -hmin;
                        absh = hmin;
                    }
                    ta = (h >= b - xl);
                    tb = (h >= 0.0);
                    if ((ta && tb) || (!(ta || tb)))
                    {
                        d[2] = h;
                        last = true;
                        h = b - xl;
                        absh = Math.Abs(h);
                    }
                    else
                        last = false;
                }
                test = true;
                if (reject)
                {
                    x = xl;
                    for (jj = 1; jj <= n; jj++) y[jj] = yl[jj];
                    for (j = 1; j <= n; j++) k0[j] = fxyj(n, j, x, y) * h;
                }
                else
                {
                    fhy = h / hl;
                    for (jj = 1; jj <= n; jj++) k0[jj] = k5[jj] * fhy;
                }
                x = xl + 0.276393202250021 * h;
                for (jj = 1; jj <= n; jj++)
                    y[jj] = yl[jj] + (zl[jj] * 0.276393202250021 +
                                    k0[jj] * 0.038196601125011) * h;
                for (j = 1; j <= n; j++) k1[j] = fxyj(n, j, x, y) * h;
                x = xl + 0.723606797749979 * h;
                for (jj = 1; jj <= n; jj++)
                    y[jj] = yl[jj] + (zl[jj] * 0.723606797749979 +
                                    k1[jj] * 0.261803398874989) * h;
                for (j = 1; j <= n; j++) k2[j] = fxyj(n, j, x, y) * h;
                x = xl + h * 0.5;
                for (jj = 1; jj <= n; jj++)
                    y[jj] = yl[jj] + (zl[jj] * 0.5 + k0[jj] * 0.046875 + k1[jj] *
                            0.079824155839840 - k2[jj] * 0.001699155839840) * h;
                for (j = 1; j <= n; j++) k4[j] = fxyj(n, j, x, y) * h;
                x = (last ? b : xl + h);
                for (jj = 1; jj <= n; jj++)
                    y[jj] = yl[jj] + (zl[jj] + k0[jj] * 0.309016994374947 +
                                    k2[jj] * 0.190983005625053) * h;
                for (j = 1; j <= n; j++) k3[j] = fxyj(n, j, x, y) * h;
                for (jj = 1; jj <= n; jj++)
                    y[jj] = yl[jj] + (zl[jj] + k0[jj] * 0.083333333333333 + k1[jj] *
                            0.301502832395825 + k2[jj] * 0.115163834270842) * h;
                for (j = 1; j <= n; j++) k5[j] = fxyj(n, j, x, y) * h;
                reject =false;
                fhm = 0.0;
                for (jj = 1; jj <= n; jj++)
                {
                    discry = Math.Abs((-k0[jj] * 0.5 + k1[jj] * 1.809016994374947 +
                                k2[jj] * 0.690983005625053 - k4[jj] * 2.0) * h);
                    discrz = Math.Abs((k0[jj] - k3[jj]) * 2.0 - (k1[jj] + k2[jj]) * 10.0 +
                                k4[jj] * 16.0 + k5[jj] * 4.0);
                    toly = absh * (Math.Abs(zl[jj]) * ee[2 * jj - 1] + ee[2 * jj]);
                    tolz = Math.Abs(k0[jj]) * ee[2 * (jj + n) - 1] + absh * ee[2 * (jj + n)];
                    reject = ((discry > toly) || (discrz > tolz) || reject);
                    fhy = discry / toly;
                    fhz = discrz / tolz;
                    if (fhz > fhy) fhy = fhz;
                    if (fhy > fhm) fhm = fhy;
                }
                mu = 1.0 / (1.0 + fhm) + 0.45;
                if (reject)
                {
                    if (absh <= hmin)
                    {
                        d[1] += 1.0;
                        for (jj = 1; jj <= n; jj++)
                        {
                            y[jj] = yl[jj];
                            z[jj] = zl[jj];
                        }
                        first = true;
                        if (b == x) break;
                        xl = x;
                        for (jj = 1; jj <= n; jj++)
                        {
                            yl[jj] = y[jj];
                            zl[jj] = z[jj];
                        }
                    }
                    else
                        h *= mu;
                }
                else
                {
                    if (first)
                    {
                        first = false;
                        hl = h;
                        h *= mu;
                    }
                    else
                    {
                        fhy = mu * h / hl + mu - mu1;
                        hl = h;
                        h *= fhy;
                    }
                    mu1 = mu;
                    for (jj = 1; jj <= n; jj++)
                        z[jj] = zl[jj] + (k0[jj] + k3[jj]) * 0.083333333333333 +
                            (k1[jj] + k2[jj]) * 0.416666666666667;
                    if (b == x) break;
                    xl = x;
                    for (jj = 1; jj <= n; jj++)
                    {
                        yl[jj] = y[jj];
                        zl[jj] = z[jj];
                    }
                }
            }
            if (!last) d[2] = h;
            d[3] = x;
            for (jj = 1; jj <= n; jj++)
            {
                d[jj + 3] = y[jj];
                d[n + jj + 3] = z[jj];
            }
        }

        // Euclidean distance
        private double distance(
            double x1,
            double y1,
            double z1,
            double x2,
            double y2,
            double z2)
        {
            double xs = Math.Pow(x1 - x2, 2);
            double ys = Math.Pow(y1 - y2, 2);
            double zs = Math.Pow(z1 - z2, 2);

            return Math.Sqrt(xs + ys + zs);
        }

        // n-body gravitational force
        private double ftxj(int n, int j, double t, double[] x)
        {
            double G = 6.67384e-11; // gravitational constant
            double sum = 0;
            int j3 = j / 3 + 1;
            int m3 = j % 3;

            // remember we are now working with 3n equations
            for (int k = 1; k <= n / 3; k++)
            {
                int k3 = 3 * (k - 1) + 1;

                double d = distance(
                    x[k3],
                    x[k3 + 1],
                    x[k3 + 2],
                    x[j3],
                    x[j3 + 1],
                    x[j3 + 2]);
                double denom = d * d * d;

                if (denom != 0)
                    sum += (x[k3 + m3] - x[j3 + m3]) / denom;
            }

            return G * sum;
        }

        public Vector3 nBody(
            int day0,
            int day1,
            int i,
            int n,
            List<double> Mass,
            ref List<Vector3> X0,
            ref List<Vector3> V0)
        {
            int n3 = 3 * n;                 // 3n equations n (x, y, z)
            double a = day0 * 24 * 3600;    // convert to seconds
            double b = day1 * 24 * 3600;    // convert to seconds
            double x = a;
            double[] y = new double[n3 + 1];
            double[] ya = new double[n3 + 1];
            double[] z = new double[n3 + 1];
            double[] za = new double[n3 + 1];
            double[] e = new double[4 * n3 + 1];
            double[] d = new double[2 * n3 + 4];

            // initialize error constraints
            for (int j = 0; j <= 4 * n3; j++)
                e[j] = 1.0e-12;

            // create a system of 3n equations
            for (int j = 0; j < n; j++)
            {
                int j3 = 3 * j;

                ya[j3 + 1] = X0[j].x;
                ya[j3 + 2] = X0[j].y;
                ya[j3 + 3] = X0[j].z;
                za[j3 + 1] = V0[j].x;
                za[j3 + 2] = V0[j].y;
                za[j3 + 3] = V0[j].z;
            }

            // solve the system of 3n ordinary differential equations
            rk3n(ref x, a, b, y, ya, z, za, ftxj, e, d, true, n3);
            // we return the position of the desired ith body
            Vector3 result = new Vector3();

            int i3 = 3 * i;

            result.x = y[i3 + 1];
            result.y = y[i3 + 2];
            result.z = y[i3 + 3];

            // update the positions and velocities
            // wipe the slates clean
            X0 = new List<Vector3>();
            V0 = new List<Vector3>();

            for (int j = 0; j < n; j++)
            {
                int j3 = 3 * j;
                Vector3 X = new Vector3();  // new position
                Vector3 V = new Vector3();  // new velocity

                X.x = y[j3 + 1];    // 3n position components
                X.y = y[j3 + 2];
                X.z = y[j3 + 3];
                V.x = z[j3 + 1];    // 3n velocity components
                V.y = z[j3 + 2];
                V.z = z[j3 + 3];
                // update vectors
                X0.Add(X);
                V0.Add(V);
            }

            return result;
        }
    }
}

Results will be added at a later date.

Six Large Integer Factoring Methods Using Arjen K. Lenstra’s Free Large Integer Package (Free LIP) by James Pate Wiliams, Jr.

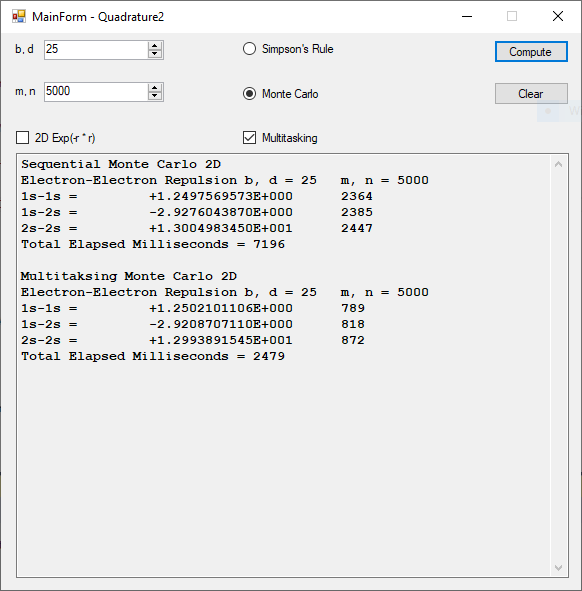
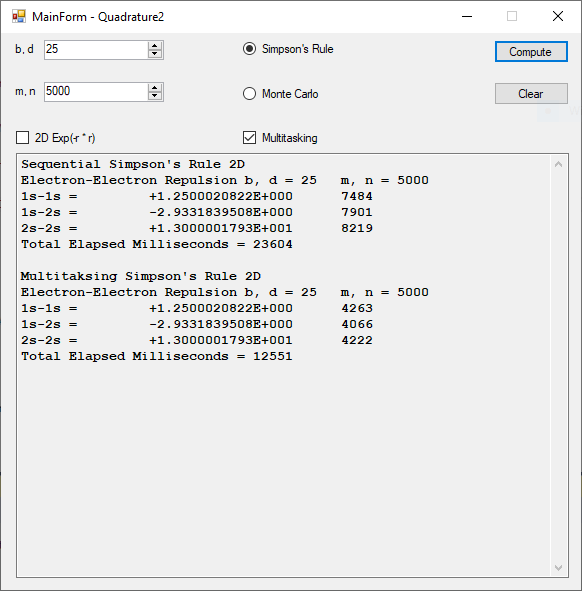
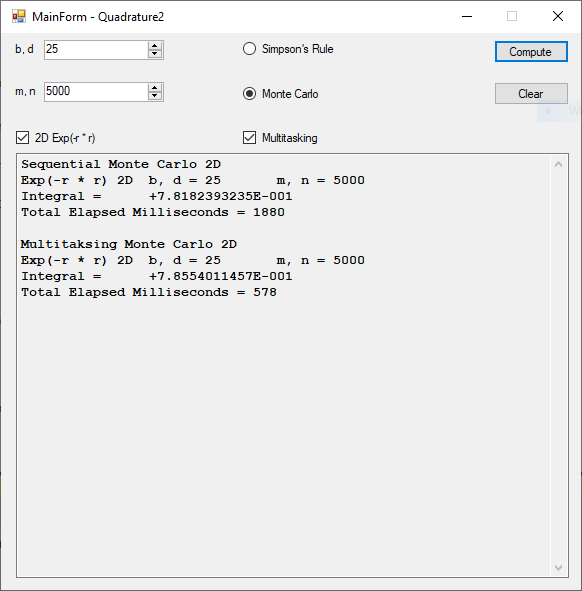
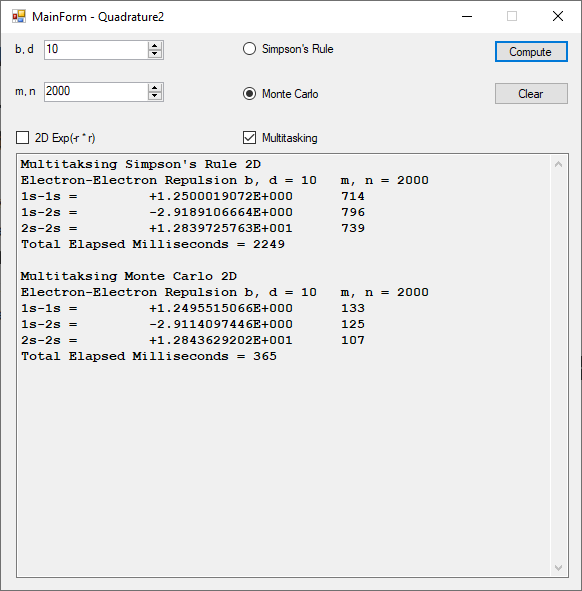
This C code uses singly linked lists as the key data structure. The factoring methods are trial division, Brent’s modification of the well-known Pollard rho method, Cohen-Pollard p – 1 algorithm first stage, Lehman’s method, Cohen’s algorithm for the Lenstra’s elliptic curve method, and the Free LIP elliptic curve method. I include a couple of sample factorizations by the Free LIP built-in Lenstra elliptic curve method. These include the seventh Fermat number 2^128+1 and the eighth Fermat number 2^256+1.

/*
Author:  Pate Williams (c) 1997

Algorithm 8.4.1 (Lehman). See "A Course in
Computational Algebraic Number Theory" by
Henri Cohen page 425.

Author:  Pate Williams (c) 1997 - 2022

Algorithm 8.5.2 (Pollard rho). See "A Course in
Computational Algebraic Number Theory" by Henri
Cohen page 429.

Author:  Pate Williams (c) 1997 - 2022

Algorithm 8.8.2 (p - 1 First Stage). See "A Course
in Computational Algebraic Number Theory" by Henri
Cohen page 439.

Author:  Pate Williams (c) 1997 - 2022

Algorithm 10.3.3 (Lenstra's ECM). See "A Course
in Computational Algebraic Number Theory" by
Henri Cohen page 488.
*/

#include "LIP_data_structures.h"
#include <crtdbg.h>

#ifndef CLK_TCK
#define CLK_TCK CLOCKS_PER_SEC
#endif

typedef struct myThreadData
{
	int zacount;
	verylong zn;
	PFACTORNODE current;
	PFACTORNODE first;
	PFACTORNODE(*tdFunction)(
		verylong*,
		PFACTORNODE,
		int*);
} THREADDATA, *PTHREADDATA;

DWORD WINAPI TdThread(LPVOID lpParam)
{
	clock_t time0 = clock();
	PTHREADDATA td = (PTHREADDATA)lpParam;
	PFACTORNODE head = td->first;
	td->current = td->tdFunction(
		&td->zn, td->first, &td->zacount);
	td->first = td->current;
	PFACTORNODE last = find_last(td->first);
	quick_sort(td->first, last);

	if (td->first != NULL)
	{
		while (td->first != NULL)
		{
			if (zprobprime(td->first->factor.zfactor, 20))
			{
				zwrite(td->first->factor.zfactor);

				if (td->first->factor.exponent > 1)
					printf(" ^ %d ", td->first->factor.exponent);

				printf("\n");
			}
			
			td->first = td->first->next;
		}
	}

	PFACTORNODE ptr = head;

	while (ptr != NULL)
	{
		ptr = delete_factor_node(head);
		head = ptr;
	}

	double time = (clock() - time0) / (double)CLK_TCK;
	printf("total time required: %f seconds\n", time);
	return TRUE;
}

int main()
{
	int i = 0, zacount = 0;
	verylong zN = 0, zf = 0, zn = 0, zo = 0;
	verylong zaddend = 0, zbase = 0, ztemp = 0;
	verylong zq = 0, zr = 0, zs = 0;
	PFACTORNODE current = NULL, first = NULL;

	while (1)
	{
		char optionStr[256], numStr[256] = { 0 }, option, *bPtr, *ePtr;
		int base, expon, addend, iExpon = 0, positive;

		printf("Menu\n");
		printf("1 Trial Division\n");
		printf("2 Brent-Pollard rho Method\n");
		printf("3 Cohen-Pollard p - 1 Method\n");
		printf("4 Lehman's Method\n");
		printf("5 Cohen Lenstra's Elliptic Curve Method\n");
		printf("6 FreeLIP Lenstra's Elliptic Curve Method\n");
		printf("7 Exit\n");
		printf("Enter choice (1 - 7): ");
		scanf_s("%s", optionStr, 256);
		option = optionStr[0];

		zone(&zo);

		if (option == '7')
			break;

		if (option < '1' || option > '6')
		{
			printf("Unknown choice, please reenter choice\n");
			continue;
		}

		printf("enter the number below (0 to quit):\n");
		scanf_s("%s", numStr, 256);

		bPtr = strchr(numStr, '^');

		if (bPtr != NULL)
		{
			*bPtr = '\0';
			base = atoi(numStr);
			ePtr = strchr(bPtr + 1, '+');

			if (ePtr != NULL)
				positive = 1;

			else {
				ePtr = strchr(bPtr + 1, '-');

				if (ePtr != NULL)
					positive = 0;
			}

			if (ePtr != NULL)
				*ePtr = '\0';

			expon = atoi(bPtr + 1);

			if (ePtr != NULL) {
				addend = atoi(ePtr + 1);

				if (positive == 0)
					addend = -addend;
			}

			else
				addend = 0;

			zintoz(base, &zbase);
			zintoz(addend, &zaddend);
			zsexp(zbase, expon, &ztemp);
			zadd(ztemp, zaddend, &zN);

			numStr[0] = '\0';
		}

		else
			zstrtoz(numStr, &zN);

		zcopy(zN, &zn);

		if (zmcomposite(zn, 20) == 0)
		{
			printf("Number is prime\n");
			continue;
		}

		first = insert_first_factor_node(zo, 0);
		zacount = 1;

		DWORD dwMilliseconds;
		PTHREADDATA pThreadData = (PTHREADDATA)
			malloc(sizeof(THREADDATA));

		if (pThreadData == NULL)
			exit(0);

		memset(pThreadData, 0, sizeof(THREADDATA));

		pThreadData->current = NULL;
		pThreadData->first = first;
		pThreadData->zacount = 1;
		zcopy(zn, &pThreadData->zn);

		printf("Wait milliseconds = ");
		scanf_s("%ld", &dwMilliseconds);

		if (option == '1')
		{
			pThreadData->tdFunction = trial_division;

			DWORD threadId;
			HANDLE hMutex = CreateMutex(
				NULL, FALSE, NULL);

			if (hMutex == NULL)
				exit(0);

			HANDLE thread = CreateThread(
				NULL,
				0,
				(LPTHREAD_START_ROUTINE)TdThread,
				pThreadData,
				0,
				&threadId);

			WaitForSingleObject(thread, dwMilliseconds);
			CloseHandle(thread);
			CloseHandle(hMutex);
		}

		else if (option == '2')
		{
			pThreadData->tdFunction = Brent_Pollard_Method;

			DWORD threadId;
			HANDLE hMutex = CreateMutex(
				NULL, FALSE, NULL);

			if (hMutex == NULL)
				exit(0);

			HANDLE thread = CreateThread(
				NULL,
				0,
				(LPTHREAD_START_ROUTINE)TdThread,
				pThreadData,
				0,
				&threadId);

			if (thread == NULL)
				exit(0);

			WaitForSingleObject(thread, dwMilliseconds);
			CloseHandle(thread);
			CloseHandle(hMutex);
		}

		else if (option == '3')
		{
			pThreadData->tdFunction = Cohen_Pollard_Method;

			DWORD threadId;
			HANDLE hMutex = CreateMutex(
				NULL, FALSE, NULL);

			if (hMutex == NULL)
				exit(0);

			HANDLE thread = CreateThread(
				NULL,
				0,
				(LPTHREAD_START_ROUTINE)TdThread,
				pThreadData,
				0,
				&threadId);

			WaitForSingleObject(thread, dwMilliseconds);
			CloseHandle(thread);
			CloseHandle(hMutex);
		}

		else if (option == '4')
		{
			pThreadData->tdFunction = Lehman;

			DWORD threadId;
			HANDLE hMutex = CreateMutex(
				NULL, FALSE, NULL);

			if (hMutex == NULL)
				exit(0);

			HANDLE thread = CreateThread(
				NULL,
				0,
				(LPTHREAD_START_ROUTINE)TdThread,
				pThreadData,
				0,
				&threadId);

			WaitForSingleObject(thread, dwMilliseconds);
			CloseHandle(thread);
			CloseHandle(hMutex);
		}

		else if (option == '5')
		{
			first = CohenEllipticCurveMethod(
				numStr, base, expon, addend);
		}

		else if (option == '6')
		{
			pThreadData->tdFunction = LenstraEllipticCurveMethod;

			DWORD threadId;
			HANDLE hMutex = CreateMutex(
				NULL, FALSE, NULL);

			if (hMutex == NULL)
				exit(0);

			HANDLE thread = CreateThread(
				NULL,
				0,
				(LPTHREAD_START_ROUTINE)TdThread,
				pThreadData,
				0,
				&threadId);

			WaitForSingleObject(thread, dwMilliseconds);
			CloseHandle(thread);
			CloseHandle(hMutex);
		}

		zfree(&pThreadData->zn);
		free(pThreadData);
	}

	zfree(&zaddend);
	zfree(&zbase);
	zfree(&ztemp);
	zfree(&zN);
	zfree(&zf);
	zfree(&zn);
	zfree(&zo);
	zfree(&zq);
	zfree(&zr);
	zfree(&zs);
	return 1;
}

#pragma once
#include "..\LIPFactoring\lip.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

#define my_B 1000000l
#define my_NUMBER_PRIMES 78498l
#define my_BOUND 100000000l

/* https://www.tutorialspoint.com/data_structures_algorithms/linked_list_program_in_c.htm */
/* https://www.geeksforgeeks.org/quicksort-on-singly-linked-list */

typedef struct my_factor
{
	long exponent;		// secondary storage key
	verylong zfactor;	// primary storage key
} FACTOR, *PFACTOR;

typedef struct my_factor_node
{
	FACTOR factor;
	struct my_factor_node* next;
} FACTORNODE, *PFACTORNODE;

/* basic singly linked list functions
** the c means complete comparison including
** the exponents of the factor or factor_node
** s denotes a shallow comparison */
int factor_z_compare_c(FACTOR lt, FACTOR rt);
int factor_z_compare_s(FACTOR lt, FACTOR rt);
int factor_node_z_compare_c(FACTORNODE lt, FACTORNODE rt);
int factor_node_z_compare_s(FACTORNODE lt, FACTORNODE rt);
PFACTORNODE insert_first_factor_node(verylong zf, int exponent);
PFACTORNODE insert_factor_node(PFACTORNODE current, FACTOR factor);
PFACTORNODE delete_factor_node(PFACTORNODE first);
PFACTORNODE linear_search_factor_c(PFACTORNODE first, FACTOR factor);
PFACTORNODE linear_search_factor_s(PFACTORNODE first, FACTOR factor);
void reverse(PFACTORNODE* first_ref);
// old school factoring algorithms
PFACTORNODE trial_division(verylong *zN, PFACTORNODE fn, int *count);
int trial_division_1(long B, verylong *zN, verylong *zf);
PFACTORNODE Brent_Pollard_Method(verylong *zN, PFACTORNODE fn, int *count);
PFACTORNODE Cohen_Pollard_Method(verylong *zN, PFACTORNODE fn, int *count);
PFACTORNODE Lehman(verylong *zN, PFACTORNODE fn, int *count);
PFACTORNODE find_last(PFACTORNODE first);
void quick_sort(PFACTORNODE first, PFACTORNODE last);

/* Lenstra's Elliptic Curve Method define and point structure */

#define CURVES 1024l

typedef struct ec_point
{ 
	verylong zx, zy, zz;
} ECPOINT, *PECPOINT;

PFACTORNODE CohenEllipticCurveMethod(
	char *numStr, int base, int expon, int addend);

PFACTORNODE LenstraEllipticCurveMethod(
	verylong *zN, PFACTORNODE first, int *count);

#include "LIP_data_structures.h"

/* complete factor comparison */

int factor_z_compare_c(FACTOR lt, FACTOR rt)
{
	verylong zlt, zrt;
	
	zcopy(lt.zfactor, &zlt);
	zcopy(rt.zfactor, &zrt);
	int zc = zcompare(zlt, zrt);
	
	if (zc > 0)
		return +1;
	if (zc < 0)
		return -1;
	if (lt.exponent < rt.exponent)
		return -1;
	if (lt.exponent > rt.exponent)
		return -1;
	
	return 0;
}

/* shallow factor comparison */

int factor_z_compare_s(FACTOR lt, FACTOR rt)
{
	verylong zlt = 0, zrt = 0;

	zcopy(lt.zfactor, &zlt);
	zcopy(rt.zfactor, &zrt);
	int zc = zcompare(zlt, zrt);

	if (zc > 0)
		return +1;
	if (zc < 0)
		return -1;

	return 0;
}

/* complete factor_node comparison */

int factor_node_z_compare_c(FACTORNODE lt, FACTORNODE rt)
{
	verylong zlt, zrt;

	zcopy(lt.factor.zfactor, &zlt);
	zcopy(rt.factor.zfactor, &zrt);
	int zc = zcompare(zlt, zrt);

	if (zc > 0)
		return +1;
	if (zc < 0)
		return -1;
	if (lt.factor.exponent < rt.factor.exponent)
		return -1;
	if (lt.factor.exponent > rt.factor.exponent)
		return -1;

	return 0;
}

/* shallow factor node comparison */

int factor_node_z_compare_s(FACTORNODE lt, FACTORNODE rt)
{
	verylong zlt, zrt;

	zcopy(lt.factor.zfactor, &zlt);
	zcopy(rt.factor.zfactor, &zrt);
	int zc = zcompare(zlt, zrt);

	if (zc > 0)
		return +1;
	if (zc < 0)
		return -1;

	return 0;
}

/* returns the first factor node */

PFACTORNODE insert_first_factor_node(verylong zf, int exponent)
{
	PFACTORNODE first = (PFACTORNODE) malloc(sizeof(FACTORNODE));
	
	memset(first, 0, sizeof(FACTORNODE));
	zcopy(zf, &first->factor.zfactor);
	first->factor.exponent = exponent;
	first->next = NULL;
	return first;
}

/* insert a factor node in order */

PFACTORNODE insert_factor_node(PFACTORNODE first, FACTOR factor)
{
	if (first == NULL)
		return NULL;

	PFACTORNODE next = (PFACTORNODE)malloc(sizeof(FACTORNODE));

	memset(next, 0, sizeof(FACTORNODE));
	next->factor.exponent = factor.exponent;
	zcopy(factor.zfactor, &next->factor.zfactor);
	next->next = first;
	return next;
}

PFACTORNODE delete_factor_node(PFACTORNODE first)
{
	if (first == NULL)
		return NULL;

	PFACTORNODE toDelete = first;

	first = first->next;

	zfree(&toDelete->factor.zfactor);
	free(toDelete);
	return first;
}

PFACTORNODE linear_search_factor_c(PFACTORNODE first, FACTOR factor)
{
	int found = 0;
	PFACTORNODE ptr = first;

	if (ptr == NULL)
		return NULL;

	do
	{
		found = factor_z_compare_c(ptr->factor, factor);

		if (found == 0)
			return ptr;
		else
			ptr = ptr->next;

	} while (ptr != NULL);

	return NULL;
}

void reverse(PFACTORNODE* first_ref)
{
	PFACTORNODE prev = NULL;
	PFACTORNODE current = *first_ref;
	PFACTORNODE next;

	while (current != NULL) {
		next = current->next;
		current->next = prev;
		prev = current;
		current = next;
	}

	*first_ref = prev;
}


PFACTORNODE linear_search_factor_s(PFACTORNODE first, FACTOR factor)
{
	int found = 0;
	PFACTORNODE ptr = first;

	if (ptr == NULL)
		return NULL;

	do
	{
		found = factor_z_compare_s(ptr->factor, factor);

		if (found == 0)
			return ptr;
		else
			ptr = ptr->next;

	} while (ptr != NULL);

	return NULL;
}

PFACTORNODE partition(PFACTORNODE first, PFACTORNODE last)
{
	if (first == last || first == NULL || last == NULL)
		return first;

	PFACTORNODE pivot = first;
	PFACTORNODE front = first;
	FACTOR temp;

	while (front != NULL && front != last)
	{
		if (zcompare(
			front->factor.zfactor, last->factor.zfactor) < 0) {
			pivot = first;
			temp = first->factor;
			first->factor = front->factor;
			front->factor = temp;

			first = first->next;
		}

		front = front->next;
	}

	temp = first->factor;
	first->factor = last->factor;
	last->factor = temp;
	return pivot;
}

PFACTORNODE find_last(PFACTORNODE first)
{
	while (first->next != NULL)
	{
		first = first->next;
	}

	return first;
}

void quick_sort(PFACTORNODE first, PFACTORNODE last)
{
	if (first == last) {
		return;
	}

	PFACTORNODE pivot = partition(first, last);

	if (pivot != NULL && pivot->next != NULL) {
		quick_sort(pivot->next, last);
	}

	if (pivot != NULL && first != pivot) {
		quick_sort(first, pivot);
	}
}

PFACTORNODE do_Brent_Pollard(verylong *zN, PFACTORNODE first, int *count)
{
	int e, one, pr;
	long c, i, k, l;
	verylong zP = 0, za = 0, zb = 0, zg = 0, zn = 0;
	verylong zx = 0, zx1 = 0, zy = 0;
	FACTOR factor;
	PFACTORNODE current = NULL;

	zcopy(*zN, &zn);

	do {
		c = 0, k = l = 1;
		zone(&zP);
		zintoz(2l, &zy);
		zintoz(2l, &zx);
		zintoz(2l, &zx1);
	L2:
		zsq(zx, &za);
		zsadd(za, 1l, &zb);
		zmod(zb, zn, &zx);
		zsub(zx1, zx, &za);
		zmulmod(za, zP, zn, &zb);
		zcopy(zb, &zP);

		if (++c == 20) {
			zgcd(zP, zn, &zg);
			
			if (zscompare(zg, 1l) > 0)
				goto L4;
			
			zcopy(zx, &zy);
			c = 0;
		}

		if (--k != 0)
			goto L2;

		zgcd(zP, zn, &zg);

		if (zscompare(zg, 1l) > 0)
			goto L4;

		zcopy(zx, &zx1);
		k = l, l *= 2;

		for (i = 0; i < k; i++)
		{
			zsq(zx, &za);
			zsadd(za, 1l, &zb);
			zmod(zb, zn, &zx);
		}

		zcopy(zx, &zy);
		c = 0;

		goto L2;
	L4:
		do {
			zsq(zy, &za);
			zsadd(za, 1l, &zb);
			zmod(zb, zn, &zy);
			zsub(zx1, zy, &za);
			zgcd(za, zn, &zg);
		} while (zscompare(zg, 1l) == 0);

		if (zcompare(zg, zn) == 0)
		{
			fprintf(stderr, "fatal error\nBrent's method failed\n");
			exit(1);
		}

		if (!zprobprime(zg, 20l))
		{
			zcopy(zg, &za);

			if ((current = trial_division(&zg, first, count)) == NULL) {
				fprintf(stderr, "fatal error\ncould not trial divide\n");
				exit(1);
			}

			first = current;
			zcopy(za, &zg);
			zdiv(zn, zg, &za, &zb);
			zcopy(za, &zn);
		}

		else
		{
			e = 0;

			do {
				zdiv(zn, zg, &za, &zb);
				zcopy(za, &zn);
				zmod(zn, zg, &za);
				e++;
			} while (zscompare(za, 0l) == 0);

			if (first != NULL)
			{
				factor.exponent = e;
				factor.zfactor = 0;
				zcopy(zg, &factor.zfactor);
				current = insert_factor_node(first, factor);
				first = current;
				*count = *count + 1;
			}
		}
		
		one = zscompare(zn, 1l) == 0;

		if (!one)
		{
			pr = zprobprime(zn, 20l);

			if (pr)
			{
				factor.exponent = 1;
				factor.zfactor = 0;
				zcopy(zn, &factor.zfactor);
				current = insert_factor_node(first, factor);
				first = current;
				break;
			}
		}
	} while (!one);

	zfree(&zP);
	zfree(&za);
	zfree(&zb);
	zfree(&zg);
	zfree(&zn);
	zfree(&zx);
	zfree(&zx1);
	zfree(&zy);
	return first;
}

PFACTORNODE Brent_Pollard_Method(
	verylong *zN,
	PFACTORNODE first,
	int *count)
{
	verylong zq = 0, zr = 0;
	FACTOR factor;
	PFACTORNODE current = NULL, ptr;

	*count = 0;

	while (1)
	{
		current = do_Brent_Pollard(zN, first, count);
		first = current;
		ptr = first;

		while (ptr != NULL)
		{
			zdiv(*zN, ptr->factor.zfactor, &zq, &zr);

			while (zscompare(zr, 0l))
			{
				zdiv(zq, ptr->factor.zfactor, &zq, &zr);
			}

			if (zscompare(zq, 1l))
				goto out_loop;

			if (zprobprime(zq, 20l))
				goto out_loop;

			ptr = ptr->next;
		}

		if (zscompare(*zN, 1l) == 0)
			return first;

		if (zprobprime(*zN, 20l) > 0)
			break;
	}
out_loop:
	zfree(&zq);
	zfree(&zr);
	factor.exponent = 1;
	factor.zfactor = 0;
	zcopy(*zN, &factor.zfactor);
	current = insert_factor_node(first, factor);
	first = current;
	return first;
}

PFACTORNODE first_stage(long k, verylong *zN, long x0, long *p,
	verylong *zx, PFACTORNODE first, int *count)
{
	long c = 0, i = -1, j = i, l, q, q1;
	static verylong zg = 0, zq1 = 0, zt = 0, zx1 = 0, zy = 0;
	FACTOR factor;
	PFACTORNODE current = NULL;

	*count = 0;
	zzero(&zg);
	zsadd(zg, x0, zx);
	zcopy(*zx, &zy);
L2:
	i++;
	if (i > k) {
		zsadd(*zx, -1l, &zx1);
		zgcd(zx1, *zN, &zg);
		if (zscompare(zg, 1l) == 0) return NULL;
		else {
			i = j;
			zcopy(zy, zx);
			goto L5;
		}
	}
	else {
		q = p[i];
		q1 = q;
		l = my_B / q;
	}

	while (q1 <= l) q1 *= q;
	zzero(&zt);
	zsadd(zt, q1, &zq1);
	zcopy(*zx, &zt);
	zexpmod(zt, zq1, *zN, zx);
	if (++c < 20) goto L2;
	zsadd(*zx, -1l, &zx1);
	zgcd(zx1, *zN, &zg);
	if (zscompare(zg, 1l) == 0) {
		c = 0;
		j = i;
		zcopy(*zx, &zy);
		goto L2;
	}
	else {
		i = j;
		zcopy(zy, zx);
	}
L5:
	i++;
	q = p[i];
	q1 = q;
L6:
	zzero(&zt);
	zsadd(zt, q, &zq1);
	zcopy(*zx, &zt);
	zexpmod(zt, zq1, *zN, zx);
	zsadd(*zx, -1l, &zx1);
	zgcd(zx1, *zN, &zg);
	if (zscompare(zg, 1l) == 0) {
		q1 *= q;
		if (q1 <= my_B) goto L6; else goto L5;
	}
	else
	{
		if (zcompare(zg, *zN) < 0) {
			factor.exponent = 1;
			factor.zfactor = 0;
			zcopy(zg, &factor.zfactor);
			current = insert_factor_node(first, factor);
			first = current;
			*count = *count + 1;
			zcopy(*zN, &zq1);
			zdiv(zq1, zg, zN, &zx1);
			return first;
		}

		if (zcompare(zg, *zN) == 0)
		{
			first = NULL;
		}
	}

	zfree(&zg);
	zfree(&zq1);
	zfree(&zt);
	zfree(&zx1);
	zfree(&zy);
	return first;
}

PFACTORNODE Cohen_Pollard_Method(
	verylong *zN,
	PFACTORNODE first,
	int *count)
{
	long cnt, i, *p = (long *)malloc(my_NUMBER_PRIMES * sizeof(long));
	verylong zx = 0;
	PFACTORNODE current = NULL;

	zpstart2();

	for (i = 0; i < my_NUMBER_PRIMES; i++)
		p[i] = zpnext();

	i = 0;

	int j = p[0];

	do {
		while ((current = first_stage(my_NUMBER_PRIMES, zN,
			j, p, &zx, first, &cnt)) != NULL && i < my_NUMBER_PRIMES)
		{
			i++;
			j = p[i];
			first = current;
			count += cnt;
		}
		j = p[++i];
	} while (
		!zscompare(*zN, 1l) &&
		!zprobprime(*zN, 20) &&
		i < my_NUMBER_PRIMES);

	FACTOR factor;

	factor.exponent = 1;
	factor.zfactor = *zN;
	current = insert_factor_node(first, factor);
	first = current;
	free(p);
	return first;
}

int square_test(verylong zn, verylong *zq)
{
	int square = 1;
	long q11[11], q63[63], q64[64], q65[65];
	long k, r, t;
	verylong zd = 0;

	for (k = 0; k < 11; k++) q11[k] = 0;
	for (k = 0; k < 6; k++) q11[(k * k) % 11] = 1;
	for (k = 0; k < 63; k++) q63[k] = 0;
	for (k = 0; k < 32; k++) q63[(k * k) % 63] = 1;
	for (k = 0; k < 64; k++) q64[k] = 0;
	for (k = 0; k < 32; k++) q64[(k * k) % 64] = 1;
	for (k = 0; k < 65; k++) q65[k] = 0;
	for (k = 0; k < 33; k++) q65[(k * k) % 65] = 1;
	t = zsmod(zn, 64l);
	r = zsmod(zn, 45045);
	if (q64[t] == 0) square = 0;
	if (square && q63[r % 63] == 0) square = 0;
	if (square && q65[r % 65] == 0) square = 0;
	if (square && q11[r % 11] == 0) square = 0;
	if (square) {
		zsqrt(zn, zq, &zd);
		if (zscompare(zd, 0l) != 0) square = 0;
	}

	zfree(&zd);
	return square;
}

int trial_division_1(long B, verylong *zN, verylong *zf)
{
	int e = 0;
	long p;
	verylong za = 0, zb = 0;

	zcopy(*zN, &za);
	zpstart2();
	do {
		p = zpnext();
		if (zsmod(za, p) == 0) {
			do {
				zsdiv(za, p, &zb);
				zcopy(zb, &za);
				e++;
			} while (zsmod(za, p) == 0);
			zintoz(p, zf);
			zcopy(za, zN);
		}
	} while (!e && p <= B);

	zfree(&za);
	zfree(&zb);
	return e;
}

int do_Lehman(verylong *zN, verylong *zf)
{
	long B = pow(zdoub(*zN), 1.0 / 3.0), a, k = 0, m, r;
	int e = trial_division_1(B, zN, zf);
	verylong za = 0, zb = 0, zc = 0, zh = 0, zl = 0;
	verylong zr = 0, zs = 0;

	if (!e) {
	L2:
		k++;
		if (k > B) goto L4;
		if (!(k & 1)) {
			zone(&zr);
			m = 2;
		}
		else {
			zsadd(*zN, k, &zr);
			m = 4;
		}
		zsmul(*zN, k, &za);
		zlshift(za, 2l, &zl);
		zintoz(B, &zh);
		zsq(zh, &zb);
		zadd(zl, zb, &zh);
		zsqrt(zl, &za, &zb);
		zsq(za, &zs);
		while (zcompare(zs, zl) < 0) {
			zsadd(za, 1l, &zb);
			zcopy(zb, &za);
			zsq(za, &zs);
		}
		r = zsmod(zr, m);
		while (!e && zcompare(zs, zh) <= 0) {
			a = zsmod(za, m);
			if (a == r) {
				zsub(zs, zl, &zc);
				if (zscompare(zc, 0l) == 0 || square_test(zc, &zb)) {
					zadd(za, zb, &zc);
					zgcd(zc, *zN, zf);
					do {
						zdiv(*zN, *zf, &za, &zb);
						zcopy(za, zN);
						zmod(za, *zf, &zb);
						e++;
					} while (zscompare(zb, 0l) == 0);
				}
			}
			if (!e) {
				zsadd(za, 1l, &zb);
				zcopy(zb, &za);
				zsq(za, &zs);
			}
		}
		if (!e) goto L2;
	}
L4:
	zfree(&za);
	zfree(&zb);
	zfree(&zc);
	zfree(&zh);
	zfree(&zl);
	zfree(&zr);
	zfree(&zs);
	return e;
}

PFACTORNODE Lehman(
	verylong *zN,
	PFACTORNODE first,
	int *count)
{
	int e = 0;
	verylong zf = 0;
	FACTOR factor;
	PFACTORNODE current = NULL;

	while (1)
	{
		e = do_Lehman(zN, &zf);

		if (e)
		{
			factor.exponent = e;
			factor.zfactor = 0;
			zcopy(zf, &factor.zfactor);
			current = insert_factor_node(first, factor);
			first = current;
			*count = *count + 1;
		}
		
		else if (zprobprime(*zN, 20l))
		{
			factor.exponent = 1;
			factor.zfactor = 0;
			zcopy(*zN, &factor.zfactor);
			current = insert_factor_node(first, factor);
			first = current;
			*count = *count + 1;
			break;
		}

		else
			break;
	}

	zfree(&zf);
	return first;
}

PFACTORNODE trial_division(
	verylong *zN,
	PFACTORNODE first,
	int *count)
{
	int e, one = 0, pr = 0;
	long B, p;
	verylong za = 0, zb = 0, zl = 0, zo = 0, zp = 0;
	FACTOR factor;
	PFACTORNODE current = NULL;

	zsqrt(*zN, &za, &zb);
	zone(&zo);
	zcopy(*zN, &zl);

	if (zscompare(za, my_BOUND) > 0)
		B = my_BOUND;

	else
		B = ztoint(za);

	zcopy(*zN, &za);
	zpstart2();

	do {
		p = zpnext();

		if (zsmod(za, p) == 0)
		{
			e = 0;

			do {
				zsdiv(za, p, &zb);
				zcopy(zb, &za);
				e++;
			} while (zsmod(za, p) == 0);

			zintoz(p, &zp);
			factor.exponent = e;
			factor.zfactor = 0;
			zcopy(zp, &factor.zfactor);
			current = insert_factor_node(first, factor);
			first = current;
			*count = *count + 1;
			zcopy(za, zN);
			one = zscompare(*zN, 1l) == 0;
			pr = zprobprime(*zN, 20l);

			if (!one && pr)
			{
				factor.exponent = 1;
				zcopy(*zN, &factor.zfactor);
				current = insert_factor_node(first, factor);
				first = current;
				*count = *count + 1;
				break;
			}

			else
			{
				factor.exponent = 1;
				factor.zfactor = 0;
				zcopy(*zN, &factor.zfactor);
				current = insert_factor_node(first, factor);
				first = current;
				*count = *count + 1;
			}
		}
	} while (!one && p <= B);

	PFACTORNODE last = (PFACTORNODE)malloc(sizeof(FACTORNODE));

	last->factor.exponent = 1;
	last->factor.zfactor = 0;
	zcopy(zl, &last->factor.zfactor);
	current = insert_factor_node(first, last->factor);
	first = current;
	*count = *count + 1;

	zfree(&za);
	zfree(&zb);
	zfree(&zl);
	zfree(&zo);
	zfree(&zp);
	return first;
}

int partial_addition(verylong za,
	verylong zn,
	ECPOINT P,
	ECPOINT Q,
	PECPOINT R,
	verylong *zd)

	/* returns 0 if sum is found or 1 if divisor is found */

{
	int result = -1, value = 0;
	verylong zb = 0, zc = 0, zl = 0, zs = 0;
	verylong zt = 0, zx = 0, zy = 0, zy2 = 0;

	if (zcompare(P.zx, Q.zx) == 0 &&
		zscompare(P.zy, 0l) == 0 &&
		zscompare(Q.zy, 0l) == 0) {
		zzero(&R->zx);
		zone(&R->zy);
		return 0;
	}

	zsub(zn, Q.zy, &zb);

	if (zcompare(P.zx, Q.zx) == 0 &&
		zcompare(P.zy, zb) == 0) {
		zzero(&R->zx);
		zone(&R->zy);
		return 0;
	}

	if (zscompare(P.zx, 0l) == 0 &&
		zscompare(P.zy, 1l) == 0 &&
		zscompare(P.zz, 0l) == 0) {

		/* O + Q = Q */

		zcopy(Q.zx, &R->zx);
		zcopy(Q.zy, &R->zy);
		zcopy(Q.zz, &R->zz);
		value = 0;
	}

	else if (zscompare(Q.zx, 0l) == 0 &&
		zscompare(Q.zy, 1l) == 0 &&
		zscompare(Q.zz, 0l) == 0) {

		/* P + O = P */

		zcopy(P.zx, &R->zx);
		zcopy(P.zy, &R->zy);
		zcopy(P.zz, &R->zz);
		value = 0;
	}

	else {

		/* P != O and Q != O */

		zcopy(Q.zy, &zy2);
		znegate(&zy2);
		if (zcompare(P.zx, Q.zx) == 0 &&
			zcompare(P.zy, zy2) == 0) {
			zzero(&R->zx);
			zone(&R->zy);
			zzero(&R->zz);
		}

		else {
			if (zcompare(P.zx, Q.zx) != 0) {
				zsubmod(P.zx, Q.zx, zn, &zx);
				zexteucl(zx, &zs, zn, &zt, zd);
				if (zscompare(*zd, 1l) != 0) goto L1;
				zsubmod(P.zy, Q.zy, zn, &zy);
				zmulmod(zs, zy, zn, &zl);
			}

			else {
				zaddmod(P.zy, Q.zy, zn, &zy);
				zexteucl(zy, &zs, zn, &zt, zd);
				if (zscompare(*zd, 1l) != 0) goto L1;
				zmulmod(P.zx, P.zx, zn, &zb);
				zsmulmod(zb, 3l, zn, &zc);
				zaddmod(zc, za, zn, &zb);
				zmulmod(zs, zb, zn, &zl);
			}

			zmulmod(zl, zl, zn, &zb);
			zaddmod(P.zx, Q.zx, zn, &zc);
			zsubmod(zb, zc, zn, &zx);
			zcopy(zx, &R->zx);
			zsubmod(zx, P.zx, zn, &zb);
			zmulmod(zl, zb, zn, &zc);
			zaddmod(zc, P.zy, zn, &zy);
			znegate(&zy);
			zcopy(zy, &R->zy);
			zone(&R->zz);
			goto L2;
		L1:
			value = 1;
		L2:
			;
		}
	}

	zfree(&zb);
	zfree(&zc);
	zfree(&zl);
	zfree(&zs);
	zfree(&zt);
	zfree(&zx);
	zfree(&zy);
	zfree(&zy2);
	return value;
}

int multiply(long k,
	verylong za,
	verylong zn,
	ECPOINT P,
	PECPOINT R,
	verylong *zd)
{
	int value = 0;
	ECPOINT A = { 0, 0, 0 };
	ECPOINT S = { 0, 0, 0 };
	ECPOINT T = { 0, 0, 0 };

	zone(&A.zx);
	zone(&A.zy);
	zone(&A.zz);
	zone(&S.zx);
	zone(&S.zy);
	zone(&S.zz);
	zone(&T.zx);
	zone(&T.zy);
	zone(&T.zz);

	R = (PECPOINT)malloc(sizeof(ECPOINT));

	if (R == NULL)
		exit(0);

	memset(R, 0, sizeof(ECPOINT));

	zzero(&R->zx);
	zone(&R->zy);
	zzero(&R->zz);
	zcopy(P.zx, &S.zx);
	zcopy(P.zy, &S.zy);
	zcopy(P.zz, &S.zz);

	while (!value && k != 0) {
		if (k & 1) {
			value = partial_addition(za, zn, *R, S, &A, zd);
			zcopy(A.zx, &R->zx);
			zcopy(A.zy, &R->zy);
			zcopy(A.zz, &R->zz);
		}

		k >>= 1;

		if (!value && k != 0) {
			value = partial_addition(za, zn, S, S, &T, zd);
			zcopy(T.zx, &S.zx);
			zcopy(T.zy, &S.zy);
			zcopy(T.zz, &S.zz);
		}
	}

	if (zscompare(R->zy, 0l) < 0) {
		zadd(R->zy, zn, &A.zy);
		zcopy(A.zy, &R->zy);
	}

	zfree(&A.zx);
	zfree(&A.zy);
	zfree(&A.zz);
	zfree(&S.zx);
	zfree(&S.zy);
	zfree(&S.zz);
	zfree(&T.zx);
	zfree(&T.zy);
	zfree(&T.zz);
	return value;
}

/* the following definition limits the L3 loop */

int LenstrasECM(verylong *zN, verylong *zg)
{
	int expon = 0, found;
	long B = 100000000l, i, j, k = 0, l, *p, q, q1;
	long giveUp = z2log(*zN);
	ECPOINT x, y;
	verylong za[CURVES], zb = 0, zd = 0;

	for (i = 0; i < CURVES; i++)
		za[i] = 0;

	x.zx = x.zy = x.zz = y.zx = y.zy = y.zz = 0;

	zpstart2();

	do {
		q = zpnext();
		k++;
	} while (q < B);

	p = calloc(k, sizeof(long));

	if (!p) {
		expon = -1;
		goto L4;
	}

	zpstart2();

	for (i = 0; i < k; i++)
		p[i] = zpnext();

	for (i = 0; i < CURVES; i++)
		zrandomb(*zN, &za[i]);

L2:

	zone(&x.zx);
	zone(&x.zy);
	zzero(&x.zz);
	i = -1;

L3:

	i++;

	if (i == giveUp) {
		expon = 0;
		goto L4;
	}

	if (i == k) {

		for (i = 0; i < CURVES; i++)
			zrandomb(*zN, &za[i]);

		goto L2;
	}

	q = p[i];
	q1 = q;
	l = B / q;

	while (q1 <= l)
		q1 *= q;

	found = 0;

	for (j = 0; !found && j < CURVES; j++)
		found = multiply(q1, za[j], *zN, x, &y, &zd);

	if (!found)
		goto L3;

	zcopy(y.zx, &x.zx);
	zcopy(y.zy, &x.zy);
	zcopy(y.zz, &x.zz);
	zgcd(zd, *zN, zg);

	if (zcompare(*zg, *zN) == 0) {
		for (j = 0; j < CURVES; j++)
			zrandomb(*zN, &za[j]);

		goto L2;
	}

	if (!zprobprime(*zg, 5l))
		goto L4;

	expon = 0;

	do {
		zdiv(*zN, *zg, &zb, &zd);
		zcopy(zb, zN);
		zmod(*zN, *zg, &zd);
		expon++;
	} while (zscompare(zd, 0l) == 0);

L4:

	for (i = 0; i < CURVES; i++)
		zfree(&za[i]);

	zfree(&zb);
	zfree(&zd);
	zfree(&x.zx);
	zfree(&x.zy);
	zfree(&x.zz);
	zfree(&y.zx);
	zfree(&y.zy);
	zfree(&y.zz);
	return expon;
}

PFACTORNODE CohenEllipticCurveMethod(
	char *numStr, int base, int iExpon, int addend)
{
	PFACTORNODE current, first;
	FACTOR factor;
	int result;
	int cant, expon, one, pri;
	verylong zn = 0, zN = 0, zd = 0, zg = 0;

	if (strlen(numStr) != 0)
		zstrtoz(numStr, &zN);

	else
	{
		static verylong zb = 0, zp = 0;

		zintoz(base, &zb);

		zsexp(zb, iExpon, &zp);
		zsadd(zp, addend, &zN);
	}

	zcopy(zN, &zn);

	first = insert_first_factor_node(zN, 1);

	cant = pri = 0;

	do {

		expon = LenstrasECM(&zN, &zg);

		if (expon == -1)
		{
			result = -1;
			goto L1;
		}

		if (zprobprime(zg, 20l))
		{
			factor.exponent = expon;
			factor.zfactor = zg;
			current = insert_factor_node(first, factor);
			first = current;
		}

		one = zscompare(zN, 1l) == 0;

		if (zprobprime(zN, 20l))
		{
			factor.exponent = 1;
			factor.zfactor = zN;
			current = insert_factor_node(first, factor);
			first = current;
			break;
		}

	} while (!one);

L1:

	zfree(&zn);
	zfree(&zN);
	zfree(&zd);
	zfree(&zg);

	return first;
}

PFACTORNODE LenstraEllipticCurveMethod(
	verylong *zN, PFACTORNODE first, int *count)
{
	long curvebnd = 1024, e = 0, exp = 0, phase1bnd = 64;
	long grow = 16, info = 2, nbtests = 20, s = 1;
	verylong zf = 0, zn = 0, zq = 0, zr = 0;
	FACTOR factor;
	PFACTORNODE current = NULL;

	zcopy(*zN, &zn);

	while (exp != -1)
	{
		exp = zfecm(zn, &zf, s, &curvebnd, &phase1bnd,
			grow, nbtests, info, (FILE *)NULL);

		if (exp == 1 || exp == -1)
		{
			if (zscompare(zf, 1) != 0)
			{
				*count = *count + 1;
				e = 0;
				zdiv(zn, zf, &zq, &zr);

				while (zscompare(zr, 0l) == 0)
				{
					e++;
					zcopy(zq, &zn);
					zdiv(zn, zf, &zq, &zr);
				}

				factor.exponent = e;
				factor.zfactor = zf;
				current = insert_factor_node(first, factor);
				first = current;
			}

			else
			{
				if (zprobprime(zn, 20))
				{
					factor.exponent = 1;
					factor.zfactor = zn;
					current = insert_factor_node(first, factor);
					first = current;
				}
			}
		}

		else
			break;
	}

	zfree(&zf);
	zfree(&zn);
	zfree(&zq);
	zfree(&zr);
	return first;
}
Lenstra’s Free LIP Lenstra’s ECM Factorization of the Eighth Fermat Number
Lenstra’s Free LIP Lenstra’s ECM Factorization of the Seventh Fermat Number

Blog Entry Monday April 4, 2022

This morning as I was leaving the gym at about 2:00 AM a fellow gym member made the following remark to me: “I hear you are a scientist” and I responded “yes, a computer scientist and computer or software engineer”. Later as I was headed towards my car, this same other gym member pointed towards a planet or star in the early morning sky and asked, “what is the object in the sky he was pointing towards was?”. I did note answer his question on the spot and now I offer the following theories. Well, if we had a high-resolution telescope and/or a spectroscope we could differentiate a planet from a star due to the chemical composition of the object. There is a theory posed by Alpher, Bethe, and Gamov which states the lightest elements in the universe, namely hydrogen and helium were formed during the Big Bang and the other 115 elements were either made by humans in nuclear physics laboratories (breeder nuclear reactors or other means) or the rest of the chemical elements were synthesized in the stars. Stars are classified by the Alpher, Bethe, and Gamov scheme:

Star Type Classification / NASA | Kaggle

https://blogs.scientificamerican.com/basic-space/httpblogsscientificamericancombasic-space20110802on-the-origin-of-chemical-elements/

Asymptotic giant branch – Wikipedia