The following text is based upon Appendix 5 “Higher Algebraic Number Fields” found in the book “Prime Numbers and Computer Methods for Factorization” by Hans Riesel. Cubic integers are algebraic numbers of the form [a, b, c] which is a short hand for a + b * z + c * z * z where z is the cube root of -2. we have z * z * z = z ^ 3 = -2 and z ^ 4 = -2 * z. The numbers a, b, and c are rational integers in Z. The product of two cubic integers is also a cubic integer (expansion of equation A5.8):
[a, b, c] * [d, e, f] = (a + b * z + c * z * z) * (d + e * z + f * z * z) = a * d + a * e * z + a * f * z * z + b * d * z + b * e * z * z + b * f * z * z * z + c * d * z * z + c * e * z * z * z + c * f * z * z * z * z = a * d – 2 * b * f – 2 * c * e + (a * e + b * d – 2 * c * f) * z + (a * f + b * e + c * d) * z * z = [ a * d – 2 * b * f – 2 * c * e , a * e + b * d – 2 * c * f , a * f + b * e + c * d ]
The defining equation for z is z^3 + 2 = 0. The other two roots of the polynomial f(z) = z^3 + 2 are the complex conjugates z[2] = z * (-1 + i * SQR(3)) / 2 and z[3] = z * (-1 – i * SQR(3)) / 2, where SQR(x) is the square root function such that x = SQR(x) * SQR(x) and i = SQR(-1), the imaginary unit. z[2] and z[3] are complex numbers of the form w = u + i * v, where u is the real part and v is the imaginary part. Let o = (-1 + i * SQR(3)) / 2. z[2] = o * z and z[3] = o * o * z.
Q(z) is a field and the integers of the field form Z(z) which is a ring. The norm of the cubic integer [a, b, c] is (expansion of equation A5.7):
N[a, b, c] = (a + b * z + c * z * z) * (a + b * o * z + c * o * o * z * z) * (a + b * o * o * z + c * o * z * z) = a ^ 3 – 2b ^ 3 + 4 * c ^ 3 + 6 * a * b * c
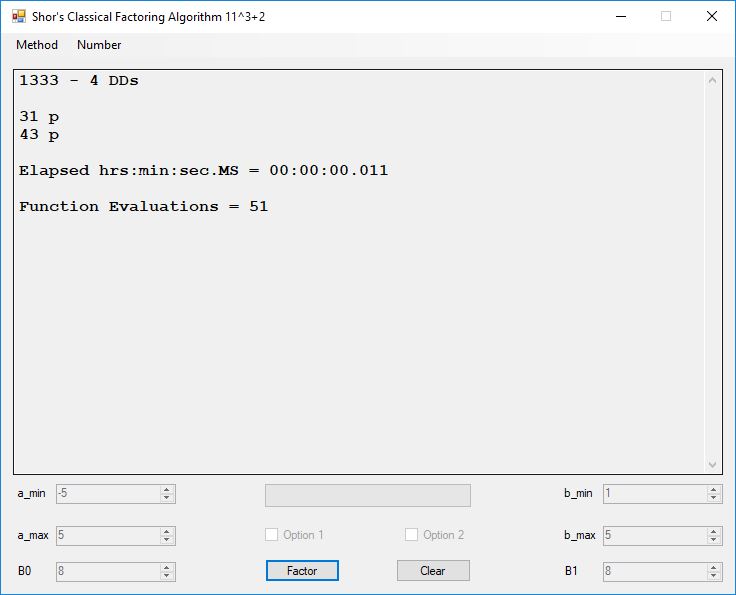
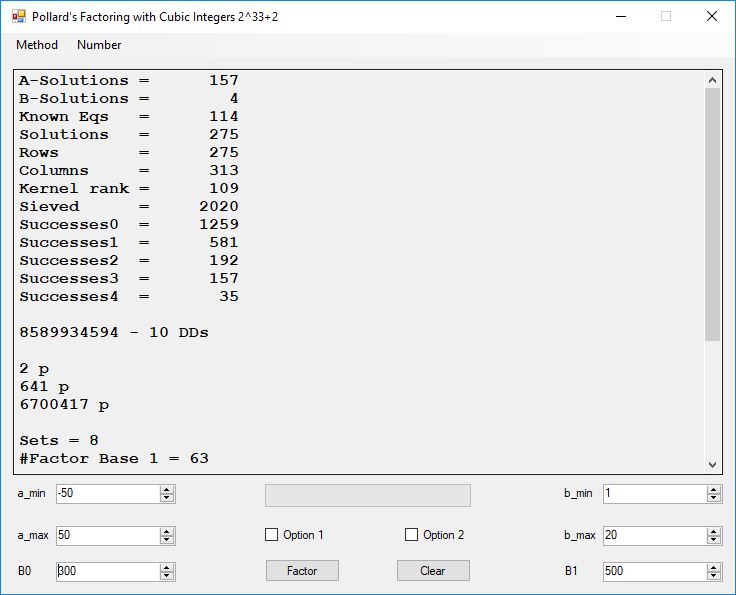
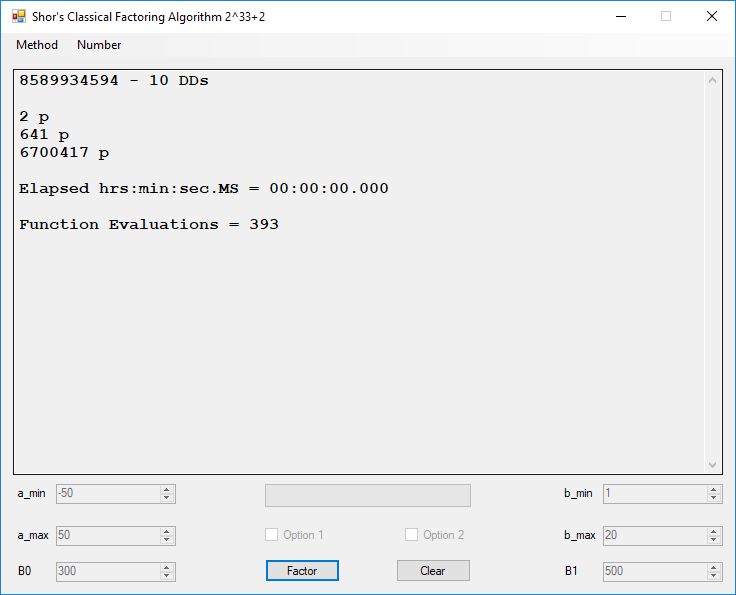
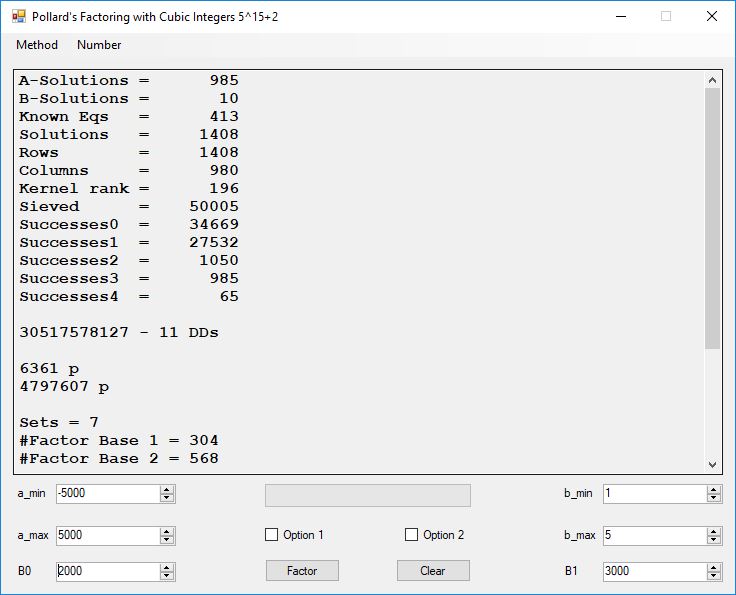
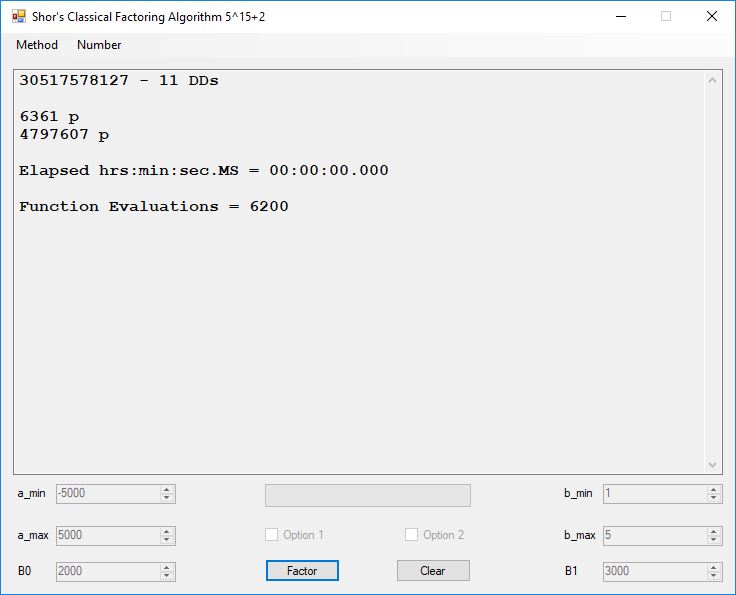
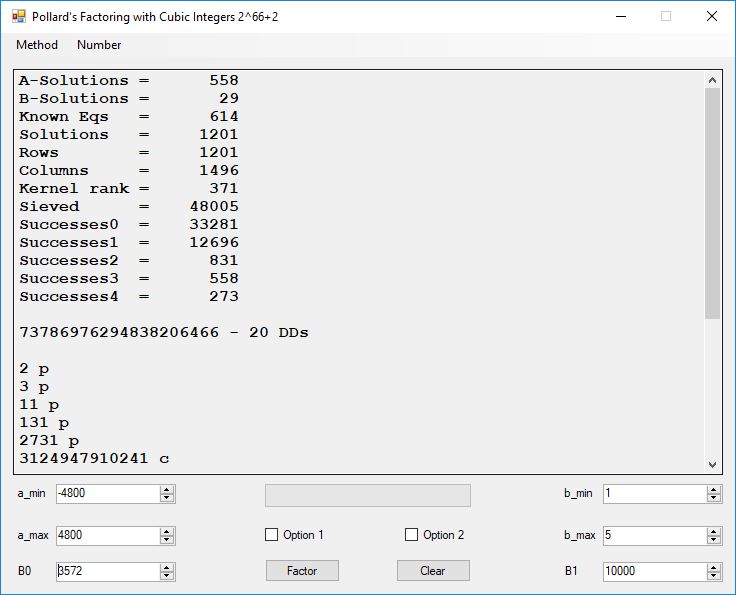
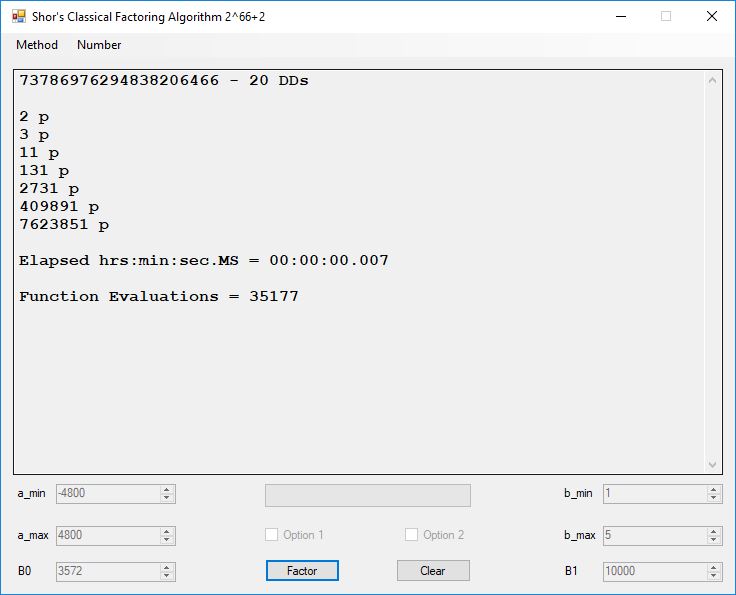
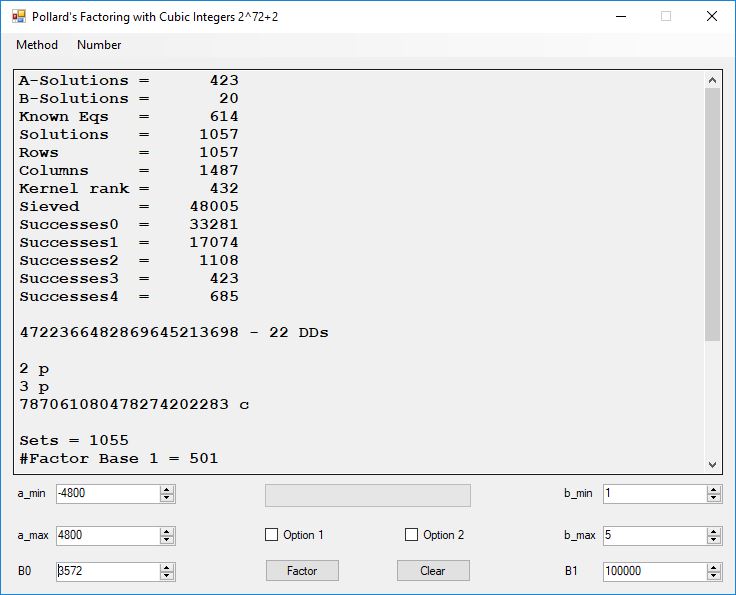
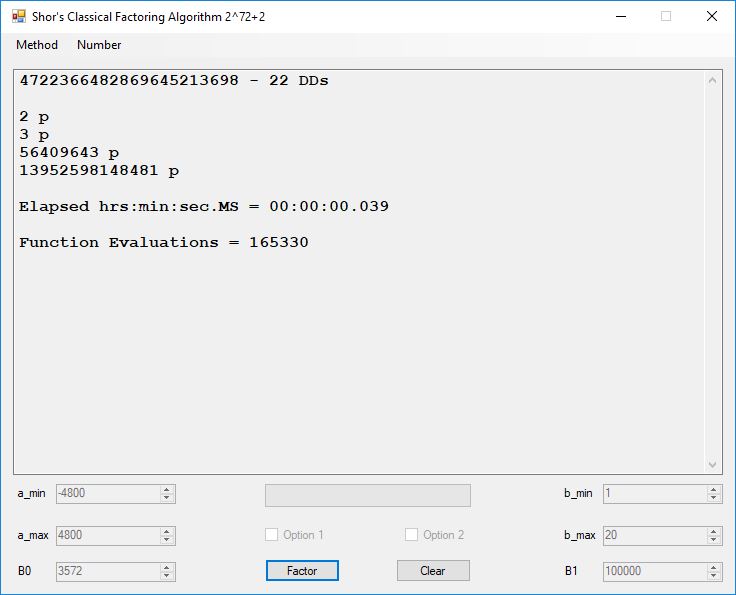
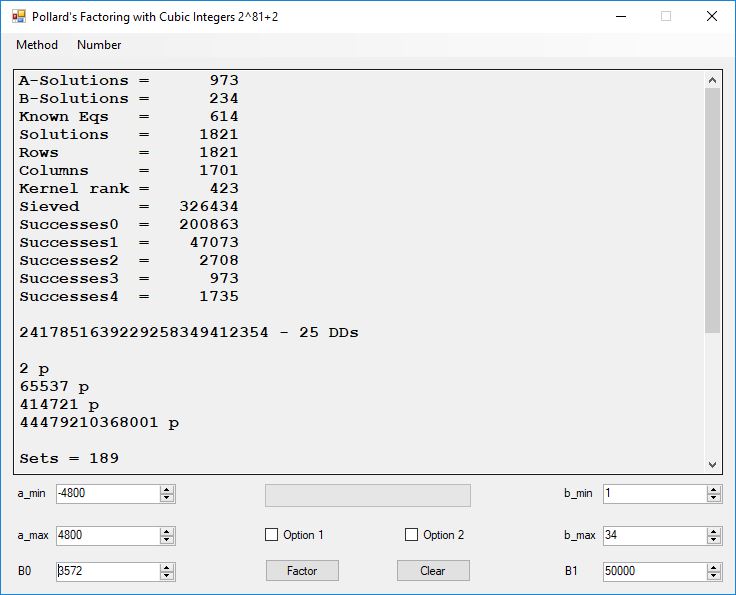
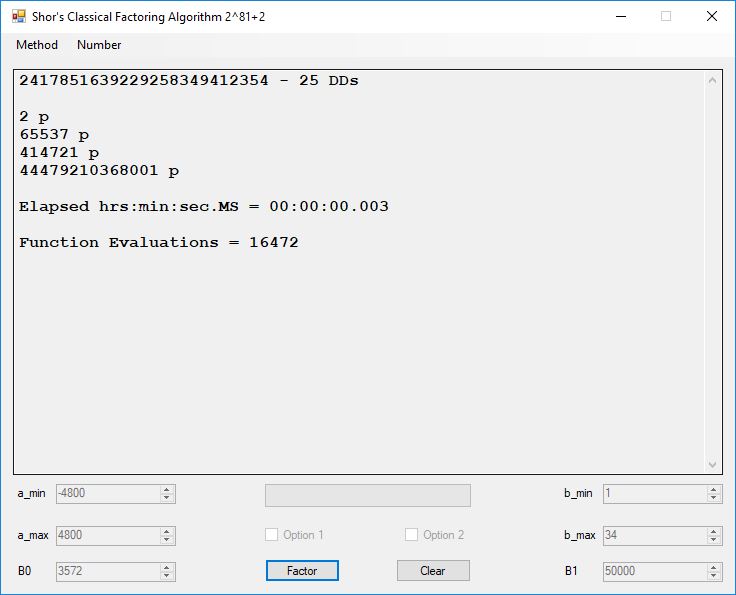
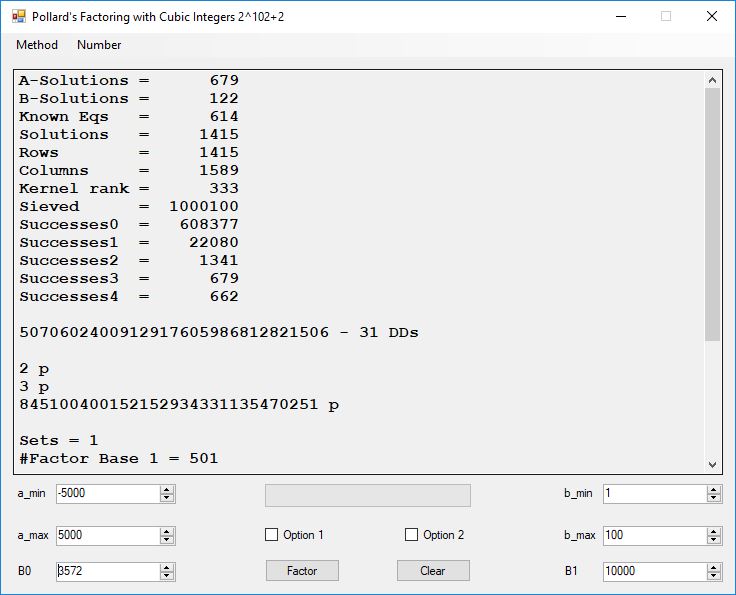
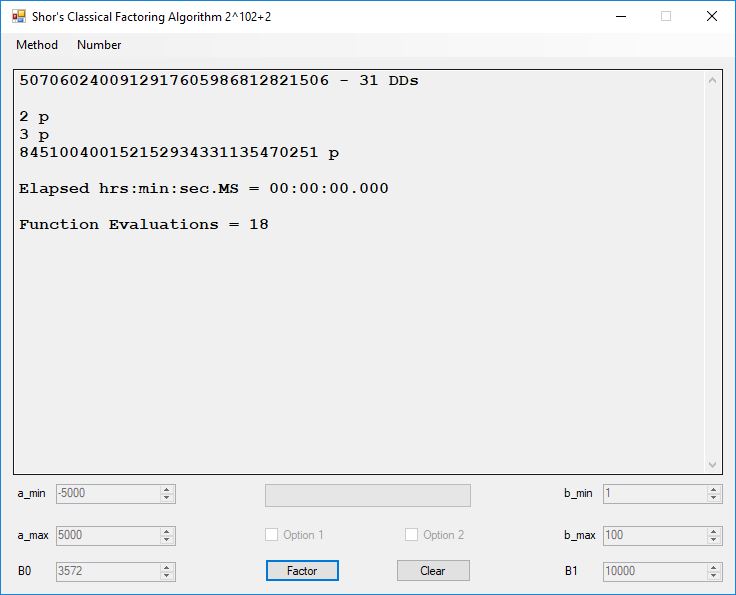
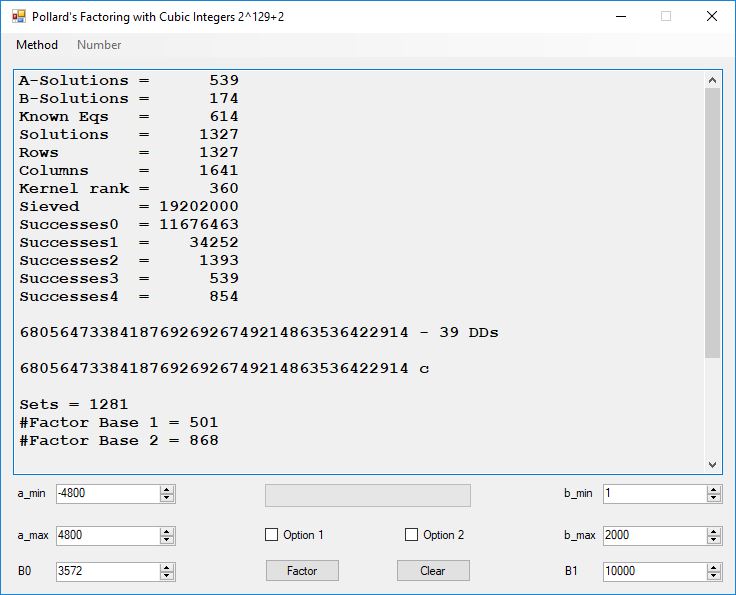
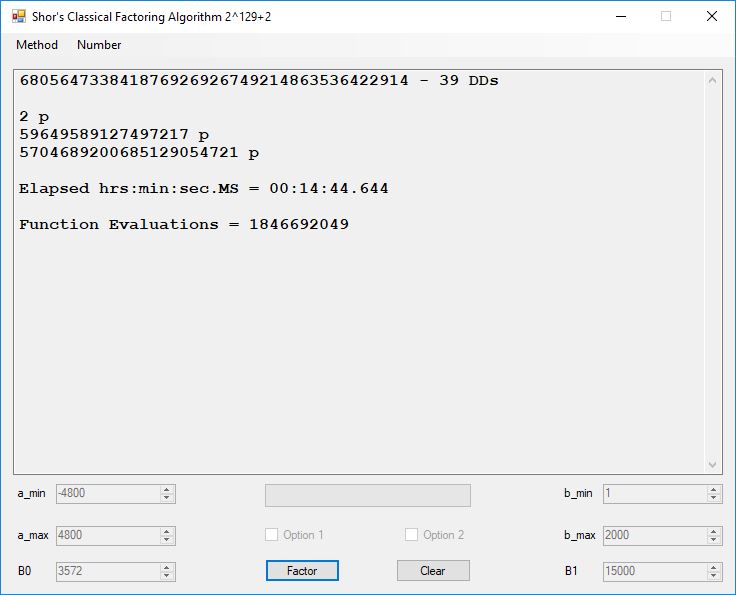
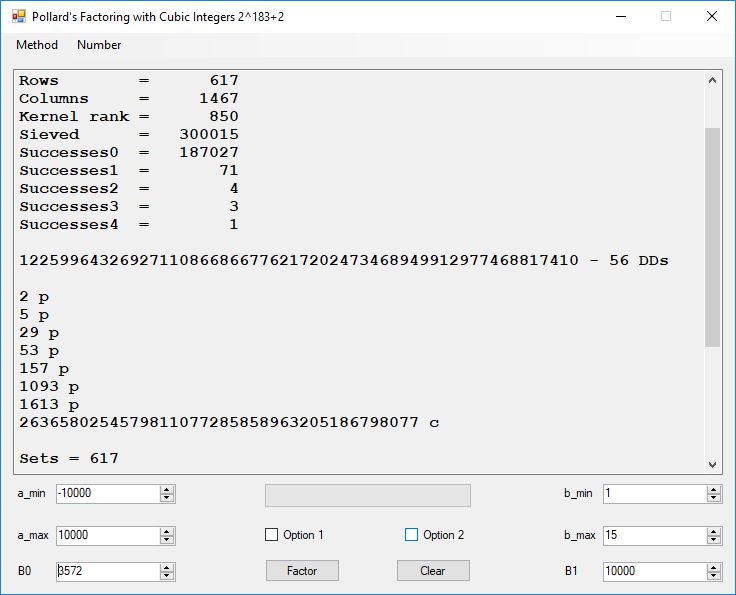
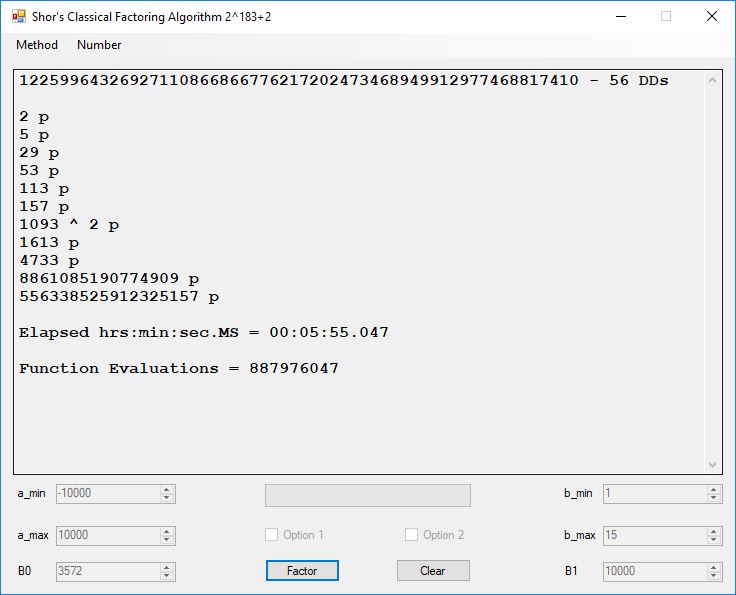
I wrote a computer application in C# to recreate the results of Appendix 5. Below is a screen shot of the application’s form:
I reproduce the units table of page 300 below:
Positive Units
[ 1, 0, 0, 1] 1
[ 1, 1, 0, 1] -1
[ 1, 2, 1, 1] 1
[ -1, 3, 3, 1] -1
[ -7, 2, 6, 1] 1
[ -19, -5, 8, 1] -1
[ -35, -24, 3, 1] 1
[ -41, -59, -21, 1] -1
[ 1, -100, -80, 1] 1
[ 161, -99, -180, 1] -1
[ 521, 62, -279, 1] 1
[ 1079, 583, -217, 1] -1
[ 1513, 1662, 366, 1] 1
Negative Units
[ -1, 0, 0, -1] -1
[ -1, 1, -1, -1] -1
[ 5, -4, 3, -1] 1
[ -19, 15, -12, -1] -1
[ 73, -58, 46, -1] 1
[ -281, 223, -177, -1] -1
[ 1081, -858, 681, -1] 1
[ -4159, 3301, -2620, -1] -1
[ 16001, -12700, 10080, -1] 1
[ -61561, 48861, -38781, -1] -1
[ 236845, -187984, 149203, -1] 1
[ -911219, 723235, -574032, -1] -1
[ 3505753, -2782518, 2208486, -1] 1
The pertinent factorization of the cubic integer prime numbers less than 300 are given next:
Case 1
[ 1, 0, 1, 5] 5
[ -1, -1, 1, 11] 11
[ 1, -2, 0, 17] 17
[ 3, 0, -1, 23] 23
[ 3, -1, 0, 29] 29
[ 1, -3, 1, 41] 41
[ 3, 1, 1, 47] 47
[ -1, -3, 0, 53] 53
[ 3, 0, 2, 59] 59
[ -1, -2, 2, 71] 71
[ 3, -2, -2, 83] 83
[ 1, -2, 3, 89] 89
[ -3, -4, 0, 101] 101
[ -1, 0, 3, 107] 107
[ 1, -4, 2, 113] 113
[ 3, -3, -1, 131] 131
[ -3, -1, 3, 137] 137
[ 1, -4, -1, 149] 149
[ -3, -3, 2, 167] 167
[ 3, -5, 4, 173] 173
[ 5, -3, 0, 179] 179
[ -1, 2, 4, 191] 191
[ 5, -2, -1, 197] 197
[ 3, 2, 3, 227] 227
[ 5, 0, 3, 233] 233
[ 1, -3, 4, 239] 239
[ 1, -5, 0, 251] 251
[ 1, 0, 4, 257] 257
[ 3, -4, -3, 263] 263
[ 1, -5, 3, 269] 269
[ -1, -1, 4, 281] 281
[ -3, -6, -1, 293] 293
Case 2
[ -1, 0, 2, 31] 31
[ 3, 0, 1, 31] 31
[ -1, -2, 1, 31] 31
[ 1, 1, 2, 43] 43
[ 3, -1, -1, 43] 43
[ 3, -2, 0, 43] 43
[ 1, 0, 3, 109] 109
[ 1, -4, 1, 109] 109
[ 5, 2, 0, 109] 109
[ -1, -4, 0, 127] 127
[ -1, -1, 3, 127] 127
[ 5, -1, 0, 127] 127
[ 5, 1, 1, 157] 157
[ 5, 0, 2, 157] 157
[ 3, -3, -2, 157] 157
[ 3, -4, -1, 223] 223
[ -3, -5, 0, 223] 223
[ 1, -5, 2, 223] 223
[ -1, 1, 4, 229] 229
[ -3, 0, 4, 229] 229
[ 5, -2, -2, 229] 229
[ 1, -5, -1, 277] 277
[ 3, -5, 0, 277] 277
[ -3, -4, 2, 277] 277
[ -1, -5, 1, 283] 283
[ 3, 0, 4, 283] 283
[ 5, 3, 2, 283] 283
Case 3
[ 0, 1, 0, 2] -2
Case 4
[ -1, 1, 0, 3] -3
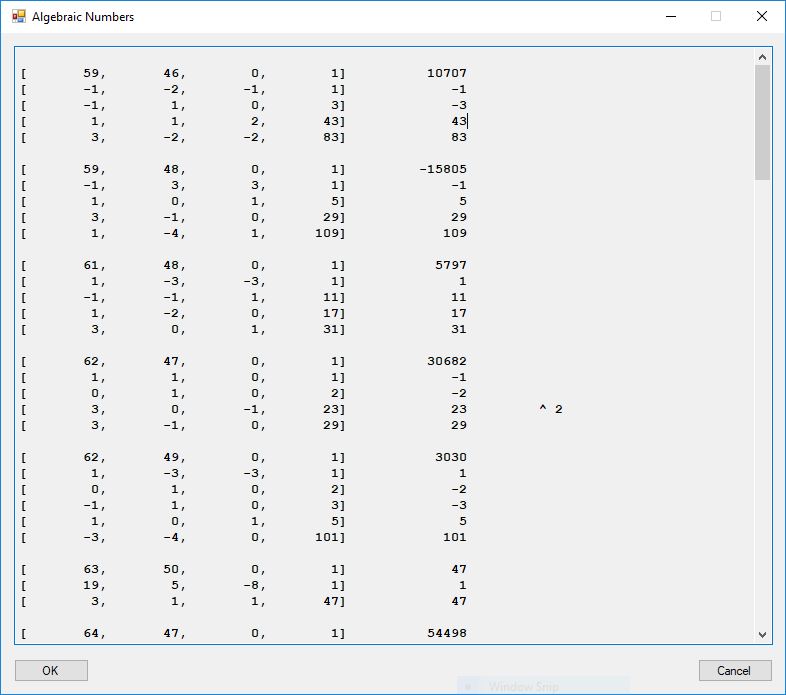
I reproduce the factorization of the norms of [a, b, 0] found on page 303 are given below:
[ 59, 46, 0, 1] 10707
[ -1, -2, -1, 1] -1
[ -1, 1, 0, 3] -3
[ 1, 1, 2, 43] 43
[ 3, -2, -2, 83] 83
[ 59, 48, 0, 1] -15805
[ -1, 3, 3, 1] -1
[ 1, 0, 1, 5] 5
[ 3, -1, 0, 29] 29
[ 1, -4, 1, 109] 109
[ 61, 48, 0, 1] 5797
[ 1, -3, -3, 1] 1
[ -1, -1, 1, 11] 11
[ 1, -2, 0, 17] 17
[ 3, 0, 1, 31] 31
[ 62, 47, 0, 1] 30682
[ 1, 1, 0, 1] -1
[ 0, 1, 0, 2] -2
[ 3, 0, -1, 23] 23 ^ 2
[ 3, -1, 0, 29] 29
[ 62, 49, 0, 1] 3030
[ 1, -3, -3, 1] 1
[ 0, 1, 0, 2] -2
[ -1, 1, 0, 3] -3
[ 1, 0, 1, 5] 5
[ -3, -4, 0, 101] 101
[ 63, 50, 0, 1] 47
[ 19, 5, -8, 1] 1
[ 3, 1, 1, 47] 47
[ 64, 47, 0, 1] 54498
[ -1, -1, 0, 1] 1
[ 0, 1, 0, 2] -2
[ -1, 1, 0, 3] -3
[ -1, 0, 2, 31] 31
[ -3, -6, -1, 293] 293
[ 65, 53, 0, 1] -23129
[ 1, 1, 0, 1] -1
[ -3, -4, 0, 101] 101
[ -3, 0, 4, 229] 229
[ 66, 53, 0, 1] -10258
[ 1, 2, 1, 1] 1
[ 0, 1, 0, 2] -2
[ 3, 0, -1, 23] 23
[ 3, -4, -1, 223] 223
[ 67, 53, 0, 1] 3009
[ 7, -2, -6, 1] -1
[ -1, 1, 0, 3] -3
[ 1, -2, 0, 17] 17
[ 3, 0, 2, 59] 59
[ 1693, 749, 0, 1] 4012180059
[ -1, -2, -1, 1] -1
[ -1, 1, 0, 3] -3
[ 3, -2, 0, 43] 43
[ 5, 0, 2, 157] 157
[ 7, -3, 0, 397] 397
[ 5, 1, 4, 499] 499
The last factorization is from “The Development of the Number Field Sieve” edited by A. K. Lenstra and H. W. Lenstra, Jr. containing the paper “Factoring with Cubic Integers” by J. M. Pollard page 10.