Shor’s algorithm is a fast method of factoring integers using a quantum computer:
https://en.wikipedia.org/wiki/Shor%27s_algorithm
I have implemented the algorithm classically and performed a few experiments on integers greater than equal 12. I used Floyd’s cycle finding algorithm as implemented with a randomized Pollard’s Rho Factoring method using two second degree polynomials:
https://en.wikipedia.org/wiki/Pollard%27s_rho_algorithm
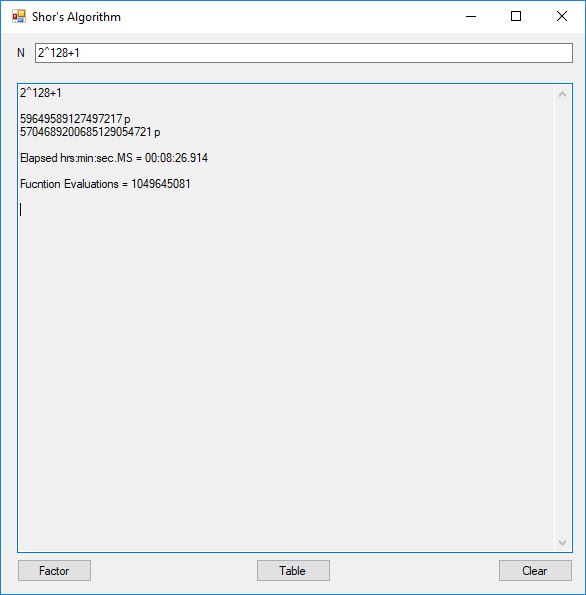
I factored the seventh Fermat number in less than nine minutes. J. M. Pollard factored this number in 20.1 hours in 1988 using the special number field sieve [see “Lecture Notes in Mathematics 1554 The Development of the Number Field Sieve” edited by A. K. Lenstra and H. W. Lenstra, Jr. The paper by Pollard is entitled “Factoring with Cubic Integers”]. Both Pollard and I used personal computers.
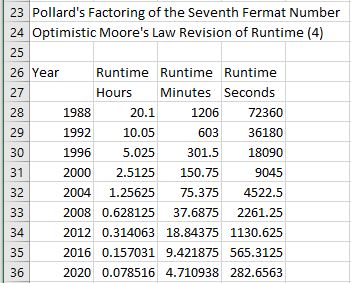
Suppose Moore’s original law is applied to Pollard’s factoring of the seventh Fermat number and also assume computing time is cut in half every two years then we can compute the following table:

A less optimistic table states that the computation time is halved every four years:
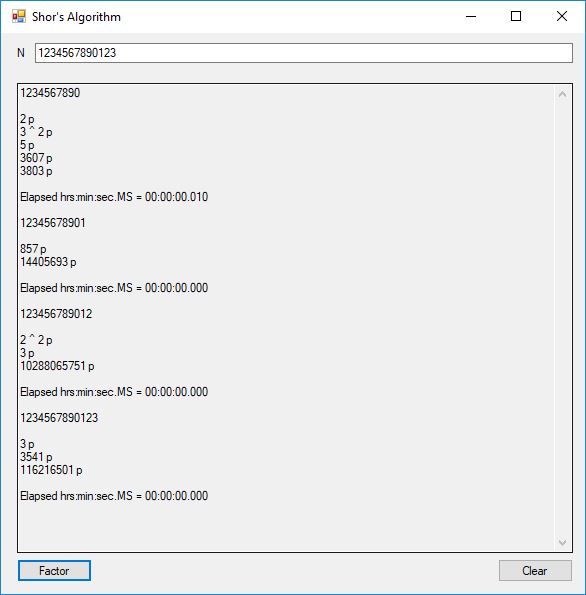
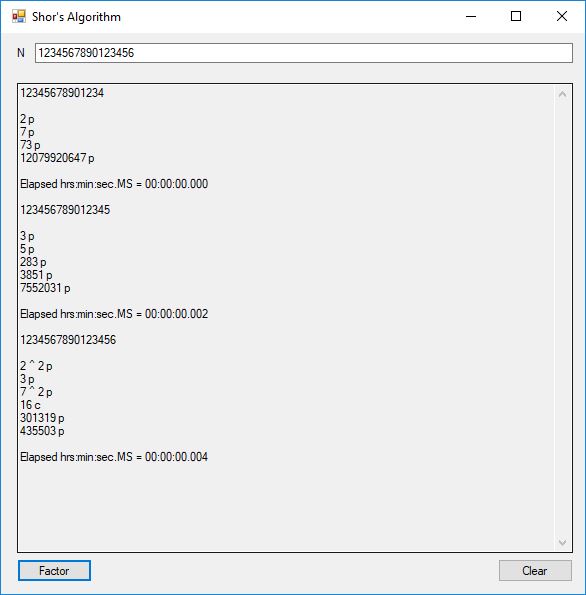
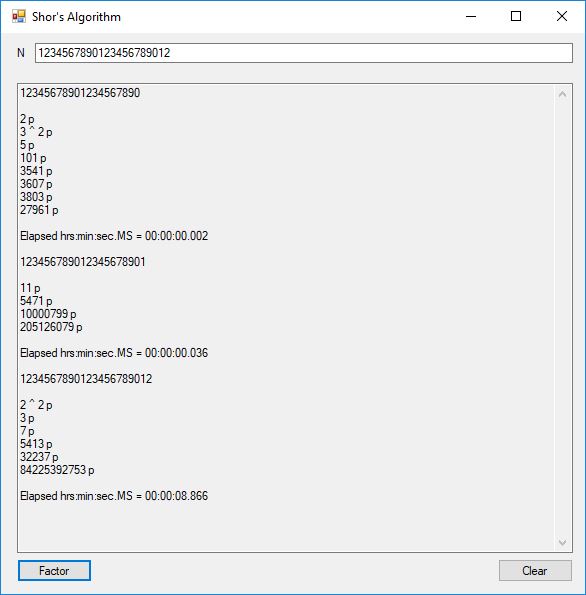
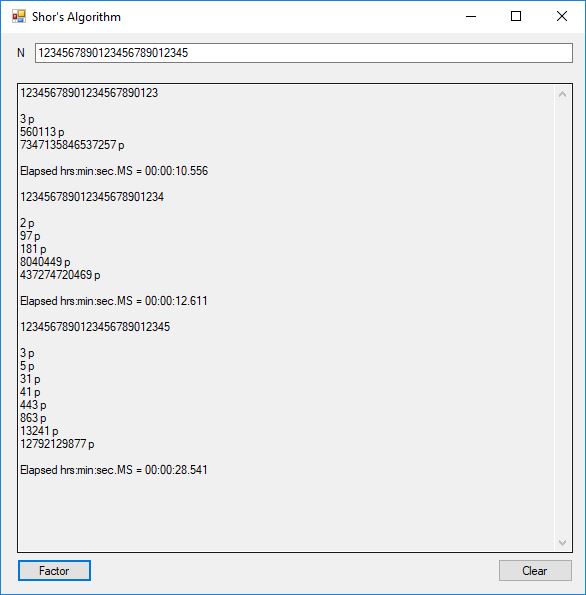
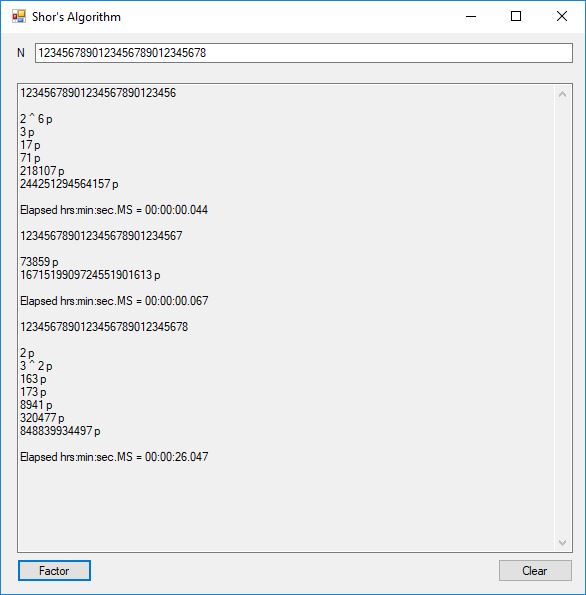
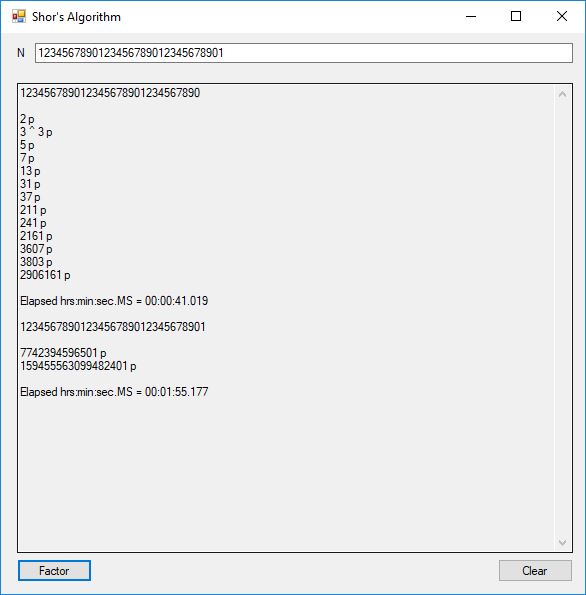
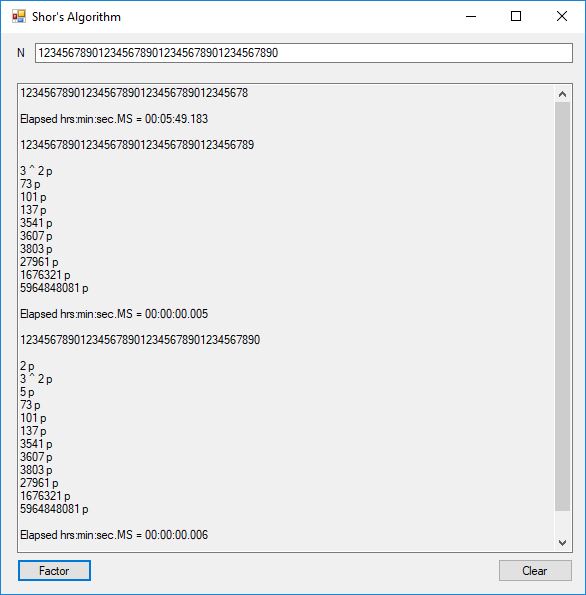
I successfully factored 38 of 39 numbers of the form 12, 123, 1234, 12345, … , 1234567890123456789012345678901234567890. The results of my factoring C# Windows form application are displayed below:
I was eventually able to factor the 38-decimal digit number that failed in the above calculation as illustrated below:
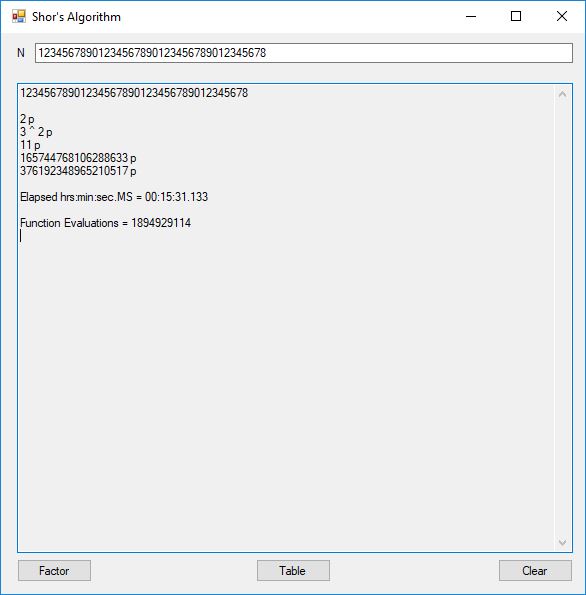
The number of bits per number varied from 4-bits to 130-bits. This is still no where near the ability to factor a 3,000-bit Rivest-Shamir-Adleman composite integer so most financial systems remain secure. The link below will take you to the Microsoft C# project directory on my OneDrive account.
https://1drv.ms/f/s!AjoNe9CiN2M9gfMbQ8H_g3GMQEC6iA
The C# source code is at the preceding link in a printable and readable PDF.