Category: Elementary Physics
New and Corrected Ground State Energy Numerical Computation for the Helium Like Atom (Atomic Number 2) by James Pate Williams, Jr.
A New Calculus of Variations Solution of the Schrödinger Equation for the Lithium Like Atom’s Ground State Energy
This computation took a lot longer time to reach a much better solution than my previously published result.
Guitar String and Piano Key Frequencies by James Pate Williams, Jr.
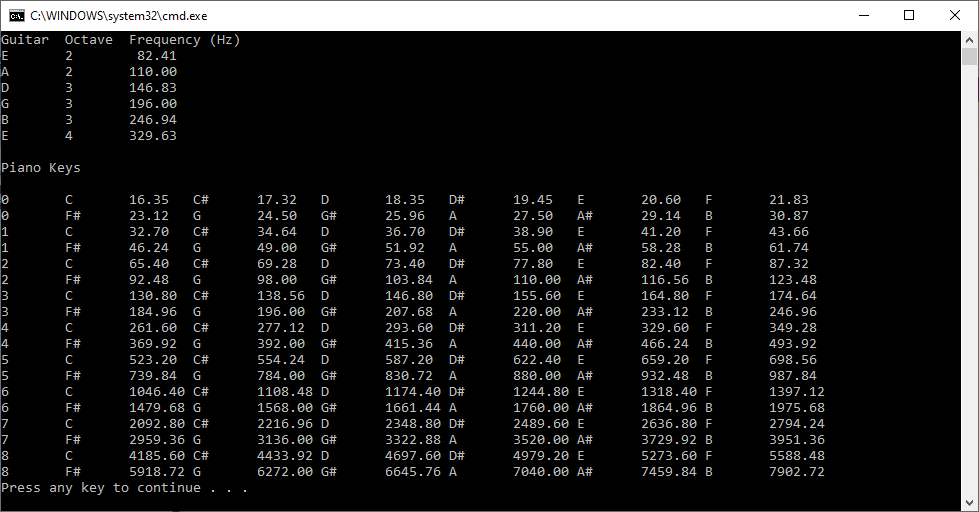
// FrequencyKey.cpp : Defines the entry point for the console application.
// James Pate Willims, Jr. (c) All Applicable Rights Reserved
#include "stdafx.h"
#include <math.h>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<string> pnote;
double a = pow(2.0, 1.0 / 12.0);
double f0 = 440.0, gStrF[6];
double e2, a2, d3, g3, b3, e4;
double pfreq[9 * 12];
int offset = 0;
double fn(int n)
{
return f0 * pow(a, n);
}
void printFrequency(char note, int octave, double frequency)
{
cout << note << "\t" << octave << "\t";
cout << setw(6) << fixed << setprecision(2);
cout << frequency << endl;
}
int main()
{
for (int octave = 0; octave <= 8; octave++)
{
pnote.push_back("C");
pnote.push_back("C#");
pnote.push_back("D");
pnote.push_back("D#");
pnote.push_back("E");
pnote.push_back("F");
pnote.push_back("F#");
pnote.push_back("G");
pnote.push_back("G#");
pnote.push_back("A");
pnote.push_back("A#");
pnote.push_back("B");
}
pfreq[0] = 16.35;
pfreq[1] = 17.32;
pfreq[2] = 18.35;
pfreq[3] = 19.45;
pfreq[4] = 20.6;
pfreq[5] = 21.83;
pfreq[6] = 23.12;
pfreq[7] = 24.5;
pfreq[8] = 25.96;
pfreq[9] = 27.5;
pfreq[10] = 29.14;
pfreq[11] = 30.87;
for (int octave = 1; octave <= 8; octave++)
{
for (int i = 0; i < 12; i++)
{
pfreq[octave * 12 + i] = 2.0 * pfreq[(octave - 1) * 12 + i];
}
}
gStrF[0] = e2 = fn(offset - 29);
gStrF[1] = a2 = fn(offset - 24);
gStrF[2] = d3 = fn(offset - 19);
gStrF[3] = g3 = fn(offset - 14);
gStrF[4] = b3 = fn(offset - 10);
gStrF[5] = e4 = fn(offset - 5);
cout << "Guitar\tOctave\tFrequency (Hz)" << endl;
printFrequency('E', 2, e2);
printFrequency('A', 2, a2);
printFrequency('D', 3, d3);
printFrequency('G', 3, g3);
printFrequency('B', 3, b3);
printFrequency('E', 4, e4);
cout << endl;
cout << "Piano Keys" << endl << endl;
for (int octave = 0; octave <= 8; octave++)
{
for (int i = 0; i < 2; i++)
{
cout << octave << '\t';
for (int j = 0; j < 6; j++)
{
{
cout << pnote[(12 * octave + 6 * i + j) % 12] << '\t';
cout << pfreq[(12 * octave + 6 * i + j)] << '\t';
}
}
cout << endl;
}
}
return 0;
}
Two of Kepler’s Three Laws of Planetary Motion by James Pate Williams, Jr.
Derivation of de Broglie’s Wave-Particle Duality Principle of Quantum Mechanics and Macroscopic Exercise by James Pate Williams, Jr.
Estimated Babe Ruth 1921 Homerun Parameters by James Pate Williams, Jr.
“Babe Ruth is generally considered the owner of the record for the longest home run in MLB history with a 575-foot bomb launched at Navin Field in Detroit in 1921.” – https://www.msn.com/en-us/sports/mlb/what-is-the-longest-home-run-in-mlb-history/ar-AA1dGwlZ
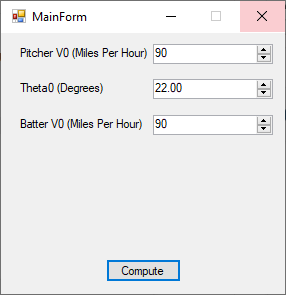
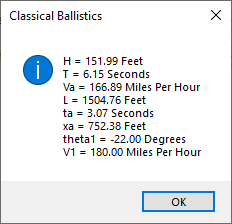
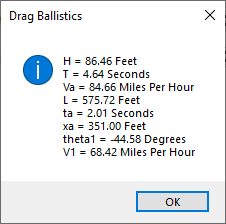
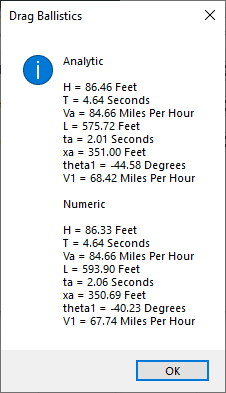
As you can see, I estimated the pitch velocity at 90 miles per hour and Babe Ruth’s (Sultan of Swing) at 90 miles per hour also. My analytic calculations yield a range of the baseball’s trajectory as about 576 feet.
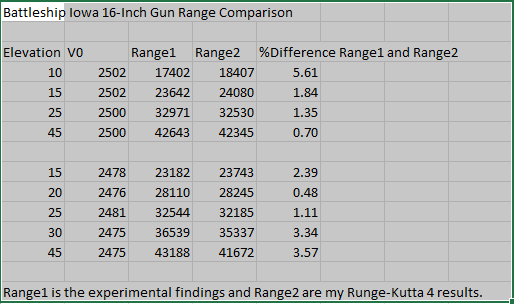
Another Point-Mass Ballistics Application Battleship Iowa 16-Inch Guns in Particular
by James Pate Williams, Jr.
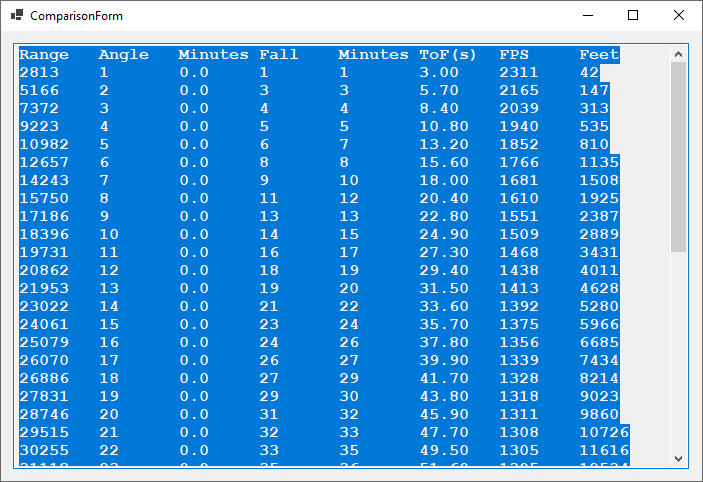
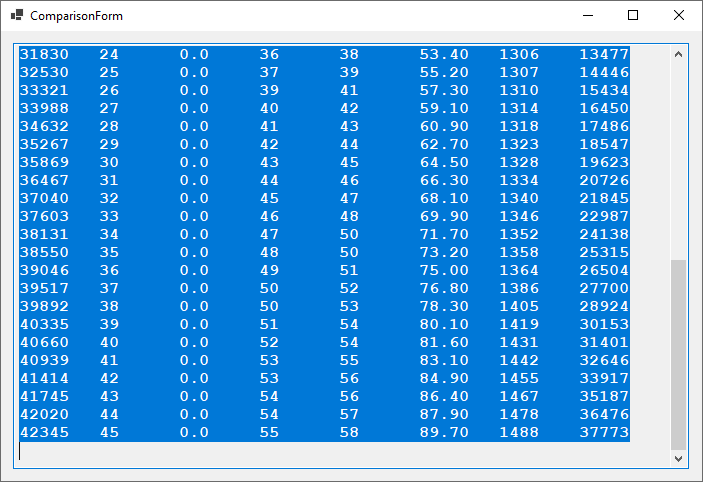
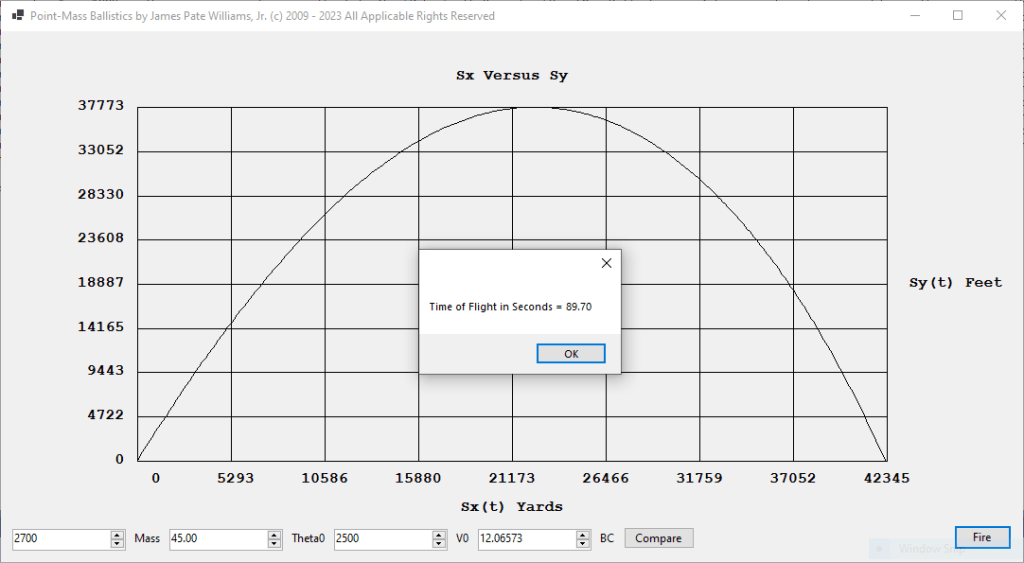
namespace PointMassBallistics
{
public class TableEntry : IComparable<TableEntry>
{
public double range, elevationDegrees, elevationMinutes,
angleFallDegrees, angleFallMinutes, timeOfFlight,
strikingVelocity, maximumOrdinate;
public int CompareTo(TableEntry other)
{
if (elevationDegrees < other.elevationDegrees &&
elevationMinutes < other.elevationMinutes)
return -1;
if (elevationDegrees > other.elevationDegrees &&
elevationMinutes > other.elevationMinutes)
return +1;
return 0;
}
}
}
// Solves the following system of first order
// ordinary differential equations. Formulas
// are from "Elementary Numerical Analysis:
// An Algorithmic Approach 3rd Edition" by S.
// D. Conte & Carl de Boor (c) 1980 8.12 page 398.
// Extended from two to four equations.
// See https://apps.dtic.mil/dtic/tr/fulltext/u2/a439796.pdf
// Also view https://eugeneleeslover.com/USN-GUNS-AND-RANGE-TABLES/OP-770-1.html
using System;
using System.Collections.Generic;
namespace PointMassBallistics
{
class RungeKutta4
{
private double BC;
private readonly double g = 32.17405;
private readonly double[] GarveN = {
2, 3, 5, 3, 2, 1.7, 1.55 };
private readonly double[] log10K = {
5.66989 - 10, 2.77344 - 10, 6.80187 - 20,
2.98090 - 10, 6.11926 - 10, 7.09620 - 10, 7.60905 - 10 };
private readonly double[] K = new double[7];
private int zone;
static private double Density(double y)
{
return Math.Pow(10, -0.00001372 * y);
}
static private int ComputeIndex(double v)
{
int index;
if (v > 3600)
index = 6;
else if (v > 2600 && v <= 3600)
index = 5;
else if (v > 1800 && v <= 2600)
index = 4;
else if (v > 1370 && v <= 1800)
index = 3;
else if (v > 1230 && v <= 1370)
index = 2;
else if (v > 790 && v <= 1230)
index = 1;
else
index = 0;
return index;
}
public double MayevskiRetardation(double v, int zone)
{
// See Exterior Ballistics 1935 by Ernest Edward Herrmann
// Garve function
return K[zone] * Math.Pow(v, GarveN[zone]);
}
private double Vx(double syn, double vxn, double vyn)
{
double v = Math.Sqrt(vxn * vxn + vyn * vyn);
zone = ComputeIndex(v);
double E = Density(syn) * MayevskiRetardation(v, zone) / BC;
return -E * vxn / v;
}
private double Vy(double syn, double vxn, double vyn)
{
double v = Math.Sqrt(vxn * vxn + vyn * vyn);
zone = ComputeIndex(v);
double E = Density(syn) * MayevskiRetardation(v, zone) / BC;
return -E * vyn / v - g;
}
static private double Sx(double vxn)
{
return vxn;
}
static private double Sy(double vyn)
{
return vyn;
}
public void Solve(
double t0, double t1,
double vx0, double vy0,
double sx0, double sy0,
double BC, int nSteps, ref List<double> lt,
ref List<double> lvx, ref List<double> lvy,
ref List<double> lsx, ref List<double> lsy)
{
double k1, k2, k3, k4;
double l1, l2, l3, l4;
double m1, m2, m3, m4;
double n1, n2, n3, n4;
double h = (t1 - t0) / nSteps, tn = t0;
double vxn = vx0, vyn = vy0, sxn = sx0, syn = sy0;
int n = 1;
for (int i = 0; i < log10K.Length; i++)
K[i] = Math.Pow(10, log10K[i]);
this.BC = BC;
lt.Add(tn);
lvx.Add(vxn);
lvy.Add(vyn);
lsx.Add(sxn / 3);
lsy.Add(syn);
while (true)
{
tn = t0 + n * h;
k1 = h * Vx(syn, vxn, vyn);
l1 = h * Vy(syn, vxn, vyn);
m1 = h * Sx(vxn);
n1 = h * Sy(vyn);
k2 = h * Vx(syn + 0.5 * n1, vxn + 0.5 * k1, vyn + 0.5 * l1);
l2 = h * Vy(syn + 0.5 * n1, vxn + 0.5 * k1, vyn + 0.5 * l1);
m2 = h * Sx(vxn + 0.5 * m1);
n2 = h * Sy(vyn + 0.5 * n1);
k3 = h * Vx(syn + 0.5 * n2, vxn + 0.5 * k2, vyn + 0.5 * l2);
l3 = h * Vy(syn + 0.5 * n2, vxn + 0.5 * k2, vyn + 0.5 * l2);
m3 = h * Sx(vxn + 0.5 * m2);
n3 = h * Sy(vyn + 0.5 * n2);
k4 = h * Vx(syn + n3, vxn + k3, vyn + l3);
l4 = h * Vy(syn + n3, vxn + k3, vyn + l3);
m4 = h * Sx(vxn + m3);
n4 = h * Sy(vyn + n3);
vxn = vx0 + (k1 + 2 * k2 + 2 * k3 + k4) / 6.0;
vyn = vy0 + (l1 + 2 * l2 + 2 * l3 + l4) / 6.0;
sxn = sx0 + (m1 + 2 * m2 + 2 * m3 + m4) / 6.0;
syn = sy0 + (n1 + 2 * n2 + 2 * n3 + n4) / 6.0;
vx0 = vxn;
vy0 = vyn;
sx0 = sxn;
sy0 = syn;
n++;
lt.Add(tn);
lvx.Add(vxn);
lvy.Add(vyn);
lsx.Add(sxn / 3);
lsy.Add(syn);
if (syn <= 1.0e-2)
break;
}
}
}
}
The Laplace Equation in Various Orthogonal Rectilinear Coordinate Systems James Pate Williams, Jr. BA, BS, MSwE, PhD
Solve the Laplace equation in the following orthogonal rectilinear coordinate systems:
- Cartesian coordinates
- Cylindrical coordinates
- Spherical polar coordinates
- Parabolic cylindrical coordinates
Solution PDF:
Selected Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 27 Quantum Behavior: Waves, Particles, and Photons – Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD
Computerized solutions to Exercises 27.3 to 27.6:
Partial source code for the preceding C# application:
Detailed solutions to Exercises 27.3 to 27.7 in a Portable Document File (PDF):
Numerical Explorations 