Category: Handbook of Applied Cryptography
Blog Entry © Tuesday, October 21, 2025, by James Pate Williams, Jr., Solving Low Density Subset Sum Problems Using the LLL-Lattice Reduction Algorithm
// Algorithm found in the "Handbook of
// Applied Cryptography" (c) 1997 by
// Alfred J. Menezes, Paul C van Oorschot,
// and Scott Vanstone 3.105 Algorithm
// Chapter 3 pages 120 - 121
#pragma once
class LLL_Lattice
{
private:
static double Scalar(
int n,
std::vector<double> u,
std::vector<double> v);
static void RED(
int k, int l, int n,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& h,
std::vector<std::vector<double>>& mu);
static void SWAP(
int k, int k1, int kmax, int n,
double m, std::vector<double>& B,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& bs,
std::vector<std::vector<double>>& h,
std::vector<std::vector<double>>& mu);
public:
static bool LLL(
int n,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& h);
};
#include "pch.h"
#include "LLL_Lattice.h"
double LLL_Lattice::Scalar(
int n,
std::vector<double> u,
std::vector<double> v)
{
// Calculate the scalar product of two vectors [1..n]
double sum = 0.0;
for (int i = 1; i <= n; i++) sum += u[i] * v[i];
return sum;
}
void LLL_Lattice::RED(
int k, int l, int n,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& h,
std::vector<std::vector<double>>& mu)
{
int i, q = (int)(0.5 + mu[k][l]);
if (fabs(mu[k][l]) > 0.5)
{
for (i = 1; i <= n; i++)
{
b[k][i] -= q * b[l][i];
h[i][k] -= q * h[i][l];
}
mu[k][l] -= q;
for (i = 1; i <= l - 1; i++)
{
mu[k][i] -= q * mu[l][i];
}
}
}
void LLL_Lattice::SWAP(
int k, int k1, int kmax, int n,
double m, std::vector<double>& B,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& bs,
std::vector<std::vector<double>>& h,
std::vector<std::vector<double>>& mu)
{
double C, t;
int i, j;
std::vector<double> c(n + 1);
for (j = 1; j <= n; j++)
{
t = b[k][j];
b[k][j] = b[k1][j];
b[k1][j] = t;
t = h[j][k];
h[j][k] = h[j][k1];
h[j][k1] = t;
}
if (k > 2)
{
for (j = 1; j <= k - 2; j++)
{
t = mu[k][j];
mu[k][j] = mu[k1][j];
mu[k1][j] = t;
}
}
C = B[k] + m * m * B[k1];
mu[k][k1] = m * B[k1] / C;
for (i = 1; i <= n; i++)
{
c[i] = bs[k1][i];
}
for (i = 1; i <= n; i++)
{
bs[k1][i] = bs[k][i] + m * c[i];
}
for (i = 1; i <= n; i++)
{
bs[k][i] = -m * bs[k][i] + B[k] * c[i] / C;
}
B[k] *= B[k1] / C;
B[k1] = C;
for (i = k + 1; i <= kmax; i++)
{
t = mu[i][k];
mu[i][k] = mu[i][k1] - m * t;
mu[i][k1] = t + mu[k][k1] * mu[i][k];
}
}
bool LLL_Lattice::LLL(
int n,
std::vector<std::vector<double>>& b,
std::vector<std::vector<double>>& h)
{
// Lattice reduction algorithm
double m;
std::vector<double> B(n + 1);
std::vector<double> bv(n + 1);
std::vector<double> bw(n + 1);
std::vector<std::vector<double>> bs(n + 1,
std::vector<double>(n + 1));
std::vector<std::vector<double>> mu(n + 1,
std::vector<double>(n + 1));
int i, j, k, k1, kmax = 1, l;
for (i = 1; i <= n; i++)
bv[i] = bs[1][i] = b[1][i];
B[1] = Scalar(n, bv, bv);
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
h[i][j] = 0.0;
}
h[i][i] = 1.0;
}
for (k = 2; k <= n; k++)
{
if (k <= kmax)
goto Label3;
kmax = k;
for (i = 1; i <= n; i++)
{
bs[k][i] = b[k][i];
}
for (j = 1; j <= k - 1; j++)
{
for (l = 1; l <= n; l++)
{
bv[l] = b[k][l];
bw[l] = bs[j][l];
}
mu[k][j] = Scalar(n, bv, bw) / B[j];
for (i = 1; i <= n; i++)
{
bs[k][i] -= mu[k][j] * bs[j][i];
}
}
for (i = 1; i <= n; i++)
{
bv[i] = bs[k][i];
}
B[k] = Scalar(n, bv, bv);
if (B[k] == 0.0)
return false;
Label3:
k1 = k - 1;
m = mu[k][k1];
RED(k, k1, n, b, h, mu);
if (B[k] < (0.75 - m * m) * B[k1])
{
SWAP(k, k1, kmax, n, m, B, b, bs, h, mu);
k = max(2, k1);
goto Label3;
}
for (l = k - 2; l >= 1; l--)
{
RED(k, l, n, b, h, mu);
}
}
return true;
}
Blog Entry (c) Tuesday, August 27, 2024, Graphing New Goldwasser-Kilian Primality Test Results by James Pate Williams, Jr.
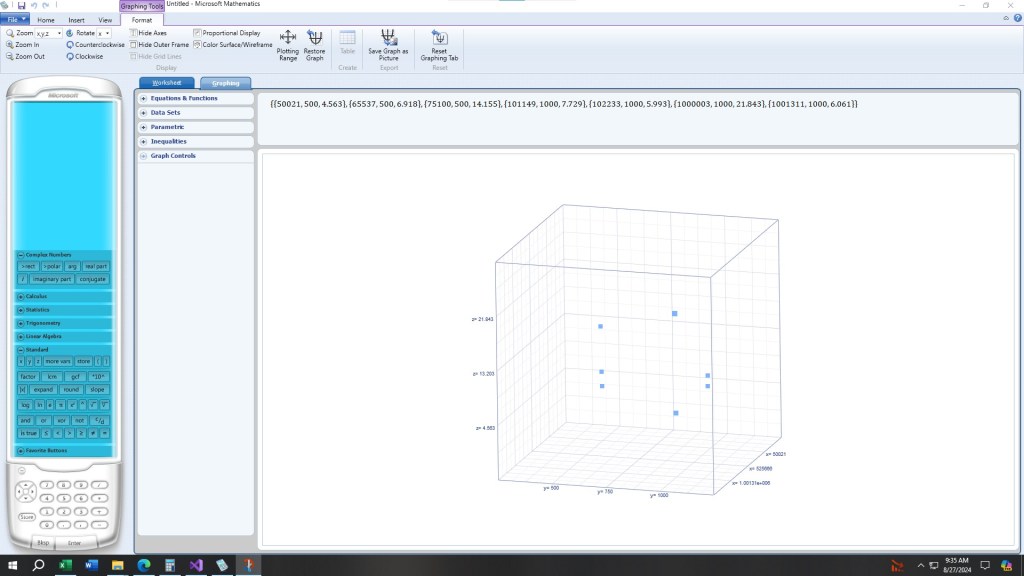
The x -axis is the number to be tested, the y-axis is prime number bound for factoring, and the z-axis is the runtime in seconds.
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. New and Improved Version of the Goldwasser-Kilian Primality Test
I corrected my powering modulo a prime routine. I added Pollard’s p – 1 factoring method and Shanks-Mestre elliptic curve point counting algorithm.
number to be tested or 0 to quit:
10000019
number of primes in factor base:
10000
Prime sieving time = 3.220000
N[0] = 10000019
a = 7838973
b = 2449531
m = 9995356
q = 356977
P = (9786147, 3226544)
P1 = (0, 1)
P2 = (5887862, 8051455)
N[1] = 356977
a = 45561
b = 178451
m = 357946
q = 178973
P = (80627, 163299)
P1 = (0, 1)
P2 = (52101, 282559)
N[2] = 178973
a = 135281
b = 76426
m = 178996
q = 73
P = (10238, 98035)
P1 = (0, 1)
P2 = (46702, 94326)
number is proven prime
runtime in seconds = 35.471000
number to be tested or 0 to quit:
10015969
number of primes in factor base:
10000
Prime sieving time = 3.424000
N[0] = 10015969
a = 6613193
b = 3951715
m = 10013908
q = 2503477
P = (998314, 8329764)
P1 = (0, 1)
P2 = (6944357, 1053776)
N[1] = 2503477
a = 1175442
b = 379813
m = 2505736
q = 293
P = (646462, 1631861)
P1 = (0, 1)
P2 = (1477980, 88719)
number is proven prime
runtime in seconds = 5.612000
number to be tested or 0 to quit:
99997981
number of primes in factor base:
10000
Prime sieving time = 4.152000
N[0] = 99997981
a = 34129462
b = 80482974
m = 100001414
q = 181
P = (19305995, 40493835)
P1 = (0, 1)
P2 = (33828245, 72969559)
number is proven prime
runtime in seconds = 11.500000
number to be tested or 0 to quit:
100001819
number of primes in factor base:
100000
Prime sieving time = 3.218000
N[0] = 100001819
a = 2694060
b = 17329746
m = 100008102
q = 5569
P = (124594, 14596756)
P1 = (0, 1)
P2 = (32514144, 56926555)
number is proven prime
runtime in seconds = 76.301000
number to be tested or 0 to quit:
100005317
number of primes in factor base:
100000
Prime sieving time = 3.269000
N[0] = 100005317
a = 45478318
b = 328034
m = 99988256
q = 3124633
P = (62548529, 30179124)
P1 = (0, 1)
P2 = (70379514, 76899689)
N[1] = 3124633
a = 2605576
b = 1809212
m = 3127654
q = 503
P = (1236288, 2081401)
P1 = (0, 1)
P2 = (2264479, 2583693)
number is proven prime
runtime in seconds = 459.979000
number to be tested or 0 to quit:
100000007
number of primes in factor base:
100000
Prime sieving time = 3.209000
N[0] = 100000007
a = 50593669
b = 72502607
m = 100005736
q = 2053
P = (72365335, 69885097)
P1 = (0, 1)
P2 = (55023241, 20078454)
number is proven prime
runtime in seconds = 163.705000
number to be tested or 0 to quit:
100014437
number of primes in factor base:
100000
Prime sieving time = 3.919000
N[0] = 100014437
a = 49955472
b = 45482796
m = 100024160
q = 263
P = (41650735, 8652103)
P1 = (0, 1)
P2 = (53790105, 37282431)
number is proven prime
runtime in seconds = 12.915000
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. Single Precision (64-Bit) Version of Pollard’s P-1 Factoring Method
prime number sieve creation
time in seconds = 3.483000
number to be factored or 0 to quit:
2111222333
1 11 1 p
2 17 1 p
3 11289959 1 p
factoring time in seconds = 0.063000
number to be factored or 0 to quit:
1234567890
1 2 1 p
2 3 2 p
3 5 1 p
4 3607 1 p
5 3803 1 p
factoring time in seconds = 0.133000
number to be factored or 0 to quit:
2^30+0
prime powers are not allowed
number to be factored or 0 to quit:
0
Blog Entry (c) Tuesday, August 20, 2024, by James Pate Williams, Jr. More Goldwasser-Kilian Primality Results (64-Bit Version which I call Single Precision)
Blog Entry (c) Monday, August 19, 2024, by James Pate Williams, Jr. Results from a Corrected Version of my Implementation of the 64-Bit Goldwasser-Kilian Primality Test
Blog Entry (c) Saturday, August 10, 2024, by James Pate Williams, Jr. The LLL Lattice Reduction Algorithm
Factorizations of Some Fibonacci Sequence Numbers, Lucas Sequence Numbers and Some Other Numbers Using Arjen K. Lenstra’s Free Large Integer Package and the Elliptic Curve Method (c) January 28, 2024, by James Pate Williams, Jr.
All of the following computations were performed on a late 2015 Dell XPS 8900 personal computer with a 64-bit Intel Core I7 processor @ 4.0GHz with 16GB of DDR2 RAM.
Factorization of Six Fibonacci Sequence Numbers:
Fibonacci 500
# digits 105
5 ^ 2 p # digits 1
15 c # digits 2
101 p # digits 3
401 p # digits 3
1661 c # digits 4
3001 p # digits 4
10291 c # digits 5
570601 p # digits 6
112128001 p # digits 9
1353439001 p # digits 10
28143378001 p # digits 11
5465167948001 p # digits 13
84817574770589638001 p # digits 20
158414167964045700001 p # digits 21
Runtime (s) = 1.206000
Fibonacci 505
# digits 106
5 p # digits 1
743519377 p # digits 9
44614641121 p # digits 11
770857978613 p # digits 12
960700389041 p # digits 12
12588421794766514566269164716286291055826556238643852856601641 p # digits 62
Runtime (s) = 1.959000
Fibonacci 510
# digits 107
2 ^ 3 p # digits 1
11 p # digits 2
61 p # digits 2
1021 p # digits 4
1597 p # digits 4
3469 p # digits 4
3571 p # digits 4
9521 p # digits 4
53551 p # digits 5
95881 p # digits 5
142445 c # digits 6
1158551 p # digits 7
3415914041 p # digits 10
20778644396941 p # digits 14
20862774425341 p # digits 14
81358225616651 c # digits 14
162716451241291 p # digits 15
Runtime (s) = 2.682000
Fibonacci 515
# digits 108
5 p # digits 1
519121 p # digits 6
5644193 p # digits 7
512119709 p # digits 9
84388938382141 p # digits 14
300367026458796424297447559250634818495937628065437243817852436228914621 p # digits 72
Runtime (s) = 7.861000
Fibonacci 520
# digits 109
131 p # digits 3
451 c # digits 3
521 p # digits 3
2081 p # digits 4
2161 p # digits 4
3121 p # digits 4
24571 p # digits 5
90481 p # digits 5
2519895 c # digits 7
21183761 p # digits 8
57089761 p # digits 8
102193207 p # digits 9
1932300241 p # digits 10
14736206161 p # digits 11
5836312049326721 p # digits 16
42426476041450801 p # digits 17
Runtime (s) = 5.155000
Fibonacci 525
# digits 110
2 p # digits 1
5 p # digits 1
421 p # digits 3
701 p # digits 3
3001 p # digits 4
3965 c # digits 4
4201 p # digits 4
141961 p # digits 6
2553601 p # digits 7
230686501 p # digits 9
8288823481 p # digits 10
82061511001 p # digits 11
19072991752501 c # digits 14
8481116649425701 p # digits 16
17231203730201189308301 p # digits 23
Runtime (s) = 2.026000
Factorization of Six Lucas Sequence Numbers
Lucas 340
113709744839525149336680459091826532688903186653162057995534262332121127
# digits 72
7 p # digits 1
2161 p # digits 4
5441 p # digits 4
897601 p # digits 6
23230657239121 p # digits 14
17276792316211992881 p # digits 20
3834936832404134644974961 p # digits 25
Runtime (s) = 109.103000
Lucas 345
# digits 73
2 ^ 2 p # digits 1
31 p # digits 2
461 p # digits 3
1151 p # digits 4
1529 c # digits 4
324301 p # digits 6
686551 p # digits 6
1485571 p # digits 7
4641631 p # digits 7
19965899801 c # digits 11
117169733521 p # digits 12
3490125311294161 p # digits 16
Runtime (s) = 0.032000
Lucas 350
13985374084677485786380981408251904922622980674054858121032362563653278123
# digits 74
3 p # digits 1
401 p # digits 3
2801 p # digits 4
11521 c # digits 5
28001 p # digits 5
570601 p # digits 6
12317523121 p # digits 11
248773766357061401 p # digits 18
7358192362316341243805801 p # digits 25
Runtime (s) = 21.047000
Lucas 355
69362907070206748494476200566565775354902428015845969798000696945226974645
# digits 74
5 p # digits 1
4261 p # digits 4
6673 p # digits 4
75309701 p # digits 8
309273161 p # digits 9
46165371073 p # digits 11
9207609261398081 p # digits 16
49279722643391864192801 p # digits 23
Runtime (s) = 40.726000
Lucas 360
769246427201094785080787978422393713094534885688979999504447628313150135520
# digits 75
2 ^ 5 p # digits 1
3 ^ 2 p # digits 1
23 p # digits 2
41 p # digits 2
105 c # digits 3
107 p # digits 3
241 p # digits 3
2161 p # digits 4
2521 p # digits 4
3439 c # digits 4
8641 p # digits 4
20641 p # digits 5
103681 p # digits 6
109441 p # digits 6
191306797 c # digits 9
10783342081 p # digits 11
13373763765986881 p # digits 17
Runtime (s) = 0.032000
Lucas 365
19076060504701386559675231910437330047906343529583769121365013189782992678011
# digits 77
11 p # digits 2
151549 p # digits 6
514651 p # digits 6
7015301 p # digits 7
8942501 p # digits 7
9157663121 p # digits 10
11899937029 p # digits 11
3252336525249736694804553589211 p # digits 31
The following two numbers were first factorized by J. M. Pollard on an 8-bit Phillips P2012 personal computer with 64 KB RAM and two 640 KB disc drives. The times required by Pollard were 41 and 47 hours.
2^144-3
22300745198530623141535718272648361505980413
# digits 44
492729991333 p # digits 12
45259565260477899162010980272761 p # digits 32
Runtime (s) = 0.086000
2^153+3
11417981541647679048466287755595961091061972995
# digits 47
5 p # digits 1
11 p # digits 2
600696432006490087537 p # digits 21
345598297796034189382757 p # digits 24
Runtime (s) = 0.676000
Partial factorization of the Twelfth Fermat Number 2^4096+1
# digits 1234
114689 p # digits 6
26017793 p # digits 8
63766529 p # digits 8
190274191361 p # digits 12
Runtime (s) = 1532.878000
Multiple Precision Arithmetic in C++ Implemented by James Pate Williams, Jr.
I have developed a long integer package in C++ using H. T. Lau’s “A Numerical Library in C for Scientists and Engineers”. That library is based on the NUMAL Numerical Algorithms in Algol library. I use 32-bit integers (long) as the basis of the LongInteger type. The base (radix) is 10000 which is the largest base using 32-bit integers. As a test of the library, I use Pollard’s original rho factorization method. I utilized the Alfred J. Menezes et al “Handbook of Applied Cryptography” Miller-Rabin algorithm and ANSI X9.17 pseudo random number generator with Triple-DES as the encryption algorithm. I translated Hans Riesel Pascal code for Euclid’s algorithm and the power modulus technique. I don’t use dynamic long integers a la Hans Riesel’s Pascal multiple precision library. The single precision is 32 32-bit longs and multiple precision 64 32-bit longs.
Here is a typical factorization:
Number to be factored, N = 3 1234 5678 9012
Factor = 3
Is Factor prime? 1
Factor = 4
Is Factor prime? 0
Factor = 102 8806 5751
Is Factor prime? 1
Function Evaluations = 6
Number to be factored, N = 0
The first number of N is the number of base 10000 digits. I verified that 10288065751 was prime using Miller-Rabin and the table found online below:
http://compoasso.free.fr/primelistweb/page/prime/liste_online_en.php
Numerical Explorations 