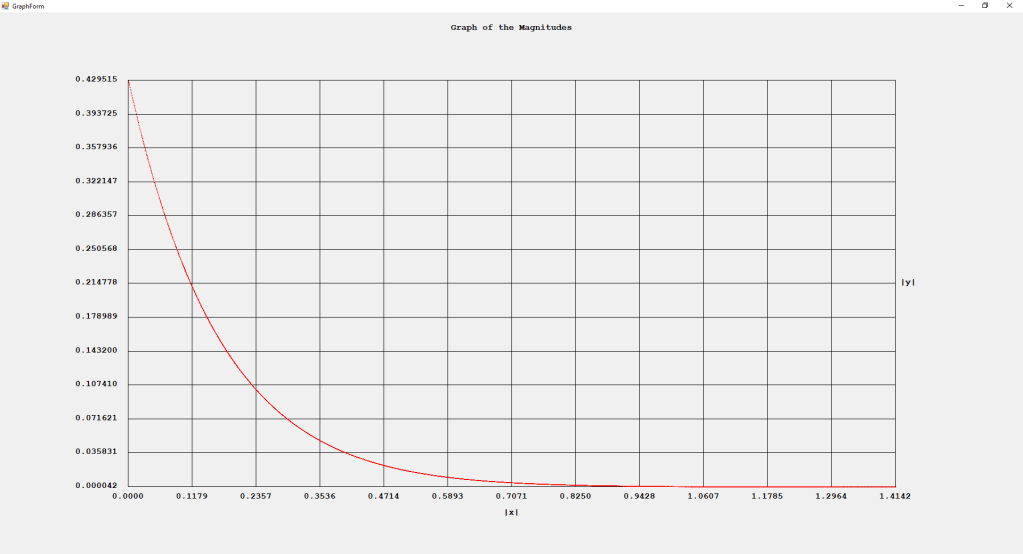
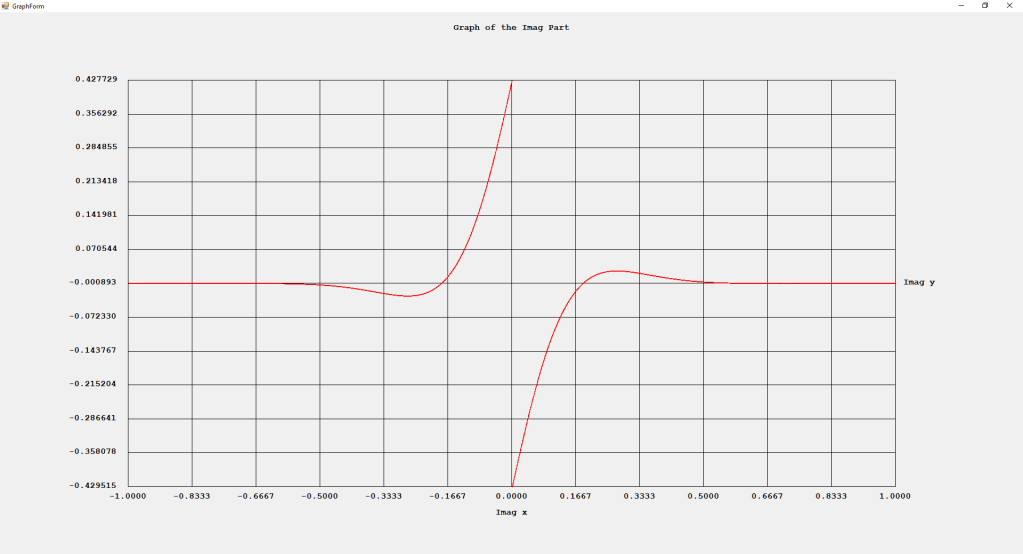
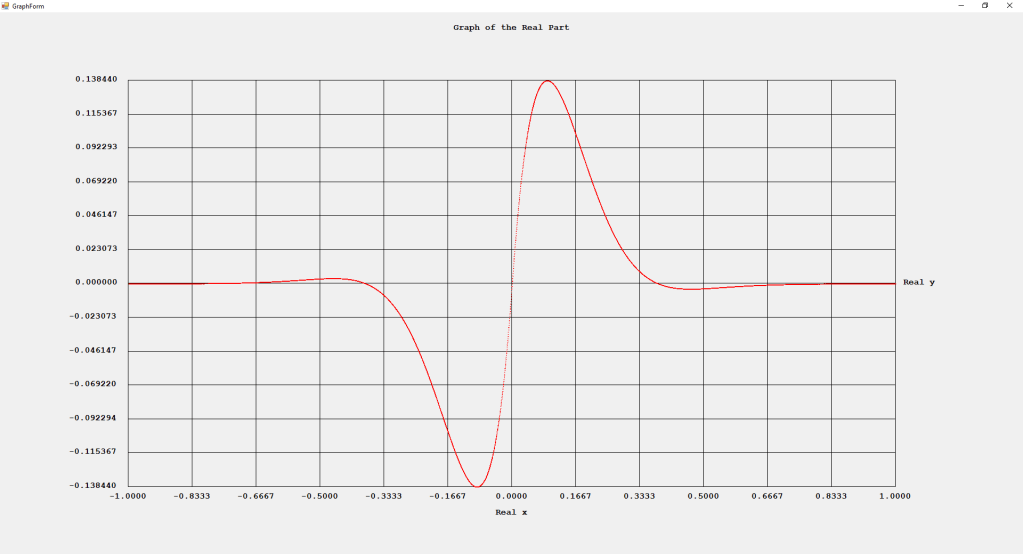
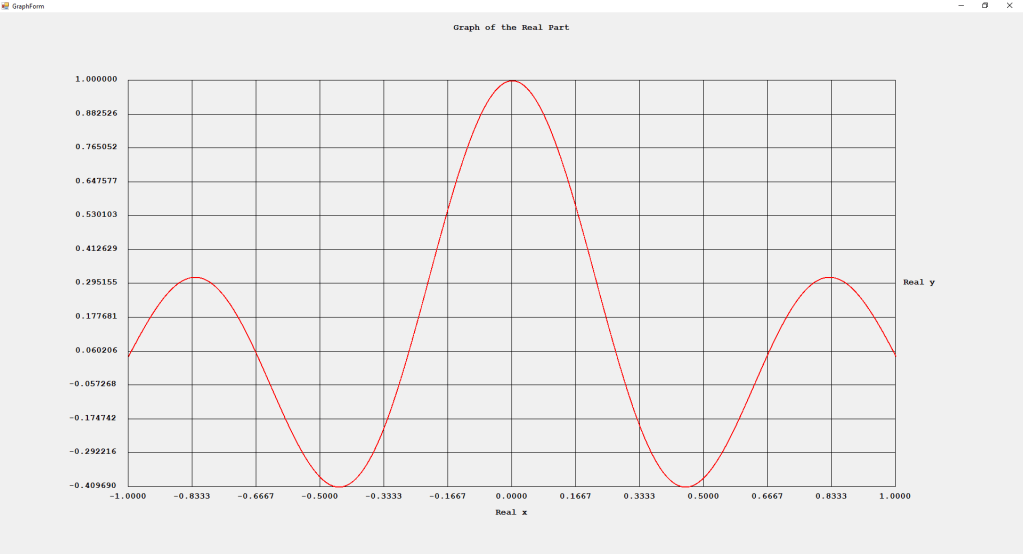
Category: Legendre Functions
New Jacobi Polynomials Application January 8, 2024, by James Pate Williams, Jr.
The two primary references used to create my application were: “A Numerical Library in C for Scientists and Engineers” by H. T. Lau and the following website: https://en.wikipedia.org/wiki/Jacobi_polynomials.
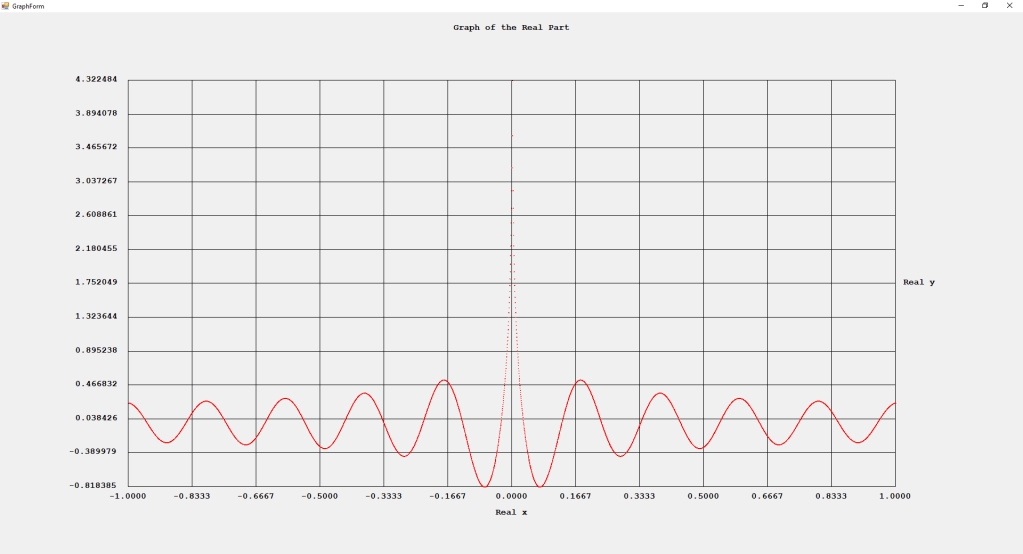
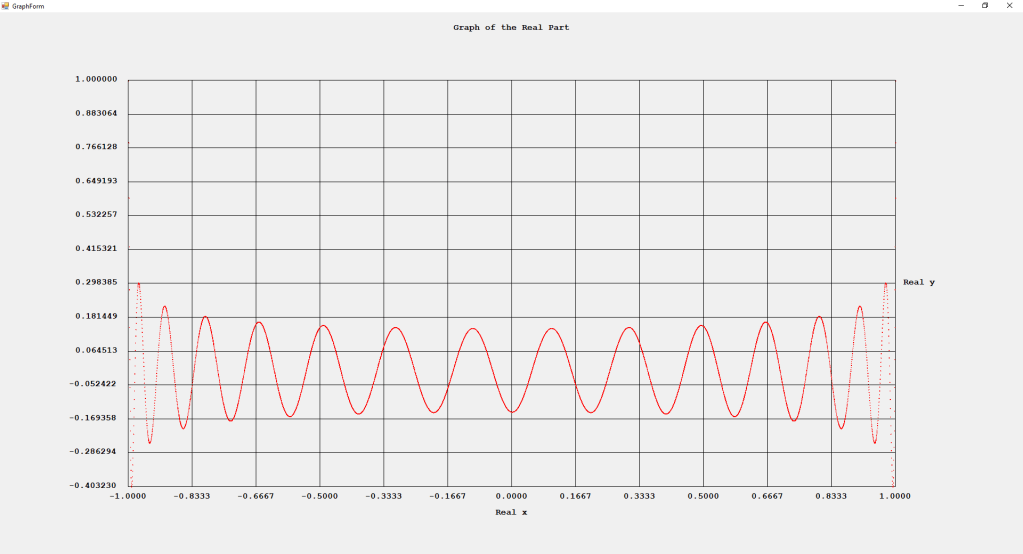
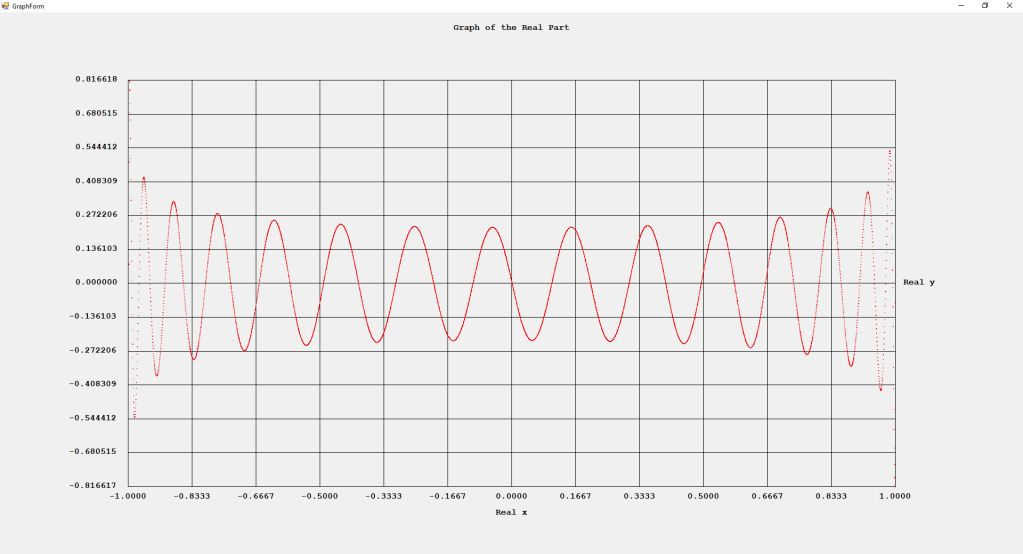
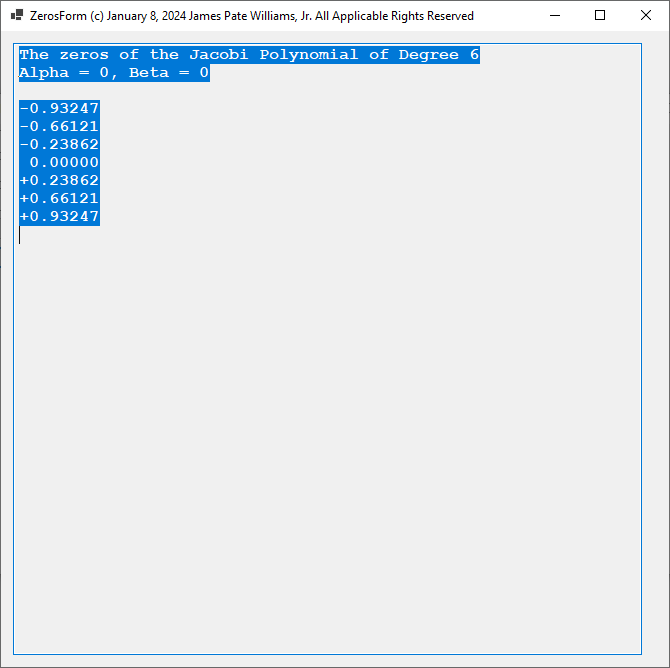
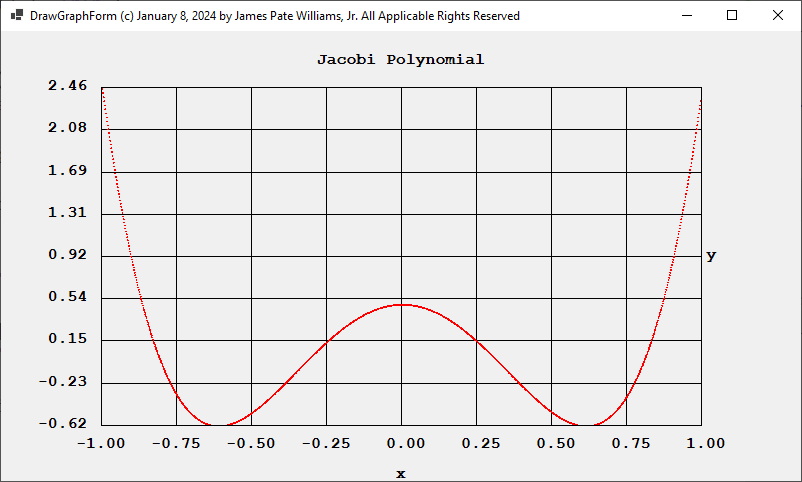
Using the Jacobi parameters alpha = 0 and beta = 0, we have the Legendre polynomials for degrees 4 and 6 and their associated roots:


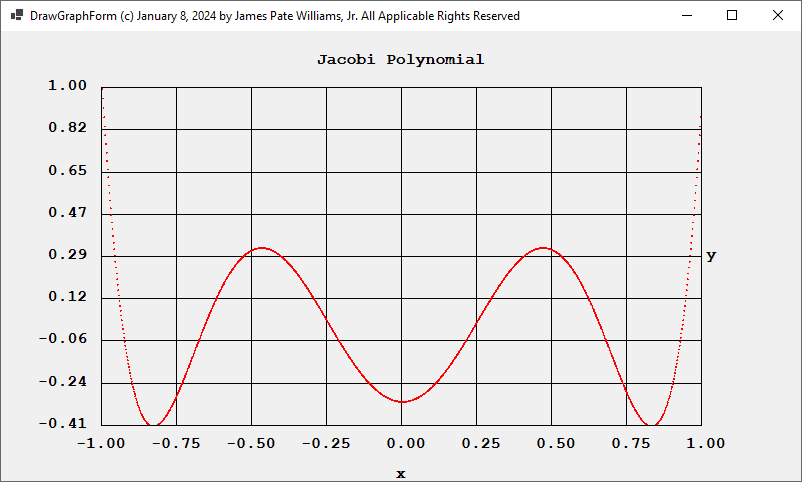
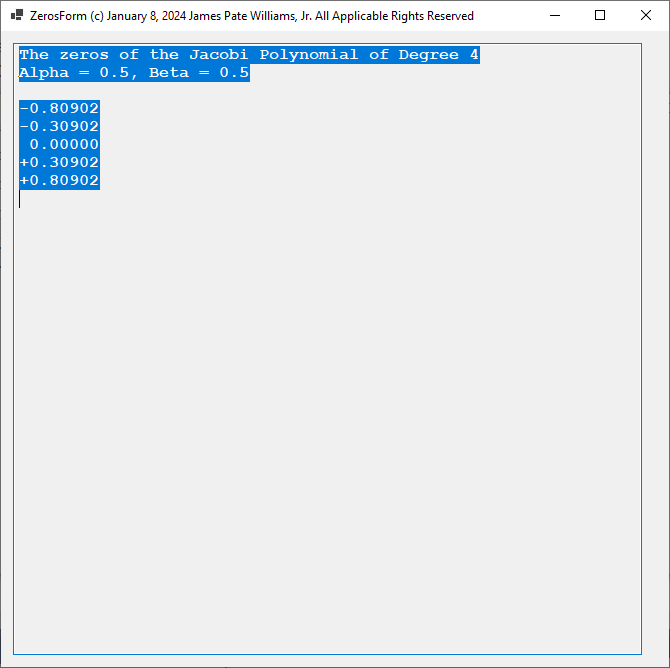
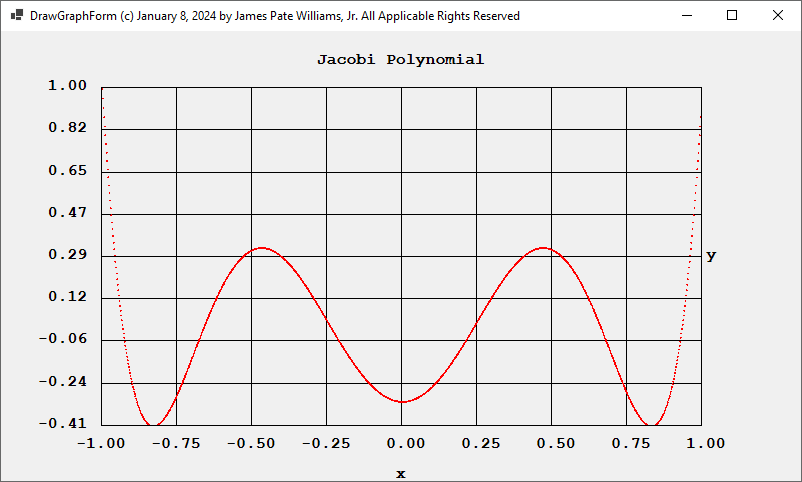
Using alpha = 0.5 and beta= 0.5 we obtain for degrees 4 and 6:

Electron Probability Distribution Function Etc. (c) James Pate Williams, Jr. December 2023
Partial Solution to a Neat Problem from an Online Textbook
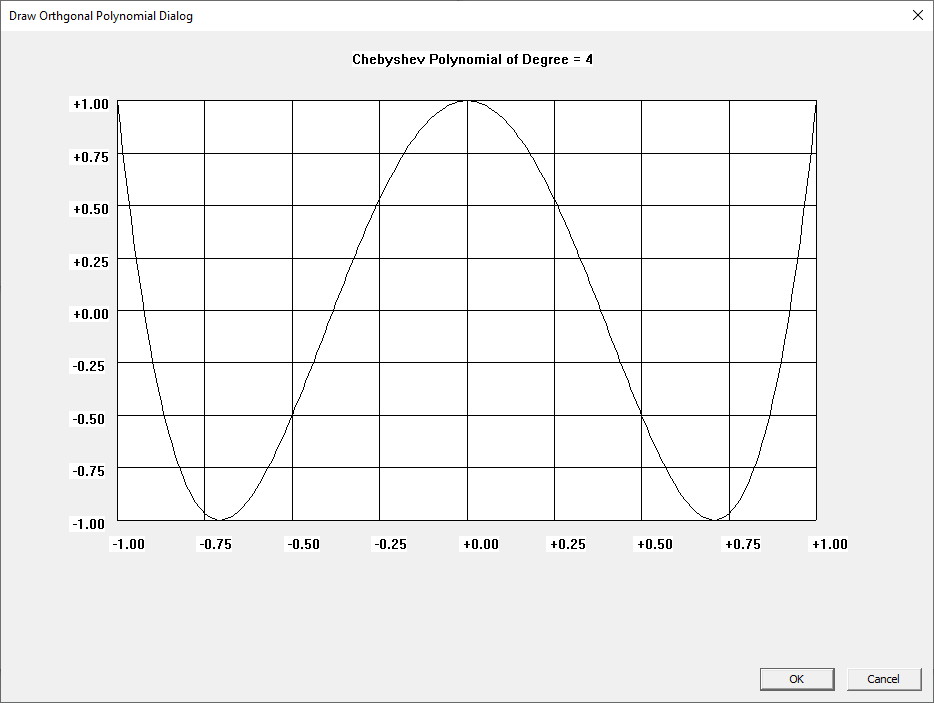
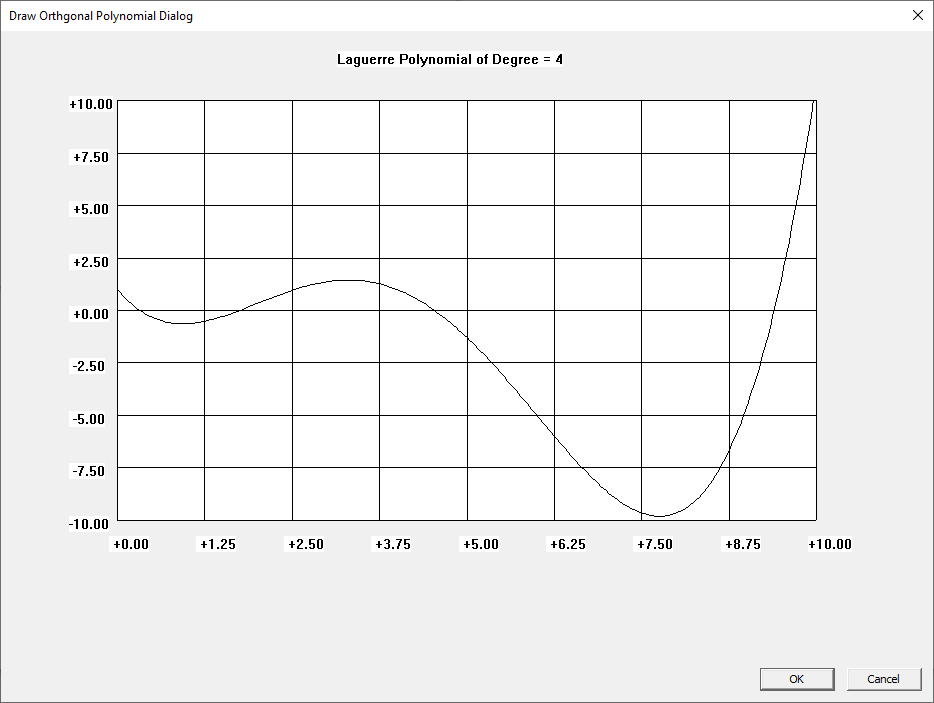
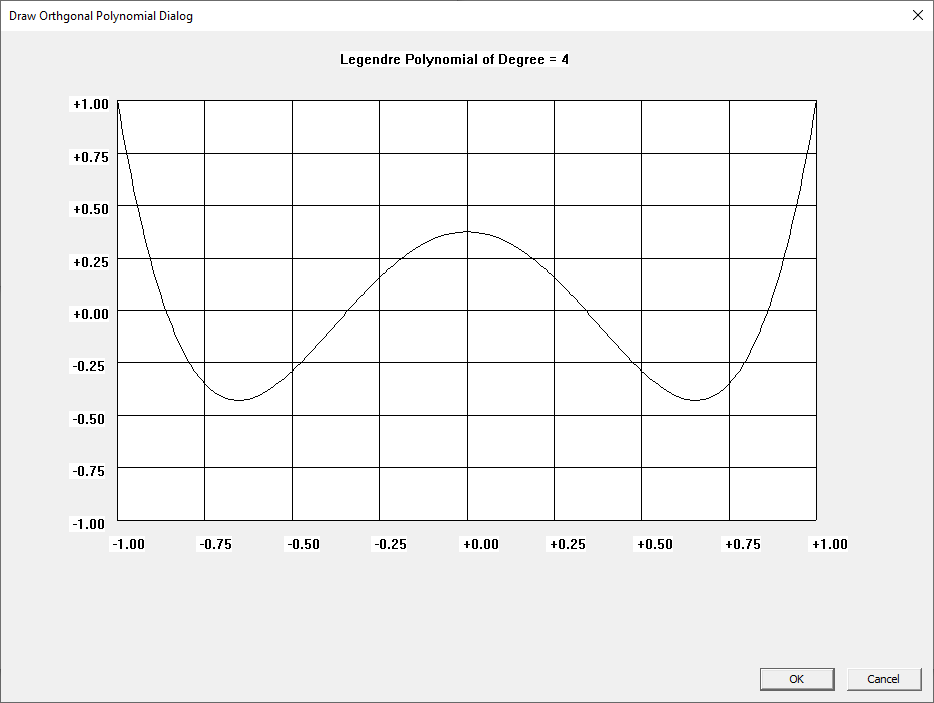
Win32 C Orthogonal Polynomials
I learned about the Laguerre and Legendre polynomials when I first read “Introduction to Quantum Mechanics” by Pauling and Wilson way back in the early 1970s. I later learned about the Chebyshev and other orthogonal polynomials. Beginning on March 30, 2015, I created yet another application to graph various orthogonal polynomials in C#. A few days ago, I wrote a Win32 C application to graph the Chebyshev, Laguerre, and Legendre orthogonal polynomials. At a later date, I will probably add Hermite and Jacobi polynomials.
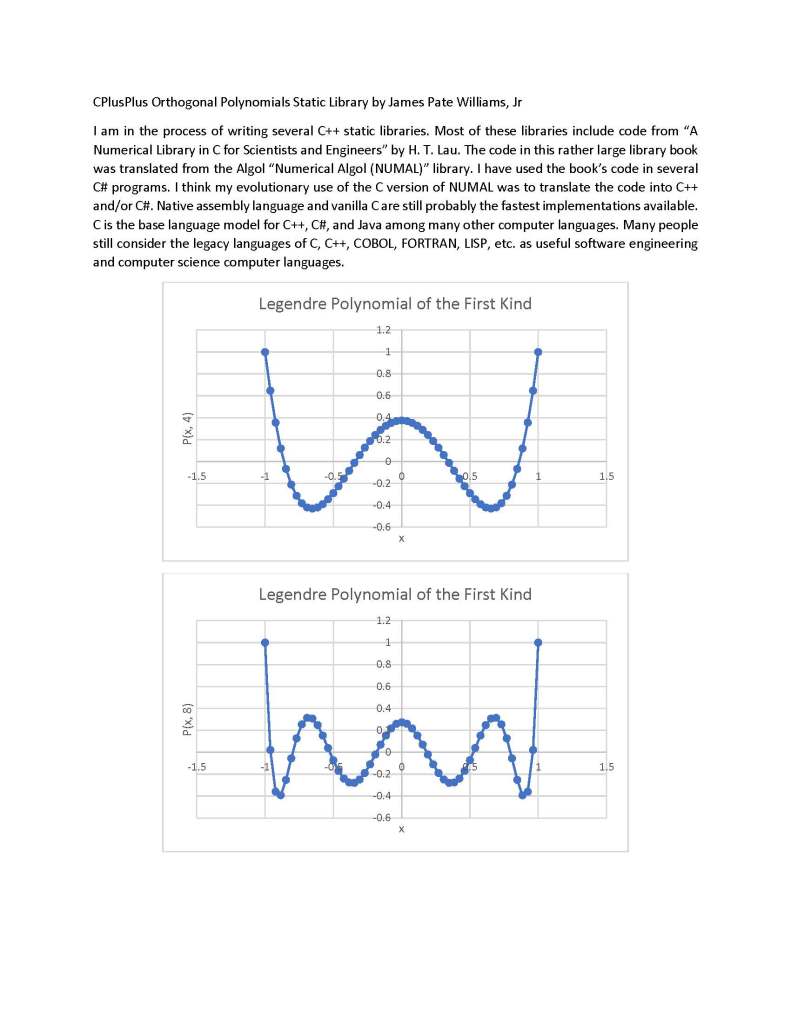
C++ Orthogonal Polynomials Static Library by James Pate Williams, Jr
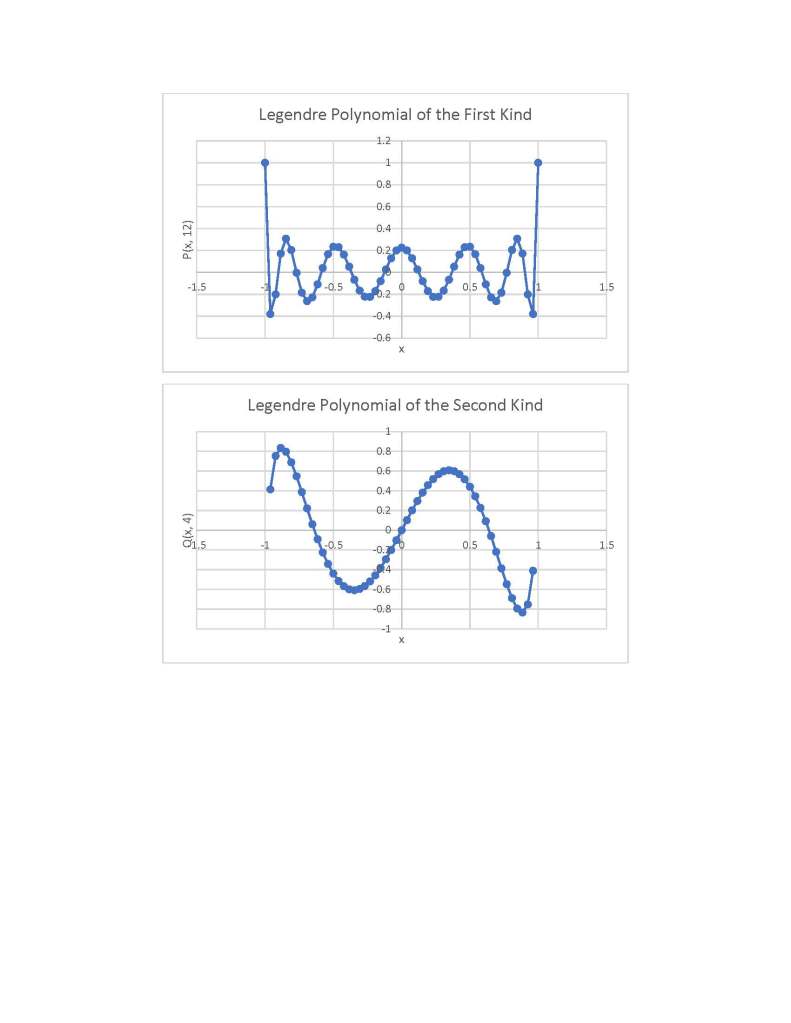
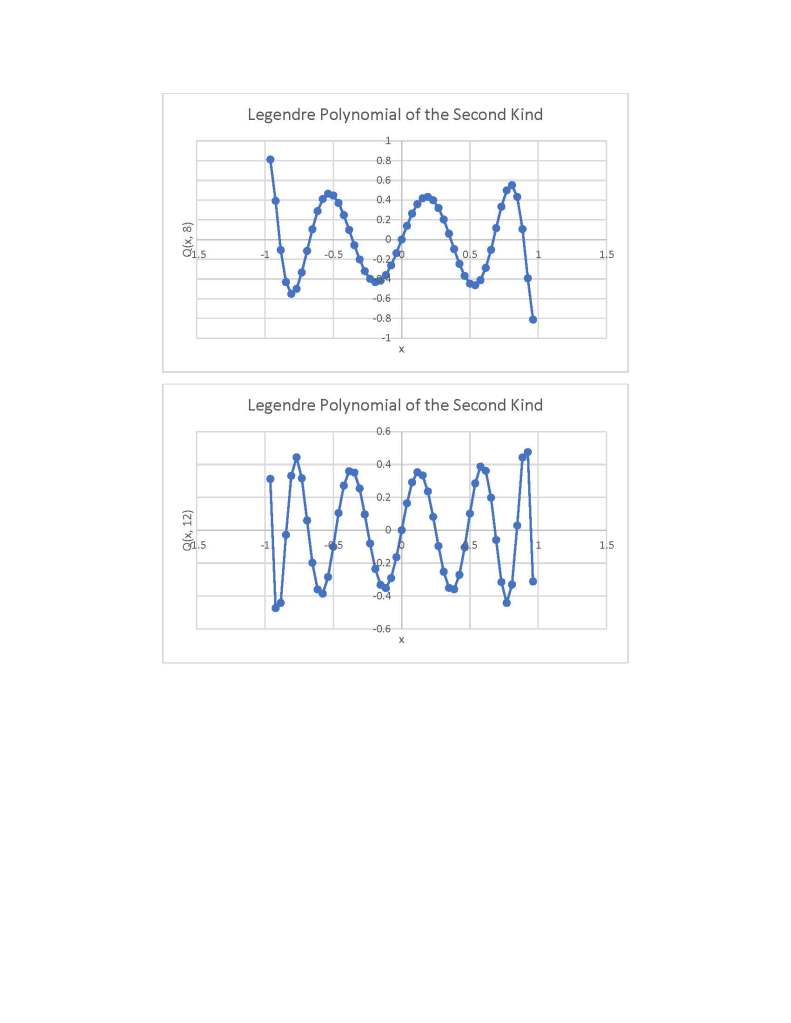
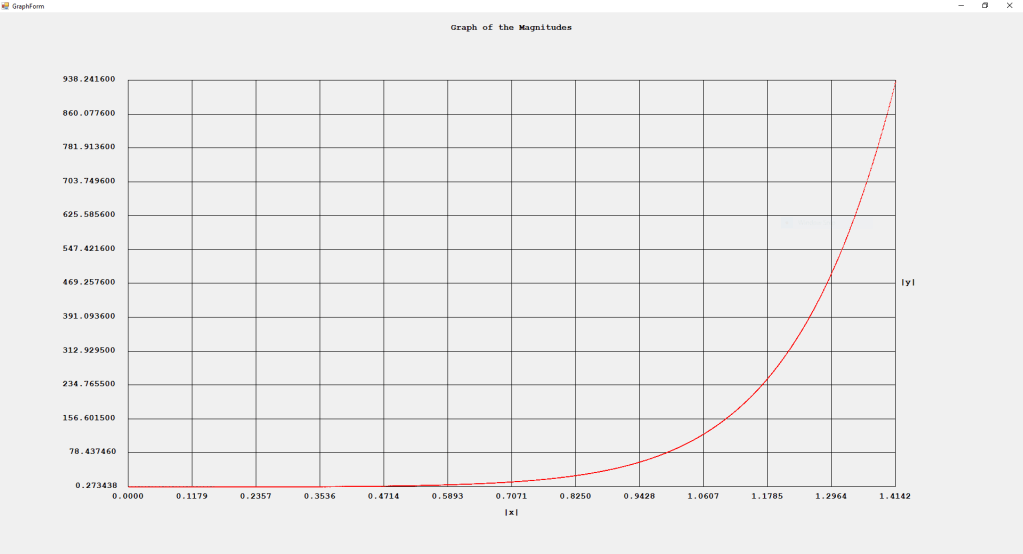
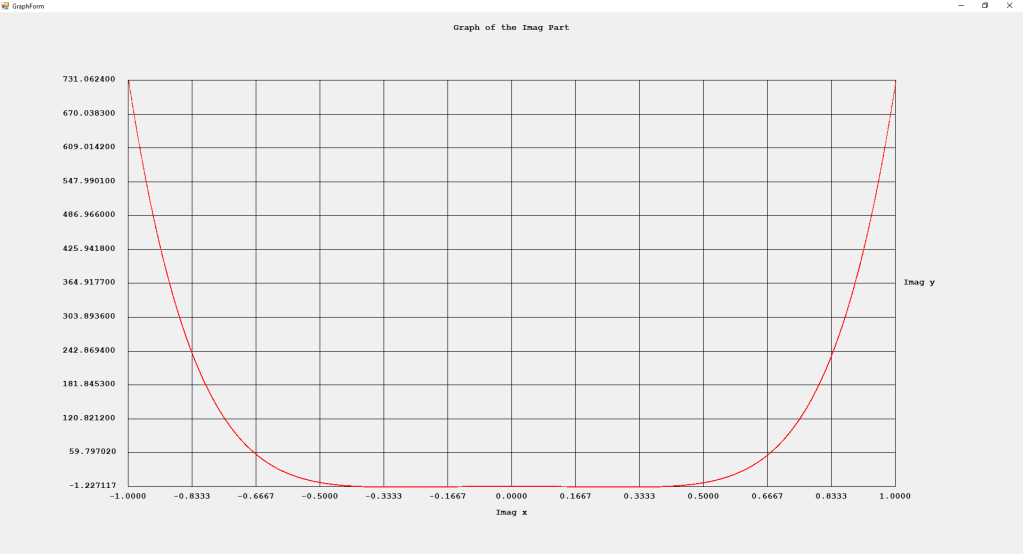
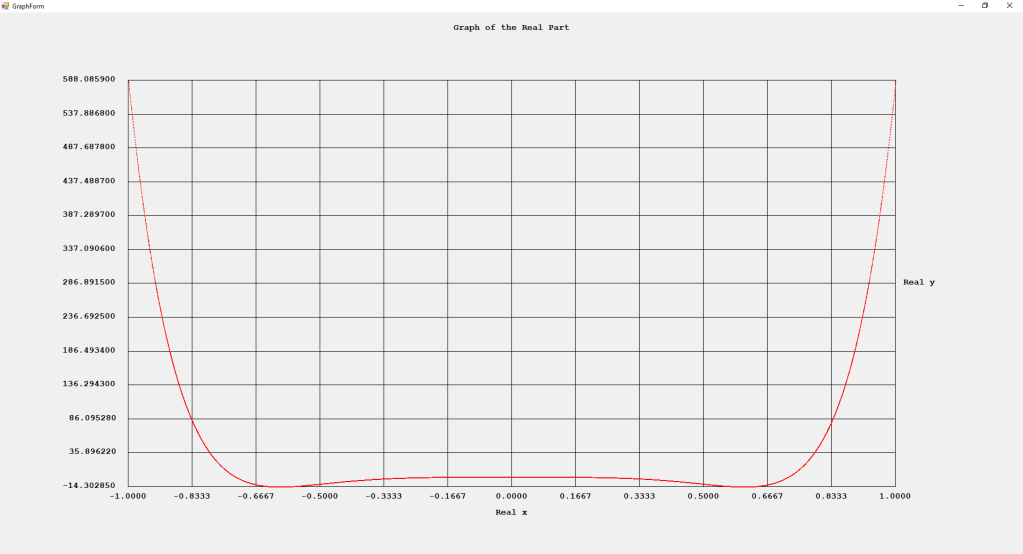
Three Term Recurrence Relations for the Legendre Functions by James Pate Williams, Jr.
bachelorthesis.dvi (uni-ulm.de)
My implementations and additional graphs for the Legendre functions mentioned in the thesis cited in the preceding line and PDF. The Legendre polynomials, functions, and associated functions have many applications in quantum mechanics and other branches of applied and theoretical physics.