Category: Numerical Analysis
Blog Entry of January 27, 2022 by James Pate Williams, Jr
Python Code to Implement the Linear Algebraic Rule by Cramer for a 3 by 3 Set of Linear Equations by James Pate Williams Jr
C++ Orthogonal Polynomials Static Library by James Pate Williams, Jr
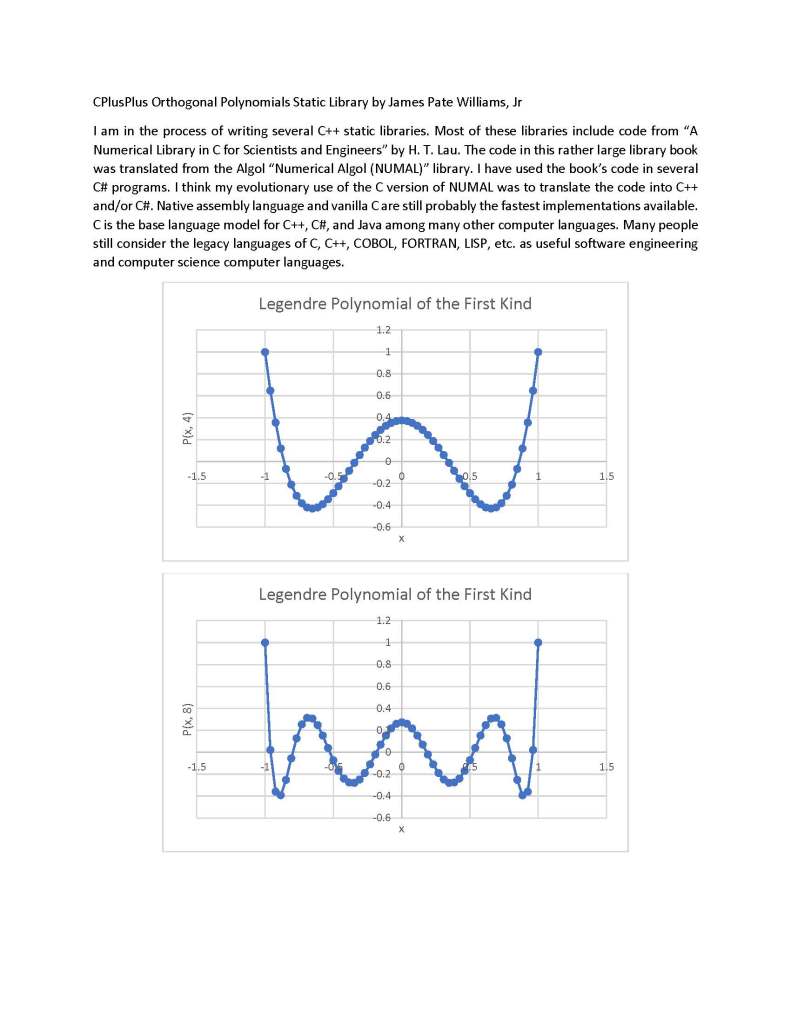
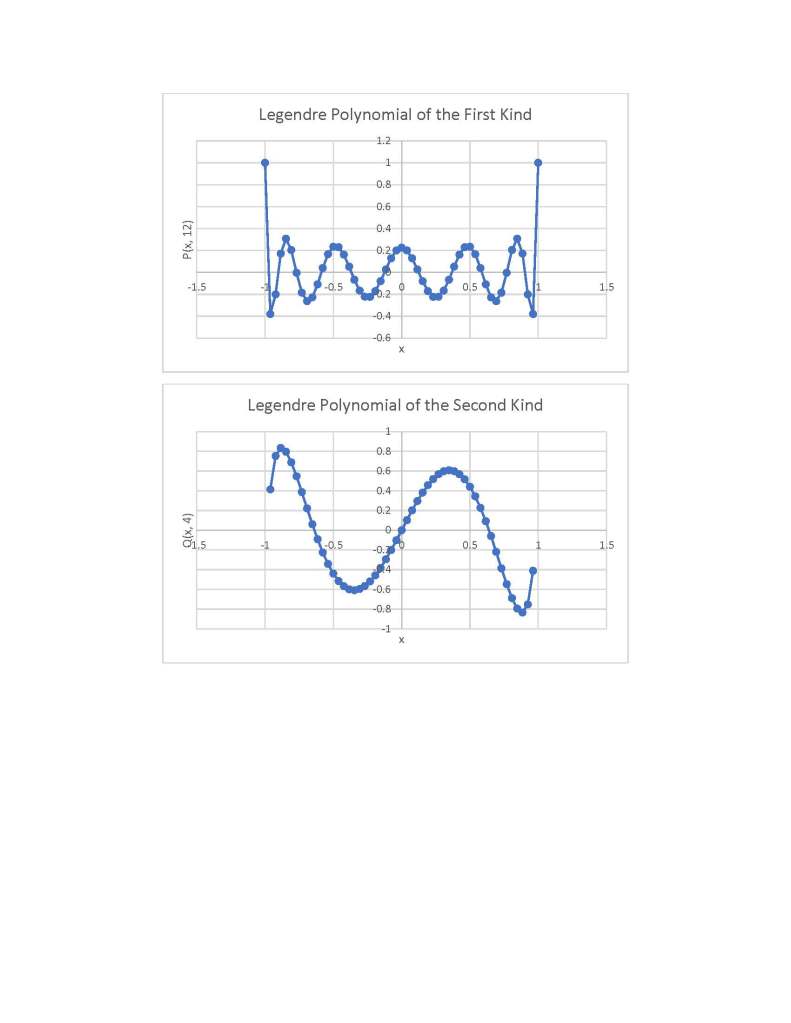
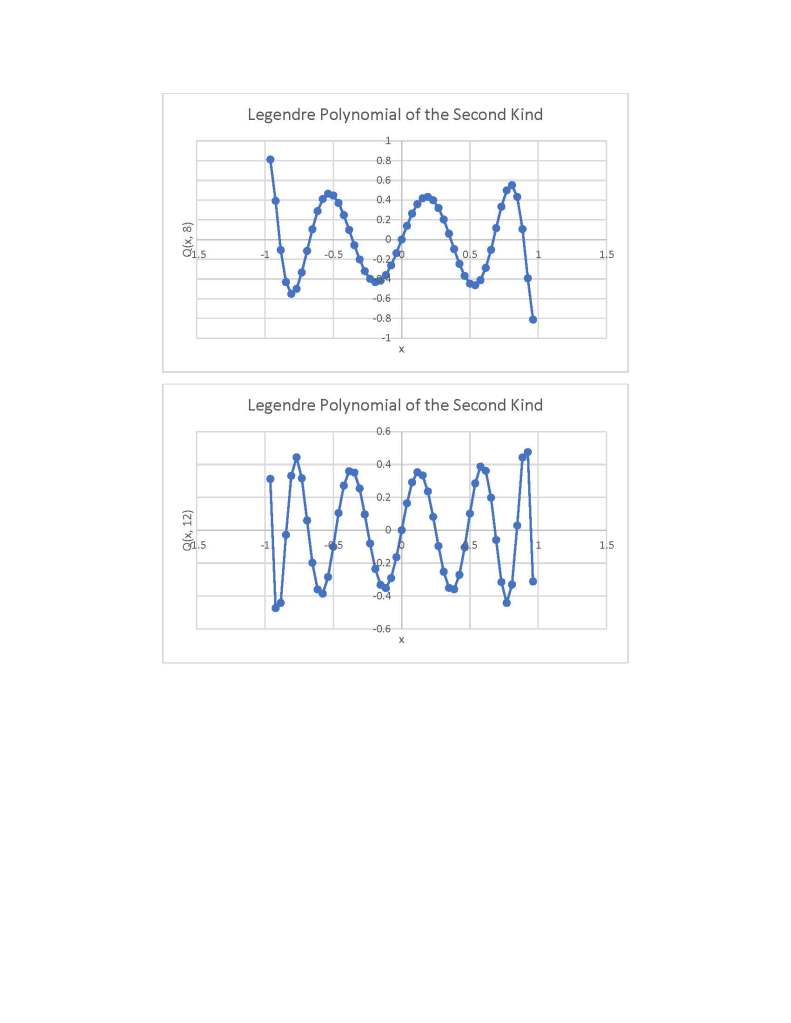
Three Term Recurrence Relations for the Legendre Functions by James Pate Williams, Jr.
bachelorthesis.dvi (uni-ulm.de)
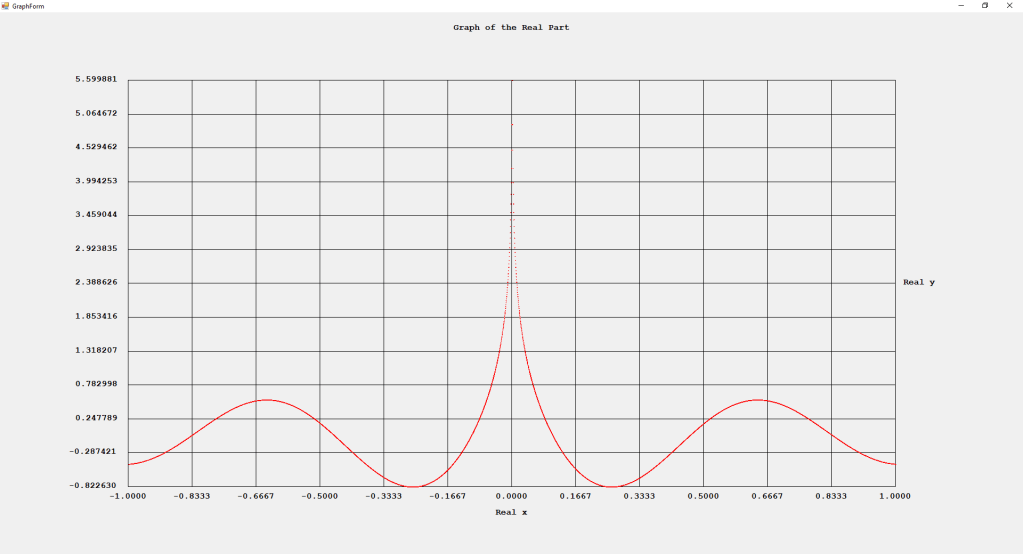
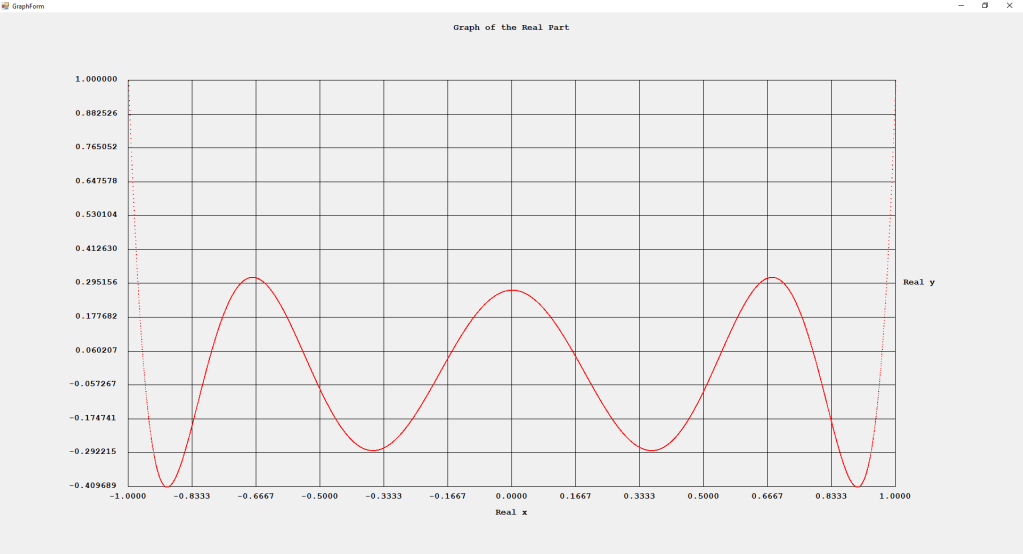
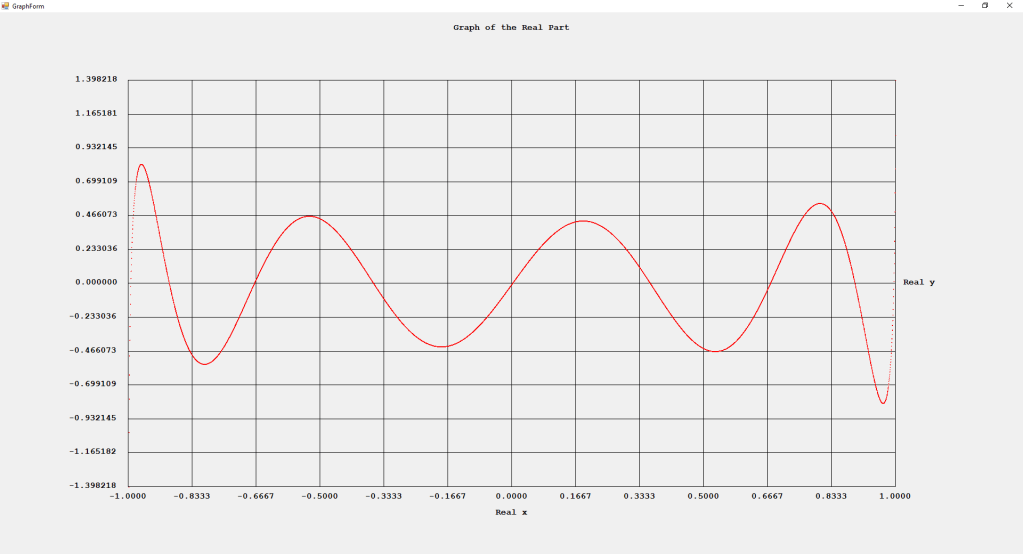
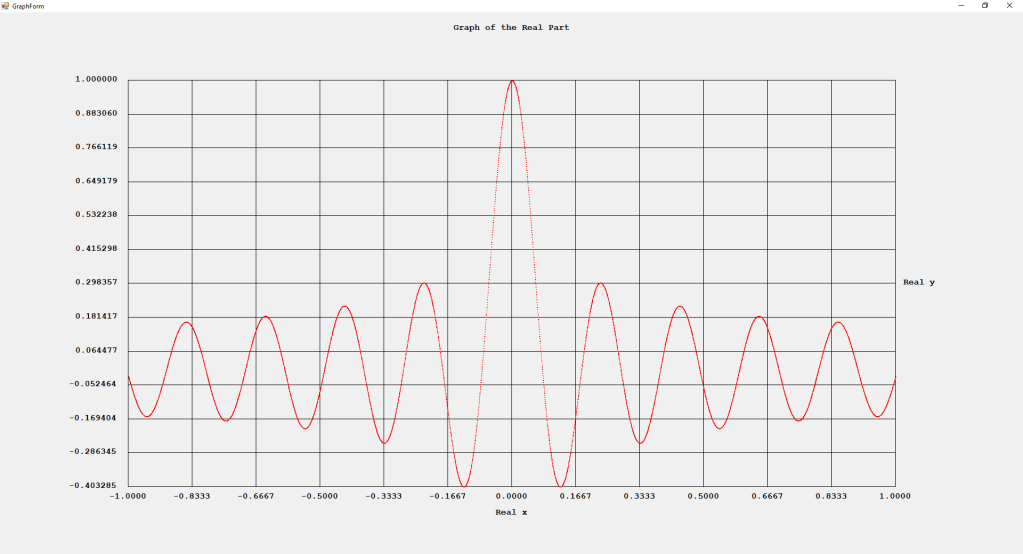
My implementations and additional graphs for the Legendre functions mentioned in the thesis cited in the preceding line and PDF. The Legendre polynomials, functions, and associated functions have many applications in quantum mechanics and other branches of applied and theoretical physics.
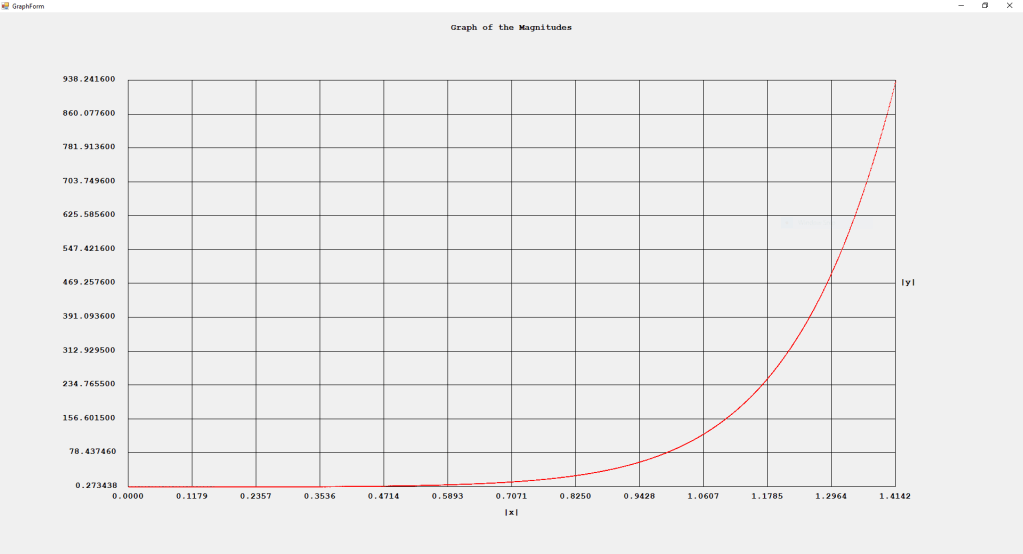
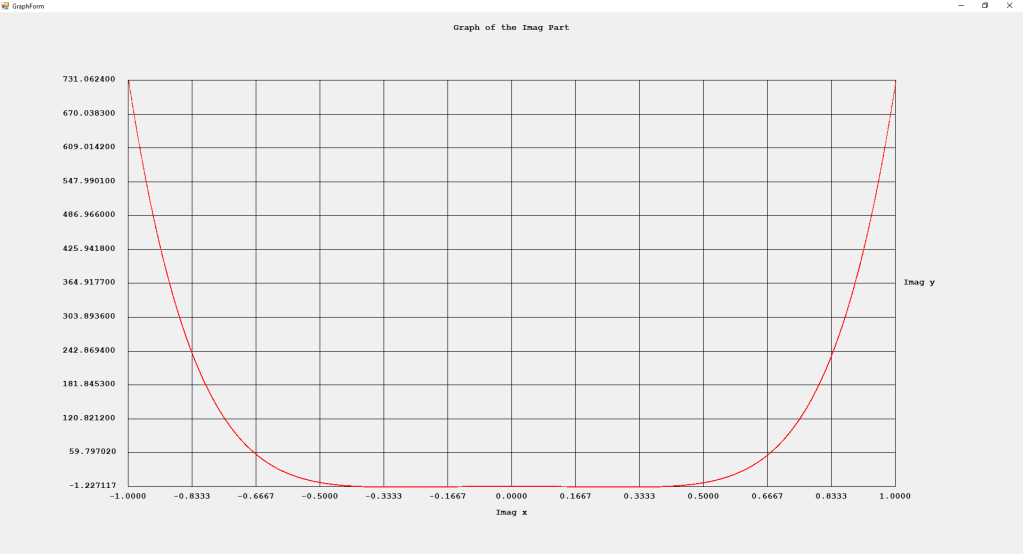
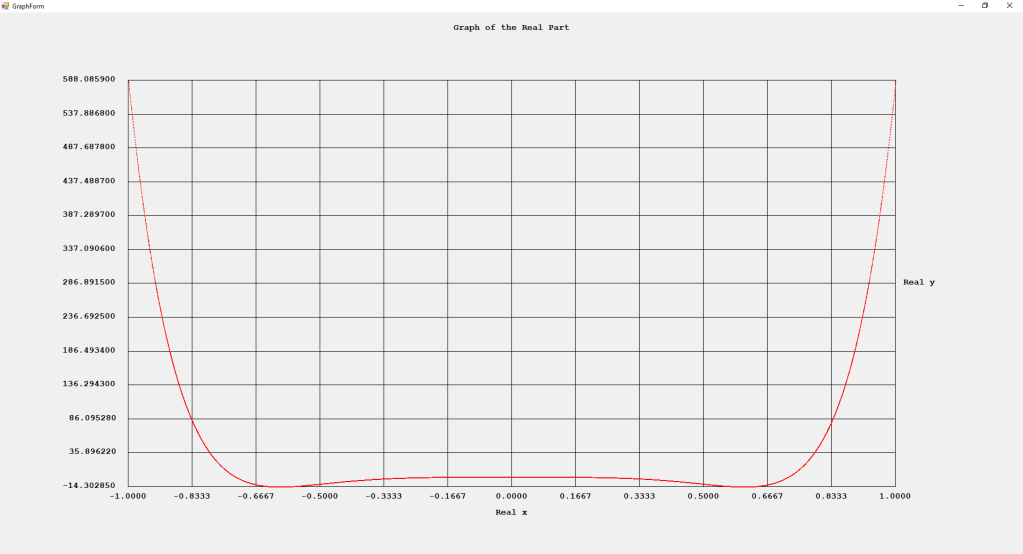
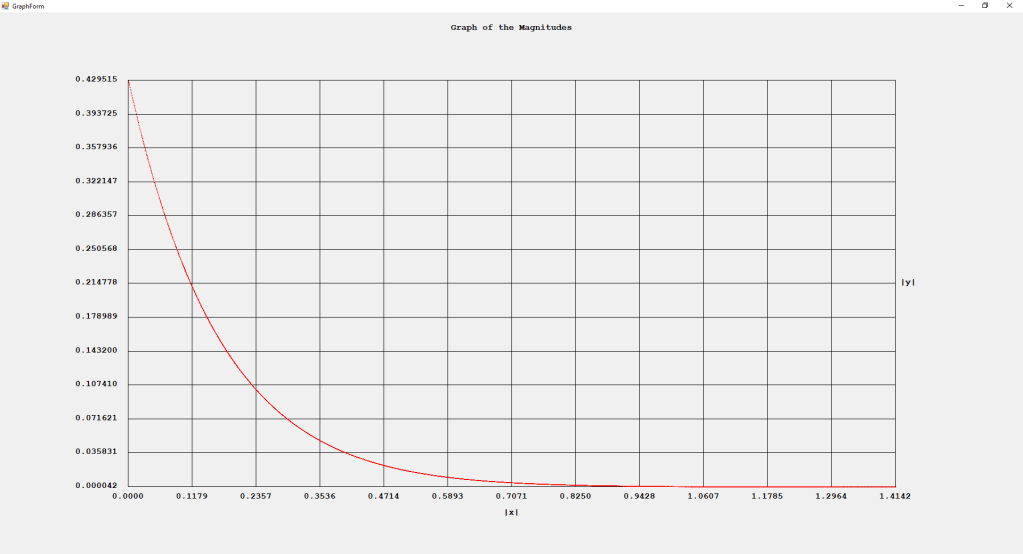
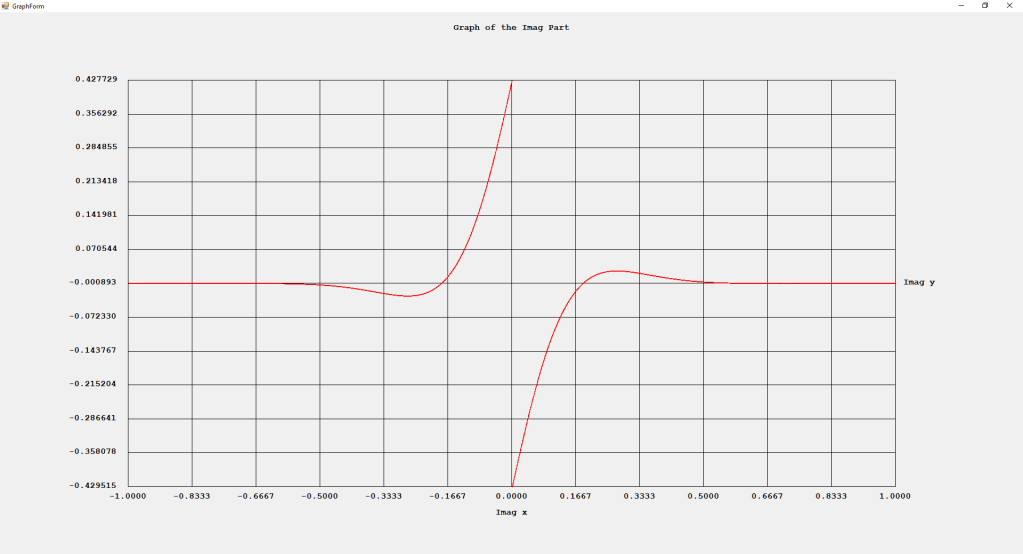
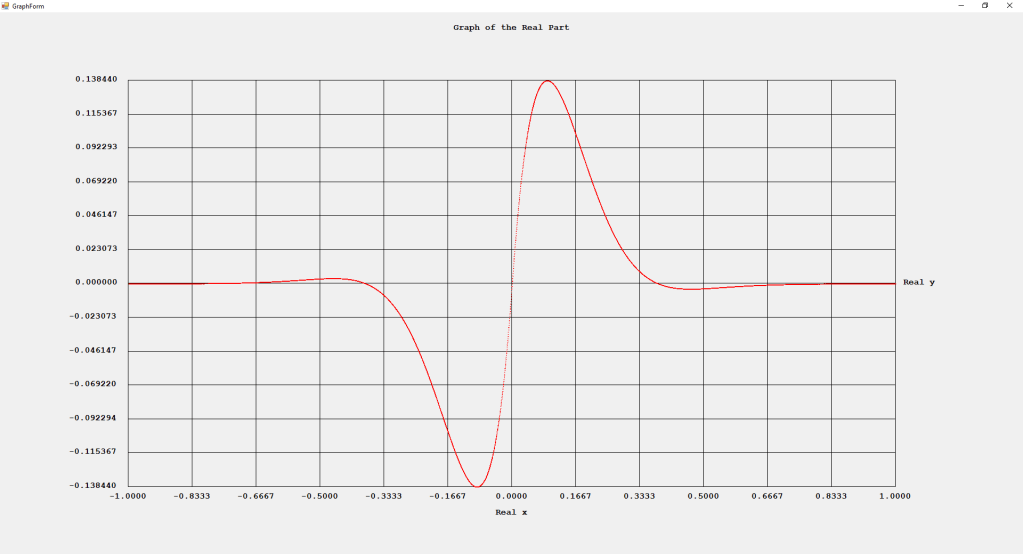
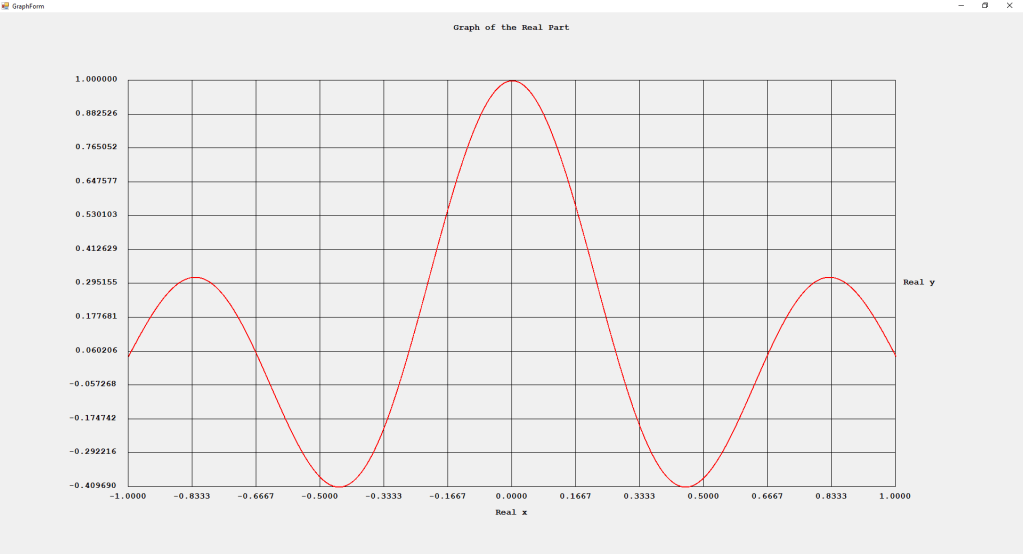
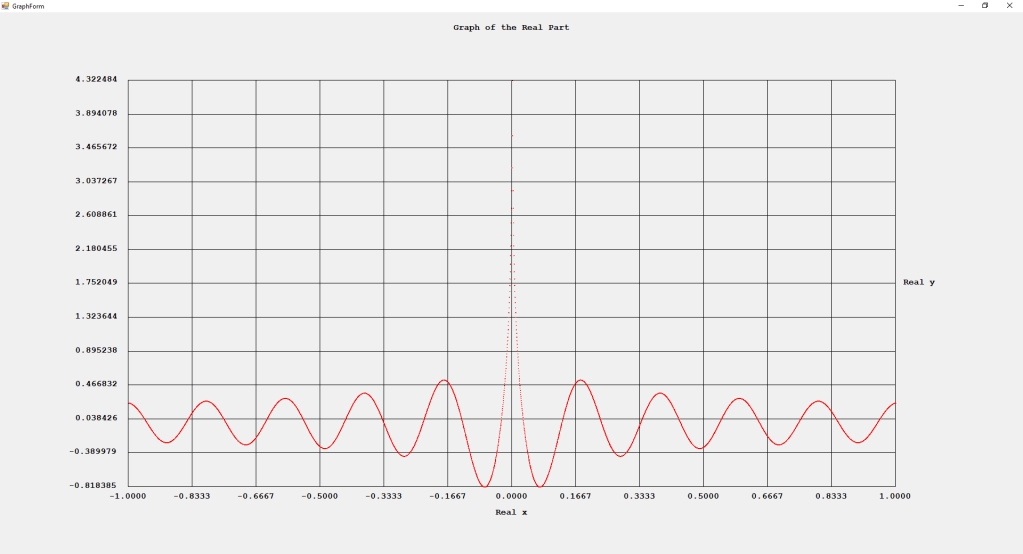
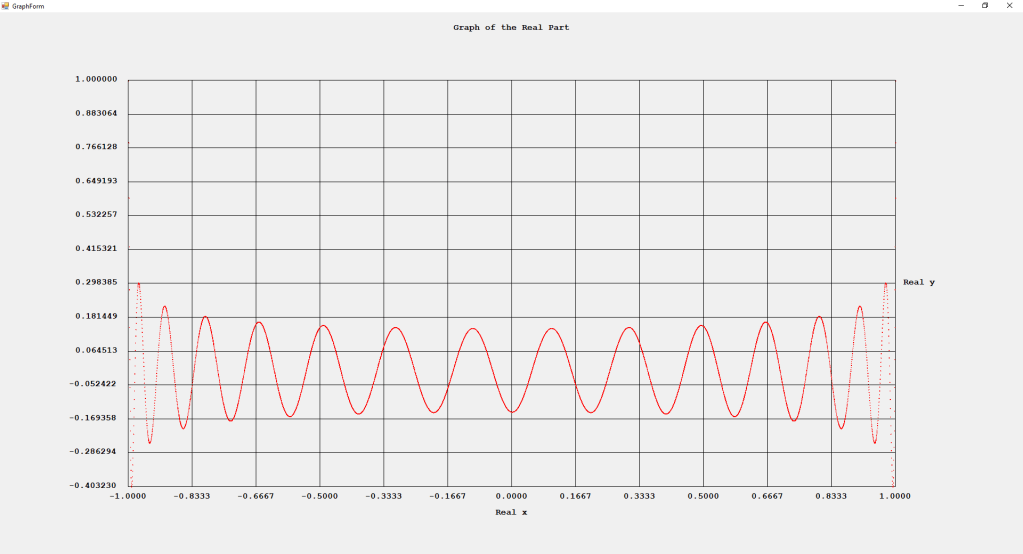
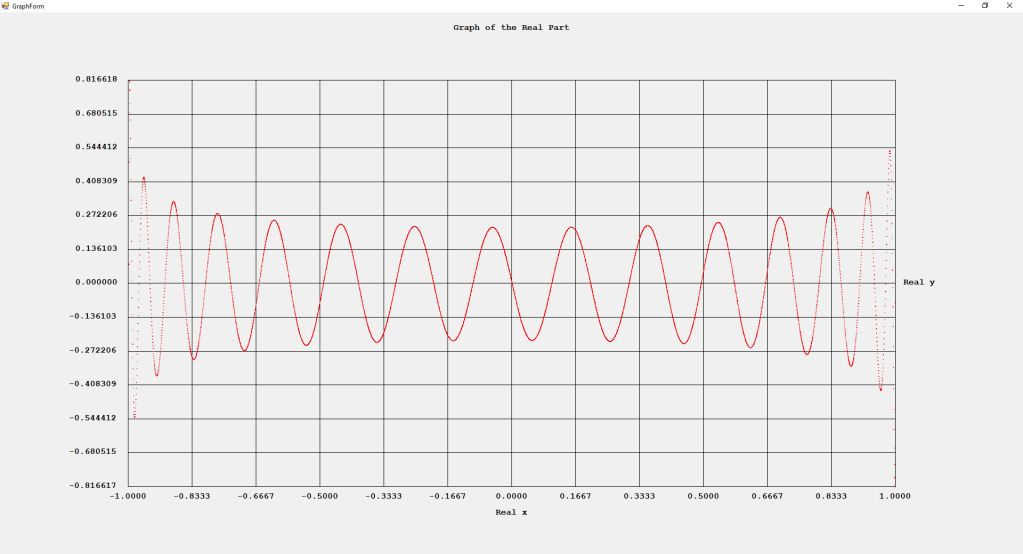
First Order Perturbation Calculation for the Helium Atom Ground State by James Pate Williams, Jr.
The first order perturbation calculation for the helium atom ground state is treated in detail in the textbook “Quantum Mechanics Third Edition” by Leonard I. Schiff pages 257 to 259. I offer a numerical algorithm for computing the electron-electron repulsion interaction which is analytically determined by Schiff and other scientists. Next is the graphical user interface for the application and its output.
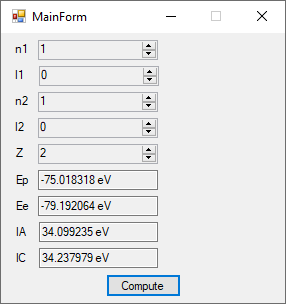
The Ep text box is the ground state energy as found by a first order perturbation computation. The Ee text box is the experimental ground state energy. The IA text box is the analytic electron-electron repulsion interaction determined by Schiff and other quantum mechanics researchers. The IC text box is my numerical contribution. All the energies are in electron volts.
The application source code are the next items in this blog.
Experimental Computational Quantum Chemistry and Quantum Mechanics by James Pate Williams, Jr.
In my current return to my youthful dual interests in quantum chemistry and quantum mechanics that occupied much of my time in the 1960s, 1970s and 1980s, I am now using my knowledge of experimental numerical analysis. My interest in computer science and numerical analysis began in the summer of 1976 while I was a chemistry student at my local college namely LaGrange College in LaGrange, Georgia. As a child and teenager I was very interested in several disciplines of physics: classical mechanics, quantum mechanics, and the theories of special and general relativity. Later I added to my knowledge toolkit some tidbits of statistical mechanics and statistical thermodynamics.
This blog entry will explore the wonderful world of the hydrogenic atom which used to known by the moniker, hydrogen-like atom. The most well known isotope of hydrogen has one electron and one proton and its atomic number is 1 and it is sometimes denoted by the letter and numeral Z = 1. Of course, there are multiple other isotopes of hydrogen including deuterium (one proton and one neutron) and tritium (one proton and two neutrons). Hydrogen is the only atom whose wave functions both non-relativistic (see Erwin Schrödinger) and relativistic (view Paul Adrian Maurice Dirac) have analytic close formed solutions. Hydrogen is the most abundant chemical element on Earth and in the universe. The stars initially use a hydrogen plasma as a nuclear fuel to create more massive atomic ions and release massive amounts of nuclear fusion energy.
Way back in the 1920s Erwin Schrödinger decided to apply his work in wave hydrology to the newly found branch of physics known as quantum theory and quantum mechanics. From his work the branch of quantum mechanics known as wave quantum mechanics evolved. This branch was as important as another competing theory of quantum mechanics known as matrix quantum mechanics that was being concurrently developed by Werner Heisenberg. The key process in the derivation of a Schrödinger equation for any time independent scenario is to apply the first quantization rules to a valid classical Hamiltonian. The classical Hamiltonian is the total energy of a system and is the sum of the kinetic energy and the potential energy. The classical Hamiltonian for the hydrogen-like atom is shown in equation (1).
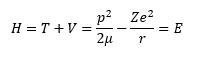
The first quantization rule is to apply the conversion from a classical momentum vector to a momentum quantum mechanical operator using the equation (2).
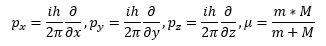
The lower case m is the mass of the electron and the upper case M is the mass of the atomic nucleus which is the Z times the proton mass plus the number of neutrons times the neutron mass. The Greek letter mu is the reduced mass of the hydrogen-like system. The italic i is the imaginary unit that is the square root of the number -1. The transcendental number pi is represented by the Greek letter pi and has the truncated real number value of 3.1415926535897932384626433832795. Schrödinger plugged Equation (2) into Equation (1) and found a three-dimensional Cartesian coordinate second order partial differential equation (3) that used the operator discovered by the mathematician Laplace.
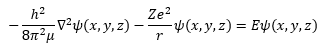
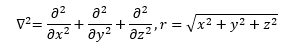
In equation (4) the first partial differential operator is the Laplace operator which is the vector inner product of the three-dimensional Cartesian gradient operator from vector analysis. The scalar r in equation (4) is the Euclidean distance from the electron to the nucleus. The Greek letter psi (“pitchfork”) in equation (3) is the illustrious and elusive wave function.
The first thing that struck Schrödinger was that the equation (3) that he derived by much thought was unfortunately not a separable partial differential equation in three-dimensional Cartesian coordinates, however, he next applied a coordinate coordinate transformation from three-dimensional Cartesian coordinates to three dimensional spherical polar equations specified by the equations in the following PDF with some derivations.
The wave function for the hydrogen-like atom is dependent on the associated Laguerre polynomials and the spherical harmonics that dependent upon the associated Legendre functions.
https://mathworld.wolfram.com/AssociatedLaguerrePolynomial.html
https://www.sciencedirect.com/topics/mathematics/associated-legendre-function
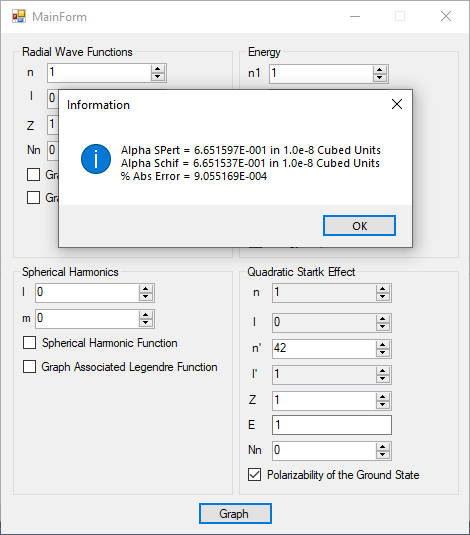
I created a useful C# desktop application that allows some graphical exploration of the hydrogen-like atom. Here is the graphical user interface.
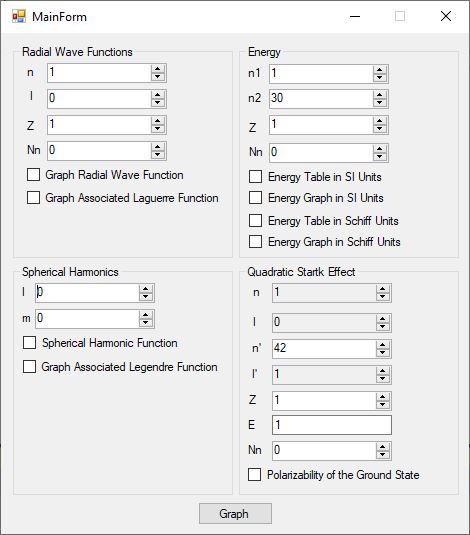
The PDF file below are graphs for the radial wave functions for the hydrogen-like atom for n = 1 to 8 which are the s-orbitals.
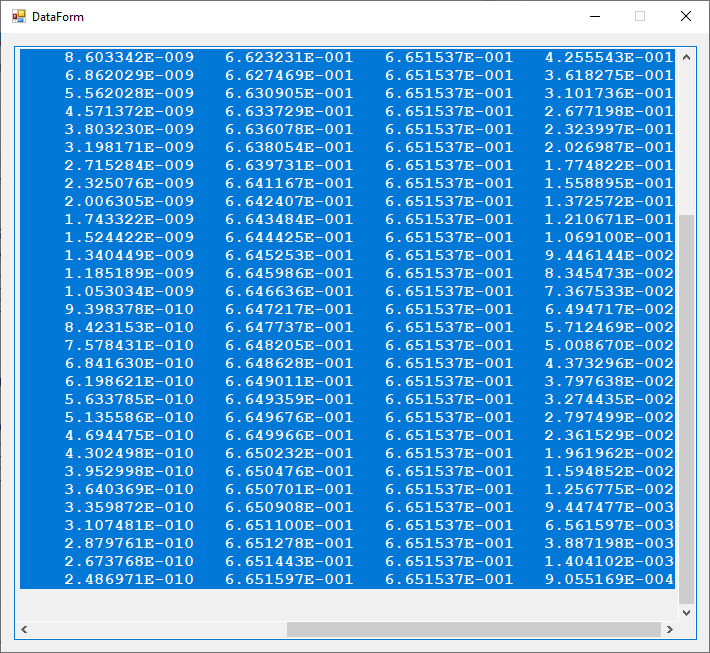
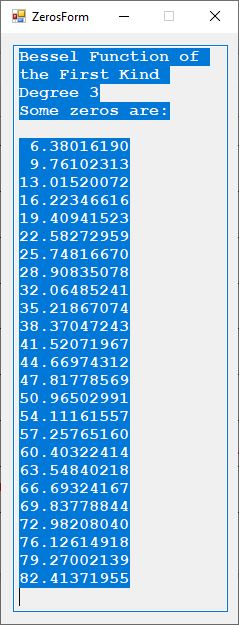
Bessel Functions of the First and Second Kind and Their Derivatives and Some Zeros for n = 3 by James Pate Williams, Jr.







Three Ways of Computing a Few Digits of Pi by James Pate Williams, Jr.
I wrote a short C++ program to calculate a few digits of pi, a famous transcendental number. The algorithms are as follows:
- Monte Carlo Method
- Leibniz’s Infinite Series
- Nilakantha’s Infinite Series
First the results then the C++ source code listing.



Steady State Temperature in an Insulated Cylinder by James Pate Williams, Jr.



using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Windows.Forms;
namespace SteadyStateTempCylinder
{
public partial class MainForm : Form
{
private double steps;
private int N, nsteps;
private BackgroundWorker bw;
private DateTime dt0;
private List<PotPoint> pts;
private double f(double r)
{
return r;
}
private double g(double r)
{
return r * r;
}
public MainForm()
{
InitializeComponent();
comboBox1.SelectedIndex = 0;
comboBox2.SelectedIndex = 0;
comboBox3.SelectedIndex = 0;
}
private void button1_Click(object sender, EventArgs e)
{
if (button1.Text.CompareTo("&Draw") == 0)
{
N = int.Parse((string)comboBox1.SelectedItem);
nsteps = int.Parse((string)comboBox2.SelectedItem);
steps = double.Parse((string)comboBox3.SelectedItem);
bw = new BackgroundWorker();
bw.DoWork += new DoWorkEventHandler(bw_DoWork);
bw.ProgressChanged += new ProgressChangedEventHandler(bw_ProgressChanged);
bw.RunWorkerCompleted += new RunWorkerCompletedEventHandler(bw_RunWorkerCompleted);
bw.WorkerReportsProgress = true;
bw.WorkerSupportsCancellation = true;
bw.RunWorkerAsync();
while (!bw.IsBusy) { }
button1.Text = "&Stop";
textBox1.Text = string.Empty;
}
else
bw.CancelAsync();
}
private void bw_ProgressChanged(object sender, ProgressChangedEventArgs e)
{
if (e.ProgressPercentage >= 0 && e.ProgressPercentage <= 100)
progressBar1.Value = e.ProgressPercentage;
}
private void bw_RunWorkerCompleted(object sender, RunWorkerCompletedEventArgs e)
{
try
{
DateTime dt1 = DateTime.Now;
TimeSpan ts = dt1 - dt0;
DrawGraphForm dgf = new DrawGraphForm(1.0, 1.0, pts);
dgf.Show();
button1.Text = "&Draw";
progressBar1.Value = 0;
textBox1.Text = ts.Hours.ToString("D2") + ":";
textBox1.Text += ts.Minutes.ToString("D2") + ":";
textBox1.Text += ts.Seconds.ToString("D2") + ".";
textBox1.Text += ts.Milliseconds.ToString("D3");
}
catch (Exception ex)
{
MessageBox.Show(ex.ToString(), "Warning Message",
MessageBoxButtons.OK, MessageBoxIcon.Warning);
}
}
private void bw_DoWork(object sender, DoWorkEventArgs e)
{
dt0 = DateTime.Now;
double step = 1.0 / Math.Sqrt(steps);
double percent = steps / 100.0;
int total = 0;
int count = 0;
pts = new List<PotPoint>();
double r = 0.0, z = 0.0;
double umin = double.MaxValue;
double umax = double.MinValue;
SteadyStateTemp sst = new SteadyStateTemp(1.0, 1.0, N, nsteps, f, g);
while (r <= 1.0)
{
z = 0.0;
while (z <= 1.0)
{
double u = sst.u(r, z);
PotPoint pt = new PotPoint(r, z, u);
pts.Add(pt);
z += step;
count++;
if (count >= percent)
{
count = 0;
total++;
bw.ReportProgress(total);
}
if (u < umin)
umin = u;
if (u > umax)
umax = u;
}
r += step;
}
}
}
}using System;
namespace SteadyStateTempCylinder
{
class SteadyStateTemp
{
private double A, B;
private double[] Jn;
private double[] lambda;
private int N, n, nsteps;
private BesselFunctions bf;
private Func<double, double> f;
Func<double, double> g;
public SteadyStateTemp(
double A,
double B,
int N, int nsteps,
Func<double, double> f,
Func<double, double> g)
{
double[] zeros = new double[N];
this.A = A;
this.B = B;
this.N = N;
this.nsteps = nsteps;
this.f = f;
this.g = g;
Jn = new double[N + 1];
lambda = new double[N + 1];
bf = new BesselFunctions();
bf.besszeros(1, N, zeros, 1);
for (n = 1; n <= N; n++)
{
lambda[n] = zeros[n - 1];
Jn[n] = J();
}
}
private double SimpsonsRule(double lower, double upper, Func<double, double> f)
{
double h = (upper - lower) / nsteps;
double h2 = 2.0 * h;
double s = 0.0;
double t = 0.0;
double x = lower + h;
for (int i = 1; i < nsteps; i += 2)
{
s += f(x);
x += h2;
}
x = lower + h2;
for (int i = 2; i < nsteps; i += 2)
{
t += f(x);
x += h2;
}
return h * (f(lower) + 4 * s + 2 * t + f(upper)) / 3.0;
}
private double IIntegrand(double r)
{
return bf.bessj0(lambda[n] * r) * r;
}
private double I()
{
return SimpsonsRule(0.0, A, IIntegrand);
}
private double JIntegrand(double r)
{
double b0 = bf.bessj0(lambda[n] * r);
return b0 * b0 * r;
}
private double J()
{
return SimpsonsRule(0.0, A, JIntegrand);
}
private double KIntegrand(double r)
{
return bf.bessj0(lambda[n] * r) * f(r) * r;
}
private double K()
{
return SimpsonsRule(0.0, A, KIntegrand);
}
private double LIntegrand(double r)
{
return bf.bessj0(lambda[n] * r) * g(r) * r;
}
private double L()
{
return SimpsonsRule(0.0, A, LIntegrand);
}
public double u(double r, double z)
{
double sum = 0.0;
for (n = 1; n <= N; n++)
{
double denom = Math.Sinh(lambda[n] * B);
double J0 = bf.bessj0(lambda[n] * r);
double an = L() / Jn[n];
double bn = K() / Jn[n];
sum += J0 * an * Math.Sinh(lambda[n] * z) / denom;
sum += J0 * bn * Math.Sinh(lambda[n] * (B - z)) / denom;
}
return sum;
}
}
}using System;
namespace SteadyStateTempCylinder
{
class BesselFunctions
{
public double bessj0(double x)
{
if (x == 0.0) return 1.0;
if (Math.Abs(x) < 8.0)
{
int i;
double z, z2, b0, b1, b2;
double[] ar ={-0.75885e-15, 0.4125321e-13,
-0.194383469e-11, 0.7848696314e-10, -0.267925353056e-8,
0.7608163592419e-7, -0.176194690776215e-5,
0.324603288210051e-4, -0.46062616620628e-3,
0.48191800694676e-2, -0.34893769411409e-1,
0.158067102332097, -0.37009499387265, 0.265178613203337,
-0.872344235285222e-2};
x /= 8.0;
z = 2.0 * x * x - 1.0;
z2 = z + z;
b1 = b2 = 0.0;
for (i = 0; i <= 14; i++)
{
b0 = z2 * b1 - b2 + ar[i];
b2 = b1;
b1 = b0;
}
return z * b1 - b2 + 0.15772797147489;
}
else
{
double c, cosx, sinx, p0 = 0.0, q0 = 0.0;
x = Math.Abs(x);
c = 0.797884560802865 / Math.Sqrt(x);
cosx = Math.Cos(x - 0.706858347057703e1);
sinx = Math.Sin(x - 0.706858347057703e1);
besspq0(x, ref p0, ref q0);
return c * (p0 * cosx - q0 * sinx);
}
}
public double bessj1(double x)
{
if (x == 0.0) return 1.0;
if (Math.Abs(x) < 8.0)
{
int i;
double z, z2, b0, b1, b2;
double[] ar ={-0.19554e-15, 0.1138572e-13,
-0.57774042e-12, 0.2528123664e-10, -0.94242129816e-9,
0.2949707007278e-7, -0.76175878054003e-6,
0.158870192399321e-4, -0.260444389348581e-3,
0.324027018268386e-2, -0.291755248061542e-1,
0.177709117239728e0, -0.661443934134543e0,
0.128799409885768e1, -0.119180116054122e1};
x /= 8.0;
z = 2.0 * x * x - 1.0;
z2 = z + z;
b1 = b2 = 0.0;
for (i = 0; i <= 14; i++)
{
b0 = z2 * b1 - b2 + ar[i];
b2 = b1;
b1 = b0;
}
return x * (z * b1 - b2 + 0.648358770605265);
}
else
{
int sgnx;
double c, cosx, sinx, p1 = 0.0, q1 = 0.0;
sgnx = (x > 0.0) ? 1 : -1;
x = Math.Abs(x);
c = 0.797884560802865 / Math.Sqrt(x);
cosx = Math.Cos(x - 0.706858347057703e1);
sinx = Math.Sin(x - 0.706858347057703e1);
besspq1(x, ref p1, ref q1);
return sgnx * c * (p1 * sinx + q1 * cosx);
}
}
private void besspq0(double x, ref double p0, ref double q0)
{
if (x < 8.0)
{
double b, cosx, sinx, j0x = 0.0, y0 = 0.0;
b = Math.Sqrt(x) * 1.25331413731550;
bessy01(x, ref y0, ref j0x);
j0x = bessj0(x);
x -= 0.785398163397448;
cosx = Math.Cos(x);
sinx = Math.Sin(x);
p0 = b * (y0 * sinx + j0x * cosx);
q0 = b * (y0 * cosx - j0x * sinx);
}
else
{
int i;
double x2, b0, b1, b2, y;
double[] ar1 ={-0.10012e-15, 0.67481e-15, -0.506903e-14,
0.4326596e-13, -0.43045789e-12, 0.516826239e-11,
-0.7864091377e-10, 0.163064646352e-8, -0.5170594537606e-7,
0.30751847875195e-5, -0.536522046813212e-3};
double[] ar2 ={-0.60999e-15, 0.425523e-14,
-0.3336328e-13, 0.30061451e-12, -0.320674742e-11,
0.4220121905e-10, -0.72719159369e-9, 0.1797245724797e-7,
-0.74144984110606e-6, 0.683851994261165e-4};
y = 8.0 / x;
x = 2.0 * y * y - 1.0;
x2 = x + x;
b1 = b2 = 0.0;
for (i = 0; i <= 10; i++)
{
b0 = x2 * b1 - b2 + ar1[i];
b2 = b1;
b1 = b0;
}
p0 = x * b1 - b2 + 0.99946034934752;
b1 = b2 = 0.0;
for (i = 0; i <= 9; i++)
{
b0 = x2 * b1 - b2 + ar2[i];
b2 = b1;
b1 = b0;
}
q0 = (x * b1 - b2 - 0.015555854605337) * y;
}
}
private void besspq1(double x, ref double p1, ref double q1)
{
if (x < 8.0)
{
double b, cosx, sinx, j1x = 0.0, y1 = 0.0;
b = Math.Sqrt(x) * 1.25331413731550;
bessy01(x, ref j1x, ref y1);
j1x = bessj1(x);
x -= 0.785398163397448;
cosx = Math.Cos(x);
sinx = Math.Sin(x);
p1 = b * (j1x * sinx - y1 * cosx);
q1 = b * (j1x * cosx + y1 * sinx);
}
else
{
int i;
double x2, b0, b1, b2, y;
double[] ar1 ={0.10668e-15, -0.72212e-15, 0.545267e-14,
-0.4684224e-13, 0.46991955e-12, -0.570486364e-11,
0.881689866e-10, -0.187189074911e-8, 0.6177633960644e-7,
-0.39872843004889e-5, 0.89898983308594e-3};
double[] ar2 ={-0.10269e-15, 0.65083e-15, -0.456125e-14,
0.3596777e-13, -0.32643157e-12, 0.351521879e-11,
-0.4686363688e-10, 0.82291933277e-9, -0.2095978138408e-7,
0.91386152579555e-6, -0.96277235491571e-4};
y = 8.0 / x;
x = 2.0 * y * y - 1.0;
x2 = x + x;
b1 = b2 = 0.0;
for (i = 0; i <= 10; i++)
{
b0 = x2 * b1 - b2 + ar1[i];
b2 = b1;
b1 = b0;
}
p1 = x * b1 - b2 + 1.0009030408600137;
b1 = b2 = 0.0;
for (i = 0; i <= 10; i++)
{
b0 = x2 * b1 - b2 + ar2[i];
b2 = b1;
b1 = b0;
}
q1 = (x * b1 - b2 + 0.46777787069535e-1) * y;
}
}
private void bessy01(double x, ref double y0, ref double y1)
{
if (x < 8.0)
{
int i;
double z, z2, c, lnx, b0, b1, b2;
double[] ar1 ={0.164349e-14, -0.8747341e-13,
0.402633082e-11, -0.15837552542e-9, 0.524879478733e-8,
-0.14407233274019e-6, 0.32065325376548e-5,
-0.563207914105699e-4, 0.753113593257774e-3,
-0.72879624795521e-2, 0.471966895957634e-1,
-0.177302012781143, 0.261567346255047,
0.179034314077182, -0.274474305529745};
double[] ar2 ={0.42773e-15, -0.2440949e-13,
0.121143321e-11, -0.5172121473e-10, 0.187547032473e-8,
-0.5688440039919e-7, 0.141662436449235e-5,
-0.283046401495148e-4, 0.440478629867099e-3,
-0.51316411610611e-2, 0.423191803533369e-1,
-0.226624991556755, 0.675615780772188,
-0.767296362886646, -0.128697384381350};
c = 0.636619772367581;
lnx = c * Math.Log(x);
c /= x;
x /= 8.0;
z = 2.0 * x * x - 1.0;
z2 = z + z;
b1 = b2 = 0.0;
for (i = 0; i <= 14; i++)
{
b0 = z2 * b1 - b2 + ar1[i];
b2 = b1;
b1 = b0;
}
y0 = lnx * bessj0(8.0 * x) + z * b1 - b2 - 0.33146113203285e-1;
b1 = b2 = 0.0;
for (i = 0; i <= 14; i++)
{
b0 = z2 * b1 - b2 + ar2[i];
b2 = b1;
b1 = b0;
}
y1 = lnx * bessj1(8.0 * x) - c + x * (z * b1 - b2 + 0.2030410588593425e-1);
}
else
{
double c, cosx, sinx, p0 = 0.0, q0 = 0.0, p1 = 0.0, q1 = 0.0;
c = 0.797884560802865 / Math.Sqrt(x);
besspq0(x, ref p0, ref q0);
besspq1(x, ref p1, ref q1);
x -= 0.706858347057703e1;
cosx = Math.Cos(x);
sinx = Math.Sin(x);
y0 = c * (p0 * sinx + q0 * cosx);
y1 = c * (q1 * sinx - p1 * cosx);
}
}
private double recipgamma(double x, ref double odd, ref double even)
{
int i;
double alfa, beta, x2;
double[] b = new double[13];
b[1] = -0.283876542276024; b[2] = -0.076852840844786;
b[3] = 0.001706305071096; b[4] = 0.001271927136655;
b[5] = 0.000076309597586; b[6] = -0.000004971736704;
b[7] = -0.000000865920800; b[8] = -0.000000033126120;
b[9] = 0.000000001745136; b[10] = 0.000000000242310;
b[11] = 0.000000000009161; b[12] = -0.000000000000170;
x2 = x * x * 8.0;
alfa = -0.000000000000001;
beta = 0.0;
for (i = 12; i >= 2; i -= 2)
{
beta = -(alfa * 2.0 + beta);
alfa = -beta * x2 - alfa + b[i];
}
even = (beta / 2.0 + alfa) * x2 - alfa + 0.921870293650453;
alfa = -0.000000000000034;
beta = 0.0;
for (i = 11; i >= 1; i -= 2)
{
beta = -(alfa * 2.0 + beta);
alfa = -beta * x2 - alfa + b[i];
}
odd = (alfa + beta) * 2.0;
return odd * x + even;
}
private void bessya01(double a, double x, ref double ya, ref double ya1)
{
if (a == 0.0)
{
bessy01(x, ref ya, ref ya1);
}
else
{
bool rec, rev;
int n, na;
double b, c, d, e, f, g, h = 0.0, p = 0.0, pi, q = 0.0, r, s;
pi = Math.PI;
na = (int)Math.Floor(a + 0.5);
rec = (a >= 0.5);
rev = (a < -0.5);
if (rev || rec) a -= na;
if (a == -0.5)
{
p = Math.Sqrt(2.0 / pi / x);
f = p * Math.Sin(x);
g = -p * Math.Cos(x);
}
else if (x < 3.0)
{
b = x / 2.0;
d = -Math.Log(b);
e = a * d;
c = (Math.Abs(a) < 1.0e-8) ? 1.0 / pi : a / Math.Sin(a * pi);
s = (Math.Abs(e) < 1.0e-8) ? 1.0 : Math.Sinh(e) / e;
e = Math.Exp(e);
g = recipgamma(a, ref p, ref q) * e;
e = (e + 1.0 / e) / 2.0;
f = 2.0 * c * (p * e + q * s * d);
e = a * a;
p = g * c;
q = 1.0 / g / pi;
c = a * pi / 2.0;
r = (Math.Abs(c) < 1.0e-8) ? 1.0 : Math.Sin(c) / c;
r *= pi * c * r;
c = 1.0;
d = -b * b;
ya = f + r * q;
ya1 = p;
n = 1;
do
{
f = (f * n + p + q) / (n * n - e);
c = c * d / n;
p /= (n - a);
q /= (n + a);
g = c * (f + r * q);
h = c * p - n * g;
ya += g;
ya1 += h;
n++;
} while (Math.Abs(g / (1.0 + Math.Abs(ya))) + Math.Abs(h / (1.0 + Math.Abs(ya1))) >
1.0e-15);
f = -ya;
g = -ya1 / b;
}
else
{
b = x - pi * (a + 0.5) / 2.0;
c = Math.Cos(b);
s = Math.Sin(b);
d = Math.Sqrt(2.0 / x / pi);
besspqa01(a, x, ref p, ref q, ref b, ref h);
f = d * (p * s + q * c);
g = d * (h * s - b * c);
}
if (rev)
{
x = 2.0 / x;
na = -na - 1;
for (n = 0; n <= na; n++)
{
h = x * (a - n) * f - g;
g = f;
f = h;
}
}
else if (rec)
{
x = 2.0 / x;
for (n = 1; n <= na; n++)
{
h = x * (a + n) * g - f;
f = g;
g = h;
}
}
ya = f;
ya1 = g;
}
}
private int start(double x, int n, int t)
{
int s;
double p, q, r, y;
s = 2 * t - 1;
p = 36.0 / x - t;
r = n / x;
if (r > 1.0 || t == 1)
{
q = Math.Sqrt(r * r + s);
r = r * Math.Log(q + r) - q;
}
else
r = 0.0;
q = 18.0 / x + r;
r = (p > q) ? p : q;
p = Math.Sqrt(2.0 * (t + r));
p = x * ((1.0 + r) + p) / (1.0 + p);
y = 0.0;
q = y;
do
{
y = p;
p /= x;
q = Math.Sqrt(p * p + s);
p = x * (r + q) / Math.Log(p + q);
q = y;
} while (p > q || p < q - 1.0);
return (t == 1) ? (int)Math.Floor(p + 1.0) : -(int)Math.Floor(-p / 2.0) * 2;
}
public void bessj(double x, int n, double[] j)
{
if (x == 0.0)
{
j[0] = 1.0;
for (; n >= 1; n--) j[n] = 0.0;
}
else
{
int l, m, nu, signx;
double x2, r, s;
signx = (x > 0.0) ? 1 : -1;
x = Math.Abs(x);
r = s = 0.0;
x2 = 2.0 / x;
l = 0;
nu = start(x, n, 0);
for (m = nu; m >= 1; m--)
{
r = 1.0 / (x2 * m - r);
l = 2 - l;
s = r * (l + s);
if (m <= n) j[m] = r;
}
j[0] = r = 1.0 / (1.0 + s);
for (m = 1; m <= n; m++) r = j[m] *= r;
if (signx < 0.0)
for (m = 1; m <= n; m += 2) j[m] = -j[m];
}
}
private void spherbessj(double x, int n, double[] j)
{
if (x == 0.0)
{
j[0] = 1.0;
for (; n >= 1; n--) j[n] = 0.0;
}
else if (n == 0)
{
double x2;
if (Math.Abs(x) < 0.015)
{
x2 = x * x / 6.0;
j[0] = 1.0 + x2 * (x2 * 0.3 - 1.0);
}
else
j[0] = Math.Sin(x) / x;
}
else
{
int m;
double r, s;
r = 0.0;
m = start(x, n, 0);
for (; m >= 1; m--)
{
r = 1.0 / ((m + m + 1) / x - r);
if (m <= n) j[m] = r;
}
if (x < 0.015)
{
s = x * x / 6.0;
j[0] = r = s * (s * 0.3 - 1.0) + 1.0;
}
else
j[0] = r = Math.Sin(x) / x;
for (m = 1; m <= n; m++) r = j[m] *= r;
}
}
private double loggamma(double x)
{
int i;
double r, x2, y, f, u0, u1, u, z;
double[] b = new double[19];
if (x > 13.0)
{
r = 1.0;
while (x <= 22.0)
{
r /= x;
x += 1.0;
}
x2 = -1.0 / (x * x);
r = Math.Log(r);
return Math.Log(x) * (x - 0.5) - x + r + 0.918938533204672 +
(((0.595238095238095e-3 * x2 + 0.793650793650794e-3) * x2 +
0.277777777777778e-2) * x2 + 0.833333333333333e-1) / x;
}
else
{
f = 1.0;
u0 = u1 = 0.0;
b[1] = -0.0761141616704358; b[2] = 0.0084323249659328;
b[3] = -0.0010794937263286; b[4] = 0.0001490074800369;
b[5] = -0.0000215123998886; b[6] = 0.0000031979329861;
b[7] = -0.0000004851693012; b[8] = 0.0000000747148782;
b[9] = -0.0000000116382967; b[10] = 0.0000000018294004;
b[11] = -0.0000000002896918; b[12] = 0.0000000000461570;
b[13] = -0.0000000000073928; b[14] = 0.0000000000011894;
b[15] = -0.0000000000001921; b[16] = 0.0000000000000311;
b[17] = -0.0000000000000051; b[18] = 0.0000000000000008;
if (x < 1.0)
{
f = 1.0 / x;
x += 1.0;
}
else
while (x > 2.0)
{
x -= 1.0;
f *= x;
}
f = Math.Log(f);
y = x + x - 3.0;
z = y + y;
for (i = 18; i >= 1; i--)
{
u = u0;
u0 = z * u0 + b[i] - u1;
u1 = u;
}
return (u0 * y + 0.491415393029387 - u1) * (x - 1.0) * (x - 2.0) + f;
}
}
private double gamma(double x)
{
int inv;
double y, s, f = 0.0, g, odd = 0.0, even = 0.0;
if (x < 0.5)
{
y = x - Math.Floor(x / 2.0) * 2;
s = Math.PI;
if (y >= 1.0)
{
s = -s;
y = 2.0 - y;
}
if (y >= 0.5) y = 1.0 - y;
inv = 1;
x = 1.0 - x;
f = s / Math.Sin(3.14159265358979 * y);
}
else
inv = 0;
if (x > 22.0)
g = Math.Exp(loggamma(x));
else
{
s = 1.0;
while (x > 1.5)
{
x = x - 1.0;
s *= x;
}
g = s / recipgamma(1.0 - x, ref odd, ref even);
}
return (inv == 1 ? f / g : g);
}
private void bessjaplusn(double a, double x, int n, double[] ja)
{
if (x == 0.0)
{
ja[0] = (a == 0.0) ? 1.0 : 0.0;
for (; n >= 1; n--) ja[n] = 0.0;
}
else if (a == 0.0)
{
bessj(x, n, ja);
}
else if (a == 0.5)
{
double s;
s = Math.Sqrt(x) * 0.797884560802865;
spherbessj(x, n, ja);
for (; n >= 0; n--) ja[n] *= s;
}
else
{
int k, m, nu;
double a2, x2, r, s, l, labda;
l = 1.0;
nu = start(x, n, 0);
for (m = 1; m <= nu; m++) l = l * (m + a) / (m + 1);
r = s = 0.0;
x2 = 2.0 / x;
k = -1;
a2 = a + a;
for (m = nu + nu; m >= 1; m--)
{
r = 1.0 / (x2 * (a + m) - r);
if (k == 1)
labda = 0.0;
else
{
l = l * (m + 2) / (m + a2);
labda = l * (m + a);
}
s = r * (labda + s);
k = -k;
if (m <= n) ja[m] = r;
}
ja[0] = r = 1.0 / gamma(1.0 + a) / (1.0 + s) / Math.Pow(x2, a);
for (m = 1; m <= n; m++) r = ja[m] *= r;
}
}
private void besspqa01(double a, double x, ref double pa, ref double qa,
ref double pa1, ref double qa1)
{
if (a == 0.0)
{
besspq0(x, ref pa, ref qa);
besspq1(x, ref pa1, ref qa1);
}
else
{
bool rec, rev;
int n, na = 0;
double b, pi, p0, q0;
pi = Math.PI;
rev = a < -0.5;
if (rev) a = -a - 1.0;
rec = a >= 0.5;
if (rec)
{
na = (int)Math.Floor(a + 0.5);
a -= na;
}
if (a == -0.5)
{
pa = pa1 = 1.0;
qa = qa1 = 0.0;
}
else if (x >= 3.0)
{
double c, d, e, f, g, p, q, r, s, temp;
c = 0.25 - a * a;
b = x + x;
f = r = 1.0;
g = -x;
s = 0.0;
temp = x * Math.Cos(a * pi) / pi * 1.0e15;
e = temp * temp;
n = 2;
do
{
d = (n - 1 + c / n);
p = (2 * n * f + b * g - d * r) / (n + 1);
q = (2 * n * g - b * f - d * s) / (n + 1);
r = f;
f = p;
s = g;
g = q;
n++;
} while ((p * p + q * q) * n * n < e);
e = f * f + g * g;
p = (r * f + s * g) / e;
q = (s * f - r * g) / e;
f = p;
g = q;
n--;
while (n > 0)
{
r = (n + 1) * (2.0 - p) - 2.0;
s = b + (n + 1) * q;
d = (n - 1 + c / n) / (r * r + s * s);
p = d * r;
q = d * s;
e = f;
f = p * (e + 1.0) - g * q;
g = q * (e + 1.0) + p * g;
n--;
}
f += 1.0;
d = f * f + g * g;
pa = f / d;
qa = -g / d;
d = a + 0.5 - p;
q += x;
pa1 = (pa * q - qa * d) / x;
qa1 = (qa * q + pa * d) / x;
}
else
{
double c, s, chi, ya = 0.0, ya1 = 0.0;
double[] ja = new double[2];
b = Math.Sqrt(pi * x / 2.0);
chi = x - pi * (a / 2.0 + 0.25);
c = Math.Cos(chi);
s = Math.Sin(chi);
bessya01(a, x, ref ya, ref ya1);
bessjaplusn(a, x, 1, ja);
pa = b * (ya * s + c * ja[0]);
qa = b * (c * ya - s * ja[0]);
pa1 = b * (s * ja[1] - c * ya1);
qa1 = b * (c * ja[1] + s * ya1);
}
if (rec)
{
x = 2.0 / x;
b = (a + 1.0) * x;
for (n = 1; n <= na; n++)
{
p0 = pa - qa1 * b;
q0 = qa + pa1 * b;
pa = pa1;
pa1 = p0;
qa = qa1;
qa1 = q0;
b += x;
}
}
if (rev)
{
p0 = pa1;
pa1 = pa;
pa = p0;
q0 = qa1;
qa1 = qa;
qa = q0;
}
}
}
public void besszeros(double a, int n, double[] z, int d)
{
int j, s;
double aa, a2, b, bb, c, chi, co, mu, mu2, mu3, mu4, p, pi, pa = 0.0, pa1 = 0.0, p0, p1, pp1,
q, qa = 0.0, qa1 = 0.0, q1, qq1, ro, si, t, tt, u, v, w, x, xx, x4, y, yy, fi;
pi = Math.PI;
aa = a * a;
mu = 4.0 * aa;
mu2 = mu * mu;
mu3 = mu * mu2;
mu4 = mu2 * mu2;
if (d < 3)
{
p = 7.0 * mu - 31.0;
p0 = mu - 1.0;
p1 = 4.0 * (253.0 * mu2 - 3722.0 * mu + 17869.0) / 15.0 / p * p0;
q1 = 8.0 * (83.0 * mu2 - 982.0 * mu + 3779.0) / 5.0 / p;
}
else
{
p = 7.0 * mu2 + 82.0 * mu - 9.0;
p0 = mu + 3.0;
p1 = (4048.0 * mu4 + 131264.0 * mu3 - 221984.0 * mu2 -
417600.0 * mu + 1012176.0) / 60.0 / p;
q1 = 1.6 * (83.0 * mu3 + 2075.0 * mu2 - 3039.0 * mu + 3537.0) / p;
}
t = (d == 1 || d == 4) ? 0.25 : 0.75;
tt = 4.0 * t;
if (d < 3)
{
pp1 = 5.0 / 48.0;
qq1 = -5.0 / 36.0;
}
else
{
pp1 = -7.0 / 48.0;
qq1 = 35.0 / 288.0;
}
y = 3.0 * pi / 8.0;
bb = (a >= 3.0) ? Math.Pow(a, -2.0 / 3.0) : 0.0;
for (s = 1; s <= n; s++)
{
if (a == 0.0 && s == 1 && d == 3)
{
x = 0.0;
j = 0;
}
else
{
if (s >= 3.0 * a - 8.0)
{
b = (s + a / 2.0 - t) * pi;
c = 1.0 / b / b / 64.0;
x = b - 1.0 / b / 8.0 * (p0 - p1 * c) / (1.0 - q1 * c);
}
else
{
if (s == 1)
x = ((d == 1) ? -2.33811 : ((d == 2) ? -1.17371 :
((d == 3) ? -1.01879 : -2.29444)));
else
{
x = y * (4.0 * s - tt);
v = 1.0 / x / x;
x = -Math.Pow(x, 2.0 / 3.0) * (1.0 + v * (pp1 + qq1 * v));
}
u = x * bb;
yy = 2.0 / 3.0 * Math.Pow(-u, 1.5);
if (yy == 0.0)
fi = 0.0;
else if (yy > 1.0e5)
fi = 1.570796;
else
{
double r, pp;
if (yy < 1.0)
{
p = Math.Pow(3.0 * yy, 1.0 / 3.0);
pp = p * p;
p *= (1.0 + pp * (-210.0 + pp * (27.0 - 2.0 * pp)) / 1575.0);
}
else
{
p = 1.0 / (yy + 1.570796);
pp = p * p;
p = 1.570796 - p * (1.0 + pp * (2310.0 + pp * (3003.0 + pp *
(4818.0 + pp * (8591.0 + pp * 16328.0)))) / 3465.0);
}
pp = (yy + p) * (yy + p);
r = (p - Math.Atan(p + yy)) / pp;
fi = p - (1.0 + pp) * r * (1.0 + r / (p + yy));
}
v = fi;
w = 1.0 / Math.Cos(v);
xx = 1.0 - w * w;
c = Math.Sqrt(u / xx);
x = w * (a + c / a / u * ((d < 3) ?
-5.0 / 48.0 / u - c * (-5.0 / 24.0 / xx + 1.0 / 8.0) :
7.0 / 48.0 / u + c * (-7.0 / 24.0 / xx + 3.0 / 8.0)));
}
j = 0;
do
{
xx = x * x;
x4 = xx * xx;
a2 = aa - xx;
besspqa01(a, x, ref pa, ref qa, ref pa1, ref qa1);
chi = x - pi * (a / 2.0 + 0.25);
si = Math.Sin(chi);
co = Math.Cos(chi);
ro = ((d == 1) ? (pa * co - qa * si) / (pa1 * si + qa1 * co) :
((d == 2) ? (pa * si + qa * co) / (qa1 * si - pa1 * co) :
((d == 3) ? a / x - (pa1 * si + qa1 * co) / (pa * co - qa * si) :
a / x - (qa1 * si - pa1 * co) / (pa * si + qa * co))));
j++;
if (d < 3)
{
u = ro;
p = (1.0 - 4.0 * a2) / 6.0 / x / (2.0 * a + 1.0);
q = (2.0 * (xx - mu) - 1.0 - 6.0 * a) / 3.0 / x / (2.0 * a + 1.0);
}
else
{
u = -xx * ro / a2;
v = 2.0 * x * a2 / (aa + xx) / 3.0;
w = a2 * a2 * a2;
q = v * (1.0 + (mu2 + 32.0 * mu * xx + 48.0 * x4) / 32.0 / w);
p = v * (1.0 + (-mu2 + 40.0 * mu * xx + 48.0 * x4) / 64.0 / w);
}
w = u * (1.0 + p * ro) / (1.0 + q * ro);
x += w;
} while (Math.Abs(w / x) > 1.0e-13 && j < 5);
}
z[s - 1] = x;
}
}
}
}using System;
using System.Collections.Generic;
using System.Drawing;
using System.Windows.Forms;
namespace SteadyStateTempCylinder
{
public partial class DrawGraphForm : Form
{
private const double epsilon = 1.0e-2;
private double xMax;
private double yMax;
private int n;
private Brush brush;
private Brush potBrush;
private Font font;
private Pen pen1, pen2;
private List<PotPoint> pts;
public DrawGraphForm(
double xMax,
double yMax,
List<PotPoint> pts)
{
InitializeComponent();
this.xMax = xMax;
this.yMax = yMax;
this.pts = pts;
n = pts.Count;
brush = new SolidBrush(Color.Black);
potBrush = new SolidBrush(Color.Red);
pen1 = new Pen(Color.Black);
pen2 = new Pen(Color.Blue);
font = new Font("Courier New", 12f, FontStyle.Bold);
panel1.Paint += new PaintEventHandler(PanelPaintHandler);
}
private void DrawGraph(float u0, float v0,
float u1, float v1,
Graphics g)
{
try
{
float xMin = u0;
float yMin = v0;
float xMax = u1;
float yMax = v1;
float xSpan = xMax - xMin;
float ySpan = yMax - yMin;
float deltaX = xSpan / 8.0f;
float deltaY = ySpan / 8.0f;
float height = panel1.Height;
float width = panel1.Width;
float sx0 = 2f * width / 16f;
float sx1 = 14f * width / 16f;
float sy0 = 2f * height / 16f;
float sy1 = 14f * height / 16f;
float xSlope = (sx1 - sx0) / xSpan;
float xInter = sx0 - xSlope * xMin;
float ySlope = (sy0 - sy1) / ySpan;
float yInter = sy0 - ySlope * yMax;
float x = xMin;
float y = yMin;
string fTitle = "Graph of Constant u";
float w = g.MeasureString(fTitle, font).Width;
float h = g.MeasureString(fTitle, font).Height;
g.DrawString(fTitle, font, brush,
(width - w) / 2f, h);
string xTitle = "r";
w = g.MeasureString(xTitle, font).Width;
g.DrawString(xTitle, font, brush,
sx0 + (sx1 - sx0 - w) / 2f, sy1 + h + h);
string yTitle = "z";
w = g.MeasureString(yTitle, font).Width;
g.DrawString(yTitle, font, brush,
sx1 + w / 5f, sy0 + (sy1 - sy0) / 2f - h / 2f);
int i = 0;
while (i <= 8)
{
float sx = xSlope * x + xInter;
string s = string.Format("{0,5:0.00}", x);
g.DrawLine(pen1, sx, sy0, sx, sy1);
w = g.MeasureString(s, font).Width;
g.DrawString(s, font, brush,
sx - w / 2, sy1 + h / 2f);
x += deltaX;
i++;
}
i = 0;
while (i <= 8)
{
float sy = ySlope * y + yInter;
string s = string.Format("{0,5:0.00}", y);
w = g.MeasureString(s, font).Width;
g.DrawLine(pen1, sx0, sy, sx1, sy);
g.DrawString(s, font, brush,
sx0 - w - w / 5f, sy - h / 2f);
y += deltaY;
i++;
}
g.Clip = new Region(new RectangleF(
sx0, sy0, (sx1 - sx0), (sy1 - sy0)));
for (i = 0; i < n; i++)
{
float px = (float)pts[i].X;
float py = (float)pts[i].Y;
float pu = (float)pts[i].U;
if (Math.Abs(pu + 0.05) < epsilon ||
Math.Abs(pu + 0.10) < epsilon ||
Math.Abs(pu + 0.15) < epsilon ||
Math.Abs(pu + 0.20) < epsilon ||
Math.Abs(pu + 0.25) < epsilon ||
Math.Abs(pu + 0.30) < epsilon ||
Math.Abs(pu + 0.35) < epsilon ||
Math.Abs(pu + 0.40) < epsilon ||
Math.Abs(pu + 0.45) < epsilon ||
Math.Abs(pu + 0.50) < epsilon ||
Math.Abs(pu + 0.55) < epsilon ||
Math.Abs(pu + 0.60) < epsilon ||
Math.Abs(pu + 0.55) < epsilon ||
Math.Abs(pu + 0.70) < epsilon ||
Math.Abs(pu + 0.75) < epsilon ||
Math.Abs(pu + 0.80) < epsilon ||
Math.Abs(pu + 0.85) < epsilon ||
Math.Abs(pu + 0.90) < epsilon ||
Math.Abs(pu + 0.95) < epsilon ||
Math.Abs(pu - 0.05) < epsilon ||
Math.Abs(pu - 0.10) < epsilon ||
Math.Abs(pu - 0.15) < epsilon ||
Math.Abs(pu - 0.20) < epsilon ||
Math.Abs(pu - 0.25) < epsilon ||
Math.Abs(pu - 0.30) < epsilon ||
Math.Abs(pu - 0.35) < epsilon ||
Math.Abs(pu - 0.40) < epsilon ||
Math.Abs(pu - 0.45) < epsilon ||
Math.Abs(pu - 0.50) < epsilon ||
Math.Abs(pu - 0.55) < epsilon ||
Math.Abs(pu - 0.60) < epsilon ||
Math.Abs(pu - 0.55) < epsilon ||
Math.Abs(pu - 0.70) < epsilon ||
Math.Abs(pu - 0.75) < epsilon ||
Math.Abs(pu - 0.80) < epsilon ||
Math.Abs(pu - 0.85) < epsilon ||
Math.Abs(pu - 0.90) < epsilon ||
Math.Abs(pu - 0.95) < epsilon)
{
float sx = xSlope * px + xInter;
float sy = ySlope * py + yInter;
g.FillEllipse(potBrush, (float)sx, (float)sy, 2.0f, 2.0f);
}
}
}
catch (Exception ex)
{
MessageBox.Show(ex.ToString(), "Warning Message",
MessageBoxButtons.OK, MessageBoxIcon.Warning);
}
}
private void LayOutTheForm()
{
// layout the panel
int w = ClientSize.Width;
int h = ClientSize.Height;
panel1.Width = w;
panel1.Height = h;
panel1.Location = new Point(0, 0);
panel1.Invalidate();
}
protected void PanelPaintHandler(object sender, PaintEventArgs pa)
{
DrawGraph((float)0.0, (float)0.0, (float)xMax, (float)yMax, pa.Graphics);
}
protected override void OnResize(EventArgs ea)
{
LayOutTheForm();
}
}
}using System;
namespace SteadyStateTempCylinder
{
public class PotPoint : IComparable
{
private double x, y, u;
public double X
{
get
{
return x;
}
set
{
x = value;
}
}
public double Y
{
get
{
return y;
}
set
{
y = value;
}
}
public double U
{
get
{
return u;
}
set
{
u = value;
}
}
public PotPoint(double x, double y, double u)
{
this.x = x;
this.y = y;
this.u = u;
}
public int CompareTo(object obj)
{
if (obj == null)
return 1;
PotPoint pp = (PotPoint)obj;
if (u > pp.u)
return 1;
else if (u == pp.u)
return 0;
else
return -1;
}
}
}