Category: Rudimentary Crypto Systems

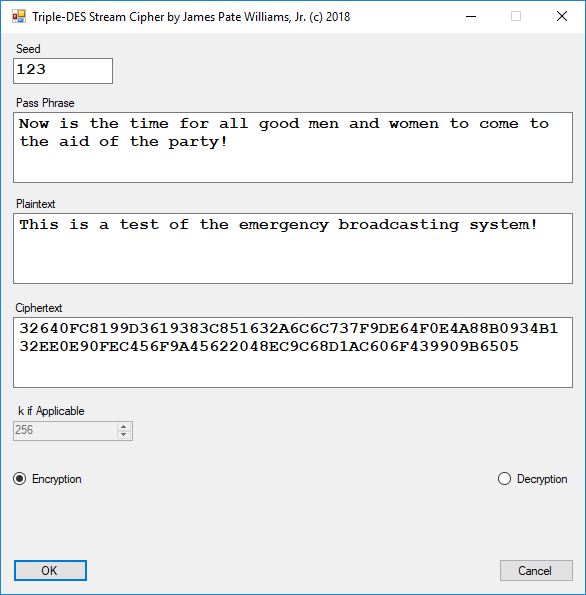
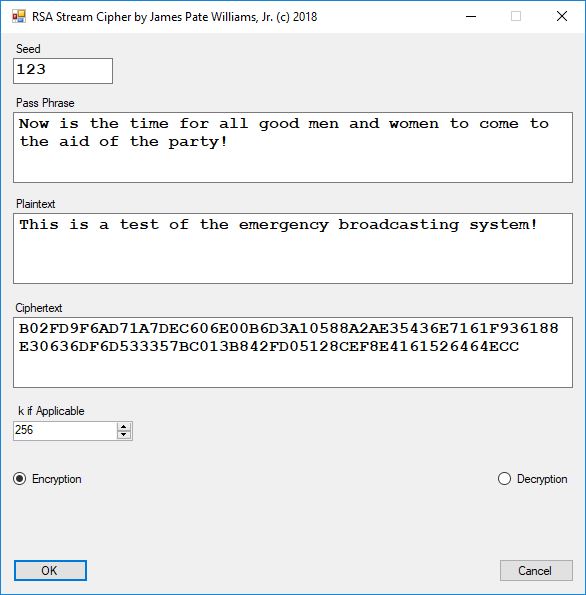
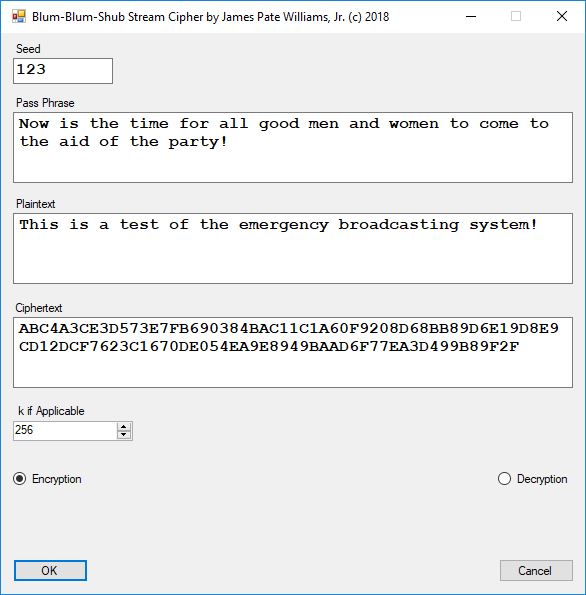
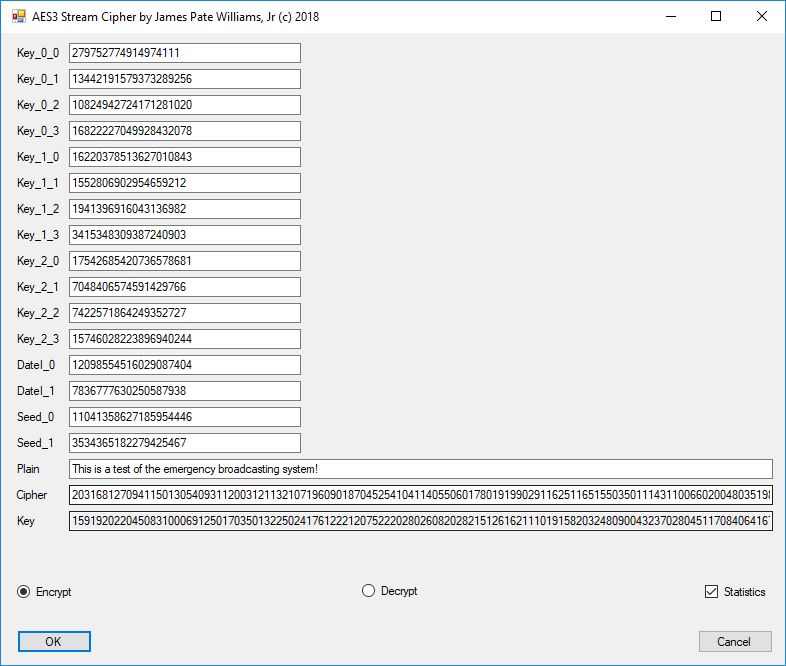
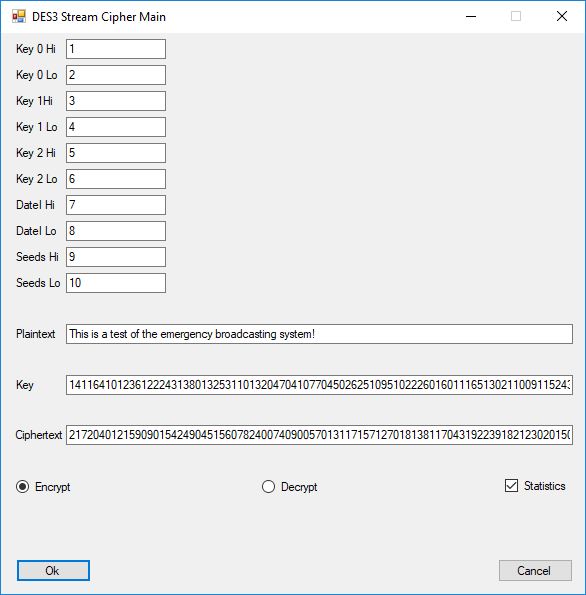
We first encipher the string “This is a test of the emergency broadcasting system!” which is a English language sample of length 52 ASCII characters.

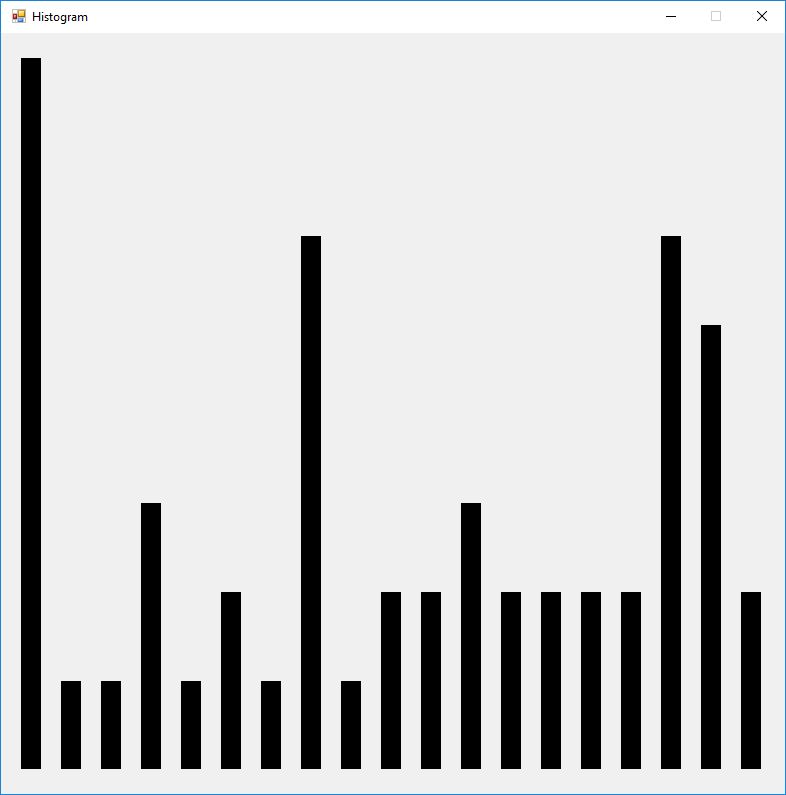
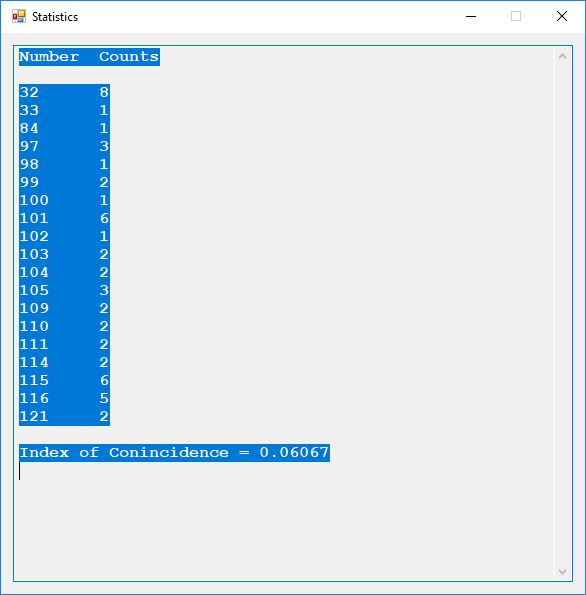
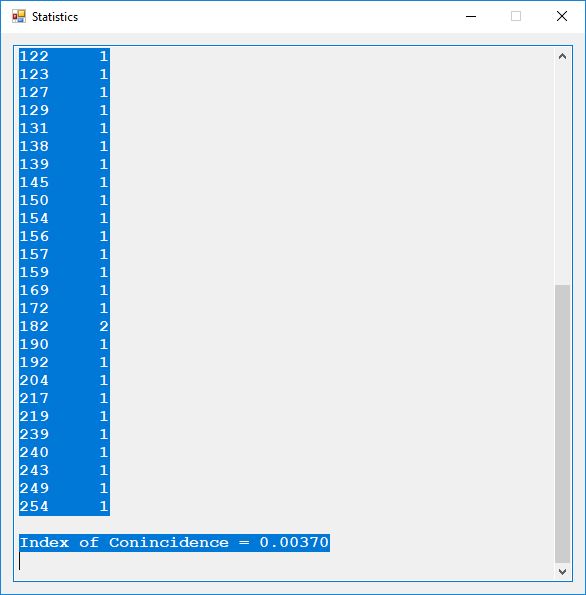
Below is a histogram of the plaintext characters.

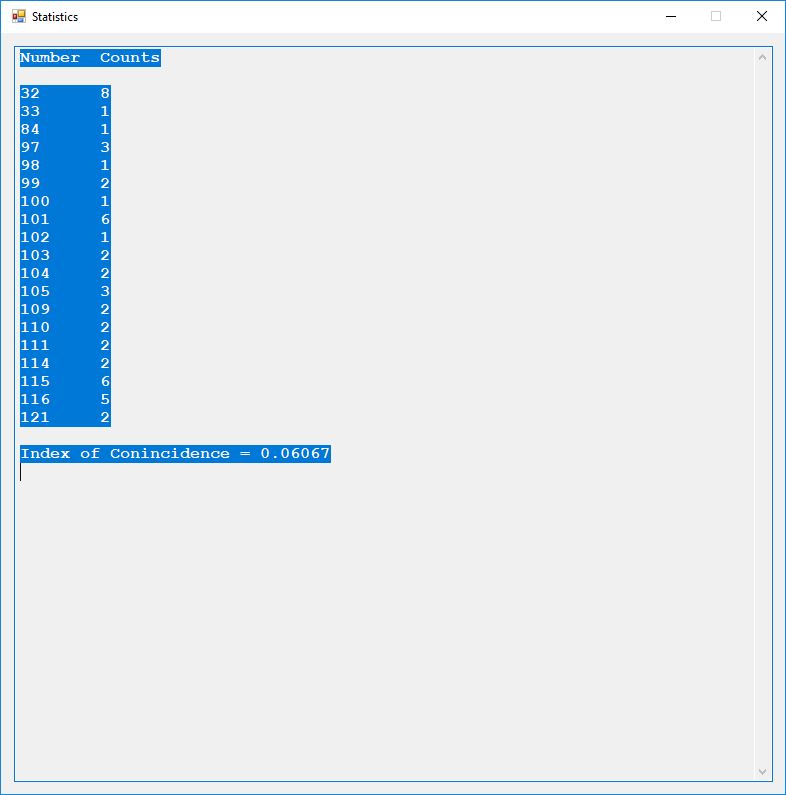
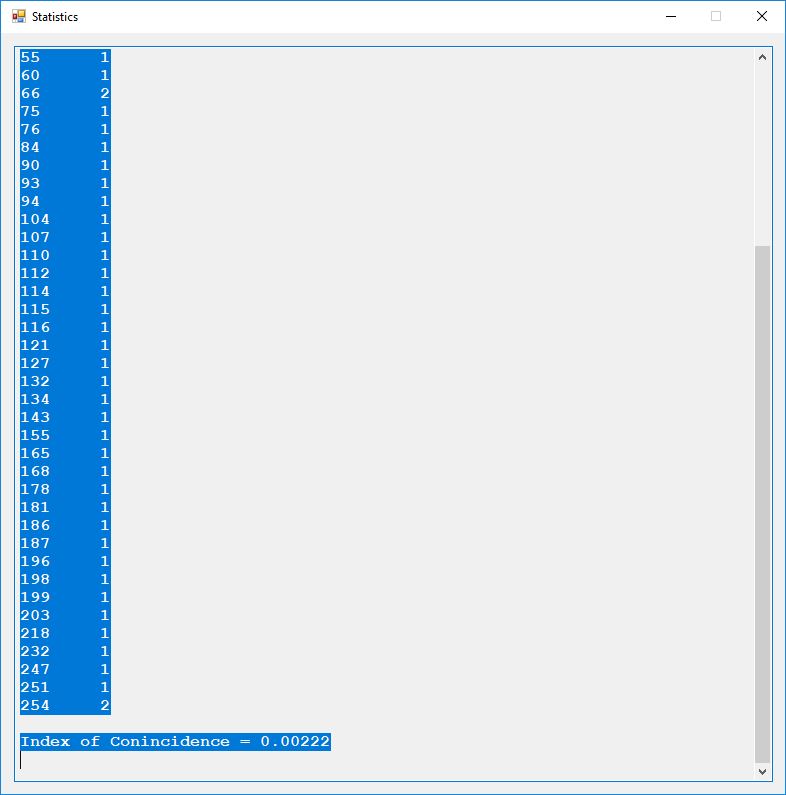
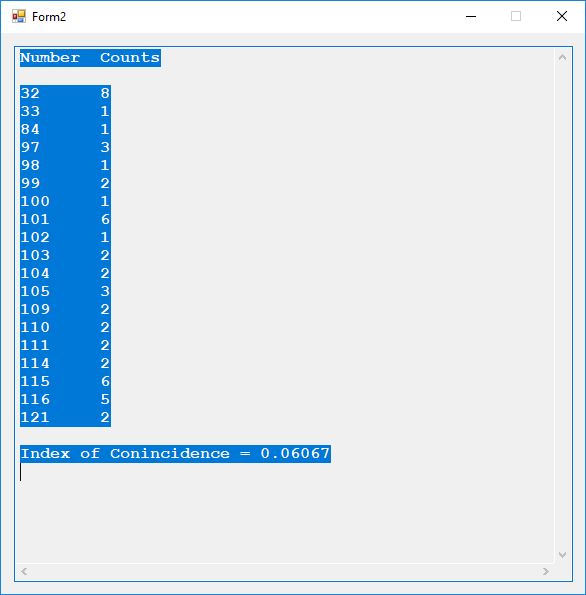
Here are the counts of the different plaintext characters and the statistic known as the index of coincidence. English has an index of coincidence of approximately 0.065, so this short sample is in that ballpark at 0.06067.

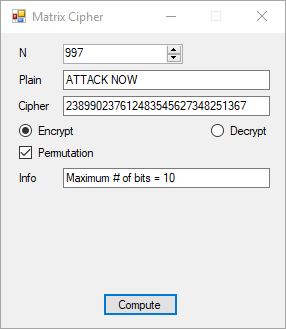
Next we display part of the key material (upper triangular matrix elements), the ASCII encoded plaintext and the last column is the resulting ciphertext.

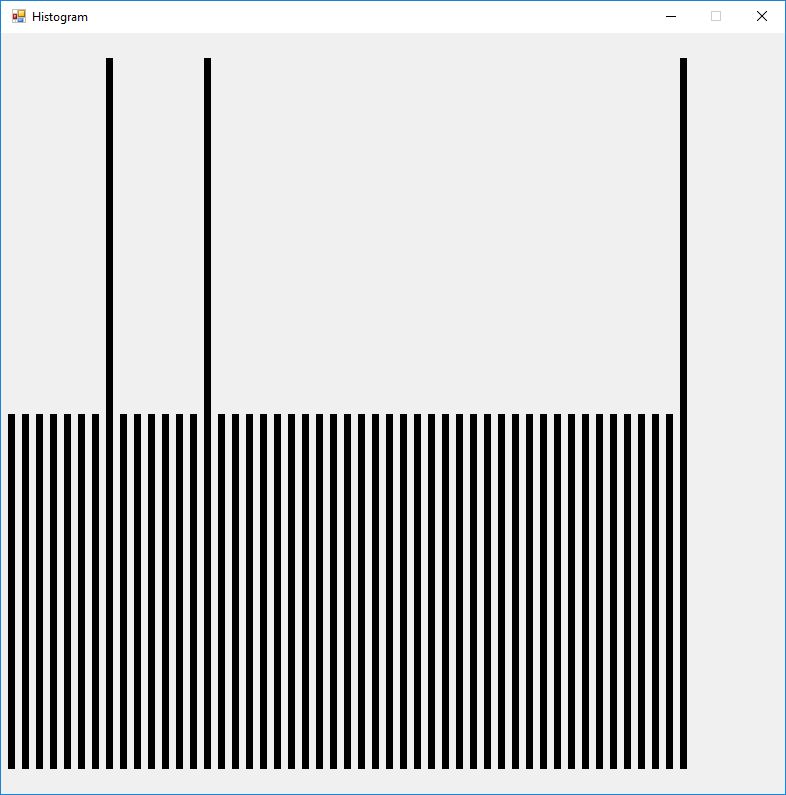
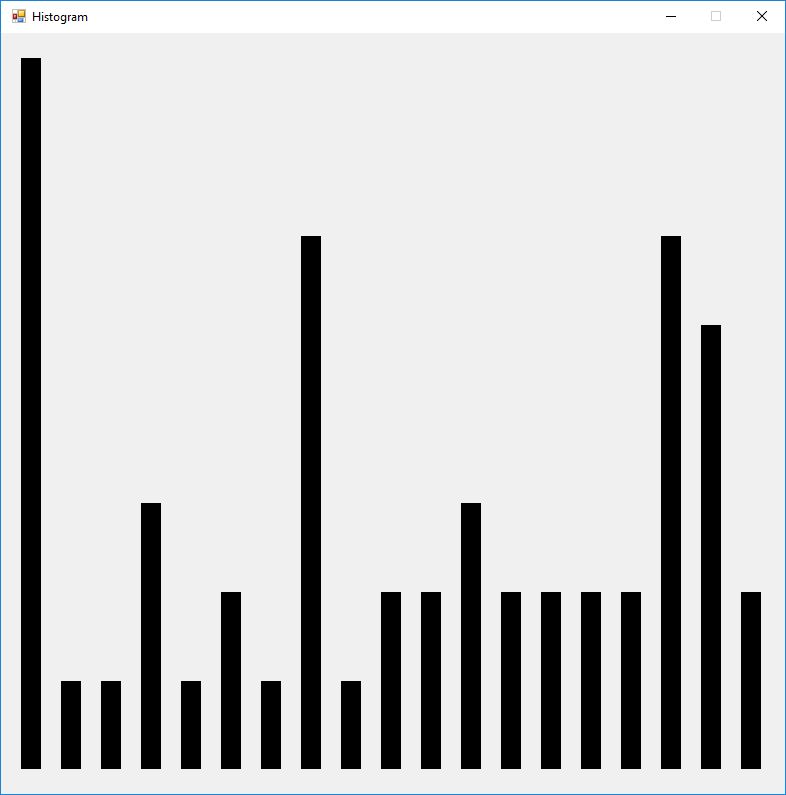
We now display a histogram of the ciphertext.

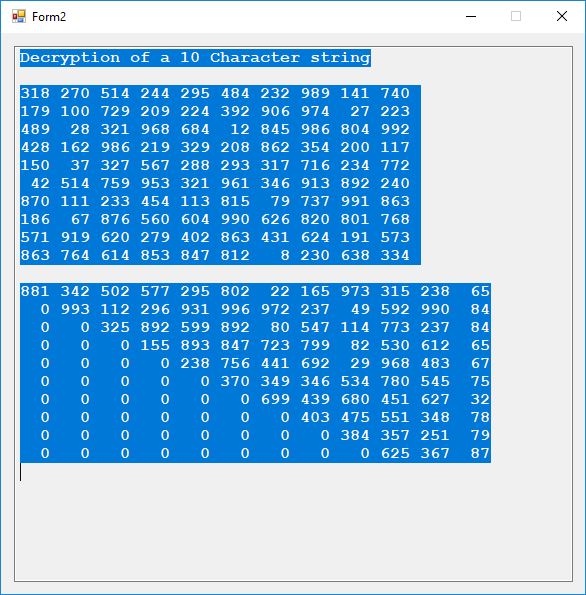
The index of coincidence is 0. Each of the 52 plaintext characters map to a different ciphertext number in the range 2 to 977 inclusive. Now we show the decryption matrix, ciphertext, and plaintext.

We now say a few more words about the cryptanalysis of this matrix cipher. Since the PRNG has a large key space, a direct brute force attack on the PRNG would probably be futile in a milieu without a quantum computer. We can guess values of N and we know that key matrix inverse has n * (n + 1) / 2 elements instead of n * n elements since it is an upper triangular matrix. In our sample the key matrix inverse has 52 * 53 / 2 = 26 * 53 = 1,378 matrix elements. Each matrix element is in the inclusive range 0 to 996 or 997 values. So we would need to brute force test N * n * (n + 1) / 2 possible key matrix inverses. In our case the number is 997 * 1,378 = 1,373,866 which is not a very large number by cryptanalytic standards but how many of those decryptions would make perfectly good sense? A reasonably adept adversary would not reuse the PRNG key and N for a new 52 ASCII character string so each message would require a new  cryptanalytic attack.

Using the upper triangular nature of the key matrix inverse and a further assumption that the plaintext is in the range 32 to 127 or 96 different values, we can reduce the brute force attack to 96 * 1,378 = 132,288 possibilities. Again the adversary could somewhat thwart these cryptanalytic efforts by choosing a much larger N and n.

However, all of this mental masturbation amounts to a mute point since no modern and sane adversary would utilize such an easy cipher to break. Just use a one time pad based on the ANSI X9.17 PRNG utilizing triple-AES instead of triple-DES with three 256-bit E-D-E keys or an astounding 768-bits of key material for the cipher core alone plus 256 bits in additional secret information. The final keyspace of such a scheme would be 1024-bits!