Category: Uncategorized
Diatonic A Minor 360 Beats Per Minute 12 Beats Per Measure 8 Beat Value 256 Measures 4 Minutes and 16 Seconds in Duration
One Synthesizer Four Voices by James Pate Williams Jr
Diatonic E flat 360 beats per minute 12/8 meter signature
Another Randomly Generated Tune by James Pate Williams Jr
A new ditty in Eb diatonic scale at 480 beats per minute 12 / 8 signature.
Some Recordings Using SONAR Platinum by James Pate Williams Jr
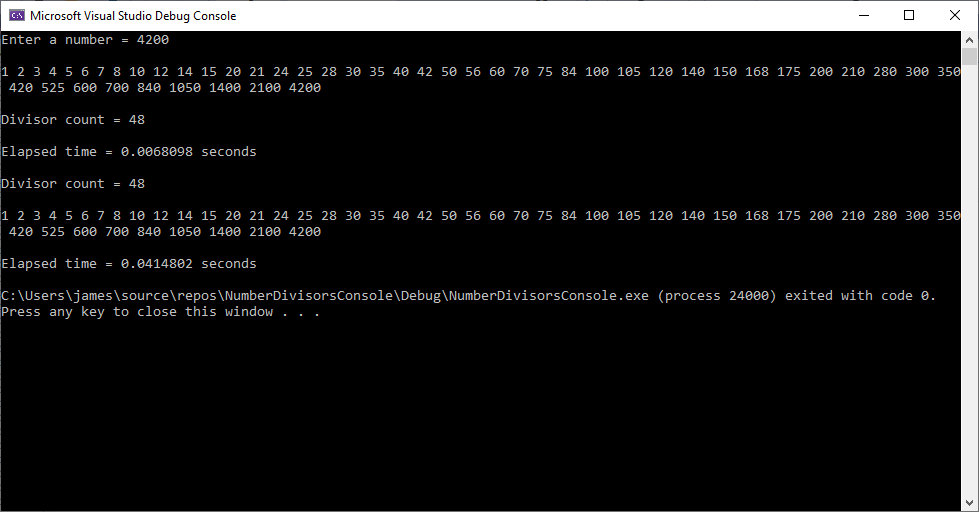
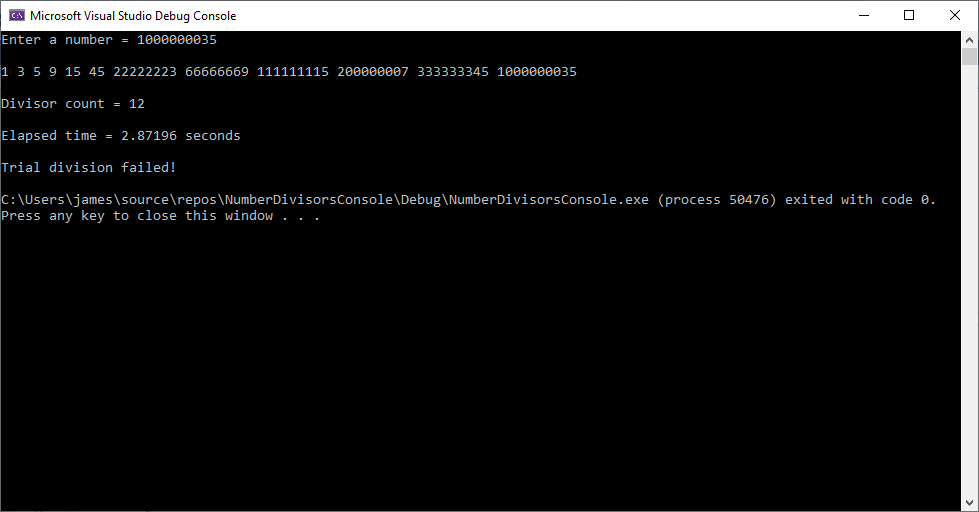
Counting and Enumerating the Number of Divisors of a Natural Number by James Pate Williams, Jr.
A simple number theoretic problem is to count and enumerate the number of divisors of a natural number which is the set { 1, 2, 3, … }. An Order(n) method is to find all numbers between 1 and n such that the number divides n. If you have the prime factorization of n then the number of divisors is the product of the prime factorization (exponents + 1). For example the divisors of 100 are:
1 2 4 5 10 20 25 50 100
The prime factorization of 100 = 2^2 * 5 ^ 2. So the number of divisors is (2 + 1) * (2 + 1) = 9.
Below is a C++ implementation of an algorithm to enumerate and count the number of divisors of a natural number and count the divisors by using the factorization found by trial division.
#include <algorithm>
#include <chrono>
#include <iostream>
#include <vector>
using namespace std;
const int B0 = 10000000;
bool sieve[B0 + 1];
vector<int> prime, divisors, expon, primes, primesSquares;
void Sieve()
{
// Sieve of Eratosthenes
// find all prime numbers
// less than or equal B0
int c = 3, i, inc;
sieve[2] = true;
for (i = 3; i <= B0; i++)
if (i % 2 == 1)
sieve[i] = true;
do
{
i = c * c;
inc = c + c;
while (i <= B0)
{
sieve[i] = false;
i += inc;
}
c += 2;
while (!sieve[c])
c++;
} while (c * c <= B0);
for (i = 2; i <= B0; i++)
{
if (sieve[i])
{
primes.push_back(i);
primesSquares.push_back(i * i);
}
}
}
bool TrialDivision(int number)
{
int bound = B0; // (int)sqrt(number);
for (int i = 0; i < (int)primes.size(); i++)
{
int p = primes[i];
if (p <= bound)
{
if (number % p == 0)
{
int e = 0;
while (number % p == 0)
{
e++;
number /= p;
}
prime.push_back(p);
expon.push_back(e);
}
if (number == 1)
return true;
}
}
return false;
}
void GetDivisors(int n, int count)
{
divisors.push_back(1);
for (int i = 0; i < (int)prime.size(); i++)
{
int p = prime[i];
for (int j = 1; j <= (int)expon[i]; j++)
{
int q = (int)pow(p, j);
divisors.push_back(q);
}
}
bool done = false;
int limit;
do
{
limit = (int)divisors.size();
for (int i = 1; i < limit - 1; i++)
{
int di = divisors[i];
for (int j = i + 1; !done && j < limit; j++)
{
int dj = divisors[j], product = di * dj;
vector<int>::iterator it =
find(divisors.begin(), divisors.end(), product);
if (it == divisors.end())
{
if (divisors.size() < count &&
product <= n && n % product == 0)
divisors.push_back(product);
else if (divisors.size() == count)
done = true;
}
}
}
} while (!done);
std::sort(divisors.begin(), divisors.end());
}
int main()
{
int count = 0, number;
std::cout << "Enter a number = ";
cin >> number;
std::cout << endl;
auto start = chrono::high_resolution_clock::now();
for (int i = 1; i <= number; i++)
{
if (number % i == 0)
{
cout << i << ' ';
count++;
}
}
auto finish = chrono::high_resolution_clock::now();
std::cout << endl << endl;
std::cout << "Divisor count = " << count << endl << endl;
chrono::duration<double> elapsed = finish - start;
std::cout << "Elapsed time = " << elapsed.count()
<< " seconds" << endl << endl;
start = chrono::high_resolution_clock::now();
Sieve();
if (!TrialDivision(number))
{
cout << "Trial division failed!" << endl;
return 0;
}
count = 1;
for (int i = 0; i < (int)expon.size(); i++)
count *= expon[i] + 1;
finish = chrono::high_resolution_clock::now();
std::cout << "Divisor count = " << count << endl << endl;
GetDivisors(number, count);
for (int i = 0; i < (int)divisors.size(); i++)
std::cout << divisors[i] << " ";
std::cout << endl << endl;
elapsed = finish - start;
std::cout << "Elapsed time = " << elapsed.count()
<< " seconds" << endl;
}

On Jigsaw Puzzle Solving and Computer Chess by James Pate Williams, Jr.
I have been playing a jigsaw puzzle app on my Microsoft desktop. The name of the app is “Jigsaw Puzzle HD”. I get one free puzzle per day. I set the number of pieces to 49 which is a 7 by 7 square. It takes me approximately 10 to 20 minutes to solve puzzle. The pieces are large on my Dell display but there is not room to spare using a maximized window and 49 pieces.
Here are some tips I have learned about jigsaw puzzle solving (an algorithm):
- Roughly separate the pieces by color
- Separate the four boundaries out from the sorted pieces
- Construct the four boundaries of the puzzle
- Use a sharper color sort to really untangle the middle pieces
- Solve small areas of the middle of the puzzle
- Iterate the preceding steps until the solution is found
I have a nice chess playing app on my desktop computer named “The Chess Lv. 100”. This chess game has 100 levels and Level 1’s Rating is 258 and Level 100’s Rating is 2300. I have a Level 12 Rating of 849 which is probably lower than my United States Chess Federation Rating back in the era 1968 to 1971. I play Level 8 to 12 computer opponents and sometimes venture as high as Level 25 which has a rating of 1094. Here is some information about the United States Chess Federation ratings:
I do not have a simple algorithm for chess, but do not make blunders and try to look several moves into future before you move. Also a good working knowledge of openings, middle-games, and end-games helps.
Battleship Iowa (BB-61) Exterior Ballistics Revisited by James Pate Williams Jr
I modified my battleship Iowa application to use the following input data based on the textbook “Exterior ballistics, 1935” by Ernest Edward Herrmann of the United States Naval Academy:




We get the following data from the Ordnance Pamphlet 770 October 1941
https://eugeneleeslover.com/USN-GUNS-AND-RANGE-TABLES/OP-770-1.html

Charge of the Golden Chariots by James Pate Williams, Jr.
Ramses and his golden chariots chasing Moses and the rest of the fleeing Jews to the Red Sea (Genesis and Exodus, King James Version).
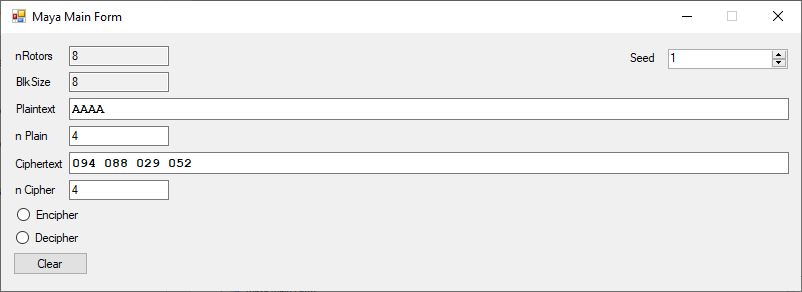
Maya Cipher System by James Pate Williams, Jr.
Number of External Keys = 2 ^ 31 – 1 = 2,147,483,647 Possibilities
Number of the Internal Keys = n-Rotors (8) * 128 (# of standard ASCII characters) = 1024 Internal Keys
Beaufort Internal Cipher with 8 alphabets of 128 internal keys
The system is weak in its current configuration
Here is the 4 A, 8 A, and 12 A cases

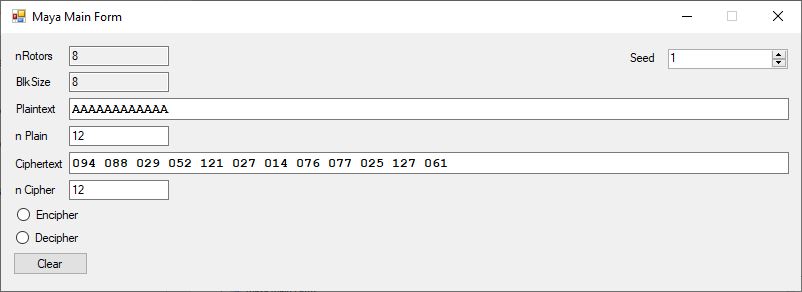
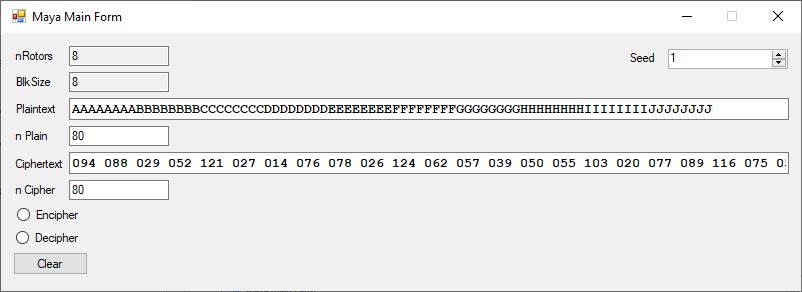
I need to strengthen the external key length to at least 2^192 key possibilities by adding a cryptographic secure random number generator instead of a standard weak C type pseudorandom number generator. Another way of strengthening the system would be to rotate each rotor after a one character or one block use. The block length is 8 ASCII characters.