Stream Cipher – Numerical Explorations

Five Stream Ciphers Created from Five Pseudorandom Number Generators Built Using the Tests of FIPS 140-1 by James Pate Williams, BA, BS, MSwE, PhD

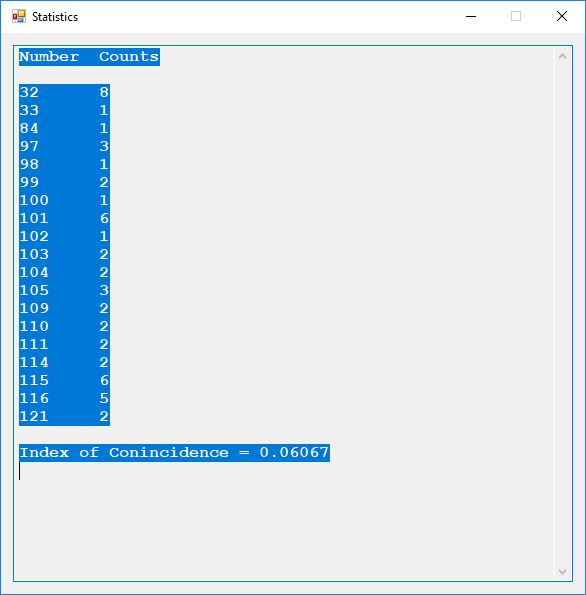
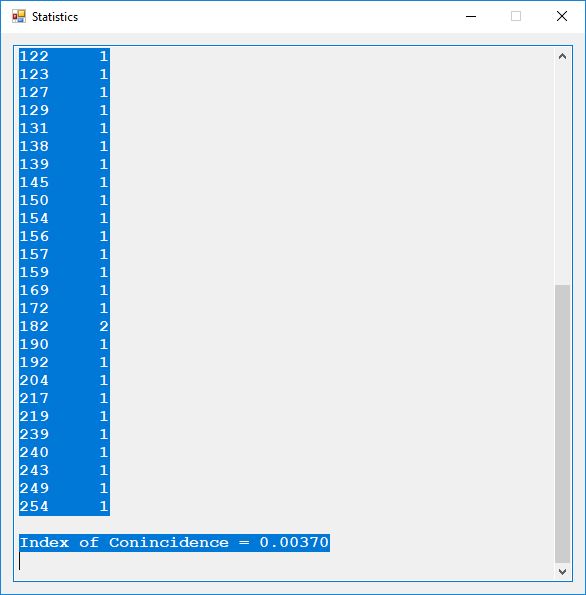
The five pseudorandom number generators are:

Triple-AES based ANSI X9.17 PRNG
Triple-DES based ANSI x9.17 PRNG
RSA based PRNG
Micali-Schnorr PRNG
Blum-Blum-Shub PRNG

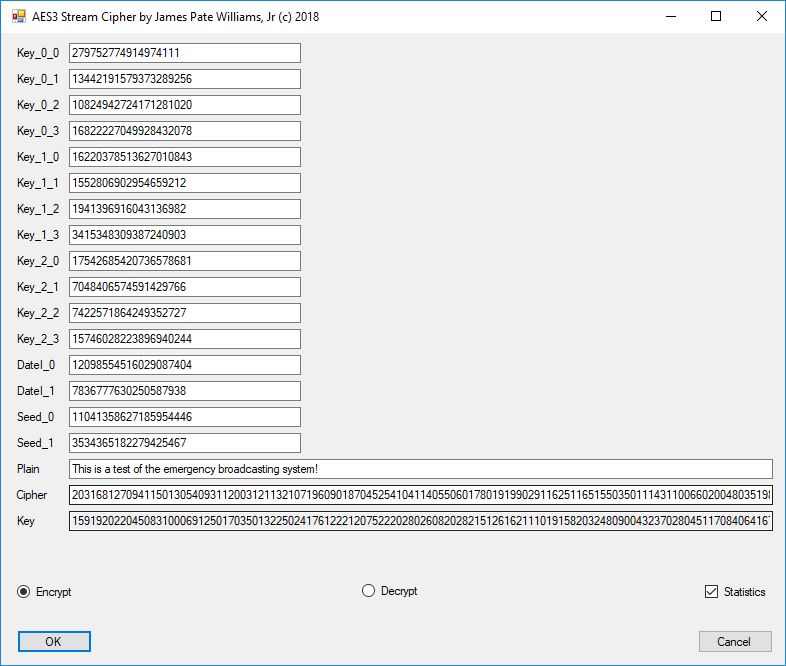
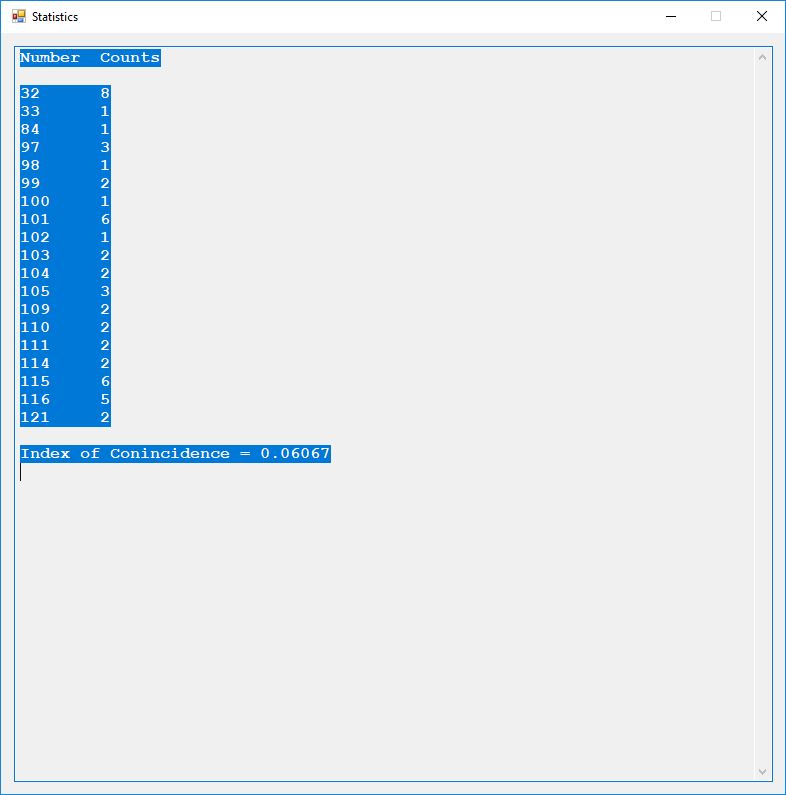
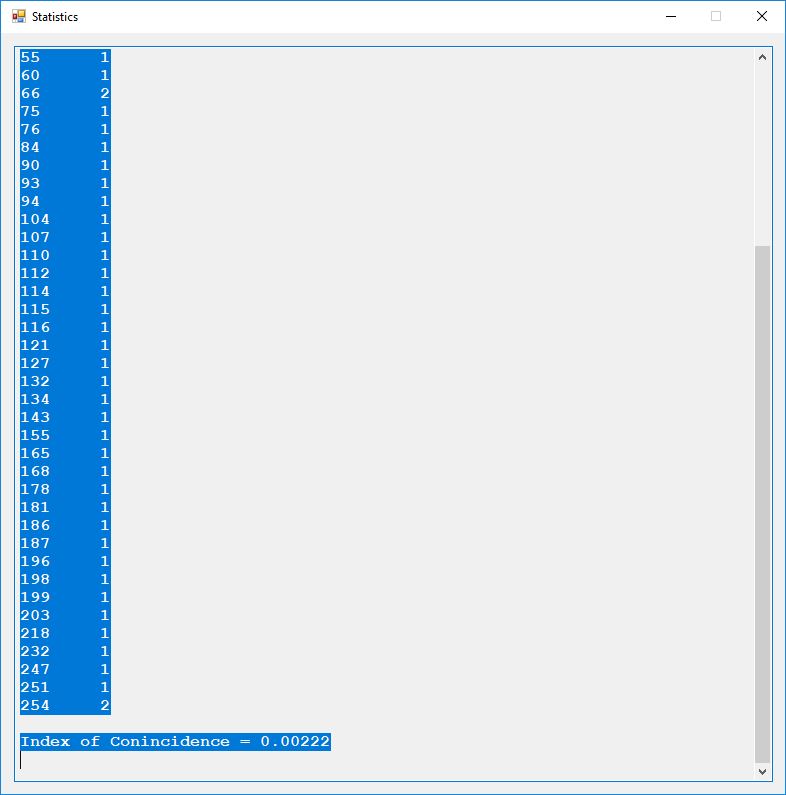
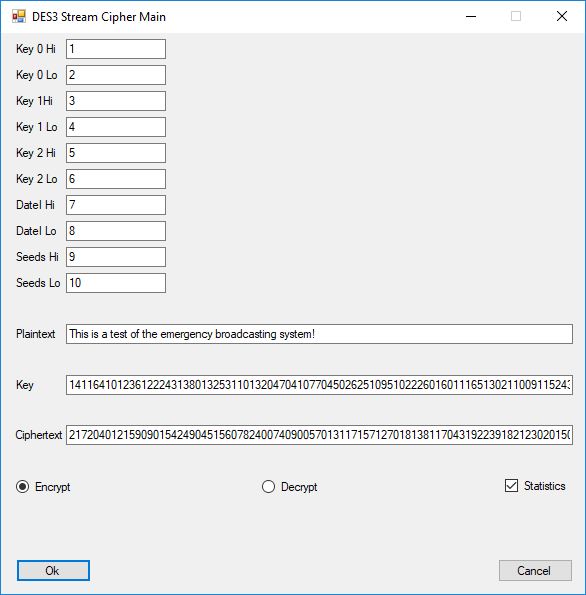
Five stream ciphers were created using 1 to 5. Screenshots of the C# application follow:

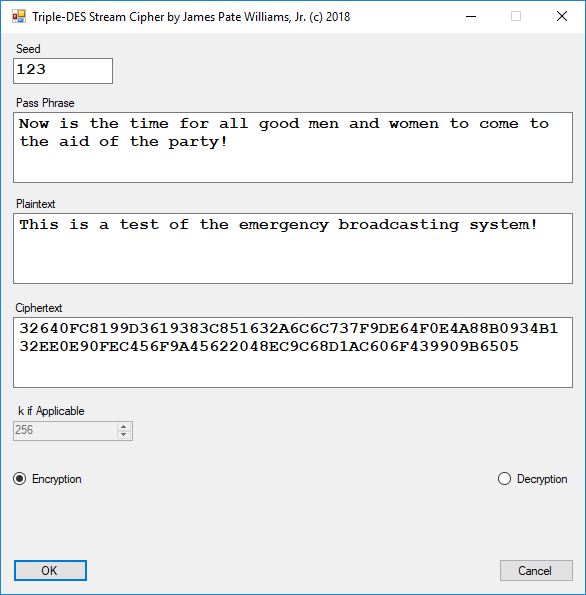
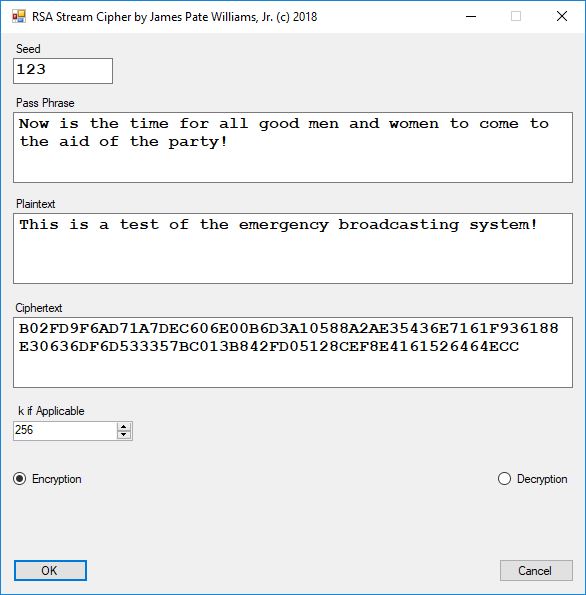
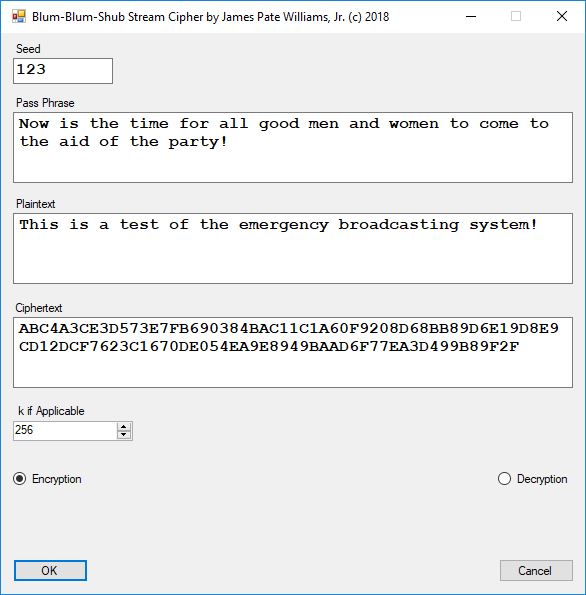
sc aes sc des sc rsa sc ms sc bbs

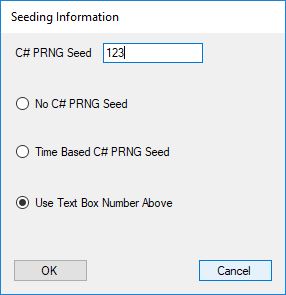
The pass phrase optimally should consist of 147 ASCII characters. If the number of pass phrase ASCII characters is less than 147 then more random ASCII characters are added using the standard C# pseudorandom number generator seeded with the parameter named Seed. The user defined parameter k is used by RSA, Micali-Schnorr, and Blum-Blum-Shub pseudorandom number generators. It is the approximate bit length of the large composite number composed of two large probable prime numbers. The real key lengths of all the stream ciphers is about 1024-bits for 1, 3, 4, and 5 and 296-bits for 2. I’d strongly suggest using 1 and/or 5.

Triple-AES Stream Cipher Using the ANSI X9.17 Pseudorandom Number Generator (PRNG) by James Pate Williams, Jr. BA, BS, MSwE, PhD

The Advanced Encryption Standard (AES) is fully described in the National Institute of Standards and Technology (NIST) publication:

Click to access NIST.FIPS.197.pdf

AES is a secret key block cipher with a block length of 128-bits and variable key lengths of 128-bits, 192-bits, and 256-bits.

The ANSI X9.17 pseudorandom number generator is described by Alfred J. Menezes, ET AL. in the Handbook of Applied Cryptography on page 176 5.11 Algorithm.

We use triple-AES with three 256-bit keys in Encryption-Decryption-Encryption mode. Also we utilize two 128-bit numbers. The total key space is (768 + 256)-bits = 1024-bits.

We now illustrate in the following screenshots our C# implementation of a stream cipher using the preceding algorithms.

We use the following dialog to allow under certain circumstances the application to randomly generate the seed material for our PRNG. Unfortunately, the built-in C# PRNG only has 2^31 -1 = 2147483647 different seeds. This cuts down on the amount of thought and typing required but is inherently dangerous due to the relatively small number of seeds. If you want true security the requisite sixteen 64-bit numbers must be random.

AES3 Stream Cipher 0

AES3 Stream Cipher 1

AES3 Stream Cipher Encrypt 0

AES3 Stream Cipher Encrypt 1

AES3 Stream Cipher Decrypt 0

AES3 Stream Cipher Decrypt 1

Optimally we would like to 0 index of coincidence, but 0.00222 is reasonably acceptable.

ANSIX9_17 Source Code

Triple-DES Stream Cipher Using the ANSI X9.17 Pseudorandom Number Generator (PRNG) by James Pate Williams, Jr. BA, BS, MSwE, PhD

In this blog post we give some information about my implementation of a C# triple-DES stream cipher using the ANSI X9.17 pseudorandom number generator of 5.11 Algorithm in the Handbook of Applied Cryptography by Alfred J. Menezes, ET AL. page 173. This is about as close as I can come to a one time pad (perfect security) utilizing a triple-DES based function for key generation. I suspect the security is pretty tight as long as one does not stupidly reuse a key. Recall from my previous blogs on the ANSI X9.17 matrix cipher that key space is 168-bits for triple-DES in E-D-E mode and an additional 128-bits in other key parameters for a total of 296-bits.

DES3 SC Encrypt