Category: C# Computer Programming Language
Live Person-to-Person Tutoring
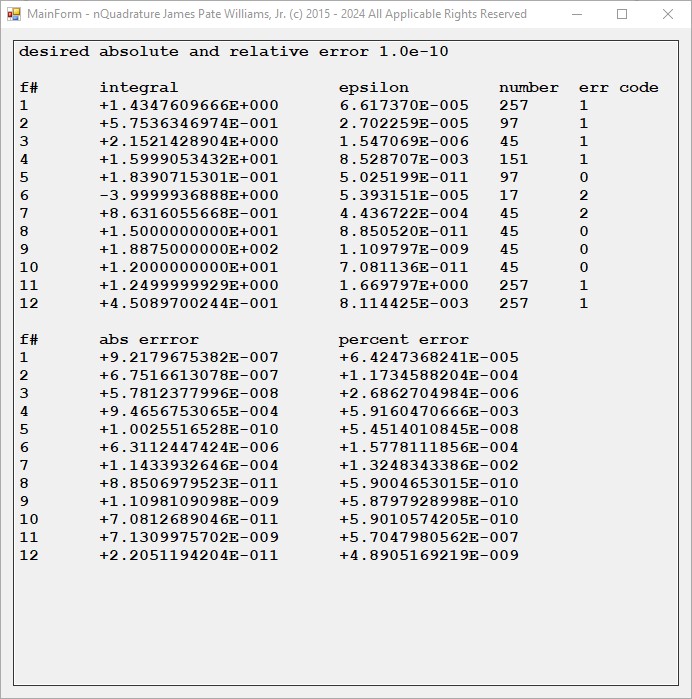
Blog Entry © Saturday, October 5, 2024, by James Pate Williams, Jr. Multidimensional Integrals
Blog Entry © Thursday, October 3, 2024, by James Pate Williams, Jr. A Mixture of Numerical Analysis and General Relativity Physics
Blog Entry (c) Wednesday, October 2, 2024, by James Pate Williams, Jr. First Order Coupled Ordinary Differential Equations
Blog Entry (c) Monday September 16, 2024, by James Pate Williams, Jr. Variation of the Gravitational Acceleration on Earth with Height
Blog Entry (c) Saturday, September 14, 2024, The Mandelbrot Set by James Pate Williams, Jr. A Simple Fractal Self-Similar Curve

Blog Entry (c) Friday, September 13, 2024, by James Pate Williams, Jr.
Blog Entry (c) Thursday, September 12, 2024, by James Pate Williams, Jr. Some Backpropagation Neural Network Results
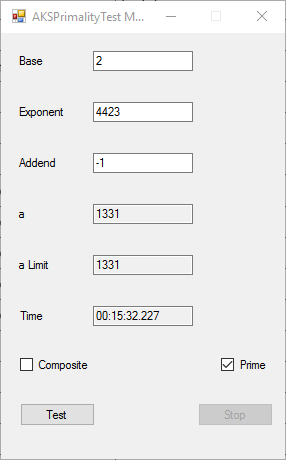
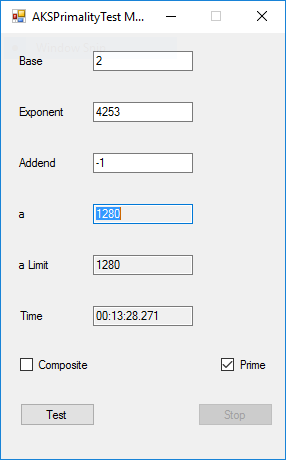
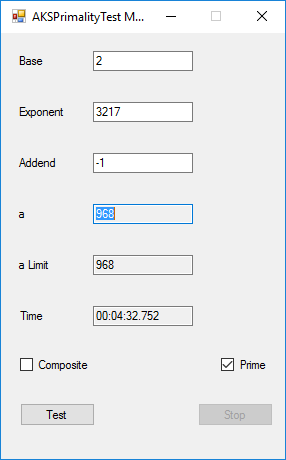
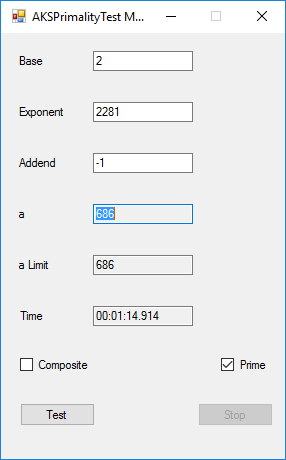
BigInteger Multitasking Agrawal, Kayal, and Saxena (AKS) Primality Test (c) June 19, 2016, by James Pate Williams, Jr. Microsoft TechNet Project Description
This application implements the algorithm described in the paper at the URL http://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf. I replaced Step 1 of the algorithm with the Miller-Rabin probabilistic primality test. If that test shows that the number is composite, I return the value COMPOSITE. This algorithm is much easier to implement and understand that Wieb Bosmer’s Primality Proving with Cyclotomy also known as the Jacobi sums primality test. As a test we determine that the following Mersenne numbers are prime: M_1279, M_2203, M_2281, M_3217, and M_4253 where M_n = 2 ^ n – 1, and the primes have 386, 664, 687, 969, and 1281 decimal digits, respectively. M_1279 was first proven prime by Raphael M. Robinson on June 25, 1952, using the Lucas-Lehmer test on a SWAC computer. The same author found that M_2203 was prime on October 7, 1952, and M_2281 was prime on October 9, 1952, using the same method and computer. Hans Riesel determined that M_3217 was prime on September 8, 1957, using the Lucas-Lehmer test on a BESK computer. M_4253 was proven prime on November 3, 1961 by Alexander Hurwitz using the Lucas-Lehmer test on an IBM 7090 mainframe computer. See http://www.mersenne.org/primes/ for many more Mersenne primes. All of the computations illustrated below were performed on a late November 2015 Dell XPS 8900 computer with 16 GB RAM Intel(R) Core(TM) i7-6700K CPU @ 4.00 GHz running Windows 10 Pro. The .Net framework is .Net 4.5.2. This is a multitasking version of the original BigInteger variant of the application. Someone with a quad core CPU with 8 virtual processors can try NumberTasks = 8 to see if that speeds up this application more or less. I usually try to limit the number of tasks to actual number of cores.