Handbook of Applied Cryptography – Page 3

Chapter 9 of the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone Highlights Unkeyed Hash Functions by James Pate Williams, Jr. BA, BS, MSwE, PhD

In this first installment of Chapter 9 Hash Functions and Data Integrity of the Handbook, we concentrate on the unkeyed hash functions mentioned in the Chapter which are:

Matyas-Meyer-Oseas Hash 9.41 Algorithm page 341
Davies-Meyer Hash 9.42 Algorithm page 341
Miyaguchi-Preneel Hash 9.43 Algorithm page 341
MDC-2 (DES Based) 9.46 Algorithm page 342
MDC-4 (DES Based) 9.47 Algorithm page 343
MD4 9.49 Algorithm page 346
MD5 9.51 Algorithm page 347
SHA-1 (Secure Hash Algorithm 1) 9.53 Algorithm page 348-349
RIPMD-160 9.55 Algorithm pages 350-351

The first five algorithms are based on the IBM-NIST-NSA encryption algorithm DES (Data Encryption Standard).

Chapter 9 Unkeyed 1

Matyas-Meyer-Oseas DES Hash Function
abcdefghijklmnopqrstuvwxyz
IV = 01ad27b0 75851f2a
H1 = 62af6ffa e32867a0
Zbcdefghijklmnopqrstuvwxyz
IV = 01ad27b0 75851f2a
I1 = 567f7eaf 7420eb6f
number of changed bits by a five bits input change = 27

Davies-Meyer DES Hash Function
abcdefghijklmnopqrstuvwxyz
IV = 464f95ff 30d042d1
H1 = be1c30f4 2f6fc905
Zbcdefghijklmnopqrstuvwxyz
IV = 464f95ff 30d042d1
I1 = e56ec4b7 ffd98172
number of changed bits by a five bits input change = 33

Miyaguchi-Preneel DES Hash Function
abcdefghijklmnopqrstuvwxyz
IV = 164502df 2264bd00
H1 = d866343a 137eee2a
Zbcdefghijklmnopqrstuvwxyz
IV = 164502df 2264bd00
I1 = becbad0e 0ca8fa64
number of changed bits by a five bits input change = 32

Chapter 9 Unkeyed 2

MDC_2 DES Hash Function
abcdefghijklmnopqrstuvwxyz
G0 = a2a9a035 554856b1
G0T = ed24d012 d536f455
Zbcdefghijklmnopqrstuvwxyz
H0 = 5a79b365 970b3216
H0T = 2694dd17 0d93ddb1
number of changed bits by a five bits input change = 55

MDC-4 DES Hash Function
abcdefghijklmnopqrstuvwxyz
IV = 3cd408f2 528789b6
IVT = 0ac7b125 5a8a8729
G0 = 80140bb0 e49cc013
G0T = 80140bb0 e49cc013
Zbcdefghijklmnopqrstuvwxyz
IV = 3cd408f2 528789b6
IVT = 0ac7b125 5a8a8729
H0 = 37d40179 ce50bcc9
H0T = 37d40179 ce50bcc9
number of changed bits by a five bits input change = 62

Chapter 9 MD4

MD4

0x31d6cfe0 
0xd16ae931 
0xb73c59d7 
0xe0c089c0

a
0xbde52cb3 
0x1de33e46 
0x245e05fb 
0xdbd6fb24

abc
0xa448017a 
0xaf21d852 
0x5fc10ae8 
0x7aa6729d

abcdefghijklmnopqrstuvwxyz
0xd79e1c30 
0x8aa5bbcd 
0xeea8ed63 
0xdf412da9

Chapter 9 MD5

MD5

0xd41d8cd9 
0x8f00b204 
0xe9800998 
0xecf8427e

a
0x0cc175b9 
0xc0f1b6a8 
0x31c399e2 
0x69772661

abc
0x90015098 
0x3cd24fb0 
0xd6963f7d 
0x28e17f72

abcdefghijklmnopqrstuvwxyz
0xc3fcd3d7 
0x6192e400 
0x7dfb496c 
0xca67e13b

Chapter 9 SHA

SHA-1

0xda39a3ee 
0x5e6b4b0d 
0x3255bfef 
0x95601890 
0xafd80709

a
0x86f7e437 
0xfaa5a7fc 
0xe15d1ddc 
0xb9eaeaea 
0x377667b8

abc
0xa9993e36 
0x4706816a 
0xba3e2571 
0x7850c26c 
0x9cd0d89d

abcdefghijklmnopqrstuvwxyz
0x32d10c7b 
0x8cf96570 
0xca04ce37 
0xf2a19d84 
0x240d3a89

Chapter 9 RIPEMD

RIPEMD-160

0x9c1185a5 
0xc5e9fc54 
0x61280897 
0x7ee8f548 
0xb2258d31

a
0x0bdc9d2d 
0x256b3ee9 
0xdaae347b 
0xe6f4dc83 
0x5a467ffe

abc
0x8eb208f7 
0xe05d987a 
0x9b044a8e 
0x98c6b087 
0xf15a0bfc

abcdefghijklmnopqrstuvwxyz
0xf71c2710 
0x9c692c1b 
0x56bbdceb 
0x5b9d2865 
0xb3708dbc

Test vectors for MD4, MD5, SHA-1, and RIPEMD-160 can be found in Table 9.6 of the Handbook on page 345.

Chapter 8 of the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone Highlights by James Pate Williams, Jr. BA, BS, MSwE, PhD

Chapter 8 of the Handbook is devoted to the public key encryption systems available in the late 1990s. The most interesting algorithms in my humble opinion are:

RSA (Rivest, Shamir, and Adleman) Public Key Algorithm
Rabin Public Key Encryption Public Key Algorithm
Generalized ElGamal Public Key Encryption Algorithm

My original C implementations that were created in the period 1996 to 1998 utilized the Free LIP (Free Large Integer Package) which was designed and implemented by Arjen K. Lenstra. Later, this particular Professor Lenstra helped in the development of the General and Special Number Field Sieve. He is also of factoring large integers fame. I used the C# language again in my testing implementations.

First we display the RSA results using an artificially small bit size of 256 bits.

RSA Chapter 8

Key Generation

k :
256
n :
 71748965933911640426880165731135238544415795986802264097926042451628661227723
d :
17534201656439215903029293361854099060868747295577796745436087467699018441853
e :
46435195294099703737718314333558788184905780513774200544498948302189056810037

Encryption

plaintext :
Now is the time for all good men to come to the aid of the party
4e 6f 77 20 69 73 20 74 68 65 20 74 69 6d 65 20 66 6f 72 20 61 6c 6c 20 67 6f 6f 64 20 6d 65 6e 20 74 6f 20 63 6f 6d 65 20 74 6f 20 74 68 65 20 61 69 64 20 6f 66 20 74 68 65 20 70 61 72 74 79

bytes per block = 32
number blocks = 3

plaintext :
Now is the time for all good men to come to the aid of the party

ciphertext :
37 97 74 00 91 d6 09 6e f6 92 c0 7d 2b 55 27 3f 49 4c 8f 56 a0 3a 2e fb 24 9d cc a7 f4 6e c5 88 a3 5b 1c 5c 9e d3 c8 2e dd 4e f0 1a 4c 13 03 ec 88 ea 84 19 56 bc 8e b1 00 04 1f 16 cf 26 16 0a 68 75 69 03 21 fe 9f bd f0 0b 41 9b 6d 42 0f bc 3a c2 cc 81 08 5f 88 8c 55 f3 ac 63 03 00 73 23

Decryption

4e 6f 77 20 69 73 20 74 68 65 20 74 69 6d 65 20 66 6f 72 20 61 6c 6c 20 67 6f 6f 64 20 6d 65 6e 20 74 6f 20 63 6f 6d 65 20 74 6f 20 74 68 65 20 61 69 64 20 6f 66 20 74 68 65 20 70 61 72 74 79

plaintext :
Now is the time for all good men to come to the aid of the party

Rabin Chapter 8

Next we illustrate the Rabin public key cryptosystem using a 12-bit key.

Key Generation

k = 128
n = 211556863392599022339215233849307913121
p = 13935902955925754761
q = 15180707275422140761

Encryption

plaintext = Now is the time for all good men to come to the aid of the party
4e 6f 77 20 69 73 20 74 68 65 20 74 69 6d 65 20 66 6f 72 20 61 6c 6c 20 67 6f 6f 64 20 6d 65 6e 20 74 6f 20 63 6f 6d 65 20 74 6f 20 74 68 65 20 61 69 64 20 6f 66 20 74 68 65 20 70 61 72 74 79 
bytes per block = 16
number blocks = 5
a7 f3 64 45 7e 4d 63 7a fc 6f f4 58 05 2a 00 13 4c ea 0f 35 f2 a9 06 a0 18 84 7f f8 e0 1a ab 29 dd f7 77 7d a3 e0 5e fa 38 91 b3 43 f0 3b 45 38 20 82 df 81 56 28 eb fc d6 fd 1a 02 4b c4 6f 6b 00 40

Decryption

plaintext = Now is the time for all good men to come to the aid of the party

Now we move onto the generalized ElGamal public key cryptosystem.

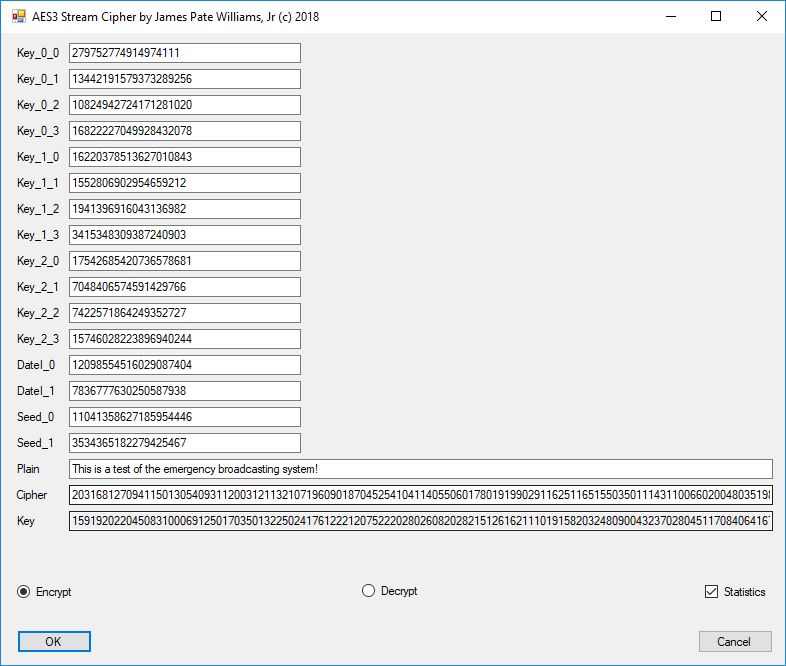
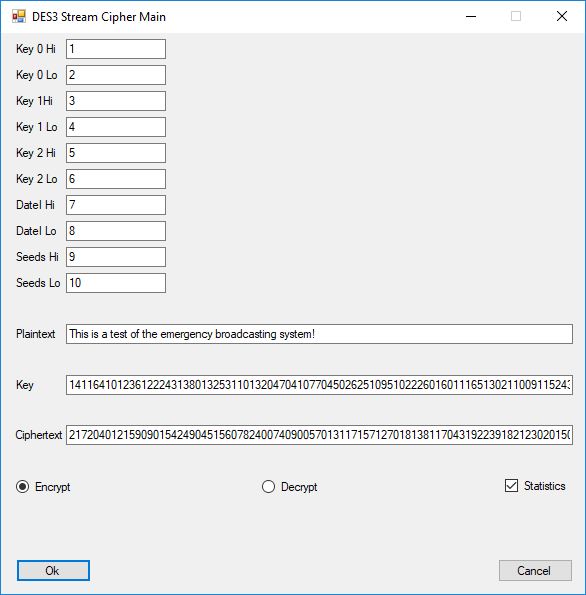
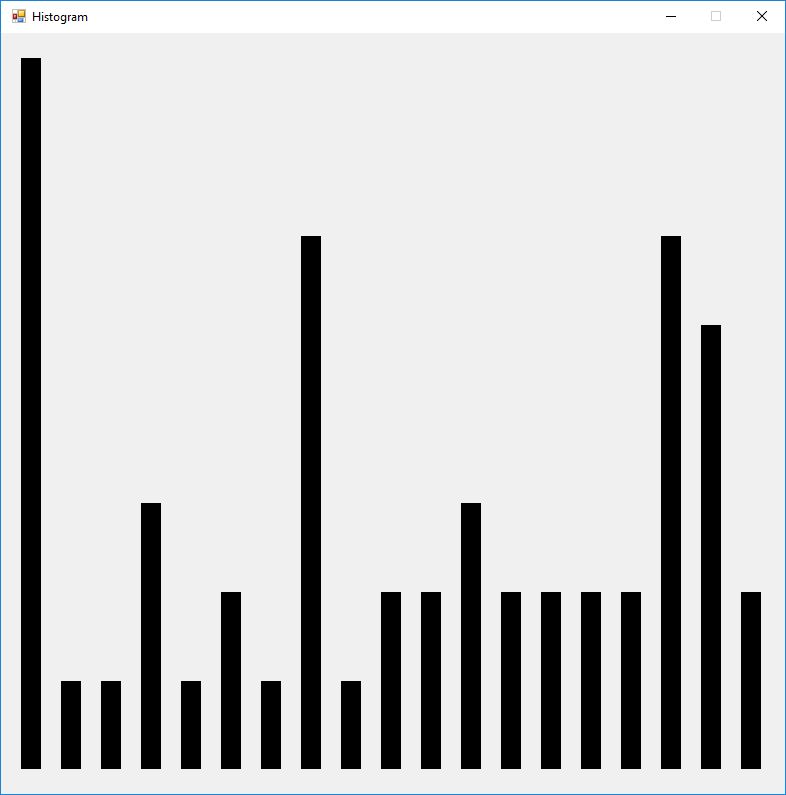
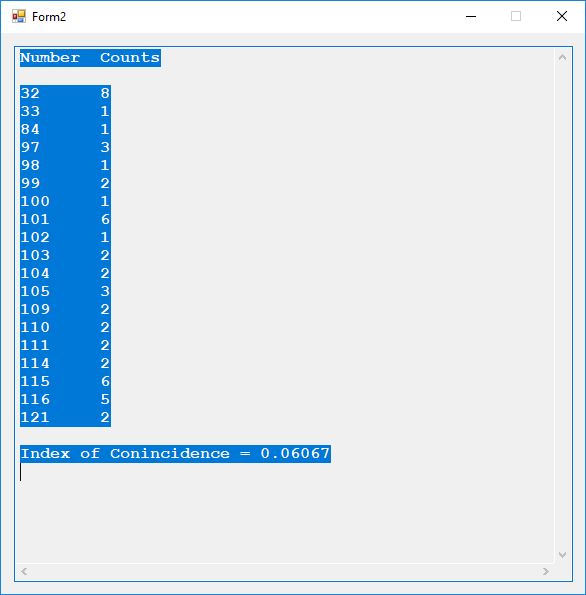
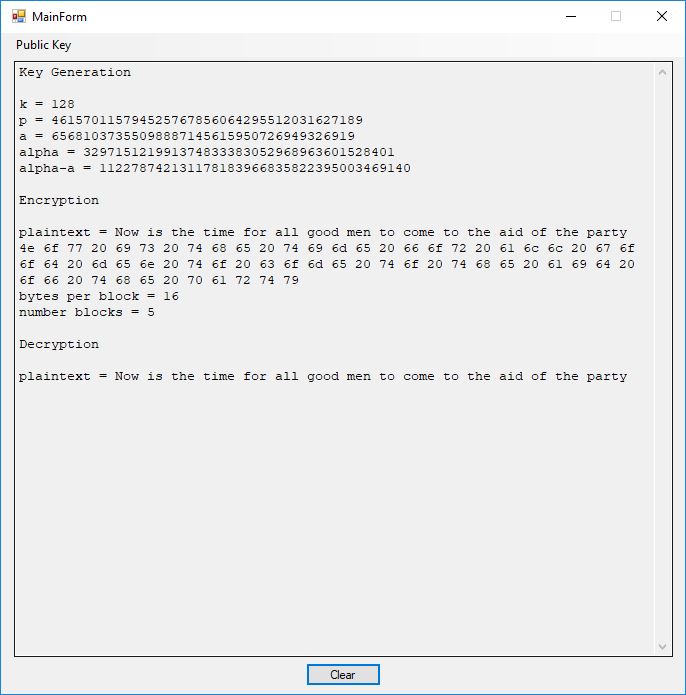
ElGamal Chapter 8

Key Generation

k = 128
p = 461570115794525767856064295512031627189
a = 65681037355098887145615950726949326919
alpha = 329715121991374833383052968963601528401
alpha-a = 112278742131178183966835822395003469140

Encryption

plaintext = Now is the time for all good men to come to the aid of the party
4e 6f 77 20 69 73 20 74 68 65 20 74 69 6d 65 20 66 6f 72 20 61 6c 6c 20 67 6f 6f 64 20 6d 65 6e 20 74 6f 20 63 6f 6d 65 20 74 6f 20 74 68 65 20 61 69 64 20 6f 66 20 74 68 65 20 70 61 72 74 79 
bytes per block = 16
number blocks = 5

Decryption

plaintext = Now is the time for all good men to come to the aid of the party

Chapter 7 of the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone Highlights by James Pate Williams, Jr. BA, BS, MSwE, PhD

From a software engineer and computer scientist’s point of view, the key sections on block ciphers in this chapter of the Handbook are 7.4 DES, 7.5 FEAL, 7.6 IDEA, and 7.7 SAFER, RC5, … My original C implementations are probably from the era 1996 to 1998 of my life. In January and February of 2017 I translated the C code to C#. The results below are from the test application. I added some code on the triple-DES algorithm.

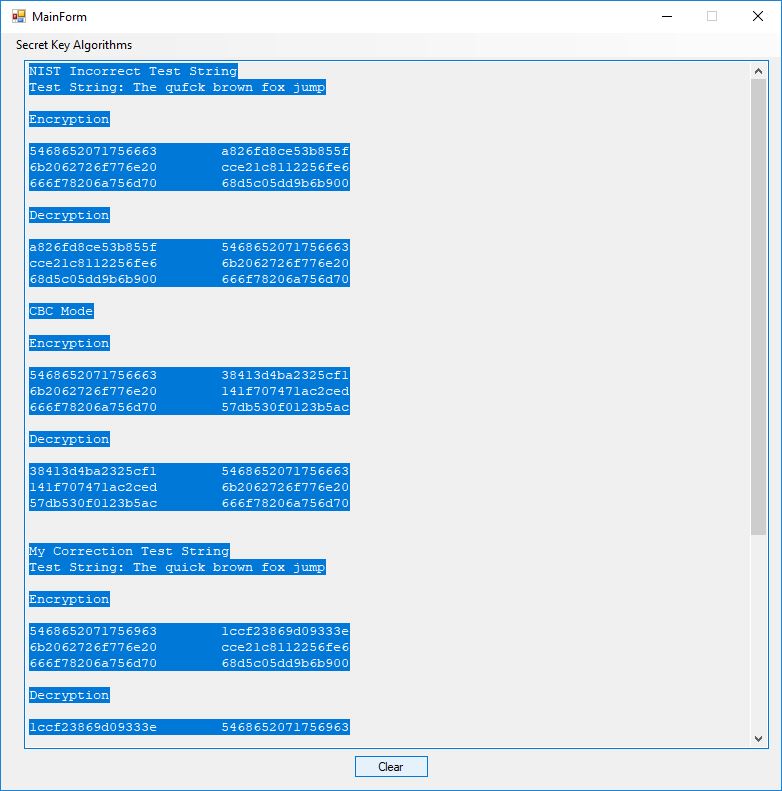
DES3 Chapter 7

Here are the numbers from the triple DES test.

NIST Incorrect Test String
Test String: The qufck brown fox jump

Encryption

5468652071756663 a826fd8ce53b855f
6b2062726f776e20 cce21c8112256fe6
666f78206a756d70 68d5c05dd9b6b900

Decryption

a826fd8ce53b855f 5468652071756663
cce21c8112256fe6 6b2062726f776e20
68d5c05dd9b6b900 666f78206a756d70

CBC Mode

Encryption

5468652071756663 38413d4ba2325cf1
6b2062726f776e20 141f707471ac2ced
666f78206a756d70 57db530f0123b5ac

Decryption

38413d4ba2325cf1 5468652071756663
141f707471ac2ced 6b2062726f776e20
57db530f0123b5ac 666f78206a756d70




My Correction Test String
Test String: The quick brown fox jump

Encryption

5468652071756963 1ccf23869d09333e
6b2062726f776e20 cce21c8112256fe6
666f78206a756d70 68d5c05dd9b6b900

Decryption

1ccf23869d09333e 5468652071756963
cce21c8112256fe6 6b2062726f776e20
68d5c05dd9b6b900 666f78206a756d70

CBC Mode

Encryption

5468652071756963 5ba523a59a510971
6b2062726f776e20 0da06400f058192a
666f78206a756d70 743dc4df1c592655

Decryption

5ba523a59a510971 5468652071756963
0da06400f058192a 6b2062726f776e20
743dc4df1c592655 666f78206a756d70

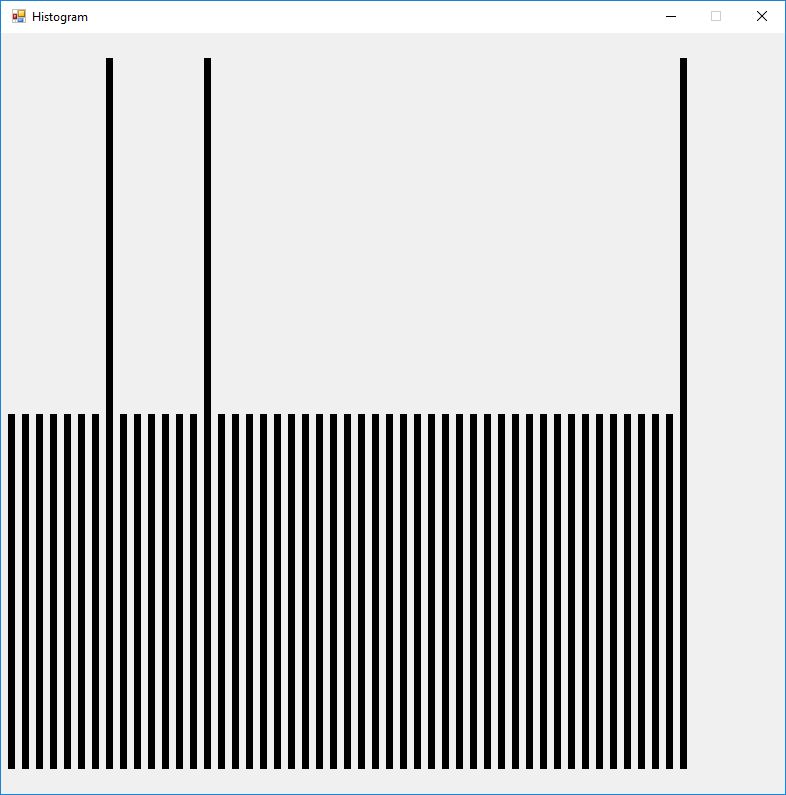
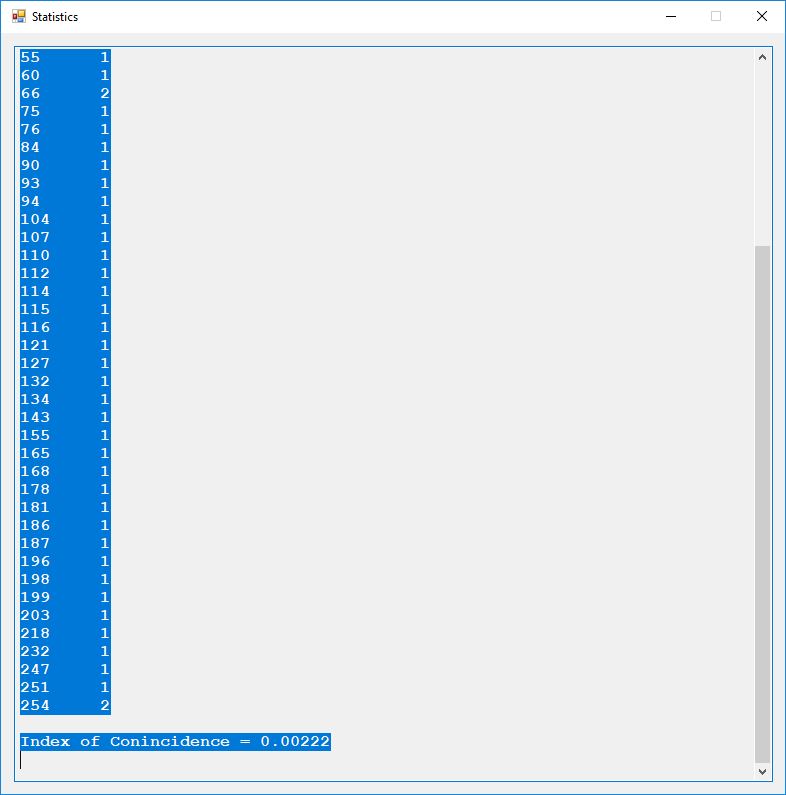
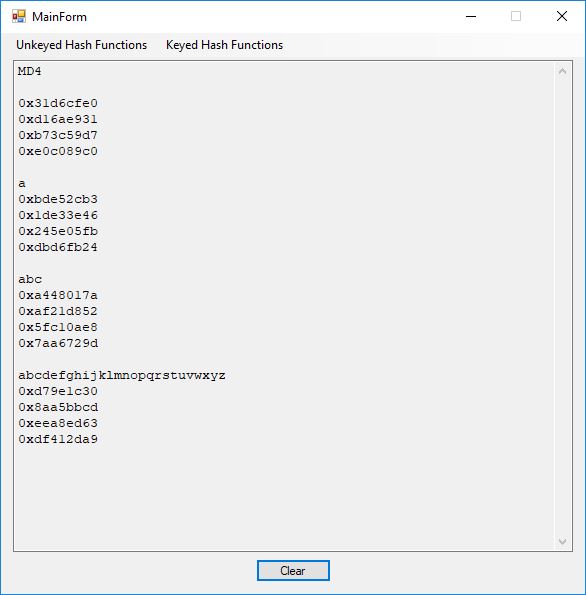
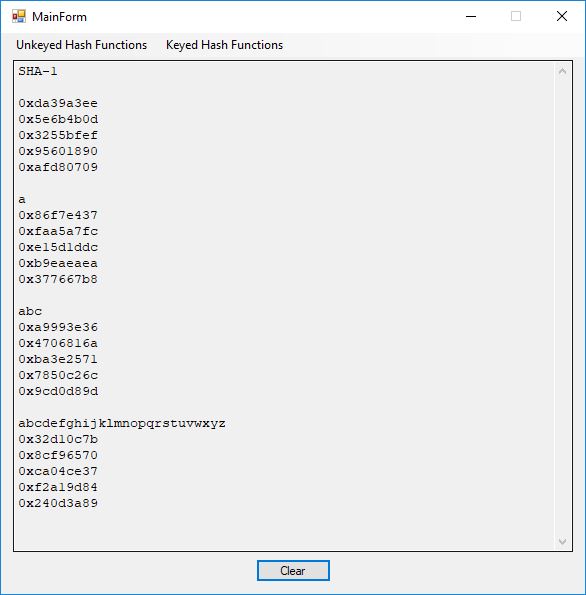
The DES test output is illustrated as follows:

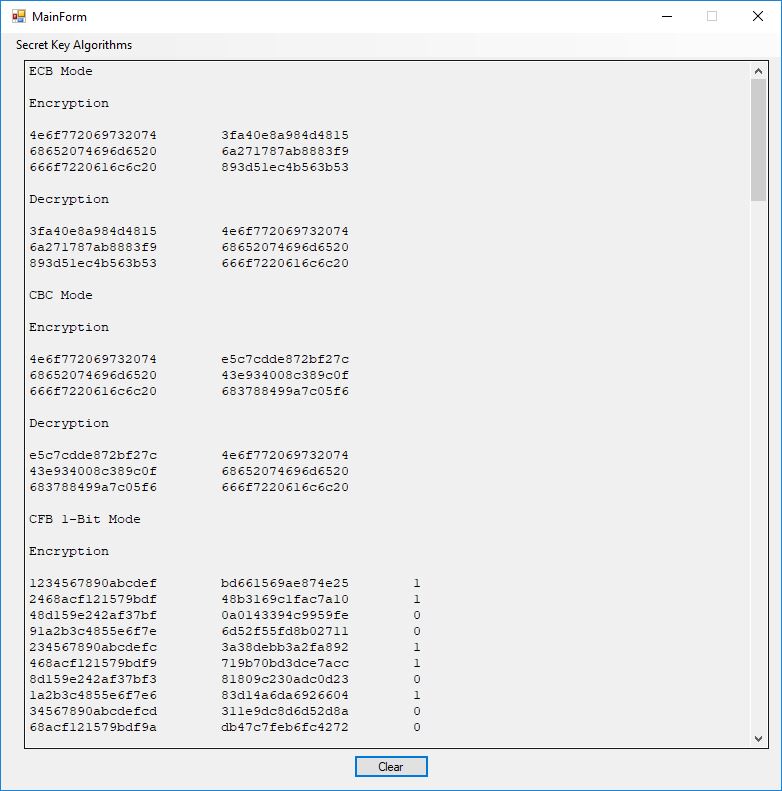
DES Chapter 7

All of the numbers from DES (Date Encryption Standard) test are given below:

ECB Mode

Encryption

4e6f772069732074 3fa40e8a984d4815
68652074696d6520 6a271787ab8883f9
666f7220616c6c20 893d51ec4b563b53

Decryption

3fa40e8a984d4815 4e6f772069732074
6a271787ab8883f9 68652074696d6520
893d51ec4b563b53 666f7220616c6c20

CBC Mode

Encryption

4e6f772069732074 e5c7cdde872bf27c
68652074696d6520 43e934008c389c0f
666f7220616c6c20 683788499a7c05f6

Decryption

e5c7cdde872bf27c 4e6f772069732074
43e934008c389c0f 68652074696d6520
683788499a7c05f6 666f7220616c6c20

CFB 1-Bit Mode

Encryption

1234567890abcdef bd661569ae874e25 1
2468acf121579bdf 48b3169c1fac7a10 1
48d159e242af37bf 0a0143394c9959fe 0
91a2b3c4855e6f7e 6d52f55fd8b02711 0
234567890abcdefc 3a38debb3a2fa892 1
468acf121579bdf9 719b70bd3dce7acc 1
8d159e242af37bf3 81809c230adc0d23 0
1a2b3c4855e6f7e6 83d14a6da6926604 1
34567890abcdefcd 311e9dc8d6d52d8a 0
68acf121579bdf9a db47c7feb6fc4272 0
d159e242af37bf34 b73850afa3b8ed89 0
a2b3c4855e6f7e68 f5fb19dd00590800 1
4567890abcdefcd1 0f4351a9bbffe5a5 1
8acf121579bdf9a3 769593c58e20d41b 1
159e242af37bf347 0e949d3f3a293d64 1
2b3c4855e6f7e68f 921eb7ffeacd0db9 0
567890abcdefcd1e d2ad109c8895fb95 1
acf121579bdf9a3d 3c36317828a9bd04 1
59e242af37bf347b e7248586e7e4ecac 0
b3c4855e6f7e68f6 f9a58e16a7597c5e 0
67890abcdefcd1ec e939fdf63d177946 1
cf121579bdf9a3d9 f325eac046bad58d 0
9e242af37bf347b2 8385a6d975ffdbba 0
3c4855e6f7e68f64 70a54baceae7ba6b 1

Decryption

1234567890abcdef bd661569ae874e25 0
2468acf121579bdf 48b3169c1fac7a10 1
48d159e242af37bf 0a0143394c9959fe 0
91a2b3c4855e6f7e 6d52f55fd8b02711 0
234567890abcdefc 3a38debb3a2fa892 1
468acf121579bdf9 719b70bd3dce7acc 1
8d159e242af37bf3 81809c230adc0d23 1
1a2b3c4855e6f7e6 83d14a6da6926604 0
34567890abcdefcd 311e9dc8d6d52d8a 0
68acf121579bdf9a db47c7feb6fc4272 1
d159e242af37bf34 b73850afa3b8ed89 1
a2b3c4855e6f7e68 f5fb19dd00590800 0
4567890abcdefcd1 0f4351a9bbffe5a5 1
8acf121579bdf9a3 769593c58e20d41b 1
159e242af37bf347 0e949d3f3a293d64 1
2b3c4855e6f7e68f 921eb7ffeacd0db9 1
567890abcdefcd1e d2ad109c8895fb95 0
acf121579bdf9a3d 3c36317828a9bd04 1
59e242af37bf347b e7248586e7e4ecac 1
b3c4855e6f7e68f6 f9a58e16a7597c5e 1
67890abcdefcd1ec e939fdf63d177946 0
cf121579bdf9a3d9 f325eac046bad58d 1
9e242af37bf347b2 8385a6d975ffdbba 1
3c4855e6f7e68f64 70a54baceae7ba6b 1

CFB 8-Bit Mode

Encryption

1234567890abcdef bd661569ae874e25 f3
34567890abcdeff3 7039546f9a0f6330 1f
567890abcdeff31f ad1b78b0bb371be7 da
7890abcdeff31fda 27350b01d5ca31f7 07
90abcdeff31fda07 68863426e397685d 01
abcdeff31fda0701 6798240e8c6b685f 14
cdeff31fda070114 421feefb3f8ca64f 62
eff31fda07011462 9a169a9b50666575 ee
f31fda07011462ee 703b1799be9a5748 18
1fda07011462ee18 1a4aee195be70077 7f

Decryption

1234567890abcdef bd661569ae874e25 4e
34567890abcdeff3 7039546f9a0f6330 6f
567890abcdeff31f ad1b78b0bb371be7 77
7890abcdeff31fda 27350b01d5ca31f7 20
90abcdeff31fda07 68863426e397685d 69
abcdeff31fda0701 6798240e8c6b685f 73
cdeff31fda070114 421feefb3f8ca64f 20
eff31fda07011462 9a169a9b50666575 74
f31fda07011462ee 703b1799be9a5748 68
1fda07011462ee18 1a4aee195be70077 65

CFB 64-Bit Mode

Encryption

1234567890abcdef bd661569ae874e25 f3096249c7f46e51
f3096249c7f46e51 cefba3ef73ff92a4 a69e839b1a92f784
a69e839b1a92f784 65290313e8e2ca02 03467133898ea622

Decryption

1234567890abcdef bd661569ae874e25 4e6f772069732074
f3096249c7f46e51 cefba3ef73ff92a4 68652074696d6520
a69e839b1a92f784 65290313e8e2ca02 666f7220616c6c20

OFB ISO 10116 64-Bit Mode

Encryption

1234567890abcdef bd661569ae874e25 f3096249c7f46e51
bd661569ae874e25 5d976a504786581f 35f24a242eeb3d3f
5d976a504786581f 5b0229c3443694e3 3d6d5be3255af8c3

Decryption

1234567890abcdef bd661569ae874e25 4e6f772069732074
bd661569ae874e25 5d976a504786581f 68652074696d6520
5d976a504786581f 5b0229c3443694e3 666f7220616c6c20

OFB FIPS-81 1-Bit Mode

Encryption

1234567890abcdef bd661569ae874e25 1
2468acf121579bdf 48b3169c1fac7a10 1
48d159e242af37be 8879ea93c63d77a5 1
91a2b3c4855e6f7d 0d36e16101e86d61 0
234567890abcdefa e9eab8cfc00f4ac3 0
468acf121579bdf5 9d41640f97df7904 0
8d159e242af37beb 32f72fd1899eda45 1
1a2b3c4855e6f7d6 ca2a095d20f4e769 1
34567890abcdefad de869588355e1041 1
68acf121579bdf5b 11245e6a8720ddce 1
d159e242af37beb6 836b0be324094a97 0
a2b3c4855e6f7d6d c07714703b296a5a 1
4567890abcdefadb bf6380ecc196d599 0
8acf121579bdf5b7 96ed6856969aef13 0
159e242af37beb6f 3823feaa3d170085 1
2b3c4855e6f7d6de 2d57dc0c899d6700 1
567890abcdefadbc 2fe1c261c0e1a302 0
acf121579bdf5b78 778ad641faa047d0 1
59e242af37beb6f0 f66ae4359eec3755 0
b3c4855e6f7d6de1 cd0bda27e32a13da 0
67890abcdefadbc3 9f71f74488551801 1
cf121579bdf5b787 a62e89aa6b85be74 0
9e242af37beb6f0f 7b0b2e1de987b804 1
3c4855e6f7d6de1e 7f41b5ef07c3ea29 1

Decryption

1234567890abcdef bd661569ae874e25 0
2468acf121579bdf 48b3169c1fac7a10 1
48d159e242af37be 8879ea93c63d77a5 0
91a2b3c4855e6f7d 0d36e16101e86d61 0
234567890abcdefa e9eab8cfc00f4ac3 1
468acf121579bdf5 9d41640f97df7904 1
8d159e242af37beb 32f72fd1899eda45 1
1a2b3c4855e6f7d6 ca2a095d20f4e769 0
34567890abcdefad de869588355e1041 0
68acf121579bdf5b 11245e6a8720ddce 1
d159e242af37beb6 836b0be324094a97 1
a2b3c4855e6f7d6d c07714703b296a5a 0
4567890abcdefadb bf6380ecc196d599 1
8acf121579bdf5b7 96ed6856969aef13 1
159e242af37beb6f 3823feaa3d170085 1
2b3c4855e6f7d6de 2d57dc0c899d6700 1
567890abcdefadbc 2fe1c261c0e1a302 0
acf121579bdf5b78 778ad641faa047d0 1
59e242af37beb6f0 f66ae4359eec3755 1
b3c4855e6f7d6de1 cd0bda27e32a13da 1
67890abcdefadbc3 9f71f74488551801 0
cf121579bdf5b787 a62e89aa6b85be74 1
9e242af37beb6f0f 7b0b2e1de987b804 1
3c4855e6f7d6de1e 7f41b5ef07c3ea29 1

OFB 8-Bit FIPS-81 Mode

Encryption

1234567890abcdef bd661569ae874e25 f3
34567890abcdefbd 25e73b5d4cbd2359 4a
567890abcdefbd25 5f970070553623d0 28
7890abcdefbd255f 704ad48bf9eec8fa 50
90abcdefbd255f70 a0b1a091bb787553 c9
abcdefbd255f70a0 b58127681139ee7f c6
cdefbd255f70a0b5 694d556ef5806a65 49
efbd255f70a0b569 f1885324299132a2 85
bd255f70a0b569f1 be639ff6d7b74b04 d6
255f70a0b569f1be e17b6ae22b4bad65 84

Decryption

1234567890abcdef bd661569ae874e25 4e
34567890abcdefbd 25e73b5d4cbd2359 6f
567890abcdefbd25 5f970070553623d0 77
7890abcdefbd255f 704ad48bf9eec8fa 20
90abcdefbd255f70 a0b1a091bb787553 69
abcdefbd255f70a0 b58127681139ee7f 73
cdefbd255f70a0b5 694d556ef5806a65 20
efbd255f70a0b569 f1885324299132a2 74
bd255f70a0b569f1 be639ff6d7b74b04 68
255f70a0b569f1be e17b6ae22b4bad65 65

The results of Section 7.5 FEAL (Fast Data Encipherment Algorithm) in particular 7.99 Example page 262 are shown below:

FEAL Chapter 7

Here are the numbers of the 7.99 Example copied from the preceding application’s text box:

0xDF3B
0xCA36
0xF17C
0x1AEC
0x45A5
0xB9C7
0x26EB
0xAD25
0x8B2A
0xECB7
0xAC50
0x9D4C
0x22CD
0x479B
0xA8D5
0x0CB5
0xCEEF2C86 0xF2490752
0x00000000 0x00000000

Moving on to Section 7.6 IDEA (International Data Encryption Algorithm) a 64-bit block cipher:

IDEA Chapter 7

Again for clarity we reproduce the preceding numbers below see Table 7.12 page 265 and Table 7.13 page 266\:

1 0x0001 0x0002 0x0003 0x0004 0x0005 0x0006 0x00F0 0x00F5 0x010A 0x0105
2 0x0007 0x0008 0x0400 0x0600 0x0800 0x0A00 0x222F 0x21B5 0xF45E 0xE959
3 0x0C00 0x0E00 0x1000 0x0200 0x0010 0x0014 0x0F86 0x39BE 0x8EE8 0x1173
4 0x0018 0x001C 0x0020 0x0004 0x0008 0x000C 0x57DF 0xAC58 0xC65B 0xBA4D
5 0x2800 0x3000 0x3800 0x4000 0x0800 0x1000 0x8E81 0xBA9C 0xF77F 0x3A4A
6 0x1800 0x2000 0x0070 0x0080 0x0010 0x0020 0x6942 0x9409 0xE21B 0x1C64
7 0x0030 0x0040 0x0050 0x0060 0x0000 0x2000 0x99D0 0xC7F6 0x5331 0x620E
8 0x4000 0x6000 0x8000 0xA000 0xC000 0xE001 0xD98D 0xD331 0xD002 0x754C
9 0x0080 0x00C0 0x0100 0x0140 0x0000 0x0000 0xC614 0xD0C2 0xD431 0x9E6E
1 0xFE01 0xFF40 0xFF00 0x659A 0xC000 0xE001 0x0000 0xD331 0xD002 0x754C
2 0xFFFD 0x8000 0xA000 0xCCCC 0x0000 0x2000 0x0ECF 0x7ECD 0xCDFF 0x3475
3 0xA556 0xFFB0 0xFFC0 0x52AB 0x0010 0x0020 0x68EA 0xFFAF 0xD82A 0xD560
4 0x554B 0xFF90 0xE000 0xFE01 0x0800 0x1000 0x531C 0xA0AC 0x6FD6 0x90E9
5 0x332D 0xC800 0xD000 0xFFFD 0x0008 0x000C 0x3E10 0x1E89 0x4E8A 0x2626
6 0x4AAB 0xFFE0 0xFFE4 0xC001 0x0010 0x0014 0x11F2 0x5D0A 0xFC89 0x6B6A
7 0xAA96 0xF000 0xF200 0xFF81 0x0800 0x0A00 0x8177 0x4429 0xD97C 0xDF40
8 0x4925 0xFC00 0xFFF8 0x552B 0x0005 0x0006 0x35AB 0x6CE9 0x33CF 0x069D
9 0x0001 0xFFFE 0xFFFD 0xC001 0x0000 0x0000 0x35AB 0x33CD 0x6CE6 0xC1A8

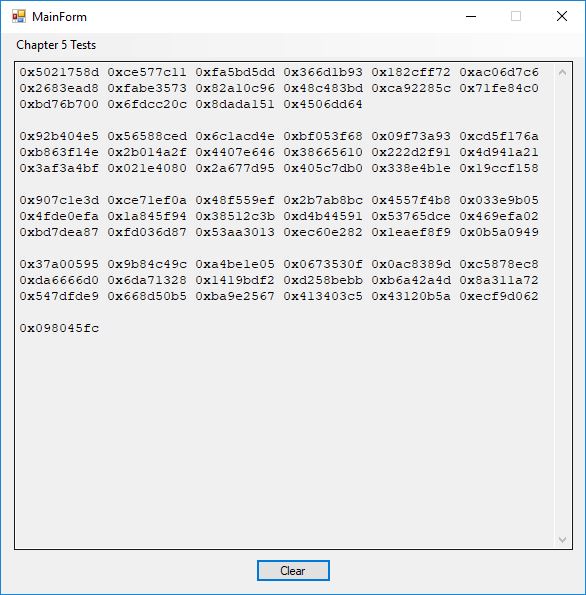
Finally the results from Section 7.7 on SAFER, RC5, etc.

SAFER Chapter 7

See 7.114 Example page 269.

Encryption results
200 242 156 221 135 120 62 217 
Decryption results
 1 2 3 4 5 6 7 8

RC5 application results:

RC5 Chapter 7

See 7.118 Example page 270:

0x15E444EB 0x249831DA
0xB278C165 0xCC97D18

Chapter 6 of the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone Highlights by James Pate Williams, Jr. BA, BS, MSwE, PhD

In my opinion the key section of Chapter 6 of the Handbook is 6.4.1 that covers the SEAL (Software-optimized Encryption Algorithm) stream cipher. My original C implementation of SEAL was probably created in period 1996 to 1998. In February 2017, I created a C# implementation of the algorithm. Below is the output from the SEAL test.

SEAL Test

For clarity I reproduce the numbers above text box in the text area that follows:

0x5021758d 0xce577c11 0xfa5bd5dd 0x366d1b93 0x182cff72 0xac06d7c6 
0x2683ead8 0xfabe3573 0x82a10c96 0x48c483bd 0xca92285c 0x71fe84c0 
0xbd76b700 0x6fdcc20c 0x8dada151 0x4506dd64

0x92b404e5 0x56588ced 0x6c1acd4e 0xbf053f68 0x09f73a93 0xcd5f176a 
0xb863f14e 0x2b014a2f 0x4407e646 0x38665610 0x222d2f91 0x4d941a21 
0x3af3a4bf 0x021e4080 0x2a677d95 0x405c7db0 0x338e4b1e 0x19ccf158

0x907c1e3d 0xce71ef0a 0x48f559ef 0x2b7ab8bc 0x4557f4b8 0x033e9b05 
0x4fde0efa 0x1a845f94 0x38512c3b 0xd4b44591 0x53765dce 0x469efa02 
0xbd7dea87 0xfd036d87 0x53aa3013 0xec60e282 0x1eaef8f9 0x0b5a0949

0x37a00595 0x9b84c49c 0xa4be1e05 0x0673530f 0x0ac8389d 0xc5878ec8 
0xda6666d0 0x6da71328 0x1419bdf2 0xd258bebb 0xb6a42a4d 0x8a311a72 
0x547dfde9 0x668d50b5 0xba9e2567 0x413403c5 0x43120b5a 0xecf9d062

0x098045fc

The preceding numbers reproduce the 6.70 Example on pages 215-216 of the Handbook. The first block of hex digits is the R table. The second set of hex digits is the T table. The third set of hex digits is the word S[0], S[1], …, S[255]. The penultimate set of hex digits is the part of the 1024 words of the y output vector. The last hex encoded number is the XOR of the 1024 y output vector numbers.