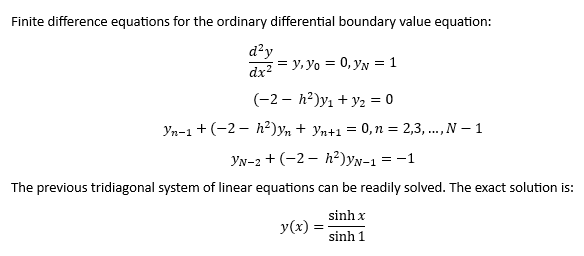Category: Matrix Algebra
Several Problems from Schiff Chapter 7 (c) May 19-24, 2024, by James Pate Williams, Jr.
A Few Problems from Schiff Chapter 6 (c) May 19-20, 2024, by James Pate Williams, Jr.
A Matrix Identity

Preliminary Factorization Results of the Thirteenth Fermat Number (c) February 5, 2024, by James Pate Williams, Jr.
I am working on a factorization of the Thirteenth Fermat number which is 2 ^ 8192 + 1 and is 2,467 decimal digits in length. I am using Pollard’s factoring with cubic integers on the number (2 ^ 2731) ^ 3 + 2. I am also utilizing a homegrown variant of the venerable Pollard and Brent rho method and Arjen K. Lenstra’s Free LIP Elliptic Curve Method. I can factor the seventh Fermat number 2 ^ 128 + 1 in five to thirty minutes using my C# code. The factoring with cubic integers code is in C and uses Free-LIP.
Fermat factoring status (prothsearch.com)
The following is a run of Lenstra’s ECM algorithm:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^8192+1
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 1
2710954639361 p # digits 13
3603109844542291969 p # digits 19
Runtime (s) = 17015.344000
I aborted the previous computation due to the fact I was curious about the number of prime factors that could be found on personal computer. I will try a lot more calculation time in a future run. My homegrown application is able to at least find the first factor of Fermat Number 13.
Latest Factoring Results (c) February 4, 2024, by James Pate Williams, Jr.
I am testing two factoring algorithms: Pollard-Shor-Williams’s method, a home-grown version of the venerable Pollard rho algorithm and Pollard’s factoring with cubic integers. The second recipe is from “The Development of the Number Field Sieve” edited by Arjen K. Lenstra and Hendrik W. Lenstra, Jr. I use the 20-digit test number, 2 ^ 66 + 2 = 73786976294838206466. My method is very fast with this number as shown below:
2^66+2
73786976294838206466 20
Pseudo-Random Number Generator Seed = 1
Number of Tasks = 1
2 p 1
3 p 1
11 p 2
131 p 3
2731 p 4
409891 p 6
7623851 p 7
Elapsed hrs:min:sec.MS = 00:00:00.652
Function Evaluations = 1995
The Pollard factoring with cubic integers takes a long time but is capable of factoring much larger numbers. The results of the full factorization of my test number are:
== Data Menu ==
1 Simple Number
2 Fibonacci Sequence Number
3 Lucas Sequence Number
4 Exit
Enter option (1 – 4): 1
Enter a number to be factored: 2^66+2
Enter a random number generator seed: 1
== Factoring Menu ==
1 Lenstra’s ECM
2 Lenstra’s Pollard-Rho
3 Pollard’s Factoring with Cubic Integers
Option (1 – 3): 3
73786976294838206466
Enter a lower bound : -50000
Enter a upper bound : +50000
Enter b lower bound : +1
Enter b upper bound : +50000
Enter maximum kernels : 1024
Enter algebraic prime count: 300
Enter rational prime count: 300
Enter lo large prime bound: 10000
Enter hi large prime bound: 11000
Numbers sieved = 452239293
Successes 0 gcd(a, b) is 1 = 274929004
Successes 1 rational smooth a + b * r = 181838258
Successes 2 long long smooth = 68959
Successes 3 kernels tested = 535
2 p # digits 1
3 p # digits 1
11 p # digits 2
131 p # digits 3
2731 p # digits 4
409891 p # digits 6
7623851 p # digits 7
Runtime (s) = 36383.696000
It took over ten hours to fully factor, 2 ^ 66 + 2. I am currently attempting to factor the Thirteenth Fermat number which is 2 ^ (2 ^ 13) + 1 = 2 ^ 8192 + 1. The number has 2,467 decimal digits. I am using 399 algebraic prime numbers, 600 rational prime numbers, and 316 “large prime numbers” (primes between 12,000 and 15,000). I have to find the kernels of a 1316 by 1315 matrix. I am trying the factorization using a maximum of 8192 kernels. I suspect this computation will take about a week on my desktop workstation. There is no guarantee that I will find a non-trivial factor of 2 * (2731 ^ 3) + 2.
Fast and Slow Matrix Multiplication by James Pate Williams, Jr. © January 13, 2024, All Applicable Rights Reserved
Note: For comparison with a paper on matrix operations, we use column major order also known as column major echelon order. Column major order is used in Fortran and row major order is utilized in C computations.
Here is the supposedly slow C source code:
void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
double t = 0;
for (int k = 1; k <= n; k++)
t += a[i][k] * b[k][j];
c[i][j] = t;
}
}
}
And now we present the allegedly fast multiplication code:
void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
double t = b[k][j];
for (int i = 1; i <= n; i++)
c[i][j] += a[i][k] * t;
}
}
}
Finally, we have another algorithm for matrix multiplication:
void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
for (int k = 1; k <= n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
}
We performed the following experiments.
slow runtime in microseconds: 2736
semi runtime in microseconds: 4001
fast runtime in microseconds: 5293
n * n = 10000
equal = 10000
n * n = 10000
equal = 10000
slow runtime in microseconds: 21962
semi runtime in microseconds: 29585
fast runtime in microseconds: 28701
n * n = 40000
equal = 40000
n * n = 40000
equal = 40000
slow runtime in microseconds: 67256
semi runtime in microseconds: 101554
fast runtime in microseconds: 107969
n * n = 90000
equal = 90000
n * n = 90000
equal = 90000
slow runtime in microseconds: 183839
semi runtime in microseconds: 268616
fast runtime in microseconds: 244832
n * n = 160000
equal = 160000
n * n = 160000
equal = 160000
slow runtime in microseconds: 428263
semi runtime in microseconds: 638721
fast runtime in microseconds: 650535
n * n = 250000
equal = 250000
n * n = 250000
equal = 250000
C:\Users\james\source\repos\FastMatrixMultiplication\Debug\FastMatrixMultiplication.exe (process 29552) exited with code 0.
Press any key to close this window . . .
// FastMatrixMultiplication.cpp : This file contains the 'main' function. Program execution begins and ends there.
// https://www-users.york.ac.uk/~mijp1/teaching/grad_HPC_for_MatSci/Lecture4.pdf
// https://stackoverflow.com/questions/25483620/how-to-measure-running-time-of-specific-function-in-c-very-accurate
#include <stdlib.h>
#include <chrono>
#include <iostream>
using namespace std;
typedef chrono::high_resolution_clock Clock;
void ColMajorFastMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
double t = b[k][j];
for (int i = 1; i <= n; i++)
c[i][j] += a[i][k] * t;
}
}
}
void ColMajorSemiMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
for (int k = 1; k <= n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
}
void ColMajorSlowMatMul(double** a, double** b, double** c, int n)
{
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
c[j][k] = 0.0;
for (int j = 1; j <= n; j++)
{
for (int i = 1; i <= n; i++)
{
double t = 0;
for (int k = 1; k <= n; k++)
t += a[i][k] * b[k][j];
c[i][j] = t;
}
}
}
void GenerateMatrix(double** a, int n, int seed)
{
srand(seed);
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
a[j][k] = (double)rand() / RAND_MAX;
}
}
}
int main()
{
for (int n = 100; n <= 500; n += 100)
{
double** a = new double* [n + 1];
double** b = new double* [n + 1];
double** c = new double* [n + 1];
double** d = new double* [n + 1];
double** e = new double* [n + 1];
for (int j = 0; j < n + 1; j++)
{
a[j] = new double[n + 1];
b[j] = new double[n + 1];
c[j] = new double[n + 1];
d[j] = new double[n + 1];
e[j] = new double[n + 1];
}
GenerateMatrix(a, n, 1);
GenerateMatrix(b, n, 2);
auto clock1 = Clock::now();
ColMajorSlowMatMul(a, b, c, n);
auto clock2 = Clock::now();
long long microseconds1 = chrono::duration_cast<chrono::microseconds>
(clock2 - clock1).count();
auto clock3 = Clock::now();
ColMajorSemiMatMul(a, b, d, n);
auto clock4 = Clock::now();
long long microseconds2 = chrono::duration_cast<chrono::microseconds>
(clock4 - clock3).count();
auto clock5 = Clock::now();
ColMajorFastMatMul(a, b, e, n);
auto clock6 = Clock::now();
long long microseconds3 = chrono::duration_cast<chrono::microseconds>
(clock6 - clock5).count();
cout << "slow runtime in microseconds: " << microseconds1 << endl;
cout << "semi runtime in microseconds: " << microseconds2 << endl;
cout << "fast runtime in microseconds: " << microseconds3 << endl;
long long equal = 0;
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (c[j][k] == d[j][k])
equal++;
cout << "n * n = " << n * n << endl;
cout << "equal = " << equal << endl;
equal = 0;
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (c[j][k] == e[j][k])
equal++;
cout << "n * n = " << n * n << endl;
cout << "equal = " << equal << endl;
for (int j = 0; j < n + 1; j++)
{
delete[] a[j];
delete[] b[j];
delete[] c[j];
delete[] d[j];
delete[] e[j];
}
delete[] a;
delete[] b;
delete[] c;
delete[] d;
delete[] e;
}
}
Comparison of Linear Systems Applications in C# and C++ by James Pate Williams, Jr.
Back in 2017 I created a C# application that implemented the direct methods: Cholesky decomposition, Gaussian elimination with partial pivoting, LU decomposition, and simple Gaussian elimination. The classical iterative methods Gauss-Seidel, Jacobi, Successive Overrelaxation, and gradient descent were also implemented along with the modern iterative methods: conjugate gradient descent and Modified Richardson’s method. Recently I translated the C# code to C++. I used the following test matrices: Cauchy, Lehmer, Pascal, and other. Below are some results. As is apparent the C++ runtimes are faster than the C# execution times.
Richardson Method Translated from C Source Code to C# by James Pate Williams, Jr.


The Richardson Method is called before eliminating the system of linear equations.
Added elimination results from a vanilla C program and a C# application.


These results are not in total agreement with H. T. Lau’s results.
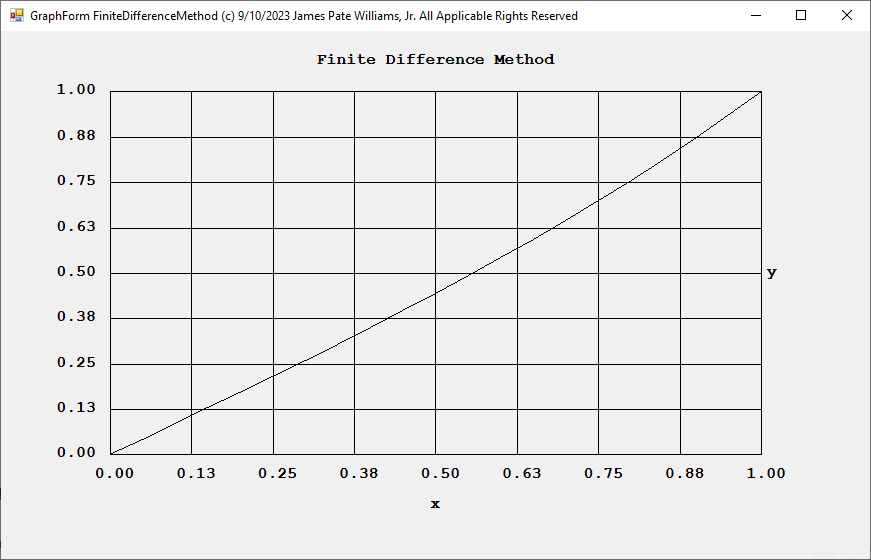
Finite Difference Method for Solving Second Order Ordinary Differential Equations by James Pate Williams, Jr.
My reference is Numerical Analysis: An Algorithmic Approach 3rd Edition by S. D. Conte and Carl de Boor Chapter 9.1.