Solve for a real root of the equation
f(x)=log6l(5+x)+log6l(x)=0
First we test our log6l(x) function
log6l(12) = 1.386853
log6l(36) = 2.000000
x = 0.1925824036
f = 0.0000000000
Category: Memoirs of James Pate Williams Jr
Blog Entry (c) Friday August 30, 2024, by James Pate Williams, Jr. Another Simple Math Problem
We use an evolutionary hill-climber and the solution of the quadratic equation to solve the easy problem below:
Solution of f(a,x)=sin(sqrt(ax-x^2))=0
Subject to the constraint x+y=100
Where x and y are the two roots of
g(a,x)=ax-x^2-n*n*pi*pi=0
and n=15
a = 100.347888933988
x = 32.947113268776
y = 67.400775665213
g = 0.000000000000
s = 100.347888933988
runtime in seconds = 43.730000
Blog Entry (c) Wednesday August 28, 2024, by James Pate Williams, Jr.
Blog Entry (c) Tuesday, August 27, 2024, Two More Online Mathematics Problems by James Pate Williams, Jr.
Solution of f(t) = cos(2t) + cos(3t)
t = 0.628318530718
f(t) = 1.11022302e-16
Solution of f(x) = sqrt(1 + sqrt(1 + x)) - x^1/3
x = 8.000000000000
f(x) = 0.00000000e+00
Solution of f(x) = 9^x + 12^x - 16^x
x = -16.387968065352
f(x) = 2.32137533e-16
Solution of f(x) = 8^x-2^x - 2(6^x-3^x)
x = 1.000000000000
f(x) = 0.00000000e+00
Blog Entry (c) Tuesday, August 27, 2024, Graphing New Goldwasser-Kilian Primality Test Results by James Pate Williams, Jr.
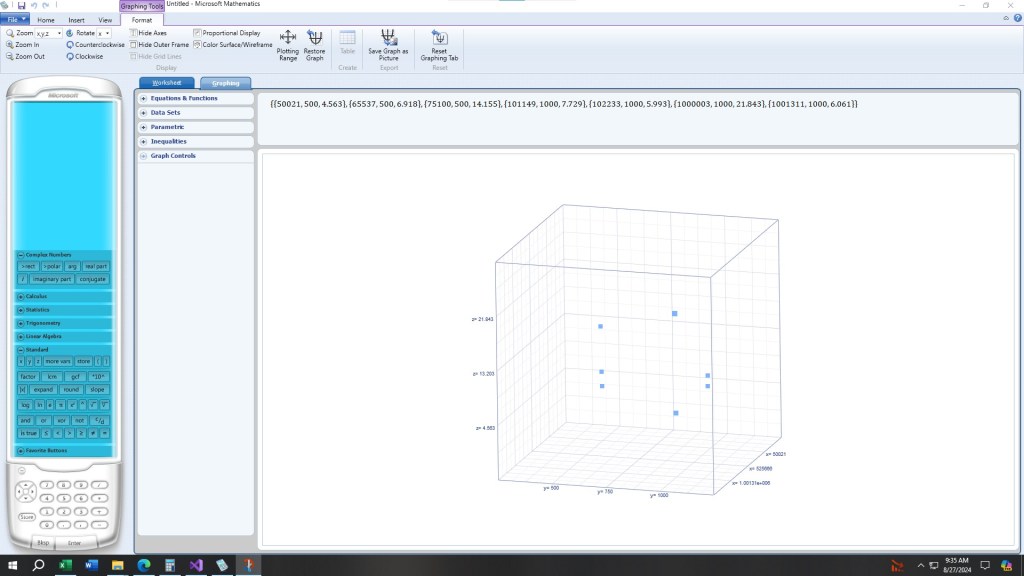
The x -axis is the number to be tested, the y-axis is prime number bound for factoring, and the z-axis is the runtime in seconds.
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. New and Improved Version of the Goldwasser-Kilian Primality Test
I corrected my powering modulo a prime routine. I added Pollard’s p – 1 factoring method and Shanks-Mestre elliptic curve point counting algorithm.
number to be tested or 0 to quit:
10000019
number of primes in factor base:
10000
Prime sieving time = 3.220000
N[0] = 10000019
a = 7838973
b = 2449531
m = 9995356
q = 356977
P = (9786147, 3226544)
P1 = (0, 1)
P2 = (5887862, 8051455)
N[1] = 356977
a = 45561
b = 178451
m = 357946
q = 178973
P = (80627, 163299)
P1 = (0, 1)
P2 = (52101, 282559)
N[2] = 178973
a = 135281
b = 76426
m = 178996
q = 73
P = (10238, 98035)
P1 = (0, 1)
P2 = (46702, 94326)
number is proven prime
runtime in seconds = 35.471000
number to be tested or 0 to quit:
10015969
number of primes in factor base:
10000
Prime sieving time = 3.424000
N[0] = 10015969
a = 6613193
b = 3951715
m = 10013908
q = 2503477
P = (998314, 8329764)
P1 = (0, 1)
P2 = (6944357, 1053776)
N[1] = 2503477
a = 1175442
b = 379813
m = 2505736
q = 293
P = (646462, 1631861)
P1 = (0, 1)
P2 = (1477980, 88719)
number is proven prime
runtime in seconds = 5.612000
number to be tested or 0 to quit:
99997981
number of primes in factor base:
10000
Prime sieving time = 4.152000
N[0] = 99997981
a = 34129462
b = 80482974
m = 100001414
q = 181
P = (19305995, 40493835)
P1 = (0, 1)
P2 = (33828245, 72969559)
number is proven prime
runtime in seconds = 11.500000
number to be tested or 0 to quit:
100001819
number of primes in factor base:
100000
Prime sieving time = 3.218000
N[0] = 100001819
a = 2694060
b = 17329746
m = 100008102
q = 5569
P = (124594, 14596756)
P1 = (0, 1)
P2 = (32514144, 56926555)
number is proven prime
runtime in seconds = 76.301000
number to be tested or 0 to quit:
100005317
number of primes in factor base:
100000
Prime sieving time = 3.269000
N[0] = 100005317
a = 45478318
b = 328034
m = 99988256
q = 3124633
P = (62548529, 30179124)
P1 = (0, 1)
P2 = (70379514, 76899689)
N[1] = 3124633
a = 2605576
b = 1809212
m = 3127654
q = 503
P = (1236288, 2081401)
P1 = (0, 1)
P2 = (2264479, 2583693)
number is proven prime
runtime in seconds = 459.979000
number to be tested or 0 to quit:
100000007
number of primes in factor base:
100000
Prime sieving time = 3.209000
N[0] = 100000007
a = 50593669
b = 72502607
m = 100005736
q = 2053
P = (72365335, 69885097)
P1 = (0, 1)
P2 = (55023241, 20078454)
number is proven prime
runtime in seconds = 163.705000
number to be tested or 0 to quit:
100014437
number of primes in factor base:
100000
Prime sieving time = 3.919000
N[0] = 100014437
a = 49955472
b = 45482796
m = 100024160
q = 263
P = (41650735, 8652103)
P1 = (0, 1)
P2 = (53790105, 37282431)
number is proven prime
runtime in seconds = 12.915000
Blog Entry (c) Wednesday, August 21, 2024, by James Pate Williams, Jr. Single Precision (64-Bit) Version of Pollard’s P-1 Factoring Method
prime number sieve creation
time in seconds = 3.483000
number to be factored or 0 to quit:
2111222333
1 11 1 p
2 17 1 p
3 11289959 1 p
factoring time in seconds = 0.063000
number to be factored or 0 to quit:
1234567890
1 2 1 p
2 3 2 p
3 5 1 p
4 3607 1 p
5 3803 1 p
factoring time in seconds = 0.133000
number to be factored or 0 to quit:
2^30+0
prime powers are not allowed
number to be factored or 0 to quit:
0
Blog Entry (c) Tuesday, August 20, 2024, by James Pate Williams, Jr. More Goldwasser-Kilian Primality Results (64-Bit Version which I call Single Precision)
Blog Entry (c) Monday, August 19, 2024, by James Pate Williams, Jr. Results from a Corrected Version of my Implementation of the 64-Bit Goldwasser-Kilian Primality Test
Blog Entry Wednesday, August 14, 2024 (c) James Pate Williams, Jr. Goldwasser-Kilian Primality Test
The Goldwasser-Kilian Primality proving algorithm was the first method to utilize elliptic curves to generate primality proving certificates. What follows is a file of two certificates and the single precision C source code.