Computerized solutions to Exercises 27.3 to 27.6:
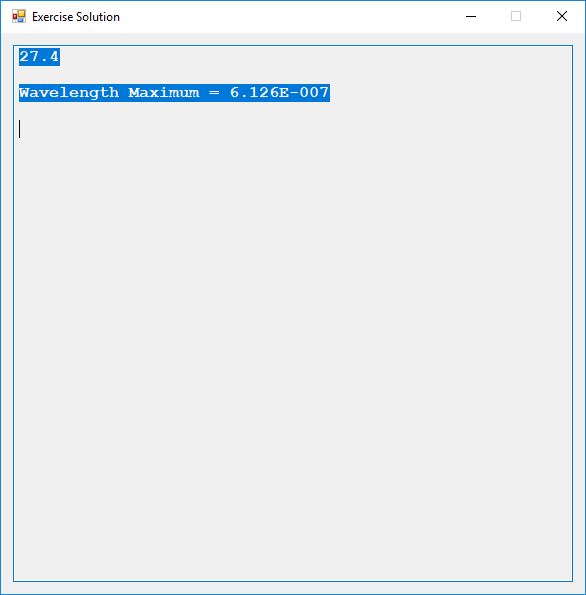
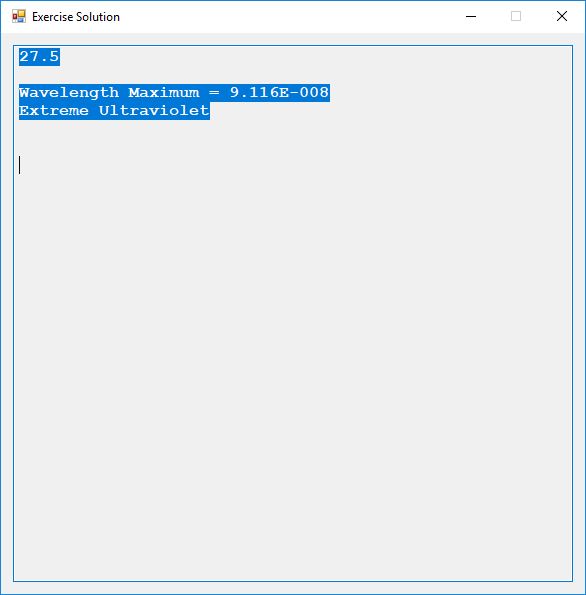
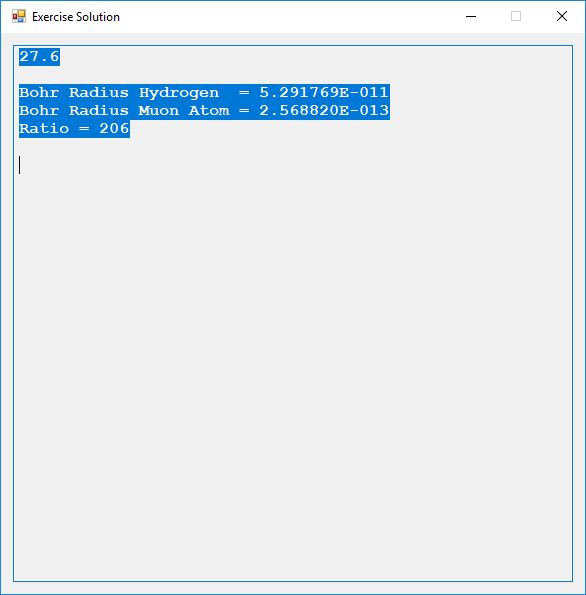
Partial source code for the preceding C# application:
Detailed solutions to Exercises 27.3 to 27.7 in a Portable Document File (PDF):
Category: Quantum Mechanics and Quantum Chemistry
Separation of Variables for the Time-Independent Schrödinger Equation for the Non-Relativistic Hydrogen-Like Atom by James Pate Williams, Jr. BA, BS, MSwE, PhD
Separation and Partial Solution of the Time Dependent Schrödinger Equation for the Non-Relativistic Hydrogen-Like Atom by James Pate Williams, Jr. BA, BS, MSwE, PhD
In the following terse document we start with the non-relativistic and time dependent Schrödinger equation for the hydrogen-like atom of atomic number Z. We then separate the equation into one ordinary differential equation eigenvalue problem involving the variable time and two partial differential equations eigenvalue problems, each with three variables. The resulting center of mass partial differential equation eigenvalue problem is separable in Cartesian coordinates. The other eigenvalue problem is not separable in Cartesian coordinates due to the nature of the potential energy function in the Hamiltonian operator. This treatment is an expansion on the excellent textbook section that is cited in the References section of the document.
Numerical Explorations 