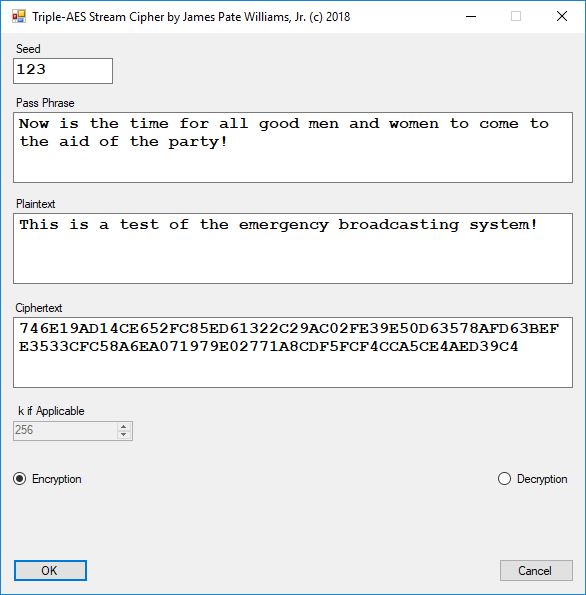
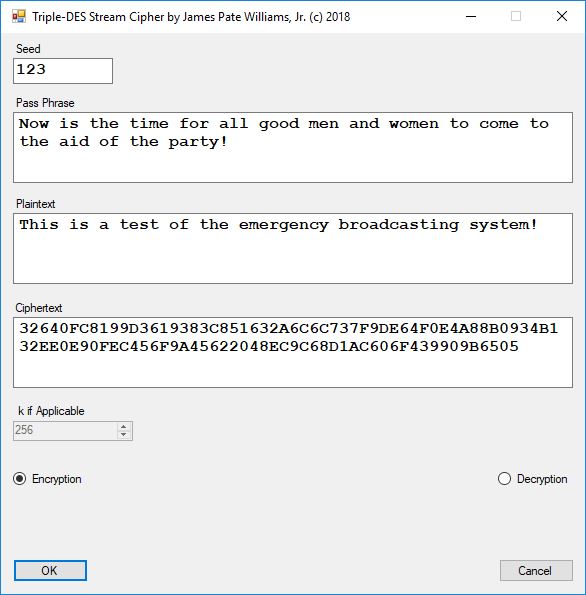
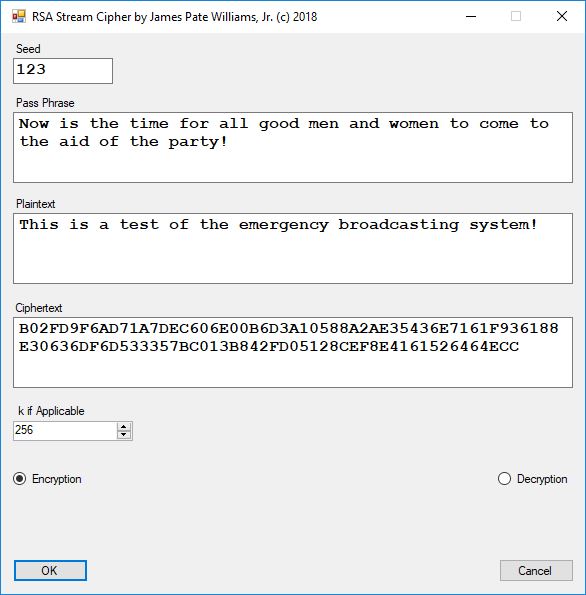
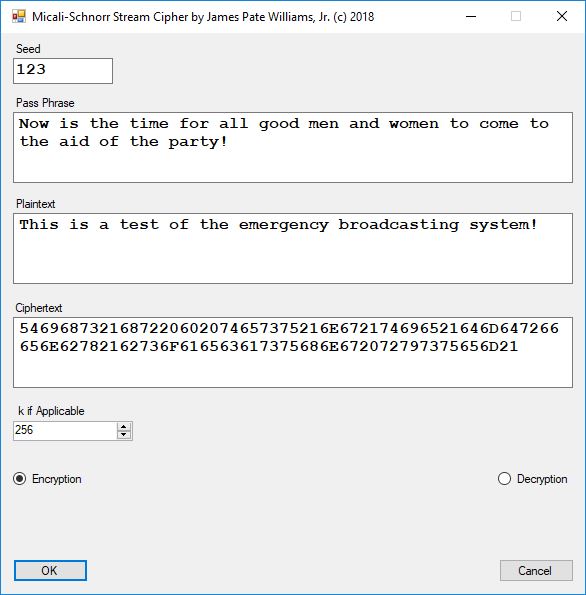
Reference: Cryptographic Standards and Guidelines | CSRC
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
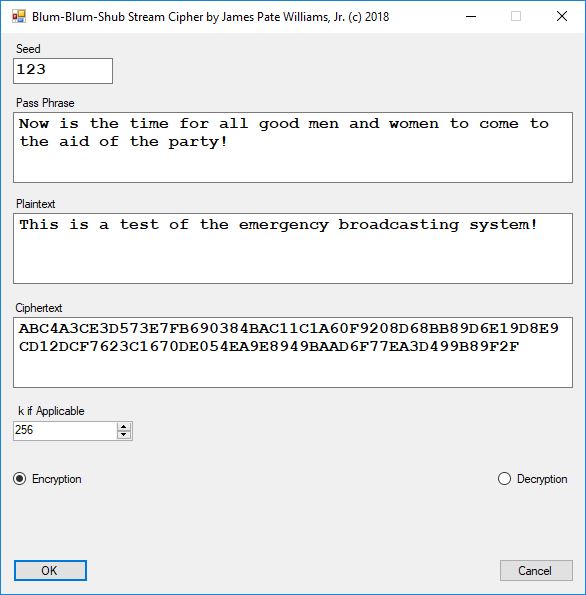
Enter option = 3
NIST Standard Test Data
128-Bit Cipher Key
2B7E1516 28AED2A6 ABF71588 09CF4F3C
Electronic Codebook (ECB) Mode
ECB-AES128 (Encryption)
NIST Standard Test Data
AES-128 (Nk = 4, Nr = 10)
Test Vectors
Round[0] Input to Cipher
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[0] After Add Round Key
40BFABF4 06EE4D30 42CA6B99 7A5C5816
Round[1] After Sub Bytes
090862BF 6F28E304 2C747FEE DA4A6A47
Round[1] After Shift Rows
09287F47 6F746ABF 2C4A6204 DA08E3EE
Round[1] After Mix Columns
529F16C2 978615CA E01AAE54 BA1A2659
Round[1] After Add Round Key
F265E8D5 1FD2397B C3B9976D 9076505C
Round[2] After Sub Bytes
894D9B03 C0B51221 2E56883C 6038534A
Round[2] After Shift Rows
89B5884A C0565303 2E389B21 604D123C
Round[2] After Mix Columns
0F31E929 319A3558 AEC95893 39F04D87
Round[2] After Add Round Key
FDF37CDB 4B0C8C1B F7FCD8E9 4AA9BBF8
Round[3] After Sub Bytes
540D10B9 B3FE64AF 68B0611E D6D3EA41
Round[3] After Shift Rows
54FE6141 B3B0EAB9 68D310AF D60D641E
Round[3] After Mix Columns
9151ABE1 E5541CFD 014A713E DA7E3134
Round[3] After Add Round Key
ACD1EC9C A242E2C3 1F690F7A B704B90F
Round[4] After Sub Bytes
913ECEDE 3A2C982E C0F976DA A9F25676
Round[4] After Shift Rows
912C7676 3AF956DE C0F2CE2E A93E98DA
Round[4] After Mix Columns
4D25CB1E ECF71646 7658C73B 49BCC9E9
Round[4] After Add Round Key
A2616E5F 44A54D39 C029E200 92B764E9
Round[5] After Sub Bytes
3AEF9FCF 1B06E312 BAA59863 4FA9431E
Round[5] After Shift Rows
3A06981E 1BA543CF BAA99F12 4FEFE363
Round[5] After Mix Columns
F89B35EC 4E40724E 025B00C7 34D7D81B
Round[5] After Add Round Key
2C4AF314 32C3EFC9 C8A9B87B 252ECDA7
Round[6] After Sub Bytes
71D60DFA 232EDFDD E8D36C21 3F31BD5C
Round[6] After Shift Rows
712E6C5C 23D3BDFA E8310DDD 3FD6DF21
Round[6] After Mix Columns
A0C56369 6FB884E4 4840BFBE E1D32F0A
Round[6] After Add Round Key
CD4DC013 7EB3BA19 93B939FF 2BD3BCF7
Round[7] After Sub Bytes
BDE3BA7D F36DF4D4 DC561216 F1666568
Round[7] After Shift Rows
BD6D1268 F356657D DC66BAD4 F1E3F416
Round[7] After Mix Columns
AC394C73 1F8DE8C7 6711B210 253DDB33
Round[7] After Add Round Key
E26DBB7D 40D22134 E3B7FDA2 6B9B077C
Round[8] After Sub Bytes
983CEAFF 09B5FD18 11A9543A 7F14C510
Round[8] After Shift Rows
98B55410 09A9C5FF 1114EA18 7F3CFD3A
Round[8] After Mix Columns
AB05B572 C8EB2B92 EC04E2FD 7D21EC34
Round[8] After Add Round Key
41D7C653 7D669140 DD2F179D 02ACC51B
Round[9] After Sub Bytes
830EB4ED FF338109 C115F05E 7791A6AF
Round[9] After Shift Rows
8333F0AF FF15A6ED C191B409 770E815E
Round[9] After Mix Columns
1741A118 91C99168 8C36386F 23AD82AA
Round[9] After Add Round Key
BB36C7EB 88334D49 A4E7112E 74F182C4
Round[10] After Sub Bytes
EA05C6E9 C4C3E33B 49948231 92A1131C
Round[10] After Shift Rows
EAC3821C C49413E9 49A1C63B 9205E331
Round[10] After Add Round Key
3AD77BB4 0D7A3660 A89ECAF3 2466EF97
Round[0] Input to Cipher
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[0] After Add Round Key
85539F41 36AD7E3A 35407A24 4C60C16D
Round[1] After Sub Bytes
97EDDB83 0595F380 9609DA36 29D0783C
Round[1] After Shift Rows
9795DA3C 05097883 96D0DB80 29EDF336
Round[1] After Mix Columns
77EFE995 EA1C6263 07DB70B1 BBD06309
Round[1] After Add Round Key
D7151782 62484ED2 24784988 91BC150C
Round[2] After Sub Bytes
0E59F013 AA522FB5 36BC3BC4 816559FE
Round[2] After Shift Rows
0E523BFE AABC5913 3665F0B5 81592FC4
Round[2] After Mix Columns
2F19339C DA319126 86426CBE 1986D17D
Round[2] After Add Round Key
DDDBA66E A0A72865 DF77ECC4 6ADF2702
Round[3] After Sub Bytes
C1B9249F E05C344D 9EF5CE1C 029ECC77
Round[3] After Shift Rows
C15CCE77 E0F5CC9F 9E9E244D 02B9341C
Round[3] After Mix Columns
C4478324 8CC12C27 F7989F99 FC2BF7B3
Round[3] After Add Round Key
F9C7C459 CBD7D219 E9BBE1DD 91517F88
Round[4] After Sub Bytes
99C61CCB 1F0EB5D4 1EEAF8C1 81D1D2C4
Round[4] After Shift Rows
990EF8C4 1FEAD2CB 1ED11CD4 81C6B5C1
Round[4] After Mix Columns
07522BD5 02760C94 9C57905C 3C136E72
Round[4] After Add Round Key
E8168E94 AA2457EB 2A26B567 E718C372
Round[5] After Sub Bytes
9B471922 AC365BE9 E5F7D585 94AD2E40
Round[5] After Shift Rows
9B36D540 ACF72E22 E5AD19E9 94475B85
Round[5] After Mix Columns
E2D3DCD5 4D096172 CD665A49 2472F1AA
Round[5] After Add Round Key
36021A2D 318AFCF5 0794E2F5 358BE416
Round[6] After Sub Bytes
0577A2D8 C77EB0E6 C52298E6 963D6947
Round[6] After Shift Rows
057E9847 C72269D8 C53DA2E6 9677B0E6
Round[6] After Mix Columns
570D9967 42E044B2 92A4961C F855ABB1
Round[6] After Add Round Key
3A853A1D 53EB7A4F 495D105D 3255384C
Round[7] After Sub Bytes
809780A4 EDE9DA84 3B4CCA4C 23FC0729
Round[7] After Shift Rows
80E9CA29 ED4C07A4 3BFC8084 2397DA4C
Round[7] After Mix Columns
D8259DEA B6D85834 6DC74B22 722FCFB0
Round[7] After Add Round Key
96716AE4 E98791C7 E9610490 3C8913FF
Round[8] After Sub Bytes
90A30269 1E1781C6 1EEFF260 EBA77D16
Round[8] After Shift Rows
9017F216 1EEF7D69 1EA702C6 EBA38160
Round[8] After Mix Columns
E6A54262 0235B062 0A8BEC10 D24EF1C4
Round[8] After Add Round Key
0C773143 B7B80AB0 3BA01970 ADC3D8EB
Round[9] After Sub Bytes
FEF5C71A A96C67E7 E2E0D451 952E61E9
Round[9] After Shift Rows
FE6CD4E9 A9E0611A E22EC7E7 95F56751
Round[9] After Mix Columns
6EA80168 09CBA555 8D0B6B01 039C5D94
Round[9] After Add Round Key
C2DF679B 10317974 A5DA4240 54C05DFA
Round[10] After Sub Bytes
259E8514 CAC7B692 06572C09 20BA4C2D
Round[10] After Shift Rows
25C72C2D CA574C14 06BA8592 209EB609
Round[10] After Add Round Key
F5D3D585 03B9699D E785895A 96FDBAAF
Round[0] Input to Cipher
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[0] After Add Round Key
1BB60950 8BF236B7 4E0CD491 13C51DD3
Round[1] After Sub Bytes
AF4E0153 3D8905A9 2FFE4881 7DA6A466
Round[1] After Shift Rows
AF894866 3DFEA453 2FA601A9 7D4E0581
Round[1] After Mix Columns
EB181CE7 947E65BB 07D26B9F AC6FA1D5
Round[1] After Add Round Key
4BE2E2F0 1C2A490A 247152A6 8603D7D0
Round[2] After Sub Bytes
B398988C 9CE53B67 36A30024 447B0E70
Round[2] After Shift Rows
B3E50070 9CA30E8C 367B9867 44983B24
Round[2] After Mix Columns
3912C6CB 5F5FAC11 1E14CF77 2406C627
Round[2] After Add Round Key
CBD05339 25C91552 47214F0D 575F3058
Round[3] After Sub Bytes
1F70ED12 3FDD5900 A0FD84D7 5BCF046A
Round[3] After Shift Rows
1FDD846A 3FFD0412 A0CFED00 5B7059D7
Round[3] After Mix Columns
AC436FAC 74C0FC9C FC09AED9 A887FB71
Round[3] After Add Round Key
91C328D1 33D602A2 E22AD09D C5FD734A
Round[4] After Sub Bytes
812E343E C3F6773A 98E5705E A6548FD6
Round[4] After Shift Rows
81F670D6 C3E58F3E 9854343A A62E775E
Round[4] After Mix Columns
BE30F6A9 18A66148 D956EAA7 0C3D8414
Round[4] After Add Round Key
517453E8 B0F43A37 6F27CF9C D7362914
Round[5] After Sub Bytes
D192ED9B E7BF809A A8CC8ADE 0E05A5FA
Round[5] After Shift Rows
D1BF8AFA E7CCA59B A805ED9A 0E9280DE
Round[5] After Mix Columns
13CB74B2 A40BCC76 3314D924 EF74FEA7
Round[5] After Add Round Key
C71AB24A D88851F1 F9E66198 FE8DEB1B
Round[6] After Sub Bytes
C6A237D6 61C4D1A1 998EEF46 BB5DE9AF
Round[6] After Shift Rows
C6C4EFAF 618EE9D6 995D37A1 BBA2D146
Round[6] After Mix Columns
80D02D3F 74904773 58DB5283 07CA6A29
Round[6] After Add Round Key
ED588E45 659B798E 8322D4C2 CDCAF9D4
Round[7] After Sub Bytes
556A196E 4D14B619 EC934825 BD749948
Round[7] After Shift Rows
55144848 4D93996E EC741919 BD6AB625
Round[7] After Mix Columns
96ED0933 C3AE4501 5F368170 4C8DCF4A
Round[7] After Add Round Key
D8B9FE3D 9CF18CF2 DB90CEC2 022B1305
Round[8] After Sub Bytes
6156BB27 DEA16489 B9608B25 77F17D6B
Round[8] After Shift Rows
61A18B6B DE607D27 B9F1BB89 77566425
Round[8] After Mix Columns
DAD5705F 5DBE2D2A 531FA593 555286E1
Round[8] After Add Round Key
3007037E E83397F8 623450F3 2ADFAFCE
Round[9] After Sub Bytes
04C57BF3 9BC38841 AA18530D E59E798B
Round[9] After Shift Rows
04C3538B 9B1879F3 AA9E7B41 E5C5880D
Round[9] After Mix Columns
8EE7E791 8FD37F2A CC410182 00FA3C63
Round[9] After Add Round Key
22908162 9629A30B E49028C3 57A63C0D
Round[10] After Sub Bytes
93600CAA 90A50A2B 6960342E 5B24EBD7
Round[10] After Shift Rows
93A534D7 9060EBAA 69240C2B 5B600A2E
Round[10] After Add Round Key
43B1CD7F 598ECE23 881B00E3 ED030688
Round[0] Input to Cipher
F69F2445 DF4F9B17 AD2B417B E66C3710
Round[0] After Add Round Key
DDE13153 F7E149B1 06DC54F3 EFA3782C
Round[1] After Sub Bytes
C1F8C7ED 68F83BC8 6F86200D DF0ABC71
Round[1] After Shift Rows
C1F82071 6886BCED 6F0AC7C8 DFF83B0D
Round[1] After Mix Columns
DB3BEA62 104DA143 CFE1B3F7 807446A3
Round[1] After Add Round Key
7BC11475 98198DF2 EC428ACE AA1830A6
Round[2] After Sub Bytes
2178FA9D 46D45D89 CE2C7E8B ACAD0424
Round[2] After Shift Rows
21D47E24 462C049D CEADFA89 AC785D8B
Round[2] After Mix Columns
7F346581 618FDEC3 18130C17 1D30E8C7
Round[2] After Add Round Key
8DF6F073 1B196780 41268C6D 6E691EB8
Round[3] After Sub Bytes
5D428C8F AFD485CD 83F7643C 9FF9726C
Round[3] After Shift Rows
5DD4646C AFF7728F 83F98CCD 9F42853C
Round[3] After Mix Columns
D52EF58F BA43366A 4C28356A 5AB38805
Round[3] After Add Round Key
E8AEB2F2 FD55C854 520B4B2E 37C9003E
Round[4] After Sub Bytes
9BE43789 54FCE820 002BB331 9ADD63B2
Round[4] After Shift Rows
9BFCB3B2 542B6389 00DD3720 9AE4E831
Round[4] After Mix Columns
3304D786 3F2E39BD 6BD8D3AA C15BE6DB
Round[4] After Add Round Key
DC4072C7 977C62C2 DDA9F691 1A504BDB
Round[5] After Sub Bytes
860940C6 8810AA25 C1D34281 A253B3B9
Round[5] After Shift Rows
861042B9 88D3B3C6 C1534025 A209AA81
Round[5] After Mix Columns
DCD9C2AA 103D7774 09827D01 6FD47C47
Round[5] After Add Round Key
08080452 6CBEEAF3 C370C5BD 7E2D69FB
Round[6] After Sub Bytes
3030F200 50AE870D 2E51A67A F3D8F90F
Round[6] After Shift Rows
30AEA60F 5051F900 2ED8F20D F330877A
Round[6] After Mix Columns
2089D846 AAE2E858 D0851E42 507B584D
Round[6] After Add Round Key
4D017B3C BBE9D6A5 0B7C9803 9A7BCBB0
Round[7] After Sub Bytes
E37C21EB EA1EF606 2B10467B B8211FE7
Round[7] After Shift Rows
E31E46E7 EA101FEB 2B212106 B87CF67B
Round[7] After Mix Columns
5EF243B3 0B00E2E7 120C4271 623ABEAF
Round[7] After Add Round Key
10A6B4BD 545F2B14 96AA0DC3 2C9C62E0
Round[8] After Sub Bytes
CA248D7A 20CFF1FA 90ACD72E 71DEAAE1
Round[8] After Shift Rows
CACFD7E1 20ACAA7A 90DE8DFA 7124F12E
Round[8] After Mix Columns
F3CC8884 7FFC4D92 35415A17 511FDE1A
Round[8] After Add Round Key
191EFBA5 CA71F740 046AAF77 2E92F735
Round[9] After Sub Bytes
D4720F06 74A36809 F20279F5 314F6896
Round[9] After Shift Rows
D4A37996 74026806 F24F0F09 317268F5
Round[9] After Mix Columns
A294248A 80CEACFA 2874B85F 699897B8
Round[9] After Add Round Key
0EE34279 993470DB 00A5911E 3EC497D6
Round[10] After Sub Bytes
AB112CB6 EE1851B9 63068172 B21C88F6
Round[10] After Shift Rows
AB1881F6 EE0688B6 631C2CB9 B2115172
Round[10] After Add Round Key
7B0C785E 27E8AD3F 82232071 04725DD4
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
Enter option = 4
NIST Standard Test Data
128-Bit Cipher Key
2B7E1516 28AED2A6 ABF71588 09CF4F3C
Electronic Codebook (ECB) Mode
ECB-AES128 (Decryption)
NIST Standard Test Data
AES-128 (Nk = 4, Nr = 10)
Test Vectors
Round[10] Input to Inverse Cipher
3AD77BB4 0D7A3660 A89ECAF3 2466EF97
Round[10] After Add Round Key
EAC3821C C49413E9 49A1C63B 9205E331
Round[10] After Inverse Sub Bytes
BB3311C4 88E782EB A4F1C749 74364D2E
Round[10] After Inverse Shift Rows
BB36C7EB 88334D49 A4E7112E 74F182C4
Round[9] After Add RoundKey
1741A118 91C99168 8C36386F 23AD82AA
Round[9] After Mix Columns
8333F0AF FF15A6ED C191B409 770E815E
Round[9] After Inverse Sub Bytes
4166171B 7D2FC553 DDACC640 02D7919D
Round[9] After Inverse Shift Rows
41D7C653 7D669140 DD2F179D 02ACC51B
Round[8] After Add RoundKey
AB05B572 C8EB2B92 EC04E2FD 7D21EC34
Round[8] After Mix Columns
98B55410 09A9C5FF 1114EA18 7F3CFD3A
Round[8] After Inverse Sub Bytes
E2D2FD7C 40B7077D E39BBB34 6B6D21A2
Round[8] After Inverse Shift Rows
E26DBB7D 40D22134 E3B7FDA2 6B9B077C
Round[7] After Add RoundKey
AC394C73 1F8DE8C7 6711B210 253DDB33
Round[7] After Mix Columns
BD6D1268 F356657D DC66BAD4 F1E3F416
Round[7] After Inverse Sub Bytes
CDB339F7 7EB9BC13 93D3C019 2B4DBAFF
Round[7] After Inverse Shift Rows
CD4DC013 7EB3BA19 93B939FF 2BD3BCF7
Round[6] After Add RoundKey
A0C56369 6FB884E4 4840BFBE E1D32F0A
Round[6] After Mix Columns
712E6C5C 23D3BDFA E8310DDD 3FD6DF21
Round[6] After Inverse Sub Bytes
2CC3B8A7 32A9CD14 C82EF3C9 254AEF7B
Round[6] After Inverse Shift Rows
2C4AF314 32C3EFC9 C8A9B87B 252ECDA7
Round[5] After Add RoundKey
F89B35EC 4E40724E 025B00C7 34D7D81B
Round[5] After Mix Columns
3A06981E 1BA543CF BAA99F12 4FEFE363
Round[5] After Inverse Sub Bytes
A2A5E2E9 4429645F C0B76E39 92614D00
Round[5] After Inverse Shift Rows
A2616E5F 44A54D39 C029E200 92B764E9
Round[4] After Add RoundKey
4D25CB1E ECF71646 7658C73B 49BCC9E9
Round[4] After Mix Columns
912C7676 3AF956DE C0F2CE2E A93E98DA
Round[4] After Inverse Sub Bytes
AC420F0F A269B99C 1F04ECC3 B7D1E27A
Round[4] After Inverse Shift Rows
ACD1EC9C A242E2C3 1F690F7A B704B90F
Round[3] After Add RoundKey
9151ABE1 E5541CFD 014A713E DA7E3134
Round[3] After Mix Columns
54FE6141 B3B0EAB9 68D310AF D60D641E
Round[3] After Inverse Sub Bytes
FD0CD8F8 4BFCBBDB F7A97C1B 4AF38CE9
Round[3] After Inverse Shift Rows
FDF37CDB 4B0C8C1B F7FCD8E9 4AA9BBF8
Round[2] After Add RoundKey
0F31E929 319A3558 AEC95893 39F04D87
Round[2] After Mix Columns
89B5884A C0565303 2E389B21 604D123C
Round[2] After Inverse Sub Bytes
F2D2975C 1FB950D5 C376E87B 9065396D
Round[2] After Inverse Shift Rows
F265E8D5 1FD2397B C3B9976D 9076505C
Round[1] After Add RoundKey
529F16C2 978615CA E01AAE54 BA1A2659
Round[1] After Mix Columns
09287F47 6F746ABF 2C4A6204 DA08E3EE
Round[1] After Inverse Sub Bytes
40EE6B16 06CA58F4 425CAB30 7ABF4D99
Round[1] After Inverse Shift Rows
40BFABF4 06EE4D30 42CA6B99 7A5C5816
Round[0] After Add Round Key
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[10] Input to Inverse Cipher
F5D3D585 03B9699D E785895A 96FDBAAF
Round[10] After Add Round Key
25C72C2D CA574C14 06BA8592 209EB609
Round[10] After Inverse Sub Bytes
C23142FA 10DA5D9B A5C06774 54DF7940
Round[10] After Inverse Shift Rows
C2DF679B 10317974 A5DA4240 54C05DFA
Round[9] After Add RoundKey
6EA80168 09CBA555 8D0B6B01 039C5D94
Round[9] After Mix Columns
FE6CD4E9 A9E0611A E22EC7E7 95F56751
Round[9] After Inverse Sub Bytes
0CB819EB B7A0D843 3BC331B0 AD770A70
Round[9] After Inverse Shift Rows
0C773143 B7B80AB0 3BA01970 ADC3D8EB
Round[8] After Add RoundKey
E6A54262 0235B062 0A8BEC10 D24EF1C4
Round[8] After Mix Columns
9017F216 1EEF7D69 1EA702C6 EBA38160
Round[8] After Inverse Sub Bytes
968704FF E96113E4 E9896AC7 3C719190
Round[8] After Inverse Shift Rows
96716AE4 E98791C7 E9610490 3C8913FF
Round[7] After Add RoundKey
D8259DEA B6D85834 6DC74B22 722FCFB0
Round[7] After Mix Columns
80E9CA29 ED4C07A4 3BFC8084 2397DA4C
Round[7] After Inverse Sub Bytes
3AEB104C 535D381D 49553A4F 32857A5D
Round[7] After Inverse Shift Rows
3A853A1D 53EB7A4F 495D105D 3255384C
Round[6] After Add RoundKey
570D9967 42E044B2 92A4961C F855ABB1
Round[6] After Mix Columns
057E9847 C72269D8 C53DA2E6 9677B0E6
Round[6] After Inverse Sub Bytes
368AE216 3194E42D 078B1AF5 3502FCF5
Round[6] After Inverse Shift Rows
36021A2D 318AFCF5 0794E2F5 358BE416
Round[5] After Add RoundKey
E2D3DCD5 4D096172 CD665A49 2472F1AA
Round[5] After Mix Columns
9B36D540 ACF72E22 E5AD19E9 94475B85
Round[5] After Inverse Sub Bytes
E824B572 AA26C394 2A188EEB E7165767
Round[5] After Inverse Shift Rows
E8168E94 AA2457EB 2A26B567 E718C372
Round[4] After Add RoundKey
07522BD5 02760C94 9C57905C 3C136E72
Round[4] After Mix Columns
990EF8C4 1FEAD2CB 1ED11CD4 81C6B5C1
Round[4] After Inverse Sub Bytes
F9D7E188 CBBB7F59 E951C419 91C7D2DD
Round[4] After Inverse Shift Rows
F9C7C459 CBD7D219 E9BBE1DD 91517F88
Round[3] After Add RoundKey
C4478324 8CC12C27 F7989F99 FC2BF7B3
Round[3] After Mix Columns
C15CCE77 E0F5CC9F 9E9E244D 02B9341C
Round[3] After Inverse Sub Bytes
DDA7EC02 A077276E DFDFA665 6ADB28C4
Round[3] After Inverse Shift Rows
DDDBA66E A0A72865 DF77ECC4 6ADF2702
Round[2] After Add RoundKey
2F19339C DA319126 86426CBE 1986D17D
Round[2] After Mix Columns
0E523BFE AABC5913 3665F0B5 81592FC4
Round[2] After Inverse Sub Bytes
D748490C 62781582 24BC17D2 91154E88
Round[2] After Inverse Shift Rows
D7151782 62484ED2 24784988 91BC150C
Round[1] After Add RoundKey
77EFE995 EA1C6263 07DB70B1 BBD06309
Round[1] After Mix Columns
9795DA3C 05097883 96D0DB80 29EDF336
Round[1] After Inverse Sub Bytes
85AD7A6D 3640C141 35609F3A 4C537E24
Round[1] After Inverse Shift Rows
85539F41 36AD7E3A 35407A24 4C60C16D
Round[0] After Add Round Key
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[10] Input to Inverse Cipher
43B1CD7F 598ECE23 881B00E3 ED030688
Round[10] After Add Round Key
93A534D7 9060EBAA 69240C2B 5B600A2E
Round[10] After Inverse Sub Bytes
2229280D 96903C62 E4A6810B 5790A3C3
Round[10] After Inverse Shift Rows
22908162 9629A30B E49028C3 57A63C0D
Round[9] After Add RoundKey
8EE7E791 8FD37F2A CC410182 00FA3C63
Round[9] After Mix Columns
04C3538B 9B1879F3 AA9E7B41 E5C5880D
Round[9] After Inverse Sub Bytes
303350CE E834AF7E 62DF03F8 2A0797F3
Round[9] After Inverse Shift Rows
3007037E E83397F8 623450F3 2ADFAFCE
Round[8] After Add RoundKey
DAD5705F 5DBE2D2A 531FA593 555286E1
Round[8] After Mix Columns
61A18B6B DE607D27 B9F1BB89 77566425
Round[8] After Inverse Sub Bytes
D8F1CE05 9C90133D DB2BFEF2 02B98CC2
Round[8] After Inverse Shift Rows
D8B9FE3D 9CF18CF2 DB90CEC2 022B1305
Round[7] After Add RoundKey
96ED0933 C3AE4501 5F368170 4C8DCF4A
Round[7] After Mix Columns
55144848 4D93996E EC741919 BD6AB625
Round[7] After Inverse Sub Bytes
ED9BD4D4 6522F945 83CA8E8E CD5879C2
Round[7] After Inverse Shift Rows
ED588E45 659B798E 8322D4C2 CDCAF9D4
Round[6] After Add RoundKey
80D02D3F 74904773 58DB5283 07CA6A29
Round[6] After Mix Columns
C6C4EFAF 618EE9D6 995D37A1 BBA2D146
Round[6] After Inverse Sub Bytes
C788611B D8E6EB4A F98DB2F1 FE1A5198
Round[6] After Inverse Shift Rows
C71AB24A D88851F1 F9E66198 FE8DEB1B
Round[5] After Add RoundKey
13CB74B2 A40BCC76 3314D924 EF74FEA7
Round[5] After Mix Columns
D1BF8AFA E7CCA59B A805ED9A 0E9280DE
Round[5] After Inverse Sub Bytes
51F4CF14 B02729E8 6F365337 D7743A9C
Round[5] After Inverse Shift Rows
517453E8 B0F43A37 6F27CF9C D7362914
Round[4] After Add RoundKey
BE30F6A9 18A66148 D956EAA7 0C3D8414
Round[4] After Mix Columns
81F670D6 C3E58F3E 9854343A A62E775E
Round[4] After Inverse Sub Bytes
91D6D04A 332A73D1 E2FD28A2 C5C3029D
Round[4] After Inverse Shift Rows
91C328D1 33D602A2 E22AD09D C5FD734A
Round[3] After Add RoundKey
AC436FAC 74C0FC9C FC09AED9 A887FB71
Round[3] After Mix Columns
1FDD846A 3FFD0412 A0CFED00 5B7059D7
Round[3] After Inverse Sub Bytes
CBC94F58 25213039 475F5352 57D0150D
Round[3] After Inverse Shift Rows
CBD05339 25C91552 47214F0D 575F3058
Round[2] After Add RoundKey
3912C6CB 5F5FAC11 1E14CF77 2406C627
Round[2] After Mix Columns
B3E50070 9CA30E8C 367B9867 44983B24
Round[2] After Inverse Sub Bytes
4B2A52D0 1C71D7F0 2403E20A 86E249A6
Round[2] After Inverse Shift Rows
4BE2E2F0 1C2A490A 247152A6 8603D7D0
Round[1] After Add RoundKey
EB181CE7 947E65BB 07D26B9F AC6FA1D5
Round[1] After Mix Columns
AF894866 3DFEA453 2FA601A9 7D4E0581
Round[1] After Inverse Sub Bytes
1BF2D4D3 8B0C1D50 4EC509B7 13B63691
Round[1] After Inverse Shift Rows
1BB60950 8BF236B7 4E0CD491 13C51DD3
Round[0] After Add Round Key
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[10] Input to Inverse Cipher
7B0C785E 27E8AD3F 82232071 04725DD4
Round[10] After Add Round Key
AB1881F6 EE0688B6 631C2CB9 B2115172
Round[10] After Inverse Sub Bytes
0E3491D6 99A59779 00C442DB 3EE3701E
Round[10] After Inverse Shift Rows
0EE34279 993470DB 00A5911E 3EC497D6
Round[9] After Add RoundKey
A294248A 80CEACFA 2874B85F 699897B8
Round[9] After Mix Columns
D4A37996 74026806 F24F0F09 317268F5
Round[9] After Inverse Sub Bytes
1971AF35 CA6AF7A5 0492FB40 2E1EF777
Round[9] After Inverse Shift Rows
191EFBA5 CA71F740 046AAF77 2E92F735
Round[8] After Add RoundKey
F3CC8884 7FFC4D92 35415A17 511FDE1A
Round[8] After Mix Columns
CACFD7E1 20ACAA7A 90DE8DFA 7124F12E
Round[8] After Inverse Sub Bytes
105F0DE0 54AA62BD 969CB414 2CA62BC3
Round[8] After Inverse Shift Rows
10A6B4BD 545F2B14 96AA0DC3 2C9C62E0
Round[7] After Add RoundKey
5EF243B3 0B00E2E7 120C4271 623ABEAF
Round[7] After Mix Columns
E31E46E7 EA101FEB 2B212106 B87CF67B
Round[7] After Inverse Sub Bytes
4DE998B0 BB7CCB3C 0B7B7BA5 9A01D603
Round[7] After Inverse Shift Rows
4D017B3C BBE9D6A5 0B7C9803 9A7BCBB0
Round[6] After Add RoundKey
2089D846 AAE2E858 D0851E42 507B584D
Round[6] After Mix Columns
30AEA60F 5051F900 2ED8F20D F330877A
Round[6] After Inverse Sub Bytes
08BEC5FB 6C706952 C32D04F3 7E08EABD
Round[6] After Inverse Shift Rows
08080452 6CBEEAF3 C370C5BD 7E2D69FB
Round[5] After Add RoundKey
DCD9C2AA 103D7774 09827D01 6FD47C47
Round[5] After Mix Columns
861042B9 88D3B3C6 C1534025 A209AA81
Round[5] After Inverse Sub Bytes
DC7CF6DB 97A94BC7 DD5072C2 1A406291
Round[5] After Inverse Shift Rows
DC4072C7 977C62C2 DDA9F691 1A504BDB
Round[4] After Add RoundKey
3304D786 3F2E39BD 6BD8D3AA C15BE6DB
Round[4] After Mix Columns
9BFCB3B2 542B6389 00DD3720 9AE4E831
Round[4] After Inverse Sub Bytes
E8554B3E FD0B00F2 52C9B254 37AEC82E
Round[4] After Inverse Shift Rows
E8AEB2F2 FD55C854 520B4B2E 37C9003E
Round[3] After Add RoundKey
D52EF58F BA43366A 4C28356A 5AB38805
Round[3] After Mix Columns
5DD4646C AFF7728F 83F98CCD 9F42853C
Round[3] After Inverse Sub Bytes
8D198CB8 1B261E73 4169F080 6EF6676D
Round[3] After Inverse Shift Rows
8DF6F073 1B196780 41268C6D 6E691EB8
Round[2] After Add RoundKey
7F346581 618FDEC3 18130C17 1D30E8C7
Round[2] After Mix Columns
21D47E24 462C049D CEADFA89 AC785D8B
Round[2] After Inverse Sub Bytes
7B198AA6 98423075 EC1814F2 AAC18DCE
Round[2] After Inverse Shift Rows
7BC11475 98198DF2 EC428ACE AA1830A6
Round[1] After Add RoundKey
DB3BEA62 104DA143 CFE1B3F7 807446A3
Round[1] After Mix Columns
C1F82071 6886BCED 6F0AC7C8 DFF83B0D
Round[1] After Inverse Sub Bytes
DDE1542C F7DC7853 06A331B1 EFE149F3
Round[1] After Inverse Shift Rows
DDE13153 F7E149B1 06DC54F3 EFA3782C
Round[0] After Add Round Key
F69F2445 DF4F9B17 AD2B417B E66C3710
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
Enter option = 5
NIST Standard Test Data
192-Bit Cipher Key
8E73B0F7 DA0E6452 C810F32B 809079E5 62F8EAD2 522C6B7B
Electronic Codebook (ECB) Mode
ECB-AES192 (Encryption)
NIST Standard Test Data
AES-192 (Nk = 6, Nr = 12)
Test Vectors
Round[0] Input to Cipher
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[0] After Add Round Key
E5B20E15 F44EFBC4 212D8D3A F3036ECF
Round[1] After Sub Bytes
D937AB59 BF2F0F1C FDD85D80 0D7B9F8A
Round[1] After Shift Rows
D92F5D8A BFD89F59 FD7BAB1C 0D370F80
Round[1] After Mix Columns
0FEAC90D D0F7A92F DBF1EFF4 CCF2BF34
Round[1] After Add Round Key
6D1223DF 82DBC254 25FD7E03 E8F04A91
Round[2] After Sub Bytes
3CC9269E 13B92520 3F54F37B 9B8CD681
Round[2] After Shift Rows
3CB9F381 1354D69E 3F8C2620 9BC9257B
Round[2] After Mix Columns
DADAE017 92444990 F7769FAB 330695AC
Round[2] After Add Round Key
36C8E699 FEC636FB F90C0A12 6F506B6E
Round[3] After Sub Bytes
05E88EEE BBB4050F 99FE67C9 A8537F9F
Round[3] After Shift Rows
05B4679F BBFE7FEE 99538E0F A8E805C9
Round[3] After Mix Columns
3540C5F9 E5339290 5DB9DC73 A4A50A87
Round[3] After Add Round Key
78F77144 8C86D388 D81E9BE5 4D80327A
Round[4] After Sub Bytes
BC68A31B 644466C4 617214D9 E3CD23DA
Round[4] After Shift Rows
BC4414DA 6472231B 61CDA3C4 E36866D9
Round[4] After Mix Columns
61D2A520 66FE7DCB E9DAA65E DA403799
Round[4] After Add Round Key
868D0864 DDF72E4D A1805609 FBAF86D6
Round[5] After Sub Bytes
445D3043 C16831E3 32CDB101 0F7944F6
Round[5] After Shift Rows
4468B1F6 C1CD4443 327930E3 0F5D3101
Round[5] After Mix Columns
77AA54E2 D2CF4157 3C7315C2 C9E7337F
Round[5] After Add Round Key
D3E2A23B 9FA28F73 964176A2 D8DC0399
Round[6] After Sub Bytes
66983AE2 DB3A738F 9083383A 61867BEE
Round[6] After Shift Rows
663A38EE DB837BE2 90863A8F 6198733A
Round[6] After Mix Columns
54B4056F AAA99351 1F46E812 38E5513C
Round[6] After Add Round Key
F6EA7BBA 29185CCB 38BFD151 5271A65B
Round[7] After Sub Bytes
428721F4 A5AD4A1F 07083ED1 00A32439
Round[7] After Shift Rows
42AD3E39 A50824F4 07A3211F 00874AD1
Round[7] After Mix Columns
6F78D827 992DE22B CE26C7B5 091A7B74
Round[7] After Add Round Key
AFDE4C20 48B046CA 2231415E 66BC3205
Round[8] After Sub Bytes
791D29B7 52E75A74 93C78358 3365236B
Round[8] After Shift Rows
79E7836B 52C723B7 93652974 331D5A58
Round[8] After Mix Columns
28593E39 62151167 CF56380A 43BF72A2
Round[8] After Add Round Key
60064E0B 40DE9632 2D3B2B58 704FC511
Round[9] After Sub Bytes
D06F2F2B 091D9023 D8E2F16A 5184A682
Round[9] After Shift Rows
D01DF182 09E2A62B D8842F23 516F906A
Round[9] After Mix Columns
EF60A998 A20CC109 3099679E E94EBBD8
Round[9] After Add Round Key
AFDE42B0 8D146350 57DEB5F5 ACC2EEE6
Round[10] After Sub Bytes
791D2CE7 5DFAFB53 5B1DD5E6 9125288E
Round[10] After Shift Rows
79FAD58E 5D1D28E7 5B252C53 911DFBE6
Round[10] After Mix Columns
BC7CBBA3 52F82207 A636D342 035B5099
Round[10] After Add Round Key
1B9DFDCF C6E9D3D8 2429A648 AE5C87CA
Round[11] After Sub Bytes
AF5E548A B41E6661 36A52452 E44A1774
Round[11] After Shift Rows
AF1E2474 B4A5178A 364A5461 E45E6652
Round[11] After Mix Columns
378B6538 1A56BA7A 873F7786 05A080AB
Round[11] After Add Round Key
FDCB6000 959AEA7C AF1261EC B99C671E
Round[12] After Sub Bytes
541FD063 2AB88710 79C9EFCE 56DE8572
Round[12] After Shift Rows
54B8EF72 2AC98563 79DED010 561F87CE
Round[12] After Add Round Key
BD334F1D 6E45F25F F712A214 571FA5CC
Round[0] Input to Cipher
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[0] After Add Round Key
205E3AA0 C40DC8CE 56A79C87 C53FF7B4
Round[1] After Sub Bytes
B75880E0 1CD7E88B B15CDE17 A675688D
Round[1] After Shift Rows
B7D7DE8D 1C5C68E0 B175808B A658E817
Round[1] After Mix Columns
44F64BCA 54FCABCB ED4B5930 40220C6F
Round[1] After Add Round Key
260EA118 06D0C0B0 1347C8C7 6420F9CA
Round[2] After Sub Bytes
F7AB32AD 6F70BAE7 7DA0E8C6 43B79974
Round[2] After Shift Rows
F770E874 6FA099AD 7DB732E7 43ABBAC6
Round[2] After Mix Columns
F940D072 11290AC9 EDB99CD7 1C1DD643
Round[2] After Add Round Key
1552D6FC 7DAB75A2 E3C3096E 404B2881
Round[3] After Sub Bytes
5900F6B0 FF629D3A 112E019F 09B3340C
Round[3] After Shift Rows
5962010C FF2E34B0 11B3F63A 09009D9F
Round[3] After Mix Columns
19922D90 134F727B 20571B02 102A92A3
Round[3] After Add Round Key
5425992D 7AFA3363 A5F05C94 F90FAA5E
Round[4] After Sub Bytes
203FEED8 DA2DC3FB 068C4A22 9976AC58
Round[4] After Shift Rows
202D4A58 DA8CACD8 0676EEFB 993FC322
Round[4] After Mix Columns
25FC71B7 54EE66FE 8338A17F 899B5D08
Round[4] After Add Round Key
C2A3DCF3 EFE73578 CB625128 A874EC47
Round[5] After Sub Bytes
250A860D DF9496BC 1FAAD134 C292CEA0
Round[5] After Shift Rows
2594D1A0 DFAACE0D 1F9286BC C20A9634
Round[5] After Mix Columns
9CDEF371 83D4E504 A90D4556 2343A3A9
Round[5] After Add Round Key
389605A8 CEB92B20 033F2636 3278934F
Round[6] After Sub Bytes
07906BC2 8B56F1B7 7B75F705 23BCDC84
Round[6] After Shift Rows
0756F784 8B75DCC2 7BBC6BB7 2390F105
Round[6] After Mix Columns
872D33BB 8CDC00B0 F512D32F 1915450E
Round[6] After Add Round Key
25734D6E 0F6DCF2A D2EBEA6C 7381B269
Round[7] After Sub Bytes
3F8FE39F 763C8AE5 B5E98750 8F0C37F9
Round[7] After Shift Rows
3F3C87F9 76E9379F B50CE3E5 8F8F8A50
Round[7] After Mix Columns
442C0613 64794B61 637650FA 555FFF2F
Round[7] After Add Round Key
848A9214 B5E4EF80 8F61D611 3AF9B65E
Round[8] After Sub Bytes
5F7E4FFA D569DFCD 73EFF682 80994E58
Round[8] After Shift Rows
5F69F658 D5EF4EFA 73994FCD 807EDF82
Round[8] After Mix Columns
ABD429CE 2F38B32A D44638C2 C484C625
Round[8] After Add Round Key
E38B59FC 0DF3347F 362B2B90 F7747196
Round[9] After Sub Bytes
113DCBB0 D70D18D2 05F1F160 6892A390
Round[9] After Shift Rows
110DF190 D7F1A3B0 0592CBD2 683D1860
Round[9] After Mix Columns
54934EF4 AE60B04B BEAE77E9 EF5AC55D
Round[9] After Add Round Key
142DA5DC 81781212 D9E9A582 AAD69063
Round[10] After Sub Bytes
FAD80686 0CBCC9C9 351E0613 ACF660FB
Round[10] After Shift Rows
FABC06FB 0C1E6086 35F606C9 ACD8C913
Round[10] After Mix Columns
CD685C42 DC16437D A4018F26 EA54C8D8
Round[10] After Add Round Key
6A891A2E 4807B2A2 261EFA2C 47531F8B
Round[11] After Sub Bytes
02A7A231 52C5373A F7722D71 A0EDC03D
Round[11] After Shift Rows
02C52D3D 5272C031 F7EDA23A A0A73771
Round[11] After Mix Columns
40D9DA94 C3DCE826 41F10B39 EFDDFA89
Round[11] After Add Round Key
8A99DFAC 4C10B820 69DC1D53 53E11D3C
Round[12] After Sub Bytes
7EEE9E91 29CA6CB7 F986A4ED EDF8A4EB
Round[12] After Shift Rows
7ECAA4EB 2986A491 F9F89EB7 EDEE6CED
Round[12] After Add Round Key
97410484 6D0AD3AD 7734ECB3 ECEE4EEF
Round[0] Input to Cipher
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[0] After Add Round Key
BEBBACB1 79528043 2DEB3232 9A9A2B0A
Round[1] After Sub Bytes
AEEA91C8 B600CD1A D8E92323 B8B8F167
Round[1] After Shift Rows
AE002367 B6E9F1C8 D8B8911A B8EACD23
Round[1] After Mix Columns
03AC4104 6EBFE552 F301776E A018B6B2
Round[1] After Add Round Key
6154ABD6 3C938E29 0D0DE699 841A4317
Round[2] After Sub Bytes
EF2062F6 EBDC19A5 D7D78EEE 5FA21AF0
Round[2] After Shift Rows
EFDC8EF0 EBD71AF6 D7A262A5 5F2019EE
Round[2] After Mix Columns
C4353F83 4386091C 8F8B45F3 29DA641F
Round[2] After Add Round Key
2827390D 2F047677 81F1D04A 758C9ADD
Round[3] After Sub Bytes
34CC12D7 15F238F5 0CA170D6 9D64B8C1
Round[3] After Shift Rows
34F270C1 15A1B8D7 0C6412F5 9DCC38D6
Round[3] After Mix Columns
D49A7E47 BD48BD93 53074893 808040FF
Round[3] After Add Round Key
992DCAFA D4FDFC8B D6A00F05 69A57802
Round[4] After Sub Bytes
EED8742D 4854B03D F6E0766B F906BC77
Round[4] After Shift Rows
EE547677 48E0BC2D F606743D F9D8B06B
Round[4] After Mix Columns
3AABCFE5 3A61BCDE B45B5F09 41F2E7AE
Round[4] After Add Round Key
DDF462A1 8168EF58 FC01AF5E 601D56E1
Round[5] After Sub Bytes
C1BFAA32 0C45DF6A B07C7958 D0A4B1F8
Round[5] After Shift Rows
C14579F8 0C7CB132 B0A4AA6A D0BFDF58
Round[5] After Mix Columns
D738658F 1F0E5FBD 4C6CE511 E69722BB
Round[5] After Add Round Key
73709356 52639199 E65E8671 F7AC125D
Round[6] After Sub Bytes
8F51DCB1 00FB81EE 8E5844A3 6891C94C
Round[6] After Shift Rows
8FFB444C 0058C9B1 8E91DCEE 685181A3
Round[6] After Mix Columns
1BE228AD 904119E8 9D269503 01F1DE35
Round[6] After Add Round Key
B9BC5678 13F0D672 BADFAC40 6B652952
Round[7] After Sub Bytes
5665B1BC 7D8CF640 F49E9109 7F4DA500
Round[7] After Shift Rows
568C9100 7D9EA5BC F44DB140 7F65F609
Round[7] After Mix Columns
B2FDE3E7 5A126DDF D5E6007B AEBDF600
Round[7] After Add Round Key
725B77E0 8B8FC93E 39F18690 C11BBF71
Round[8] After Sub Bytes
4039F5E1 3D73DDB2 12A14460 78AF08A3
Round[8] After Shift Rows
407344A3 3DA108E1 12AFF5B2 7839DD60
Round[8] After Mix Columns
F2C945AA 6B9DB437 89E18113 061640AC
Round[8] After Add Round Key
BA963598 49563362 6B8C9241 35E6F71F
Round[9] After Sub Bytes
F4909646 3BB1C3AA 7F644F83 968E68C0
Round[9] After Shift Rows
F4B14FC0 3B646846 7F8E96AA 9690C383
Round[9] After Mix Columns
B49C8062 F40D45CD 4B7323D6 DC7005EF
Round[9] After Add Round Key
F4226B4A DB15E794 2C34F1BD 99FC50D1
Round[10] After Sub Bytes
BF937FD6 B9599422 7118A17A EEB0533E
Round[10] After Shift Rows
BF59A13E B91853D6 71B07F22 EE93947A
Round[10] After Mix Columns
11CBFD5E C4AA662C 74A95918 870EC0DA
Round[10] After Add Round Key
B62ABB32 50BB97F3 F6B62C12 2A091789
Round[11] After Sub Bytes
4EE5EA23 53EA880D 424E71C9 E501F0A7
Round[11] After Shift Rows
4EEA71A7 534EF023 4201EA0D E5E588C9
Round[11] After Mix Columns
6FB5B41C A7E7830D 60689B37 A47E4BD0
Round[11] After Add Round Key
A5F5B124 282BD30B 48458D5D 1842AC65
Round[12] After Sub Bytes
06E6C836 34F1662B 526E5D4C AD2C914D
Round[12] After Shift Rows
06F15D4D 346E9136 522CC82B ADE6664C
Round[12] After Add Round Key
EF7AFD22 70E2E60A DCE0BA2F ACE6444E
Round[0] Input to Cipher
F69F2445 DF4F9B17 AD2B417B E66C3710
Round[0] After Add Round Key
78EC94B2 0541FF45 653BB250 66FC4EF5
Round[1] After Sub Bytes
BCCE2237 6B83166E 4DE23753 33B02FE6
Round[1] After Shift Rows
BC8337E6 6BE22F37 4DB0226E 33CE1653
Round[1] After Mix Columns
2C1E60BC F3F28E1E 1D3E0B99 6ADD242B
Round[1] After Add Round Key
4EE68A6E A1DEE565 E3329A6E 4EDFD18E
Round[2] After Sub Bytes
2F8E7E9F 321DD94D 1123B89F 2F9E3E19
Round[2] After Shift Rows
2F1DB819 32233E9F 119E7E4D 2F8ED99F
Round[2] After Mix Columns
D8DF72E6 A0A9D76E A8F9A449 91C7B203
Round[2] After Add Round Key
34CD7468 CC2BA805 A68331F0 CD914CC1
Round[3] After Sub Bytes
18BD9245 4BF1C26B 24ECC78C BD812978
Round[3] After Shift Rows
18F1C778 4BEC2945 2481926B BDBDC28C
Round[3] After Mix Columns
87CBF4EE D5B63A92 29FB27A9 F30D10A0
Round[3] After Add Round Key
CA7C4053 BC037B8A AC5C603F 1A28285D
Round[4] After Sub Bytes
741009ED 657B217E 914AD075 A234344C
Round[4] After Shift Rows
747BD04C 654A34ED 9134097E A2102175
Round[4] After Mix Columns
F9A560AF CD406B10 129C3569 3B946F26
Round[4] After Add Round Key
1EFACDEB 76493896 5AC6C53E 1A7BDE69
Round[5] After Sub Bytes
722DBDE9 383B0790 BEB4A6B2 A2211DF9
Round[5] After Shift Rows
723BA6F9 38B41DE9 BE21BD90 A22D07B2
Round[5] After Mix Columns
F60C0EE2 43859628 29B0557E 9D434CA8
Round[5] After Add Round Key
5244F83B 0EE8580C 8382361E 8C787C4E
Round[6] After Sub Bytes
001B41E2 AB9B6AFE EC130572 64BC102F
Round[6] After Shift Rows
009B052F AB1310E2 ECBC41FE 641B6A72
Round[6] After Mix Columns
9C0DE0C0 8A5FA53A A3B2CB35 FD9E3D39
Round[6] After Add Round Key
3E539E15 09EE6AA0 844BF276 970ACA5E
Round[7] After Sub Bytes
B2ED0B59 012802E0 5FB38938 88677458
Round[7] After Shift Rows
B2288958 01B37459 5F670BE0 88ED0238
Round[7] After Mix Columns
D63A7BDC E1B9B176 FC6C1556 1D77291C
Round[7] After Add Round Key
169CEFDB 30241597 107B93BD 72D1606D
Round[8] After Sub Bytes
47DEDFB9 04365988 CA21DC7A 403ED03C
Round[8] After Shift Rows
4736DC3C 0421D0B9 CA3EDF88 40DE597A
Round[8] After Mix Columns
3468965B 02944E94 9A44D2AF DA76A2B3
Round[8] After Add Round Key
7C37E669 205FC9C1 7829C1FD E9861500
Round[9] After Sub Bytes
109A8EF9 B7CFDD78 BCA57854 1E445963
Round[9] After Shift Rows
10CF7863 B7A559F9 BC448E78 1E9ADD54
Round[9] After Mix Columns
717E8A41 21F4B0D7 59C577E5 0019D9CD
Round[9] After Add Round Key
31C06169 0EEC128E 3E82A58E 45958CF3
Round[10] After Sub Bytes
C7BAEFF9 ABCEC919 B2130619 6E2A640D
Round[10] After Shift Rows
C7CE060D AB1364F9 B22AEF19 6EBAC919
Round[10] After Mix Columns
D7471280 E5D86078 F7D5763A D95876F3
Round[10] After Add Round Key
70A654EC 71C991A7 75CA0330 745FA1A0
Round[11] After Sub Bytes
512420CE A3DD815C 9D747B04 92CF32E0
Round[11] After Shift Rows
51DD7BE0 A37432CE 9DCF205C 92248104
Round[11] After Mix Columns
459D418E 3DD3FA3F 1724F6EB D646A300
Round[11] After Add Round Key
8FDD44B6 B21FAA39 3F09E081 6A7A44B5
Round[12] After Sub Bytes
73C11B4E 37C0AC12 7501E10C 02DA1BD5
Round[12] After Shift Rows
73C0E1D5 37011B4E 75DA1B12 02C1AC0C
Round[12] After Add Round Key
9A4B41BA 738D6C72 FB166916 03C18E0E
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
Enter option = 6
NIST Standard Test Data
192-Bit Cipher Key
8E73B0F7 DA0E6452 C810F32B 809079E5 62F8EAD2 522C6B7B
Electronic Codebook (ECB) Mode
ECB-AES192 (Decryption)
NIST Standard Test Data
AES-192 (Nk = 6, Nr = 12)
Test Vectors
Round[12] Input to Inverse Cipher
BD334F1D 6E45F25F F712A214 571FA5CC
Round[12] After Add Round Key
54B8EF72 2AC98563 79DED010 561F87CE
Round[12] After Inverse Sub Bytes
FD9A611E 95126700 AF9C607C B9CBEAEC
Round[12] After Inverse Shift Rows
FDCB6000 959AEA7C AF1261EC B99C671E
Round[11] After Add RoundKey
378B6538 1A56BA7A 873F7786 05A080AB
Round[11] After Mix Columns
AF1E2474 B4A5178A 364A5461 E45E6652
Round[11] After Inverse Sub Bytes
1BE9A6CA C62987CF 245CFDD8 AE9DD348
Round[11] After Inverse Shift Rows
1B9DFDCF C6E9D3D8 2429A648 AE5C87CA
Round[10] After Add RoundKey
BC7CBBA3 52F82207 A636D342 035B5099
Round[10] After Mix Columns
79FAD58E 5D1D28E7 5B252C53 911DFBE6
Round[10] After Inverse Sub Bytes
AF14B5E6 8DDEEEB0 57C24250 ACDE63F5
Round[10] After Inverse Shift Rows
AFDE42B0 8D146350 57DEB5F5 ACC2EEE6
Round[9] After Add RoundKey
EF60A998 A20CC109 3099679E E94EBBD8
Round[9] After Mix Columns
D01DF182 09E2A62B D8842F23 516F906A
Round[9] After Inverse Sub Bytes
60DE2B11 403BC50B 2D4F4E32 70069658
Round[9] After Inverse Shift Rows
60064E0B 40DE9632 2D3B2B58 704FC511
Round[8] After Add RoundKey
28593E39 62151167 CF56380A 43BF72A2
Round[8] After Mix Columns
79E7836B 52C723B7 93652974 331D5A58
Round[8] After Inverse Sub Bytes
AFB04105 48313220 22BC4CCA 66DE465E
Round[8] After Inverse Shift Rows
AFDE4C20 48B046CA 2231415E 66BC3205
Round[7] After Add RoundKey
6F78D827 992DE22B CE26C7B5 091A7B74
Round[7] After Mix Columns
42AD3E39 A50824F4 07A3211F 00874AD1
Round[7] After Inverse Sub Bytes
F618D15B 29BFA6BA 38717BCB 52EA5C51
Round[7] After Inverse Shift Rows
F6EA7BBA 29185CCB 38BFD151 5271A65B
Round[6] After Add RoundKey
54B4056F AAA99351 1F46E812 38E5513C
Round[6] After Mix Columns
663A38EE DB837BE2 90863A8F 6198733A
Round[6] After Inverse Sub Bytes
D3A27699 9F41033B 96DCA273 D8E28FA2
Round[6] After Inverse Shift Rows
D3E2A23B 9FA28F73 964176A2 D8DC0399
Round[5] After Add RoundKey
77AA54E2 D2CF4157 3C7315C2 C9E7337F
Round[5] After Mix Columns
4468B1F6 C1CD4443 327930E3 0F5D3101
Round[5] After Inverse Sub Bytes
86F756D6 DD808664 A1AF084D FB8D2E09
Round[5] After Inverse Shift Rows
868D0864 DDF72E4D A1805609 FBAF86D6
Round[4] After Add RoundKey
61D2A520 66FE7DCB E9DAA65E DA403799
Round[4] After Mix Columns
BC4414DA 6472231B 61CDA3C4 E36866D9
Round[4] After Inverse Sub Bytes
78869B7A 8C1E3244 D8807188 4DF7D3E5
Round[4] After Inverse Shift Rows
78F77144 8C86D388 D81E9BE5 4D80327A
Round[3] After Add RoundKey
3540C5F9 E5339290 5DB9DC73 A4A50A87
Round[3] After Mix Columns
05B4679F BBFE7FEE 99538E0F A8E805C9
Round[3] After Inverse Sub Bytes
36C60A6E FE0C6B99 F950E6FB 6FC83612
Round[3] After Inverse Shift Rows
36C8E699 FEC636FB F90C0A12 6F506B6E
Round[2] After Add RoundKey
DADAE017 92444990 F7769FAB 330695AC
Round[2] After Mix Columns
3CB9F381 1354D69E 3F8C2620 9BC9257B
Round[2] After Inverse Sub Bytes
6DDB7E91 82FD4ADF 25F02354 E812C203
Round[2] After Inverse Shift Rows
6D1223DF 82DBC254 25FD7E03 E8F04A91
Round[1] After Add RoundKey
0FEAC90D D0F7A92F DBF1EFF4 CCF2BF34
Round[1] After Mix Columns
D92F5D8A BFD89F59 FD7BAB1C 0D370F80
Round[1] After Inverse Sub Bytes
E54E8DCF F42D6E15 21030EC4 F3B2FB3A
Round[1] After Inverse Shift Rows
E5B20E15 F44EFBC4 212D8D3A F3036ECF
Round[0] After Add Round Key
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[12] Input to Inverse Cipher
97410484 6D0AD3AD 7734ECB3 ECEE4EEF
Round[12] After Add Round Key
7ECAA4EB 2986A491 F9F89EB7 EDEE6CED
Round[12] After Inverse Sub Bytes
8A101D3C 4CDC1DAC 69E1DF20 5399B853
Round[12] After Inverse Shift Rows
8A99DFAC 4C10B820 69DC1D53 53E11D3C
Round[11] After Add RoundKey
40D9DA94 C3DCE826 41F10B39 EFDDFA89
Round[11] After Mix Columns
02C52D3D 5272C031 F7EDA23A A0A73771
Round[11] After Inverse Sub Bytes
6A07FA8B 481E1F2E 26531AA2 4789B22C
Round[11] After Inverse Shift Rows
6A891A2E 4807B2A2 261EFA2C 47531F8B
Round[10] After Add RoundKey
CD685C42 DC16437D A4018F26 EA54C8D8
Round[10] After Mix Columns
FABC06FB 0C1E6086 35F606C9 ACD8C913
Round[10] After Inverse Sub Bytes
1478A563 81E990DC D9D6A512 AA2D1282
Round[10] After Inverse Shift Rows
142DA5DC 81781212 D9E9A582 AAD69063
Round[9] After Add RoundKey
54934EF4 AE60B04B BEAE77E9 EF5AC55D
Round[9] After Mix Columns
110DF190 D7F1A3B0 0592CBD2 683D1860
Round[9] After Inverse Sub Bytes
E3F32B96 0D2B71FC 3674597F F78B3490
Round[9] After Inverse Shift Rows
E38B59FC 0DF3347F 362B2B90 F7747196
Round[8] After Add RoundKey
ABD429CE 2F38B32A D44638C2 C484C625
Round[8] After Mix Columns
5F69F658 D5EF4EFA 73994FCD 807EDF82
Round[8] After Inverse Sub Bytes
84E4D65E B561B614 8FF99280 3A8AEF11
Round[8] After Inverse Shift Rows
848A9214 B5E4EF80 8F61D611 3AF9B65E
Round[7] After Add RoundKey
442C0613 64794B61 637650FA 555FFF2F
Round[7] After Mix Columns
3F3C87F9 76E9379F B50CE3E5 8F8F8A50
Round[7] After Inverse Sub Bytes
256DEA69 0FEBB26E D2814D2A 7373CF6C
Round[7] After Inverse Shift Rows
25734D6E 0F6DCF2A D2EBEA6C 7381B269
Round[6] After Add RoundKey
872D33BB 8CDC00B0 F512D32F 1915450E
Round[6] After Mix Columns
0756F784 8B75DCC2 7BBC6BB7 2390F105
Round[6] After Inverse Sub Bytes
38B9264F CE3F93A8 03780520 32962B36
Round[6] After Inverse Shift Rows
389605A8 CEB92B20 033F2636 3278934F
Round[5] After Add RoundKey
9CDEF371 83D4E504 A90D4556 2343A3A9
Round[5] After Mix Columns
2594D1A0 DFAACE0D 1F9286BC C20A9634
Round[5] After Inverse Sub Bytes
C2E75147 EF62ECF3 CB74DC78 A8A33528
Round[5] After Inverse Shift Rows
C2A3DCF3 EFE73578 CB625128 A874EC47
Round[4] After Add RoundKey
25FC71B7 54EE66FE 8338A17F 899B5D08
Round[4] After Mix Columns
202D4A58 DA8CACD8 0676EEFB 993FC322
Round[4] After Inverse Sub Bytes
54FA5C5E 7AF0AA2D A50F9963 F9253394
Round[4] After Inverse Shift Rows
5425992D 7AFA3363 A5F05C94 F90FAA5E
Round[3] After Add RoundKey
19922D90 134F727B 20571B02 102A92A3
Round[3] After Mix Columns
5962010C FF2E34B0 11B3F63A 09009D9F
Round[3] After Inverse Sub Bytes
15AB0981 7DC328FC E34BD6A2 4052756E
Round[3] After Inverse Shift Rows
1552D6FC 7DAB75A2 E3C3096E 404B2881
Round[2] After Add RoundKey
F940D072 11290AC9 EDB99CD7 1C1DD643
Round[2] After Mix Columns
F770E874 6FA099AD 7DB732E7 43ABBAC6
Round[2] After Inverse Sub Bytes
26D0C8CA 0647F918 1320A1B0 640EC0C7
Round[2] After Inverse Shift Rows
260EA118 06D0C0B0 1347C8C7 6420F9CA
Round[1] After Add RoundKey
44F64BCA 54FCABCB ED4B5930 40220C6F
Round[1] After Mix Columns
B7D7DE8D 1C5C68E0 B175808B A658E817
Round[1] After Inverse Sub Bytes
200D9CB4 C4A7F7A0 563F3ACE C55EC887
Round[1] After Inverse Shift Rows
205E3AA0 C40DC8CE 56A79C87 C53FF7B4
Round[0] After Add Round Key
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[12] Input to Inverse Cipher
EF7AFD22 70E2E60A DCE0BA2F ACE6444E
Round[12] After Add Round Key
06F15D4D 346E9136 522CC82B ADE6664C
Round[12] After Inverse Sub Bytes
A52B8D65 2845AC24 4842B10B 18F5D35D
Round[12] After Inverse Shift Rows
A5F5B124 282BD30B 48458D5D 1842AC65
Round[11] After Add RoundKey
6FB5B41C A7E7830D 60689B37 A47E4BD0
Round[11] After Mix Columns
4EEA71A7 534EF023 4201EA0D E5E588C9
Round[11] After Inverse Sub Bytes
B6BB2C89 50B61732 F609BBF3 2A2A9712
Round[11] After Inverse Shift Rows
B62ABB32 50BB97F3 F6B62C12 2A091789
Round[10] After Add RoundKey
11CBFD5E C4AA662C 74A95918 870EC0DA
Round[10] After Mix Columns
BF59A13E B91853D6 71B07F22 EE93947A
Round[10] After Inverse Sub Bytes
F415F1D1 DB34504A 2CFC6B94 9922E7BD
Round[10] After Inverse Shift Rows
F4226B4A DB15E794 2C34F1BD 99FC50D1
Round[9] After Add RoundKey
B49C8062 F40D45CD 4B7323D6 DC7005EF
Round[9] After Mix Columns
F4B14FC0 3B646846 7F8E96AA 9690C383
Round[9] After Inverse Sub Bytes
BA56921F 498CF798 6BE63562 35963341
Round[9] After Inverse Shift Rows
BA963598 49563362 6B8C9241 35E6F71F
Round[8] After Add RoundKey
F2C945AA 6B9DB437 89E18113 061640AC
Round[8] After Mix Columns
407344A3 3DA108E1 12AFF5B2 7839DD60
Round[8] After Inverse Sub Bytes
728F8671 8BF1BFE0 391B773E C15BC990
Round[8] After Inverse Shift Rows
725B77E0 8B8FC93E 39F18690 C11BBF71
Round[7] After Add RoundKey
B2FDE3E7 5A126DDF D5E6007B AEBDF600
Round[7] After Mix Columns
568C9100 7D9EA5BC F44DB140 7F65F609
Round[7] After Inverse Sub Bytes
B9F0AC52 13DF2978 BA655672 6BBCD640
Round[7] After Inverse Shift Rows
B9BC5678 13F0D672 BADFAC40 6B652952
Round[6] After Add RoundKey
1BE228AD 904119E8 9D269503 01F1DE35
Round[6] After Mix Columns
8FFB444C 0058C9B1 8E91DCEE 685181A3
Round[6] After Inverse Sub Bytes
7363865D 525E1256 E6AC9399 F7709171
Round[6] After Inverse Shift Rows
73709356 52639199 E65E8671 F7AC125D
Round[5] After Add RoundKey
D738658F 1F0E5FBD 4C6CE511 E69722BB
Round[5] After Mix Columns
C14579F8 0C7CB132 B0A4AA6A D0BFDF58
Round[5] After Inverse Sub Bytes
DD68AFE1 810156A1 FC1D6258 60F4EF5E
Round[5] After Inverse Shift Rows
DDF462A1 8168EF58 FC01AF5E 601D56E1
Round[4] After Add RoundKey
3AABCFE5 3A61BCDE B45B5F09 41F2E7AE
Round[4] After Mix Columns
EE547677 48E0BC2D F606743D F9D8B06B
Round[4] After Inverse Sub Bytes
99FD0F02 D4A078FA D6A5CA8B 692DFC05
Round[4] After Inverse Shift Rows
992DCAFA D4FDFC8B D6A00F05 69A57802
Round[3] After Add RoundKey
D49A7E47 BD48BD93 53074893 808040FF
Round[3] After Mix Columns
34F270C1 15A1B8D7 0C6412F5 9DCC38D6
Round[3] After Inverse Sub Bytes
2804D0DD 2FF19A0D 818C3977 7527764A
Round[3] After Inverse Shift Rows
2827390D 2F047677 81F1D04A 758C9ADD
Round[2] After Add RoundKey
C4353F83 4386091C 8F8B45F3 29DA641F
Round[2] After Mix Columns
EFDC8EF0 EBD71AF6 D7A262A5 5F2019EE
Round[2] After Inverse Sub Bytes
6193E617 3C0D43D6 0D1AAB29 84548E99
Round[2] After Inverse Shift Rows
6154ABD6 3C938E29 0D0DE699 841A4317
Round[1] After Add RoundKey
03AC4104 6EBFE552 F301776E A018B6B2
Round[1] After Mix Columns
AE002367 B6E9F1C8 D8B8911A B8EACD23
Round[1] After Inverse Sub Bytes
BE52320A 79EB2BB1 2D9AAC43 9ABB8032
Round[1] After Inverse Shift Rows
BEBBACB1 79528043 2DEB3232 9A9A2B0A
Round[0] After Add Round Key
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[12] Input to Inverse Cipher
9A4B41BA 738D6C72 FB166916 03C18E0E
Round[12] After Add Round Key
73C0E1D5 37011B4E 75DA1B12 02C1AC0C
Round[12] After Inverse Sub Bytes
8F1FE0B5 B20944B6 3F7A4439 6ADDAA81
Round[12] After Inverse Shift Rows
8FDD44B6 B21FAA39 3F09E081 6A7A44B5
Round[11] After Add RoundKey
459D418E 3DD3FA3F 1724F6EB D646A300
Round[11] After Mix Columns
51DD7BE0 A37432CE 9DCF205C 92248104
Round[11] After Inverse Sub Bytes
70C903A0 71CAA1EC 755F54A7 74A69130
Round[11] After Inverse Shift Rows
70A654EC 71C991A7 75CA0330 745FA1A0
Round[10] After Add RoundKey
D7471280 E5D86078 F7D5763A D95876F3
Round[10] After Mix Columns
C7CE060D AB1364F9 B22AEF19 6EBAC919
Round[10] After Inverse Sub Bytes
31ECA5F3 0E828C69 3E95618E 45C0128E
Round[10] After Inverse Shift Rows
31C06169 0EEC128E 3E82A58E 45958CF3
Round[9] After Add RoundKey
717E8A41 21F4B0D7 59C577E5 0019D9CD
Round[9] After Mix Columns
10CF7863 B7A559F9 BC448E78 1E9ADD54
Round[9] After Inverse Sub Bytes
7C5FC100 20291569 7886E6C1 E937C9FD
Round[9] After Inverse Shift Rows
7C37E669 205FC9C1 7829C1FD E9861500
Round[8] After Add RoundKey
3468965B 02944E94 9A44D2AF DA76A2B3
Round[8] After Mix Columns
4736DC3C 0421D0B9 CA3EDF88 40DE597A
Round[8] After Inverse Sub Bytes
1624936D 307B60DB 10D1EF97 729C15BD
Round[8] After Inverse Shift Rows
169CEFDB 30241597 107B93BD 72D1606D
Round[7] After Add RoundKey
D63A7BDC E1B9B176 FC6C1556 1D77291C
Round[7] After Mix Columns
B2288958 01B37459 5F670BE0 88ED0238
Round[7] After Inverse Sub Bytes
3EEEF25E 094BCA15 840A9EA0 97536A76
Round[7] After Inverse Shift Rows
3E539E15 09EE6AA0 844BF276 970ACA5E
Round[6] After Add RoundKey
9C0DE0C0 8A5FA53A A3B2CB35 FD9E3D39
Round[6] After Mix Columns
009B052F AB1310E2 ECBC41FE 641B6A72
Round[6] After Inverse Sub Bytes
52E8364E 0E827C3B 8378F80C 8C44581E
Round[6] After Inverse Shift Rows
5244F83B 0EE8580C 8382361E 8C787C4E
Round[5] After Add RoundKey
F60C0EE2 43859628 29B0557E 9D434CA8
Round[5] After Mix Columns
723BA6F9 38B41DE9 BE21BD90 A22D07B2
Round[5] After Inverse Sub Bytes
1E49C569 76C6DEEB 5A7BCD96 1AFA383E
Round[5] After Inverse Shift Rows
1EFACDEB 76493896 5AC6C53E 1A7BDE69
Round[4] After Add RoundKey
F9A560AF CD406B10 129C3569 3B946F26
Round[4] After Mix Columns
747BD04C 654A34ED 9134097E A2102175
Round[4] After Inverse Sub Bytes
CA03605D BC5C2853 AC28408A 1A7C7B3F
Round[4] After Inverse Shift Rows
CA7C4053 BC037B8A AC5C603F 1A28285D
Round[3] After Add RoundKey
87CBF4EE D5B63A92 29FB27A9 F30D10A0
Round[3] After Mix Columns
18F1C778 4BEC2945 2481926B BDBDC28C
Round[3] After Inverse Sub Bytes
342B31C1 CC834C68 A6917405 CDCDA8F0
Round[3] After Inverse Shift Rows
34CD7468 CC2BA805 A68331F0 CD914CC1
Round[2] After Add RoundKey
D8DF72E6 A0A9D76E A8F9A449 91C7B203
Round[2] After Mix Columns
2F1DB819 32233E9F 119E7E4D 2F8ED99F
Round[2] After Inverse Sub Bytes
4EDE9A8E A132D16E E3DF8A65 4EE6E56E
Round[2] After Inverse Shift Rows
4EE68A6E A1DEE565 E3329A6E 4EDFD18E
Round[1] After Add RoundKey
2C1E60BC F3F28E1E 1D3E0B99 6ADD242B
Round[1] After Mix Columns
BC8337E6 6BE22F37 4DB0226E 33CE1653
Round[1] After Inverse Sub Bytes
7841B2F5 053B4EB2 65FC9445 66ECFF50
Round[1] After Inverse Shift Rows
78EC94B2 0541FF45 653BB250 66FC4EF5
Round[0] After Add Round Key
F69F2445 DF4F9B17 AD2B417B E66C3710
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
Enter option = 7
NIST Standard Test Data
256-Bit Cipher Key
603DEB10 15CA71BE 2B73AEF0 857D7781 1F352C07 3B6108D7 2D9810A3 0914DFF4
Electronic Codebook (ECB) Mode
ECB-AES256 (Encryption)
NIST Standard Test Data
AES-256 (Nk = 8, Nr = 14)
Test Vectors
Round[0] Input to Cipher
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[0] After Add Round Key
0BFC55F2 3B8AEE28 C24ED0E1 F6EE60AB
Round[1] After Sub Bytes
2BB0FC89 E27E2834 252F70F8 4228D062
Round[1] After Shift Rows
2B7E7062 E22FD089 2528FC34 42B028F8
Round[1] After Mix Columns
C62513B7 F75EF6CB FA5EB2D3 9FB9B1B5
Round[1] After Add Round Key
D9103FB0 CC3FFE1C D7C6A270 96AD6E41
Round[2] After Sub Bytes
35CA75E7 4B75BB9C 0EB43A51 90959F83
Round[2] After Shift Rows
35753A83 4BB49FE7 0E95759C 90CABB51
Round[2] After Mix Columns
4C12AA0D 2965E823 513CCED1 9498C478
Round[2] After Add Round Key
D7B1FE1C A70CCD8C F426458E B4FF38A6
Round[3] After Sub Bytes
0EC8BB9C 5CFEBD64 BFF76E19 8D160724
Round[3] After Shift Rows
0EFE6E24 5CF7079C BF16BB64 8DC8BD19
Round[3] After Mix Columns
4F7F40CA 213C1A37 802168BF E6C30FCB
Round[3] After Add Round Key
E7CFDCD0 B2ED8EFA 3E68ECD1 519E5451
Round[4] After Sub Bytes
948A8670 3755192D B245CE3E D10B20D1
Round[4] After Shift Rows
9455CED1 37452070 B20B862D D18A193E
Round[4] After Mix Columns
D3A62E85 F1ADA2DC C918D91A 1BCB2B87
Round[4] After Add Round Key
063CC23D AA5E6BCB 37F19B52 C5459511
Round[5] After Sub Bytes
6FEB2527 AC587F1F 9AA11400 A66E2A82
Round[5] After Shift Rows
6F581482 ACA12A27 9A6E251F A6EB7F00
Round[5] After Mix Columns
A06182E2 B6AC302A A7369FC0 0EEAB365
Round[5] After Add Round Key
15C8B068 90D4966D 3F07BDE9 2186CAD6
Round[6] After Sub Bytes
59E8E745 6048903C 75C57A1E FD4474F6
Round[6] After Shift Rows
59487AF6 60C57445 7544E73C FDE8901E
Round[6] After Mix Columns
E6B1E42E A528829B FDF3A044 4C830C58
Round[6] After Add Round Key
679D6583 7FF7CA21 D9C5AAB6 B63BB83C
Round[7] After Sub Bytes
855E4DEC D26874FD 35A6AC4E 4EE26CEB
Round[7] After Shift Rows
8568ACEB D2A66CEC 35E24DFD 4E5E744E
Round[7] After Mix Columns
EE51889D CEDD8364 E7C05111 44202A64
Round[7] After Add Round Key
76943754 70609AEA C14C6AB6 4DC06870
Round[8] After Sub Bytes
38229A20 51D0B887 7829024E E3BA4551
Round[8] After Shift Rows
38D00251 51294520 78BA9A87 E322B84E
Round[8] After Mix Columns
48D41F38 BCEC92DF 38257FBD 4D3A7838
Round[8] After Add Round Key
20D46494 0E33A1C9 AECC4659 216BF5B8
Round[9] After Sub Bytes
B7484322 ABC332DD E44B5ACB FD7FE66C
Round[9] After Shift Rows
B7C35A6C AB4BE622 E47F43DD FD4832CB
Round[9] After Mix Columns
1DA87483 542E510F CC0261AA C0F097EB
Round[9] After Add Round Key
D5BC9687 2287AA85 9C27A187 993515D2
Round[10] After Sub Bytes
03659017 9317AC97 DECC3217 EE9659B5
Round[10] After Shift Rows
031732B5 93CC5917 DE969097 EE65AC17
Round[10] After Mix Columns
B8CEB451 3CECD415 01D5D14A D3DCF1CE
Round[10] After Add Round Key
66DDDD36 50208E64 FBF0B2DF 45A81FDB
Round[11] After Sub Bytes
33C1C105 53B71943 0F8C379E 6EC2C0B9
Round[11] After Shift Rows
33B737B9 538CC005 0FC2C143 6EC1199E
Round[11] After Mix Columns
2AA63ABC EC0E4BB3 C18B9194 0342244D
Round[11] After Add Round Key
7220F0E1 C2217A64 BF81606E 248D578E
Round[12] After Sub Bytes
40B78CF8 25FDDA43 080CD09F 365D5B19
Round[12] After Shift Rows
40FDD019 250C5BF8 085D8C43 36B7DA9F
Round[12] After Mix Columns
55D32DDF FD288CD3 387E934F EBA99412
Round[12] After Add Round Key
214F6A74 E5789109 DA0BED00 9FA80448
Round[13] After Sub Bytes
FD840292 D9BC8101 572B5563 DBC2F252
Round[13] After Shift Rows
FDBC5552 D92BF292 57C20201 DB848163
Round[13] After Mix Columns
39331D51 B410A096 F0CF923B D833E3B5
Round[13] After Add Round Key
F3C9B7B2 50C53BA2 6A10F8F5 6523FAB8
Round[14] After Sub Bytes
0DDDA937 53A6E23A 02CA41E6 4D262D6C
Round[14] After Shift Rows
0DA6416C 53CA2D37 0226A93A 4DDDE2E6
Round[14] After Add Round Key
F3EED1BD B5D2A03C 064B5A7E 3DB181F8
Round[0] Input to Cipher
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[0] After Add Round Key
CE106147 0BC9DD22 B5C4C15C C0D2F9D0
Round[1] After Sub Bytes
8BCAEFA0 2BDDC193 D51C784A BAB59970
Round[1] After Shift Rows
8BDD7870 2B1C99A0 D5B5EF93 BACAC14A
Round[1] After Mix Columns
79D236C3 4B03E5A3 091D0B03 A127374A
Round[1] After Add Round Key
66E71AC4 7062ED74 24851BA0 A833E8BE
Round[2] After Sub Bytes
3394A21C 51AA5592 3697AFE0 C2C39BAE
Round[2] After Shift Rows
33AAAFAE 51979B1C 36C3A292 C29455E0
Round[2] After Mix Columns
82383517 87CECFC7 02C40704 8DEEC747
Round[2] After Add Round Key
199B6106 09A7EA68 A7DE8C5B AD893B99
Round[3] After Sub Bytes
D414EF6F 015C8745 5C1D6439 95A7E2EE
Round[3] After Shift Rows
D45C64EE 011DE26F 5CA7EF45 95148739
Round[3] After Mix Columns
DD2E6998 A8697222 E066F126 B316DF45
Round[3] After Add Round Key
759EF582 3BB8E6EF 5E2F7548 044B84DF
Round[4] After Sub Bytes
9D0BE613 E26C8EDF 58159D52 F2B35F9E
Round[4] After Shift Rows
9D6C9D9E E2155F13 58B3E6DF F20B8E52
Round[4] After Mix Columns
9667696A AC3A7C51 47CB4618 3E3F082C
Round[4] After Add Round Key
43FD85D2 F7C9B546 B9220450 E0B1B6BA
Round[5] After Sub Bytes
1A5497B5 68DDD55A 5693F253 E1C84EF4
Round[5] After Shift Rows
1ADDF2F4 68934EB5 56C8975A E154D553
Round[5] After Mix Columns
4E423FF2 8532A314 22254511 A37EF11F
Round[5] After Add Round Key
FBEB0D78 A34A0553 BA146738 8C1288AC
Round[6] After Sub Bytes
0FE9D7BC 0AD66BED F4FA8507 64C9C491
Round[6] After Shift Rows
0FD68591 0AFAC4BC F4C9D7ED 64E96B07
Round[6] After Mix Columns
6BBD607B 790EBC43 89F2A4D8 84175220
Round[6] After Add Round Key
EA91E1D6 A3D1F4F9 ADC4AE2A 7EAFE644
Round[7] After Sub Bytes
8781F8F6 0A3EBF99 951CE4E5 F3798E1B
Round[7] After Shift Rows
873EE41B 0A1C8EF6 9579F899 F381BFE5
Round[7] After Mix Columns
A8D7477E 484D107B DBEDB70C 3FD523E1
Round[7] After Add Round Key
3012F8B7 F6F009F5 FD618CAB 363561F5
Round[8] After Sub Bytes
04C941A9 428C01E6 54EF6462 0596EFE6
Round[8] After Shift Rows
048C64E6 42EFEFA9 549641E6 05C90162
Round[8] After Mix Columns
054D7133 E804888F AE4671FC 29ED6803
Round[8] After Add Round Key
6D4D0A9F 5ADBBB99 38AF4818 45BCE583
Round[9] After Sub Bytes
3CE367DB BEB9EAEE 077952AD 6E65D9EC
Round[9] After Shift Rows
3CB952EC BE79D9DB 076567EE 6EE3EAAD
Round[9] After Mix Columns
164F0E6C EEE718D4 288A85CC A53BAEFA
Round[9] After Add Round Key
DE5BEC68 984EE35E 78AF45E1 FCFE2CC3
Round[10] After Sub Bytes
1D39CE45 462F1158 BC796EF8 B0BB712E
Round[10] After Shift Rows
1D2F6E2E 46797145 BCBBCE58 B03911F8
Round[10] After Mix Columns
0BDF9C3A 33621248 23C0681A D909B808
Round[10] After Add Round Key
D5CCF55D 5FAE4839 D9E50B8F 4F7D561D
Round[11] After Sub Bytes
034BE64C CFE45212 35D92B73 84FFB1A4
Round[11] After Shift Rows
03E42BA4 CFD9B14C 35FFE612 844B5273
Round[11] After Mix Columns
BE094699 08E2BBBA 84F32B62 EF97FE68
Round[11] After Add Round Key
E68F8CC4 26CD8A6D FAF9DA98 C8588DAB
Round[12] After Sub Bytes
8E73641C F7BD7E3C 2D995746 E86A5D62
Round[12] After Shift Rows
8EBD5762 F7995D1C 2D6A643C E8737E46
Round[12] After Mix Columns
EE743BA7 0425F0FE BC69CB01 66CAADA2
Round[12] After Add Round Key
9AE87C0C 1C75ED24 5E1CB54E 12CB3DF8
Round[13] After Sub Bytes
B89B10FE 9C9D5536 589CD52F C91F2741
Round[13] After Shift Rows
B89DD541 9C9C27FE 581F1036 C99B552F
Round[13] After Mix Columns
43BC5719 452857E3 B7603D8B 453489D0
Round[13] After Add Round Key
8946FDFA A1FDCCD7 2DBF5745 F82490DD
Round[14] After Sub Bytes
A75A542D 32544B0E D8085B6E 413660C1
Round[14] After Shift Rows
A7545BC1 3208602D D836540E 415A4B6E
Round[14] After Add Round Key
591CCB10 D410ED26 DC5BA74A 31362870
Round[0] Input to Cipher
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[0] After Add Round Key
50F5F756 B69695AF CE886FE9 9F77256E
Round[1] After Sub Bytes
53E668B1 4E902A79 8BC4A81E DBF53F9F
Round[1] After Shift Rows
5390A89F 4EC43FB1 8BF56879 DBE62A1E
Round[1] After Mix Columns
3A1432E8 452D3C50 18BB25E9 A86C4B86
Round[1] After Add Round Key
25211EEF 7E4C3487 3523354A A1789472
Round[2] After Sub Bytes
3FFD72DF F3291817 962696D6 32BC2240
Round[2] After Shift Rows
3F299640 F32622DF 96BC7217 32FD18D6
Round[2] After Mix Columns
D38CE17E 6A06EBAF 8D74F741 B62D9E04
Round[2] After Add Round Key
482FB56F E46FCE00 286E7C1E 964A62DA
Round[3] After Sub Bytes
5215D5A8 69A88B63 349F1072 90D6AA57
Round[3] After Shift Rows
52A81057 699FAAA8 34D6D563 90158B72
Round[3] After Mix Columns
007E23E0 6A015AC5 BF84F699 FD4E1ED1
Round[3] After Add Round Key
A8CEBFFA F9D0CE08 01CD72F7 4A13454B
Round[4] After Sub Bytes
C28B082D 99708B30 7CBD4068 D67D6EB3
Round[4] After Shift Rows
C27040B3 99BD6E2D 7C7D0830 D68B8B68
Round[4] After Mix Columns
FC51FC10 B6678F39 47AE4191 D235E8B1
Round[4] After Add Round Key
29CB10A8 ED94462E B94703D9 0CBB5627
Round[5] After Sub Bytes
A51FCAC2 55225A31 56A07B35 FEEAB1CC
Round[5] After Shift Rows
A5227BCC 55A0B1C2 56EACA31 FE1F5A35
Round[5] After Mix Columns
80A03E2E 2204D171 72ED60B8 A91B0A36
Round[5] After Add Round Key
35090CA4 047C7736 EADC4291 86777385
Round[6] After Sub Bytes
9601FE49 F210F505 87862C81 44F58F97
Round[6] After Shift Rows
96102C97 F2868F49 87F5FE05 4401F581
Round[6] After Mix Columns
BC557CA8 A826AA96 EA6A9A93 FFC32C21
Round[6] After Add Round Key
3D79FD05 72F9E22C CE5C9061 057B9845
Round[7] After Sub Bytes
27B6546B 40999871 8B4A60EF 6B21466E
Round[7] After Shift Rows
2799606E 404A466B 8B215471 6BB698EF
Round[7] After Mix Columns
F0C0CC4C 73753B1A 4B449111 6040DC56
Round[7] After Add Round Key
68057385 CDC82294 6DC8AAB6 69A09E42
Round[8] After Sub Bytes
456B8F97 BDE89322 3CE8AC4E F9E00B2C
Round[8] After Shift Rows
45E8AC2C BDE80B97 3CE08F22 F96B934E
Round[8] After Mix Columns
294D9AD3 DEFCE10A EE4FBF6F 89CF7D74
Round[8] After Add Round Key
414DE17F 6C23D21C 78A6868B E59EF0F4
Round[9] After Sub Bytes
83E3F8D2 5026B59C BC24443D D90B8CBF
Round[9] After Shift Rows
832644BF 50248CD2 BC0BF89C D9E3B53D
Round[9] After Mix Columns
8CBCF799 92451AE7 1A25E30F 1FFD0C5C
Round[9] After Add Round Key
44A8159D E4ECE16D 4A002322 46388E65
Round[10] After Sub Bytes
1BC2595E 69CEF83C D6632693 5A07194D
Round[10] After Shift Rows
1BCE264D 6963195E D607593C 5AC2F893
Round[10] After Mix Columns
14BB4E5F 30DADA7D DB0F2747 8245DDE9
Round[10] After Add Round Key
CAA82738 5C16800C 212A44D2 143133FC
Round[11] After Sub Bytes
74C2CC07 4A47CDFE FDE51BB5 FAC7C3B0
Round[11] After Shift Rows
74471BB0 4AE5C307 FDC7CCFE FAC2CDB5
Round[11] After Mix Columns
8A67CEBB 64C23BF6 81D9A0F0 CA9C7D6B
Round[11] After Add Round Key
D2E104E6 4AED0A21 FFD3510A ED530EA8
Round[12] After Sub Bytes
B5F8F28E D65567FD 1666D167 55EDABC2
Round[12] After Shift Rows
B555D1C2 D666AB8E 16EDF2FD 55F86767
Round[12] After Mix Columns
9DB504DF 387274AB 0F2718C4 B970CAAE
Round[12] After Add Round Key
E9294374 20226971 ED52668B CD715AF4
Round[13] After Sub Bytes
1EA51A92 B793F9A3 5500333D BDA3BEBF
Round[13] After Shift Rows
1E9333BF B700BE92 55A31AA3 BDA5F93D
Round[13] After Mix Columns
1EC931E7 59FC7D43 ED853C1B 51C1B6FA
Round[13] After Add Round Key
D4339B04 BD29E677 775A56D5 ECD1AFF7
Round[14] After Sub Bytes
48C314F2 7AA58EF5 F5BEB103 CE3E7968
Round[14] After Shift Rows
48A5B168 7ABE79F2 F53E14F5 CEC38E03
Round[14] After Add Round Key
B6ED21B9 9CA6F4F9 F153E7B1 BEAFED1D
Round[0] Input to Cipher
F69F2445 DF4F9B17 AD2B417B E66C3710
Round[0] After Add Round Key
96A2CF55 CA85EAA9 8658EF8B 63114091
Round[1] After Sub Bytes
903A8AFC 749787D3 446ADF3D FB820981
Round[1] After Shift Rows
9097DF81 746A09FC 44828AD3 FB3A873D
Round[1] After Mix Columns
C75E3AFA A347131C 4C0DA779 192093D1
Round[1] After Add Round Key
D86B16FD 98261BCB 6195B7DA 10344C25
Round[2] After Sub Bytes
617F4754 46F7AF1F EF2AA957 CA18293F
Round[2] After Shift Rows
61F7A93F 462A2954 EF18471F CA7FAF57
Round[2] After Mix Columns
564B9E83 8F3DC261 B509584B F689093B
Round[2] After Add Round Key
CDE8CA92 0154E7CE 1013D314 D6EEF5E5
Round[3] After Sub Bytes
BD9B744F 7C20948B CA7D66FA F628E6D9
Round[3] After Shift Rows
BD2066D9 7C7DE64F CA28748B F69B94FA
Round[3] After Mix Columns
BE8E2133 D6F80781 088D8C14 2F864BE1
Round[3] After Add Round Key
163EBD29 4529934C B6C4087A 98DB107B
Round[4] After Sub Bytes
47B27AA5 6EA5DC29 4E1C30DA 46B9CA21
Round[4] After Shift Rows
47A53021 6E1CCAA5 4EB97A29 46B2DCDA
Round[4] After Mix Columns
6B67E11E 97B60935 1F807843 479C220B
Round[4] After Add Round Key
BEFD0DA6 CC45C022 E1693A0B 99129C9D
Round[5] After Sub Bytes
AE54D724 4B6EBA93 F8F9802B EEC9DE5E
Round[5] After Shift Rows
AE6E805E 4BF9DE24 F8C9D793 EE54BA2B
Round[5] After Mix Columns
2BB739BB 7CFF79B2 EF802A30 AAB8A891
Round[5] After Add Round Key
9E1E0B31 5A87DFF5 77B10819 85D4D122
Round[6] After Sub Bytes
0B722BC7 BE179EE6 F5C830D4 97483E93
Round[6] After Shift Rows
0B173093 BEC83EC7 F5482BE6 97729ED4
Round[6] After Mix Columns
8CE6D207 DDB058BA E4FEDAB0 E91EA5FD
Round[6] After Add Round Key
0DCA53AA 076F1000 C0C8D042 13A61199
Round[7] After Sub Bytes
D774EDAC C5A8CA63 BAE8702C 7D2482EE
Round[7] After Shift Rows
D7A870EE C5E882AC BA24ED63 7D74CA2C
Round[7] After Mix Columns
C8E2B67D 9C3FDD7D 8DBDFADA 80FCF261
Round[7] After Add Round Key
502709B4 2282C4F3 AB31C17D 891CB075
Round[8] After Sub Bytes
53CC018D 93131C0D 62C778FF A79CE79D
Round[8] After Shift Rows
5313789D 93C7E78D 629C010D A7CC1CFF
Round[8] After Mix Columns
76600CBF 05B90D8F 774FEB21 F9FF49C7
Round[8] After Add Round Key
1E607713 B7663E99 E1A6D2C5 95AEC447
Round[9] After Sub Bytes
72D0F57D A933B2EE F824B5A6 2AE41CA0
Round[9] After Shift Rows
7233B5A0 A9241C7D F8E4F5EE 2AD0B2A6
Round[9] After Mix Columns
A470CB4B 44B83222 C7C1C4C5 2BFA744B
Round[9] After Add Round Key
6C64294F 3211C9A8 97E404E8 723FF672
Round[10] After Sub Bytes
5043A584 2382DDC2 8869F29B 40754240
Round[10] After Shift Rows
5082F240 23694284 8875A5C2 4043DD9B
Round[10] After Mix Columns
8F02ED00 3BB3595D F354F1CC 03211473
Round[10] After Add Round Key
51118467 577F032C 09719259 9555FA66
Round[11] After Sub Bytes
D1825F85 5BD27B71 01A34FCB 2AFC2D33
Round[11] After Shift Rows
D1D24F33 5BA32D85 01FC5F71 2A827BCB
Round[11] After Mix Columns
A88CC893 E0F43672 3372D042 7973180A
Round[11] After Add Round Key
F00A02CE CEDB07A5 4D7821B8 5EBC6BC9
Round[12] After Sub Bytes
8C67778B 8BB9C506 E3BCFD6C 58657FDD
Round[12] After Shift Rows
8CB9FDDD 8BBC7F8B E3657706 5867C56C
Round[12] After Mix Columns
F324A86A 26E24F48 03B66220 B0AE1A92
Round[12] After Add Round Key
87B8EFC1 3EB25292 E1C31C6F C4AF8AC8
Round[13] After Sub Bytes
176CDF78 B237004F F82E9CA8 1C797EE8
Round[13] After Shift Rows
17379CE8 B22E7E78 F879DF4F 1C6C00A8
Round[13] After Mix Columns
032E2059 0B14E86D F03FF52B 246C9303
Round[13] After Add Round Key
C9D48ABA EFC17359 6AE09FE5 997C8A0E
Round[14] After Sub Bytes
DD487EF4 DF788FCB 02E1DBD9 EE107EAB
Round[14] After Shift Rows
DD78DBAB DFE17EF4 02107ECB EE488FD9
Round[14] After Add Round Key
23304B7A 39F9F3FF 067D8D8F 9E24ECC7
== Menu ==
1 Detailed NIST FIPS 197 128-Bit Encryption
2 Detailed NIST FIPS 197 128-Bit Decryption
3 ECB Encryption 128-Bit Test Vectors
4 ECB Decryption 128-Bit Test Vectors
5 ECB Encryption 192-Bit Test Vectors
6 ECB Decryption 192-Bit Test Vectors
7 ECB Encryption 256-Bit Test Vectors
8 ECB Decryption 256-Bit Test Vectors
9 Exit
Enter option = 8
NIST Standard Test Data
256-Bit Cipher Key
603DEB10 15CA71BE 2B73AEF0 857D7781 1F352C07 3B6108D7 2D9810A3 0914DFF4
Electronic Codebook (ECB) Mode
ECB-AES256 (Decryption)
NIST Standard Test Data
AES-256 (Nk = 8, Nr = 14)
Test Vectors
Round[14] Input to Inverse Cipher
F3EED1BD B5D2A03C 064B5A7E 3DB181F8
Round[14] After Add Round Key
0DA6416C 53CA2D37 0226A93A 4DDDE2E6
Round[14] After Inverse Sub Bytes
F3C5F8B8 5010FAB2 6A23B7A2 65C93BF5
Round[14] After Inverse Shift Rows
F3C9B7B2 50C53BA2 6A10F8F5 6523FAB8
Round[13] After Add RoundKey
39331D51 B410A096 F0CF923B D833E3B5
Round[13] After Mix Columns
FDBC5552 D92BF292 57C20201 DB848163
Round[13] After Inverse Sub Bytes
2178ED48 E50B0474 DAA86A09 9F4F9100
Round[13] After Inverse Shift Rows
214F6A74 E5789109 DA0BED00 9FA80448
Round[12] After Add RoundKey
55D32DDF FD288CD3 387E934F EBA99412
Round[12] After Mix Columns
40FDD019 250C5BF8 085D8C43 36B7DA9F
Round[12] After Inverse Sub Bytes
7221608E C28157E1 BF8DF064 24207A6E
Round[12] After Inverse Shift Rows
7220F0E1 C2217A64 BF81606E 248D578E
Round[11] After Add RoundKey
2AA63ABC EC0E4BB3 C18B9194 0342244D
Round[11] After Mix Columns
33B737B9 538CC005 0FC2C143 6EC1199E
Round[11] After Inverse Sub Bytes
6620B2DB 50F01F36 FBA8DD64 45DD8EDF
Round[11] After Inverse Shift Rows
66DDDD36 50208E64 FBF0B2DF 45A81FDB
Round[10] After Add RoundKey
B8CEB451 3CECD415 01D5D14A D3DCF1CE
Round[10] After Mix Columns
031732B5 93CC5917 DE969097 EE65AC17
Round[10] After Inverse Sub Bytes
D587A1D2 22271587 9C359685 99BCAA87
Round[10] After Inverse Shift Rows
D5BC9687 2287AA85 9C27A187 993515D2
Round[9] After Add RoundKey
1DA87483 542E510F CC0261AA C0F097EB
Round[9] After Mix Columns
B7C35A6C AB4BE622 E47F43DD FD4832CB
Round[9] After Inverse Sub Bytes
203346B8 0ECCF594 AE6B64C9 21D4A159
Round[9] After Inverse Shift Rows
20D46494 0E33A1C9 AECC4659 216BF5B8
Round[8] After Add RoundKey
48D41F38 BCEC92DF 38257FBD 4D3A7838
Round[8] After Mix Columns
38D00251 51294520 78BA9A87 E322B84E
Round[8] After Inverse Sub Bytes
76606A70 704C6854 C1C037EA 4D949AB6
Round[8] After Inverse Shift Rows
76943754 70609AEA C14C6AB6 4DC06870
Round[7] After Add RoundKey
EE51889D CEDD8364 E7C05111 44202A64
Round[7] After Mix Columns
8568ACEB D2A66CEC 35E24DFD 4E5E744E
Round[7] After Inverse Sub Bytes
67F7AA3C 7FC5B883 D93B6521 B69DCAB6
Round[7] After Inverse Shift Rows
679D6583 7FF7CA21 D9C5AAB6 B63BB83C
Round[6] After Add RoundKey
E6B1E42E A528829B FDF3A044 4C830C58
Round[6] After Mix Columns
59487AF6 60C57445 7544E73C FDE8901E
Round[6] After Inverse Sub Bytes
15D4BDD6 9007CA68 3F86B06D 21C896E9
Round[6] After Inverse Shift Rows
15C8B068 90D4966D 3F07BDE9 2186CAD6
Round[5] After Add RoundKey
A06182E2 B6AC302A A7369FC0 0EEAB365
Round[5] After Mix Columns
6F581482 ACA12A27 9A6E251F A6EB7F00
Round[5] After Inverse Sub Bytes
065E9B11 AAF1953D 3745C2CB C53C6B52
Round[5] After Inverse Shift Rows
063CC23D AA5E6BCB 37F19B52 C5459511
Round[4] After Add RoundKey
D3A62E85 F1ADA2DC C918D91A 1BCB2B87
Round[4] After Mix Columns
9455CED1 37452070 B20B862D D18A193E
Round[4] After Inverse Sub Bytes
E7EDEC51 B26854D0 3E9EDCFA 51CF8ED1
Round[4] After Inverse Shift Rows
E7CFDCD0 B2ED8EFA 3E68ECD1 519E5451
Round[3] After Add RoundKey
4F7F40CA 213C1A37 802168BF E6C30FCB
Round[3] After Mix Columns
0EFE6E24 5CF7079C BF16BB64 8DC8BD19
Round[3] After Inverse Sub Bytes
D70C45A6 A726381C F4FFFE8C B4B1CD8E
Round[3] After Inverse Shift Rows
D7B1FE1C A70CCD8C F426458E B4FF38A6
Round[2] After Add RoundKey
4C12AA0D 2965E823 513CCED1 9498C478
Round[2] After Mix Columns
35753A83 4BB49FE7 0E95759C 90CABB51
Round[2] After Inverse Sub Bytes
D93FA241 CCC66EB0 D7AD3F1C 9610FE70
Round[2] After Inverse Shift Rows
D9103FB0 CC3FFE1C D7C6A270 96AD6E41
Round[1] After Add RoundKey
C62513B7 F75EF6CB FA5EB2D3 9FB9B1B5
Round[1] After Mix Columns
2B7E7062 E22FD089 2528FC34 42B028F8
Round[1] After Inverse Sub Bytes
0B8AD0AB 3B4E60F2 C2EE5528 F6FCEEE1
Round[1] After Inverse Shift Rows
0BFC55F2 3B8AEE28 C24ED0E1 F6EE60AB
Round[0] After Add Round Key
6BC1BEE2 2E409F96 E93D7E11 7393172A
Round[14] Input to Inverse Cipher
591CCB10 D410ED26 DC5BA74A 31362870
Round[14] After Add Round Key
A7545BC1 3208602D D836540E 415A4B6E
Round[14] After Inverse Sub Bytes
89FD57DD A1BF90FA 2D24FDD7 F846CC45
Round[14] After Inverse Shift Rows
8946FDFA A1FDCCD7 2DBF5745 F82490DD
Round[13] After Add RoundKey
43BC5719 452857E3 B7603D8B 453489D0
Round[13] After Mix Columns
B89DD541 9C9C27FE 581F1036 C99B552F
Round[13] After Inverse Sub Bytes
9A75B5F8 1C1C3D0C 5ECB7C24 12E8ED4E
Round[13] After Inverse Shift Rows
9AE87C0C 1C75ED24 5E1CB54E 12CB3DF8
Round[12] After Add RoundKey
EE743BA7 0425F0FE BC69CB01 66CAADA2
Round[12] After Mix Columns
8EBD5762 F7995D1C 2D6A643C E8737E46
Round[12] After Inverse Sub Bytes
E6CDDAAB 26F98DC4 FA588C6D C88F8A98
Round[12] After Inverse Shift Rows
E68F8CC4 26CD8A6D FAF9DA98 C8588DAB
Round[11] After Add RoundKey
BE094699 08E2BBBA 84F32B62 EF97FE68
Round[11] After Mix Columns
03E42BA4 CFD9B14C 35FFE612 844B5273
Round[11] After Inverse Sub Bytes
D5AE0B1D 5FE5565D D97DF539 4FCC488F
Round[11] After Inverse Shift Rows
D5CCF55D 5FAE4839 D9E50B8F 4F7D561D
Round[10] After Add RoundKey
0BDF9C3A 33621248 23C0681A D909B808
Round[10] After Mix Columns
1D2F6E2E 46797145 BCBBCE58 B03911F8
Round[10] After Inverse Sub Bytes
DE4E45C3 98AF2C68 78FEEC5E FC5BE3E1
Round[10] After Inverse Shift Rows
DE5BEC68 984EE35E 78AF45E1 FCFE2CC3
Round[9] After Add RoundKey
164F0E6C EEE718D4 288A85CC A53BAEFA
Round[9] After Mix Columns
3CB952EC BE79D9DB 076567EE 6EE3EAAD
Round[9] After Inverse Sub Bytes
6DDB4883 5AAFE59F 38BC0A99 454DBB18
Round[9] After Inverse Shift Rows
6D4D0A9F 5ADBBB99 38AF4818 45BCE583
Round[8] After Add RoundKey
054D7133 E804888F AE4671FC 29ED6803
Round[8] After Mix Columns
048C64E6 42EFEFA9 549641E6 05C90162
Round[8] After Inverse Sub Bytes
30F08CF5 F66161B7 FD35F8F5 361209AB
Round[8] After Inverse Shift Rows
3012F8B7 F6F009F5 FD618CAB 363561F5
Round[7] After Add RoundKey
A8D7477E 484D107B DBEDB70C 3FD523E1
Round[7] After Mix Columns
873EE41B 0A1C8EF6 9579F899 F381BFE5
Round[7] After Inverse Sub Bytes
EAD1AE44 A3C4E6D6 ADAFE1F9 7E91F42A
Round[7] After Inverse Shift Rows
EA91E1D6 A3D1F4F9 ADC4AE2A 7EAFE644
Round[6] After Add RoundKey
6BBD607B 790EBC43 89F2A4D8 84175220
Round[6] After Mix Columns
0FD68591 0AFAC4BC F4C9D7ED 64E96B07
Round[6] After Inverse Sub Bytes
FB4A67AC A3148878 BA120D53 8CEB0538
Round[6] After Inverse Shift Rows
FBEB0D78 A34A0553 BA146738 8C1288AC
Round[5] After Add RoundKey
4E423FF2 8532A314 22254511 A37EF11F
Round[5] After Mix Columns
1ADDF2F4 68934EB5 56C8975A E154D553
Round[5] After Inverse Sub Bytes
43C904BA F722B6D2 B9B18546 E0FDB550
Round[5] After Inverse Shift Rows
43FD85D2 F7C9B546 B9220450 E0B1B6BA
Round[4] After Add RoundKey
9667696A AC3A7C51 47CB4618 3E3F082C
Round[4] After Mix Columns
9D6C9D9E E2155F13 58B3E6DF F20B8E52
Round[4] After Inverse Sub Bytes
75B875DF 3B2F8482 5E4BF5EF 049EE648
Round[4] After Inverse Shift Rows
759EF582 3BB8E6EF 5E2F7548 044B84DF
Round[3] After Add RoundKey
DD2E6998 A8697222 E066F126 B316DF45
Round[3] After Mix Columns
D45C64EE 011DE26F 5CA7EF45 95148739
Round[3] After Inverse Sub Bytes
19A78C99 09DE3B06 A7896168 AD9BEA5B
Round[3] After Inverse Shift Rows
199B6106 09A7EA68 A7DE8C5B AD893B99
Round[2] After Add RoundKey
82383517 87CECFC7 02C40704 8DEEC747
Round[2] After Mix Columns
33AAAFAE 51979B1C 36C3A292 C29455E0
Round[2] After Inverse Sub Bytes
66621BBE 7085E8C4 24331A74 A8E7EDA0
Round[2] After Inverse Shift Rows
66E71AC4 7062ED74 24851BA0 A833E8BE
Round[1] After Add RoundKey
79D236C3 4B03E5A3 091D0B03 A127374A
Round[1] After Mix Columns
8BDD7870 2B1C99A0 D5B5EF93 BACAC14A
Round[1] After Inverse Sub Bytes
CEC9C1D0 0BC4F947 B5D26122 C010DD5C
Round[1] After Inverse Shift Rows
CE106147 0BC9DD22 B5C4C15C C0D2F9D0
Round[0] After Add Round Key
AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
Round[14] Input to Inverse Cipher
B6ED21B9 9CA6F4F9 F153E7B1 BEAFED1D
Round[14] After Add Round Key
48A5B168 7ABE79F2 F53E14F5 CEC38E03
Round[14] After Inverse Sub Bytes
D42956F7 BD5AAF04 77D19B77 EC33E6D5
Round[14] After Inverse Shift Rows
D4339B04 BD29E677 775A56D5 ECD1AFF7
Round[13] After Add RoundKey
1EC931E7 59FC7D43 ED853C1B 51C1B6FA
Round[13] After Mix Columns
1E9333BF B700BE92 55A31AA3 BDA5F93D
Round[13] After Inverse Sub Bytes
E92266F4 20525A74 ED714371 CD29698B
Round[13] After Inverse Shift Rows
E9294374 20226971 ED52668B CD715AF4
Round[12] After Add RoundKey
9DB504DF 387274AB 0F2718C4 B970CAAE
Round[12] After Mix Columns
B555D1C2 D666AB8E 16EDF2FD 55F86767
Round[12] After Inverse Sub Bytes
D2ED51A8 4AD30EE6 FF530421 EDE10A0A
Round[12] After Inverse Shift Rows
D2E104E6 4AED0A21 FFD3510A ED530EA8
Round[11] After Add RoundKey
8A67CEBB 64C23BF6 81D9A0F0 CA9C7D6B
Round[11] After Mix Columns
74471BB0 4AE5C307 FDC7CCFE FAC2CDB5
Round[11] After Inverse Sub Bytes
CA1644FC 5C2A3338 2131270C 14A880D2
Round[11] After Inverse Shift Rows
CAA82738 5C16800C 212A44D2 143133FC
Round[10] After Add RoundKey
14BB4E5F 30DADA7D DB0F2747 8245DDE9
Round[10] After Mix Columns
1BCE264D 6963195E D607593C 5AC2F893
Round[10] After Inverse Sub Bytes
44EC2365 E4008E9D 4A38156D 46A8E122
Round[10] After Inverse Shift Rows
44A8159D E4ECE16D 4A002322 46388E65
Round[9] After Add RoundKey
8CBCF799 92451AE7 1A25E30F 1FFD0C5C
Round[9] After Mix Columns
832644BF 50248CD2 BC0BF89C D9E3B53D
Round[9] After Inverse Sub Bytes
412386F4 6CA6F07F 789EE11C E54DD28B
Round[9] After Inverse Shift Rows
414DE17F 6C23D21C 78A6868B E59EF0F4
Round[8] After Add RoundKey
294D9AD3 DEFCE10A EE4FBF6F 89CF7D74
Round[8] After Mix Columns
45E8AC2C BDE80B97 3CE08F22 F96B934E
Round[8] After Inverse Sub Bytes
68C8AA42 CDC89E85 6DA07394 690522B6
Round[8] After Inverse Shift Rows
68057385 CDC82294 6DC8AAB6 69A09E42
Round[7] After Add RoundKey
F0C0CC4C 73753B1A 4B449111 6040DC56
Round[7] After Mix Columns
2799606E 404A466B 8B215471 6BB698EF
Round[7] After Inverse Sub Bytes
3DF99045 725C9805 CE7BFD2C 0579E261
Round[7] After Inverse Shift Rows
3D79FD05 72F9E22C CE5C9061 057B9845
Round[6] After Add RoundKey
BC557CA8 A826AA96 EA6A9A93 FFC32C21
Round[6] After Mix Columns
96102C97 F2868F49 87F5FE05 4401F581
Round[6] After Inverse Sub Bytes
357C4285 04DC73A4 EA770C36 86097791
Round[6] After Inverse Shift Rows
35090CA4 047C7736 EADC4291 86777385
Round[5] After Add RoundKey
80A03E2E 2204D171 72ED60B8 A91B0A36
Round[5] After Mix Columns
A5227BCC 55A0B1C2 56EACA31 FE1F5A35
Round[5] After Inverse Sub Bytes
29940327 ED4756A8 B9BB102E 0CCB46D9
Round[5] After Inverse Shift Rows
29CB10A8 ED94462E B94703D9 0CBB5627
Round[4] After Add RoundKey
FC51FC10 B6678F39 47AE4191 D235E8B1
Round[4] After Mix Columns
C27040B3 99BD6E2D 7C7D0830 D68B8B68
Round[4] After Inverse Sub Bytes
A8D0724B F9CD45FA 0113BF08 4ACECEF7
Round[4] After Inverse Shift Rows
A8CEBFFA F9D0CE08 01CD72F7 4A13454B
Round[3] After Add RoundKey
007E23E0 6A015AC5 BF84F699 FD4E1ED1
Round[3] After Mix Columns
52A81057 699FAAA8 34D6D563 90158B72
Round[3] After Inverse Sub Bytes
486F7CDA E46E626F 284AB500 962FCE1E
Round[3] After Inverse Shift Rows
482FB56F E46FCE00 286E7C1E 964A62DA
Round[2] After Add RoundKey
D38CE17E 6A06EBAF 8D74F741 B62D9E04
Round[2] After Mix Columns
3F299640 F32622DF 96BC7217 32FD18D6
Round[2] After Inverse Sub Bytes
254C3572 7E2394EF 35781E87 A121344A
Round[2] After Inverse Shift Rows
25211EEF 7E4C3487 3523354A A1789472
Round[1] After Add RoundKey
3A1432E8 452D3C50 18BB25E9 A86C4B86
Round[1] After Mix Columns
5390A89F 4EC43FB1 8BF56879 DBE62A1E
Round[1] After Inverse Sub Bytes
50966F6E B6882556 CE77F7AF 9FF595E9
Round[1] After Inverse Shift Rows
50F5F756 B69695AF CE886FE9 9F77256E
Round[0] After Add Round Key
30C81C46 A35CE411 E5FBC119 1A0A52EF
Round[14] Input to Inverse Cipher
23304B7A 39F9F3FF 067D8D8F 9E24ECC7
Round[14] After Add Round Key
DD78DBAB DFE17EF4 02107ECB EE488FD9
Round[14] After Inverse Sub Bytes
C9C19F0E EFE08ABA 6A7C8A59 99D473E5
Round[14] After Inverse Shift Rows
C9D48ABA EFC17359 6AE09FE5 997C8A0E
Round[13] After Add RoundKey
032E2059 0B14E86D F03FF52B 246C9303
Round[13] After Mix Columns
17379CE8 B22E7E78 F879DF4F 1C6C00A8
Round[13] After Inverse Sub Bytes
87B21CC8 3EC38AC1 E1AFEF92 C4B8526F
Round[13] After Inverse Shift Rows
87B8EFC1 3EB25292 E1C31C6F C4AF8AC8
Round[12] After Add RoundKey
F324A86A 26E24F48 03B66220 B0AE1A92
Round[12] After Mix Columns
8CB9FDDD 8BBC7F8B E3657706 5867C56C
Round[12] After Inverse Sub Bytes
F0DB21C9 CE786BCE 4DBC02A5 5E0A07B8
Round[12] After Inverse Shift Rows
F00A02CE CEDB07A5 4D7821B8 5EBC6BC9
Round[11] After Add RoundKey
A88CC893 E0F43672 3372D042 7973180A
Round[11] After Mix Columns
D1D24F33 5BA32D85 01FC5F71 2A827BCB
Round[11] After Inverse Sub Bytes
517F9266 5771FA67 0955842C 95110359
Round[11] After Inverse Shift Rows
51118467 577F032C 09719259 9555FA66
Round[10] After Add RoundKey
8F02ED00 3BB3595D F354F1CC 03211473
Round[10] After Mix Columns
5082F240 23694284 8875A5C2 4043DD9B
Round[10] After Inverse Sub Bytes
6C110472 32E4F64F 973F29A8 7264C9E8
Round[10] After Inverse Shift Rows
6C64294F 3211C9A8 97E404E8 723FF672
Round[9] After Add RoundKey
A470CB4B 44B83222 C7C1C4C5 2BFA744B
Round[9] After Mix Columns
7233B5A0 A9241C7D F8E4F5EE 2AD0B2A6
Round[9] After Inverse Sub Bytes
1E66D247 B7A6C413 E1AE7799 95603EC5
Round[9] After Inverse Shift Rows
1E607713 B7663E99 E1A6D2C5 95AEC447
Round[8] After Add RoundKey
76600CBF 05B90D8F 774FEB21 F9FF49C7
Round[8] After Mix Columns
5313789D 93C7E78D 629C010D A7CC1CFF
Round[8] After Inverse Sub Bytes
5082C175 2231B0B4 AB1C09F3 8927C47D
Round[8] After Inverse Shift Rows
502709B4 2282C4F3 AB31C17D 891CB075
Round[7] After Add RoundKey
C8E2B67D 9C3FDD7D 8DBDFADA 80FCF261
Round[7] After Mix Columns
D7A870EE C5E882AC BA24ED63 7D74CA2C
Round[7] After Inverse Sub Bytes
0D6FD099 07C811AA C0A65300 13CA1042
Round[7] After Inverse Shift Rows
0DCA53AA 076F1000 C0C8D042 13A61199
Round[6] After Add RoundKey
8CE6D207 DDB058BA E4FEDAB0 E91EA5FD
Round[6] After Mix Columns
0B173093 BEC83EC7 F5482BE6 97729ED4
Round[6] After Inverse Sub Bytes
9E870822 5AB1D131 77D40BF5 851EDF19
Round[6] After Inverse Shift Rows
9E1E0B31 5A87DFF5 77B10819 85D4D122
Round[5] After Add RoundKey
2BB739BB 7CFF79B2 EF802A30 AAB8A891
Round[5] After Mix Columns
AE6E805E 4BF9DE24 F8C9D793 EE54BA2B
Round[5] After Inverse Sub Bytes
BE453A9D CC699CA6 E1120D22 99FDC00B
Round[5] After Inverse Shift Rows
BEFD0DA6 CC45C022 E1693A0B 99129C9D
Round[4] After Add RoundKey
6B67E11E 97B60935 1F807843 479C220B
Round[4] After Mix Columns
47A53021 6E1CCAA5 4EB97A29 46B2DCDA
Round[4] After Inverse Sub Bytes
1629087B 45C41029 B6DBBD4C 983E937A
Round[4] After Inverse Shift Rows
163EBD29 4529934C B6C4087A 98DB107B
Round[3] After Add RoundKey
BE8E2133 D6F80781 088D8C14 2F864BE1
Round[3] After Mix Columns
BD2066D9 7C7DE64F CA28748B F69B94FA
Round[3] After Inverse Sub Bytes
CD54D3E5 0113F592 10EECACE D6E8E714
Round[3] After Inverse Shift Rows
CDE8CA92 0154E7CE 1013D314 D6EEF5E5
Round[2] After Add RoundKey
564B9E83 8F3DC261 B509584B F689093B
Round[2] After Mix Columns
61F7A93F 462A2954 EF18471F CA7FAF57
Round[2] After Inverse Sub Bytes
D826B725 98954CFD 613416CB 106B1BDA
Round[2] After Inverse Shift Rows
D86B16FD 98261BCB 6195B7DA 10344C25
Round[1] After Add RoundKey
C75E3AFA A347131C 4C0DA779 192093D1
Round[1] After Mix Columns
9097DF81 746A09FC 44828AD3 FB3A873D
Round[1] After Inverse Sub Bytes
9685EF91 CA584055 8611CFA9 63A2EA8B
Round[1] After Inverse Shift Rows
96A2CF55 CA85EAA9 8658EF8B 63114091
Round[0] After Add Round Key
F69F2445 DF4F9B17 AD2B417B E66C3710