// EigenVV2x2.cpp (c) Wednesday, September 3, 2025
// by James Pate Williams, Jr., BA, BS, MSwE, PhD
// Solution to Exercise 1.11 in "Quantum Chemistry
// an Introduction to Advanced Electronic Structure
// Theory (c) 1996 by Attila Szabo and Neil S. Ostlund
#include "pch.h"
#include "framework.h"
#include "EigenVV2x2.h"
#define MAX_LOADSTRING 100
// Global Variables:
HINSTANCE hInst; // current instance
WCHAR szTitle[MAX_LOADSTRING]; // The title bar text
WCHAR szWindowClass[MAX_LOADSTRING]; // the main window class name
std::wstring text; // output wide string
// Forward declarations of functions included in this code module:
ATOM MyRegisterClass(HINSTANCE hInstance);
BOOL InitInstance(HINSTANCE, int);
LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);
INT_PTR CALLBACK About(HWND, UINT, WPARAM, LPARAM);
int APIENTRY wWinMain(_In_ HINSTANCE hInstance,
_In_opt_ HINSTANCE hPrevInstance,
_In_ LPWSTR lpCmdLine,
_In_ int nCmdShow)
{
UNREFERENCED_PARAMETER(hPrevInstance);
UNREFERENCED_PARAMETER(lpCmdLine);
// TODO: Place code here.
// Initialize global strings
LoadStringW(hInstance, IDS_APP_TITLE, szTitle, MAX_LOADSTRING);
LoadStringW(hInstance, IDC_EIGENVV2X2, szWindowClass, MAX_LOADSTRING);
MyRegisterClass(hInstance);
// Perform application initialization:
if (!InitInstance (hInstance, nCmdShow))
{
return FALSE;
}
HACCEL hAccelTable = LoadAccelerators(hInstance, MAKEINTRESOURCE(IDC_EIGENVV2X2));
MSG msg;
// Main message loop:
while (GetMessage(&msg, nullptr, 0, 0))
{
if (!TranslateAccelerator(msg.hwnd, hAccelTable, &msg))
{
TranslateMessage(&msg);
DispatchMessage(&msg);
}
}
return (int) msg.wParam;
}
//
// FUNCTION: MyRegisterClass()
//
// PURPOSE: Registers the window class.
//
ATOM MyRegisterClass(HINSTANCE hInstance)
{
WNDCLASSEXW wcex;
wcex.cbSize = sizeof(WNDCLASSEX);
wcex.style = CS_HREDRAW | CS_VREDRAW;
wcex.lpfnWndProc = WndProc;
wcex.cbClsExtra = 0;
wcex.cbWndExtra = 0;
wcex.hInstance = hInstance;
wcex.hIcon = LoadIcon(hInstance, MAKEINTRESOURCE(IDI_EIGENVV2X2));
wcex.hCursor = LoadCursor(nullptr, IDC_ARROW);
wcex.hbrBackground = (HBRUSH)(COLOR_WINDOW+1);
wcex.lpszMenuName = MAKEINTRESOURCEW(IDC_EIGENVV2X2);
wcex.lpszClassName = szWindowClass;
wcex.hIconSm = LoadIcon(wcex.hInstance, MAKEINTRESOURCE(IDI_SMALL));
return RegisterClassExW(&wcex);
}
//
// FUNCTION: InitInstance(HINSTANCE, int)
//
// PURPOSE: Saves instance handle and creates main window
//
// COMMENTS:
//
// In this function, we save the instance handle in a global variable and
// create and display the main program window.
//
BOOL InitInstance(HINSTANCE hInstance, int nCmdShow)
{
hInst = hInstance; // Store instance handle in our global variable
HWND hWnd = CreateWindowW(szWindowClass, szTitle, WS_OVERLAPPEDWINDOW,
CW_USEDEFAULT, 0, CW_USEDEFAULT, 0, nullptr, nullptr, hInstance, nullptr);
if (!hWnd)
{
return FALSE;
}
ShowWindow(hWnd, nCmdShow);
UpdateWindow(hWnd);
return TRUE;
}
#define IDC_STATIC1 1000
#define IDC_STATIC2 1010
#define IDC_STATIC3 1020
#define IDC_STATIC4 1030
#define IDC_EDIT_A11 2000
#define IDC_EDIT_A12 2010
#define IDC_EDIT_A21 2020
#define IDC_EDIT_A22 2030
#define IDC_EDIT_MULTILINE 3000
#define IDC_BUTTON_COMPUTE 4000
#define IDC_BUTTON_CANCEL 4010
//
// FUNCTION: WndProc(HWND, UINT, WPARAM, LPARAM)
//
// PURPOSE: Processes messages for the main window.
//
// WM_COMMAND - process the application menu
// WM_PAINT - Paint the main window
// WM_DESTROY - post a quit message and return
//
//
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
static HFONT hFont = { };
static HWND hEditMultiline = { };
static HWND hEditA11 = { };
static HWND hEditA12 = { };
static HWND hEditA21 = { };
static HWND hEditA22 = { };
switch (message)
{
case WM_CREATE:
{
hFont = CreateFont(16, 0, 0, 0, FW_NORMAL, FALSE, FALSE, FALSE,
ANSI_CHARSET, OUT_DEFAULT_PRECIS, CLIP_DEFAULT_PRECIS,
DEFAULT_QUALITY, DEFAULT_PITCH | FF_SWISS, L"Courier New Bold");
CreateWindowEx(0, L"STATIC", L"A[1][1]:", WS_CHILD | WS_VISIBLE,
10, 10, 80, 20, hWnd, (HMENU)IDC_STATIC1, hInst, NULL);
CreateWindowEx(0, L"STATIC", L"A[1][2]:", WS_CHILD | WS_VISIBLE,
10, 40, 80, 20, hWnd, (HMENU)IDC_STATIC2, hInst, NULL);
CreateWindowEx(0, L"STATIC", L"A[2][1]:", WS_CHILD | WS_VISIBLE,
10, 70, 80, 20, hWnd, (HMENU)IDC_STATIC3, hInst, NULL);
CreateWindowEx(0, L"STATIC", L"A[2][2]:", WS_CHILD | WS_VISIBLE,
10, 100, 80, 20, hWnd, (HMENU)IDC_STATIC4, hInst, NULL);
hEditA11 = CreateWindowEx(0, L"EDIT", NULL, WS_CHILD | WS_VISIBLE | WS_BORDER,
100, 10, 200, 20, hWnd, (HMENU)IDC_EDIT_A11, hInst, NULL);
hEditA12 = CreateWindowEx(0, L"EDIT", NULL, WS_CHILD | WS_VISIBLE | WS_BORDER,
100, 40, 200, 20, hWnd, (HMENU)IDC_EDIT_A12, hInst, NULL);
hEditA21 = CreateWindowEx(0, L"EDIT", NULL, WS_CHILD | WS_VISIBLE | WS_BORDER,
100, 70, 200, 20, hWnd, (HMENU)IDC_EDIT_A21, hInst, NULL);
hEditA22 = CreateWindowEx(0, L"EDIT", NULL, WS_CHILD | WS_VISIBLE | WS_BORDER,
100, 100, 200, 20, hWnd, (HMENU)IDC_EDIT_A22, hInst, NULL);
hEditMultiline = CreateWindowEx(
WS_EX_CLIENTEDGE, // Extended style for sunken border
TEXT("EDIT"), // Class name
TEXT(""), // Initial text (can be blank)
WS_CHILD | WS_VISIBLE | WS_VSCROLL | ES_AUTOHSCROLL |
ES_LEFT | ES_MULTILINE | ES_AUTOVSCROLL | WS_HSCROLL | WS_VSCROLL,
310, 10, 300, 300, // Position and size
hWnd, // Parent window handle
(HMENU)IDC_EDIT_MULTILINE, // Unique control ID
hInst, // Application instance
NULL // Extra parameter
);
CreateWindowEx(0, L"BUTTON", L"Compute", WS_CHILD | WS_VISIBLE | BS_PUSHBUTTON,
10, 130, 80, 30, hWnd, (HMENU)IDC_BUTTON_COMPUTE, hInst, NULL);
CreateWindowEx(0, L"BUTTON", L"Cancel", WS_CHILD | WS_VISIBLE | BS_PUSHBUTTON,
220, 130, 80, 30, hWnd, (HMENU)IDC_BUTTON_CANCEL, hInst, NULL);
SendMessage(hEditMultiline, WM_SETFONT, (WPARAM)hFont, TRUE);
SetDlgItemText(hWnd, IDC_EDIT_A11, L"3");
SetDlgItemText(hWnd, IDC_EDIT_A12, L"1");
SetDlgItemText(hWnd, IDC_EDIT_A21, L"1");
SetDlgItemText(hWnd, IDC_EDIT_A22, L"3");
}
break;
case WM_COMMAND:
{
int wmId = LOWORD(wParam);
// Parse the menu selections:
switch (wmId)
{
case IDM_ABOUT:
DialogBox(hInst, MAKEINTRESOURCE(IDD_ABOUTBOX), hWnd, About);
break;
case IDC_BUTTON_COMPUTE:
{
WCHAR line[128] = L"";
text = L"";
// eigenvalues
std::vector<double> omega(3);
// matrix
std::vector<std::vector<double>> A(3,
std::vector<double>(3));
std::vector<std::vector<double>> B(3,
std::vector<double>(3));
// eigenvectors
std::vector<std::vector<double>> c(3,
std::vector<double>(3));
GetWindowText(hEditA11, line, 128);
std::wstring A11Str(line);
A[1][1] = std::stod(A11Str);
GetWindowText(hEditA12, line, 128);
std::wstring A12Str(line);
A[1][2] = std::stod(A12Str);
GetWindowText(hEditA21, line, 128);
std::wstring A21Str(line);
A[2][1] = std::stod(A21Str);
GetWindowText(hEditA22, line, 128);
std::wstring A22Str(line);
A[2][2] = std::stod(A22Str);
double term1 = A[1][1] + A[2][2];
double term2 = pow(A[2][2] - A[1][1], 2.0);
double term3 = 4.0 * A[1][2] * A[2][1];
// compute eigenvalues
omega[1] = 0.5 * (term1 - sqrt(term2 + term3));
omega[2] = 0.5 * (term1 + sqrt(term2 + term3));
swprintf_s(line, L"Eigenvalues:\r\n\r\n");
text += std::wstring(line);
swprintf_s(line, L"omega 1 = %13.10lf\r\n", omega[1]);
text += std::wstring(line);
swprintf_s(line, L"omega 2 = %13.10lf\r\n\r\n", omega[2]);
text += std::wstring(line);
// compute eigenvalues using a unitary transformation
// matrix A must be symmetric
double theta0 = 0.0;
if (A[1][1] == A[2][2])
{
theta0 = 0.5 * acos(0.0);
}
else
{
theta0 = 0.5 * atan(2.0 * A[1][2] /
(A[1][1] - A[2][2]));
}
// compute the eigenvalues
omega[1] = A[1][1] * pow(cos(theta0), 2.0) +
A[2][2] * pow(sin(theta0), 2.0) +
A[1][2] * sin(2.0 * theta0);
omega[2] = A[1][1] * pow(cos(theta0), 2.0) +
A[2][2] * pow(sin(theta0), 2.0) -
A[1][2] * sin(2.0 * theta0);
swprintf_s(line, L"Eigenvalues:\r\n\r\n");
text += std::wstring(line);
swprintf_s(line, L"omega 1 = %13.10lf\r\n", omega[1]);
text += std::wstring(line);
swprintf_s(line, L"omega 2 = %13.10lf\r\n\r\n", omega[2]);
text += std::wstring(line);
// compute eigenvectors
c[1][1] = cos(theta0);
c[1][2] = sin(theta0);
c[2][1] = sin(theta0);
c[2][2] = -cos(theta0);
swprintf_s(line, L"Eigenvectors:\r\n\r\n");
text += std::wstring(line);
swprintf_s(line, L"c 11 = %13.10lf\r\n", c[1][1]);
text += std::wstring(line);
swprintf_s(line, L"c 12 = %13.10lf\r\n", c[1][2]);
text += std::wstring(line);
swprintf_s(line, L"c 21 = %13.10lf\r\n", c[2][1]);
text += std::wstring(line);
swprintf_s(line, L"c 22 = %13.10lf\r\n", c[2][2]);
text += std::wstring(line);
SetWindowText(hEditMultiline, text.c_str());
break;
}
case IDC_BUTTON_CANCEL:
{
PostQuitMessage(0);
break;
}
break;
case IDM_EXIT:
DestroyWindow(hWnd);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
}
break;
case WM_PAINT:
{
PAINTSTRUCT ps;
HDC hdc = BeginPaint(hWnd, &ps);
// TODO: Add any drawing code that uses hdc here...
EndPaint(hWnd, &ps);
}
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
}
// Message handler for about box.
INT_PTR CALLBACK About(HWND hDlg, UINT message, WPARAM wParam, LPARAM lParam)
{
UNREFERENCED_PARAMETER(lParam);
switch (message)
{
case WM_INITDIALOG:
return (INT_PTR)TRUE;
case WM_COMMAND:
if (LOWORD(wParam) == IDOK || LOWORD(wParam) == IDCANCEL)
{
EndDialog(hDlg, LOWORD(wParam));
return (INT_PTR)TRUE;
}
break;
}
return (INT_PTR)FALSE;
}
Category: Matrix Algebra
Blog Entry © Tuesday, September 2, 2025, by James Pate Williams, Jr. Testing of a Backpropagation Neural Network Function Approximator
Blog Entry © Friday, August 29, 2025, by James Pate Williams, Jr., Eigenvalue and Eigenvector Calculators and Linear System of Equations Solver
Blog Entry © Friday, August 22, 2025, by James Pate Williams, Jr. New Quantum Chemical Total Molecular Ground-State Energies for the Helium Hydride Cation (a Hetero Nuclear molecule) and the Hydrogen Molecule (a Homo Nuclear Molecule)
Blog Entry © Tuesday, August 19, 2025, by James Pate Williams, Jr., Continuation of Answers to the Exercises in Chapter 1 of Modern Quantum Chemistry an Introduction to Advanced Electronic Structure Theory by Attila Szabo and Neil S. Ostlund
Note: Later on, Tuesday, August 19, 2025, I added five C++ source code files.
#include <vector>
#include <random>
class DblLinearAlgebra
{
public:
static void DblPrintMatrix(
int m, int n, std::vector<std::vector<double>>& A);
static void DblAddition(
size_t m, size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C);
static void DblSubtraction(
size_t m, size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C);
static void DblMultiply(
size_t m, size_t n, size_t p,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C);
static void DblAnticommutator(
size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C);
static void DblCommutator(
size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C);
static double DblDeterminant(
int n, int row, int col,
std::vector<std::vector<double>>& A);
static bool DblGaussianElimination(
int m, int n, std::vector<std::vector<double>>& A,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot);
static bool DblGaussianFactor(
int n, std::vector<std::vector<double>>& M,
std::vector<size_t>& pivot);
static bool DblGaussianSolution(
int n, std::vector<std::vector<double>>& M,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot);
static bool DblSubstitution(
int n, std::vector<std::vector<double>>& M,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot);
static bool DblInverse(
int n, std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& A);
static void DblCharPolyAndAdjoint(
int n,
std::vector<std::vector<double>>& C,
std::vector<std::vector<double>>& I,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& adjoint,
std::vector<double>& a);
static void DblMatrixKernel(
int m, int n,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& X,
size_t& r);
static void DblMatrixImage(
int m, int n,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& N,
std::vector<std::vector<double>>& X,
int rank);
static void DblGenerateNonSingular(
double scale, double& determinant,
int n, unsigned int seed,
std::vector<std::vector<double>>& Mr);
};
#include "DblLinearAlgebra.h"
#include <iomanip>
#include <iostream>
void DblLinearAlgebra::DblPrintMatrix(
int m, int n, std::vector<std::vector<double>>& A)
{
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
std::cout << std::setprecision(6) << std::setw(9);
if (fabs(A[i][j]) > 1.0e-12)
{
std::cout << A[i][j] << ' ';
}
else
{
std::cout << 0 << ' ';
}
}
std::cout << std::endl;
}
}
void DblLinearAlgebra::DblAddition(
size_t m, size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
C[i][j] = A[i][j] + B[i][j];
}
}
}
void DblLinearAlgebra::DblSubtraction(
size_t m, size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
C[i][j] = A[i][j] - B[i][j];
}
}
}
void DblLinearAlgebra::DblMultiply(
size_t m, size_t n, size_t p,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
double sum = { 0 };
for (size_t k = 0; k < p; k++)
{
sum += A[i][k] * B[k][j];
}
C[i][j] = sum;
}
}
}
void DblLinearAlgebra::DblAnticommutator(
size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C)
{
std::vector<std::vector<double>> D(n,
std::vector<double>(n));
std::vector<std::vector<double>> E(n,
std::vector<double>(n));
DblMultiply(n, n, n, A, B, D);
DblMultiply(n, n, n, B, A, E);
DblAddition(n, n, D, E, C);
}
void DblLinearAlgebra::DblCommutator(
size_t n,
std::vector<std::vector<double>>& A,
std::vector<std::vector<double>>& B,
std::vector<std::vector<double>>& C)
{
std::vector<std::vector<double>> D(n,
std::vector<double>(n));
std::vector<std::vector<double>> E(n,
std::vector<double>(n));
DblMultiply(n, n, n, A, B, D);
DblMultiply(n, n, n, B, A, E);
DblSubtraction(n, n, D, E, C);
}
// https://www.geeksforgeeks.org/dsa/determinant-of-a-matrix/
double getDet(std::vector<std::vector<double>>& mat, int n) {
// Base case: if the matrix is 1x1
if (n == 1) {
return mat[0][0];
}
// Base case for 2x2 matrix
if (n == 2) {
return mat[0][0] * mat[1][1] -
mat[0][1] * mat[1][0];
}
// Recursive case for larger matrices
double res = 0;
for (int col = 0; col < n; ++col) {
// Create a submatrix by removing the first
// row and the current column
std::vector<std::vector<double>> sub(n - 1,
std::vector<double>(n - 1));
for (int i = 1; i < n; ++i) {
int subcol = 0;
for (int j = 0; j < n; ++j) {
// Skip the current column
if (j == col) continue;
// Fill the submatrix
sub[i - 1LL][subcol++] = mat[i][j];
}
}
// Cofactor expansion
int sign = (col % 2 == 0) ? 1 : -1;
res += sign * mat[0][col] * getDet(sub, n - 1);
}
return res;
}
double DblLinearAlgebra::DblDeterminant(
int n, int row, int col,
std::vector<std::vector<double>>& A)
{
return getDet(A, A.size());
}
bool DblLinearAlgebra::DblGaussianElimination(
int m, int n, std::vector<std::vector<double>>& M,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot)
{
bool failure = false;
std::vector<double> c(m);
b.resize(n);
x.resize(n);
for (size_t i = 0; i < m; i++)
c[i] = -1;
for (size_t j = 0; j < n; j++)
{
bool found = false;
size_t i = j;
while (i < n && !found)
{
if (M[i][j] != 0)
found = true;
else
i++;
}
if (!found)
{
failure = true;
break;
}
if (i > j)
{
for (size_t l = j; l < n; l++)
{
double t = M[i][l];
M[i][l] = M[j][l];
M[j][l] = t;
t = b[i];
b[i] = b[j];
b[j] = t;
}
}
double d = 1.0 / M[j][j];
for (size_t k = j + 1; k < n; k++)
c[k] = d * M[k][j];
for (size_t k = j + 1; k < n; k++)
{
for (size_t l = j + 1; l < n; l++)
M[k][l] = M[k][l] - c[k] * M[j][l];
b[k] = b[k] - c[k] * b[j];
}
}
for (long long i = (long long)n - 1; i >= 0; i--)
{
double sum = 0;
for (size_t j = i + 1; j < n; j++)
sum += M[i][j] * x[j];
x[i] = (b[i] - sum) / M[i][i];
}
return failure;
}
bool DblLinearAlgebra::DblGaussianFactor(
int n, std::vector<std::vector<double>>& M,
std::vector<size_t>& pivot)
{
// returns false if matrix is singular
std::vector<double> d(n);
double awikod, col_max, ratio, row_max, temp;
int flag = 1;
size_t i_star, itemp;
for (size_t i = 0; i < n; i++)
{
pivot[i] = i;
row_max = 0;
for (size_t j = 0; j < n; j++)
row_max = fmax(row_max, fabs(M[i][j]));
if (row_max == 0)
{
flag = 0;
row_max = 1.0;
}
d[i] = row_max;
}
if (n <= 1) return flag != 0;
// factorization
for (size_t k = 0; k < (size_t)(n - 1LL); k++)
{
// determine pivot row the row i_star
col_max = fabs(M[k][k]) / d[k];
i_star = k;
for (size_t i = k + 1; i < n; i++)
{
awikod = fabs(M[i][k]) / d[i];
if (awikod > col_max)
{
col_max = awikod;
i_star = i;
}
}
if (col_max == 0)
flag = 0;
else
{
if (i_star > k)
{
// make k the pivot row by
// interchanging with i_star
flag *= -1;
itemp = pivot[i_star];
pivot[i_star] = pivot[k];
pivot[k] = itemp;
temp = d[i_star];
d[i_star] = d[k];
d[k] = temp;
for (size_t j = 0; j < n; j++)
{
temp = M[i_star][j];
M[i_star][j] = M[k][j];
M[k][j] = temp;
}
}
// eliminate x[k]
for (size_t i = k + 1; i < n; i++)
{
M[i][k] /= M[k][k];
ratio = M[i][k];
for (size_t j = k + 1; j < n; j++)
M[i][j] -= ratio * M[k][j];
}
}
if (M[n - 1LL][n - 1LL] == 0) flag = 0;
}
if (flag == 0)
return false;
return true;
}
bool DblLinearAlgebra::DblGaussianSolution(
int n, std::vector<std::vector<double>>& M,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot)
{
if (!DblGaussianFactor(n, M, pivot))
return false;
return DblSubstitution(n, M, b, x, pivot);
}
bool DblLinearAlgebra::DblSubstitution(
int n, std::vector<std::vector<double>>& M,
std::vector<double>& b, std::vector<double>& x,
std::vector<size_t>& pivot)
{
double sum = 0.0;
size_t n1 = n - 1LL;
if (n == 1)
{
x[0] = b[0] / M[0][0];
return true;
}
// forward substitution
x[0] = b[pivot[0]];
for (size_t i = 1; i < n; i++)
{
double sum = 0.0;
for (size_t j = 0; j < i; j++)
sum += M[i][j] * x[j];
x[i] = b[pivot[i]] - sum;
}
// backward substitution
x[n1] /= M[n1][n1];
for (long long i = n - 2LL; i >= 0; i--)
{
double sum = 0.0;
for (size_t j = i + 1; j < n; j++)
sum += M[i][j] * x[j];
x[i] = (x[i] - sum) / M[i][i];
}
return true;
}
bool DblLinearAlgebra::DblInverse(
int n, std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& Mi)
{
std::vector<double> b(n);
std::vector<double> x(n);
std::vector<size_t> pivot(n);
std::vector<std::vector<double>> Mc(n,
std::vector<double>(n));
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
Mc[i][j] = M[i][j];
}
}
if (!DblGaussianFactor(n, Mc, pivot))
return false;
for (size_t i = 0; i < n; i++)
{
b[i] = 0;
}
for (size_t i = 0; i < n; i++)
{
b[i] = 1;
if (!DblSubstitution(n, Mc, b, x, pivot))
return false;
b[i] = 0;
for (size_t j = 0; j < n; j++)
Mi[j][i] = x[j];
}
return true;
}
void DblLinearAlgebra::DblCharPolyAndAdjoint(
int n,
std::vector<std::vector<double>>& C,
std::vector<std::vector<double>>& I,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& adjoint,
std::vector<double>& a)
{
C.resize(n, std::vector<double>(n));
I.resize(n, std::vector<double>(n));
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
C[i][j] = I[i][j] = 0;
}
for (size_t i = 0; i < n; i++)
C[i][i] = I[i][i] = 1;
a[0] = 1;
for (size_t i = 1; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
for (size_t k = 0; k < n; k++)
{
double sum = 0.0;
for (size_t l = 0; l < n; l++)
sum += M[j][l] * C[l][k];
C[j][k] = sum;
}
}
double tr = 0.0;
for (size_t j = 0; j < n; j++)
tr += C[j][j];
a[i] = -tr / i;
for (size_t j = 0; j < n; j++)
{
for (size_t k = 0; k < n; k++)
C[j][k] += a[i] * I[j][k];
}
}
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
double sum = 0.0;
for (size_t k = 0; k < n; k++)
sum += M[i][k] * C[k][j];
C[i][j] = sum;
}
}
double trace = 0.0;
for (size_t i = 0; i < n; i++)
trace += C[i][i];
trace /= n;
a[n - 1LL] = -trace;
double factor = 1.0;
if ((n - 1) % 2 != 0)
factor = -1.0;
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
adjoint[i][j] = factor * C[i][j];
}
}
void DblLinearAlgebra::DblMatrixKernel(
int m, int n,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& X,
size_t& r)
{
double D = 0.0;
std::vector <int> c(m);
std::vector <int> d(n);
r = 0;
for (size_t i = 0; i < m; i++)
c[i] = -1;
size_t j, k = 1;
Step2:
for (j = 0; j < m; j++)
{
if (M[j][k] != 0 && c[j] == -1)
break;
}
if (j == m)
{
r++;
d[k] = 0;
goto Step4;
}
D = -1.0 / M[j][k];
M[j][k] = -1;
for (size_t s = k + 1; s < n; s++)
{
M[j][s] = D * M[j][s];
for (size_t i = 0; i < m; i++)
{
if (i != j)
{
D = M[i][k];
M[i][k] = 0;
}
}
}
for (size_t s = k + 1; s < n; s++)
{
for (size_t i = 0; i < m; i++)
{
M[i][s] += D * M[j][s];
}
}
c[j] = (int)k;
d[k] = (int)j;
Step4:
if (k < n - 1)
{
k++;
goto Step2;
}
X.resize(n, std::vector<double>(n));
if (r != 0)
{
for (k = 0; k < n; k++)
{
if (d[k] == 0)
{
for (size_t i = 0; i < n; i++)
{
if (d[i] > 0)
X[k][i] = M[d[i]][k];
else if (i == k)
X[k][i] = 1;
else
X[k][i] = 0;
}
}
}
}
}
void DblLinearAlgebra::DblMatrixImage(
int m, int n,
std::vector<std::vector<double>>& M,
std::vector<std::vector<double>>& N,
std::vector<std::vector<double>>& X,
int rank)
{
double D = 0.0;
size_t r = 0;
std::vector<std::vector<double>> copyM(
m, std::vector<double>(n));
std::vector <int> c(m);
std::vector <int> d(n);
for (size_t i = 0; i < m; i++)
c[i] = -1;
size_t j = 0, k = 1;
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
N[i][j] = copyM[i][j] = M[i][j];
}
}
Step2:
for (size_t j = 0; j < m; j++)
{
if (copyM[j][k] != 0 && c[j] == -1)
break;
}
if (j == m)
{
r++;
d[k] = 0;
goto Step4;
}
D = -1.0 / copyM[j][k];
copyM[j][k] = -1;
for (size_t s = k + 1; s < n; s++)
{
copyM[j][s] = D * copyM[j][s];
for (size_t i = 0; i < m; i++)
{
if (i != j)
{
D = copyM[i][k];
copyM[i][k] = 0;
}
}
}
for (size_t s = k + 1; s < n; s++)
{
for (size_t i = 0; i < m; i++)
{
copyM[i][s] += D * copyM[j][s];
}
}
c[j] = (int)k;
d[k] = (int)j;
Step4:
if (k < (size_t)(n - 1LL))
{
k++;
goto Step2;
}
rank = (int)(n - r) ;
for (j = 0; j < m; j++)
{
if (c[j] != 0)
{
for (size_t i = 0; i < m; i++)
{
N[i][c[j]] = M[i][c[j]];
}
}
}
}
void DblLinearAlgebra::DblGenerateNonSingular(
double scale, double& determinant,
int n, unsigned int seed,
std::vector<std::vector<double>>& Mr)
{
bool failure = false;
std::mt19937 rng(seed);
std::uniform_real_distribution<double> dist(0.0, 1.0);
while (true)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
Mr[i][j] = scale * dist(rng);
}
}
determinant = DblDeterminant(n, 0, 0, Mr);
failure = determinant == 0;
if (!failure)
return;
}
}
#include <complex>
#include <vector>
class CmpLinearAlgebra
{
public:
static void CmpPrintMatrix(
int m, int n,
std::vector<std::vector<std::complex<double>>>& Ac);
static void CmpAddition(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C);
static void CmpSubtraction(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C);
static void CmpMultiply(
size_t m, size_t n, size_t p,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C);
static void CmpAnticommutator(
size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C);
static void CmpCommutator(
size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C);
static std::complex<double> CmpDeterminant(
int n,
std::vector<std::vector<std::complex<double>>>& Ac);
static void CmpAdjoint(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& Ac,
std::vector<std::vector<std::complex<double>>>& Ad);
static bool CmpGaussianElimination(
int m, int n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot);
static bool CmpGaussianFactor(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<size_t>& pivot);
static bool CmpGaussianSolution(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot);
static bool CmpSubstitution(
int m, int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot);
static bool CmpInverse(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& Mi);
static void CmpCharPolyAndAdjoint(
int n,
std::vector<std::vector<std::complex<double>>>& C,
std::vector<std::vector<std::complex<double>>>& I,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& adjoint,
std::vector<std::complex<double>>& a);
static void CmpMatrixKernel(
int m, int n,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& X,
size_t& r);
static void CmpMatrixImage(
int m, int n,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& N,
std::vector<std::vector<std::complex<double>>>& X,
int rank);
static void CmpGenerateNonSingular(
double scale, std::complex<double>& determinant,
int n, unsigned int seed,
std::vector<std::vector<std::complex<double>>>& Mc);
};
#include "CmpLinearAlgebra.h"
#include <iomanip>
#include <iostream>
#include <random>
void CmpLinearAlgebra::CmpPrintMatrix(
int m, int n,
std::vector<std::vector<std::complex<double>>>& Ac)
{
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (Ac[i][j]._Val[0] >= 0)
std::cout << '+';
else
std::cout << '-';
std::cout << std::setprecision(6) << std::setw(9);
if (fabs(Ac[i][j]._Val[0]) > 1.0e-12)
{
std::cout << fabs(Ac[i][j]._Val[0]) << ' ';
}
else
{
std::cout << 0 << ' ';
}
if (Ac[i][j]._Val[1] >= 0)
std::cout << '+';
else
std::cout << '-';
std::cout << std::setprecision(6) << std::setw(9);
if (fabs(Ac[i][j]._Val[1]) > 1.0e-12)
{
std::cout << fabs(Ac[i][j]._Val[1]) << "i\t";
}
else
{
std::cout << 0 << "i\t";
}
}
std::cout << std::endl;
}
}
void CmpLinearAlgebra::CmpAddition(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
C[i][j] = A[i][j] + B[i][j];
}
}
}
void CmpLinearAlgebra::CmpSubtraction(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
C[i][j] = A[i][j] - B[i][j];
}
}
}
void CmpLinearAlgebra::CmpMultiply(
size_t m, size_t n, size_t p,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
std::complex<double> sum = 0;
for (size_t k = 0; k < p; k++)
{
sum += A[i][k] * B[k][j];
}
C[i][j] = sum;
}
}
}
void CmpLinearAlgebra::CmpAnticommutator(
size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C)
{
std::vector<std::vector<std::complex<double>>> D(n,
std::vector<std::complex<double>>(n));
std::vector<std::vector<std::complex<double>>> E(n,
std::vector<std::complex<double>>(n));
CmpMultiply(n, n, n, A, B, D);
CmpMultiply(n, n, n, B, A, E);
CmpAddition(n, n, D, E, C);
}
void CmpLinearAlgebra::CmpCommutator(
size_t n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::vector<std::complex<double>>>& B,
std::vector<std::vector<std::complex<double>>>& C)
{
std::vector<std::vector<std::complex<double>>> D(n,
std::vector<std::complex<double>>(n));
std::vector<std::vector<std::complex<double>>> E(n,
std::vector<std::complex<double>>(n));
CmpMultiply(n, n, n, A, B, D);
CmpMultiply(n, n, n, B, A, E);
CmpSubtraction(n, n, D, E, C);
}
void CmpLinearAlgebra::CmpAdjoint(
size_t m, size_t n,
std::vector<std::vector<std::complex<double>>>& Ac,
std::vector<std::vector<std::complex<double>>>& Ad)
{
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
Ad[j][i] = std::conj(Ac[i][j]);
}
}
}
// https://www.geeksforgeeks.org/dsa/determinant-of-a-matrix/
std::complex<double> getDet(
std::vector<std::vector<std::complex<double>>>& mat, int n) {
// Base case: if the matrix is 1x1
if (n == 1) {
return mat[0][0];
}
// Base case for 2x2 matrix
if (n == 2) {
return mat[0][0] * mat[1][1] -
mat[0][1] * mat[1][0];
}
// Recursive case for larger matrices
std::complex<double> res = 0;
for (int col = 0; col < n; ++col) {
// Create a submatrix by removing the first
// row and the current column
std::vector<std::vector<std::complex<double>>> sub(n - 1,
std::vector<std::complex<double>>(n - 1));
for (int i = 1; i < n; ++i) {
int subcol = 0;
for (int j = 0; j < n; ++j) {
// Skip the current column
if (j == col) continue;
// Fill the submatrix
sub[i - 1LL][subcol++] = mat[i][j];
}
}
// Cofactor expansion
int sign = (col % 2 == 0) ? 1 : -1;
std::complex<double> csign(sign, 0.0);
res = res + csign * mat[0][col] * getDet(sub, n - 1);
}
return res;
}
std::complex<double> CmpLinearAlgebra::CmpDeterminant(
int n, std::vector<std::vector<std::complex<double>>>& A)
{
return getDet(A, A.size());
}
bool CmpLinearAlgebra::CmpGaussianElimination(
int m, int n,
std::vector<std::vector<std::complex<double>>>& A,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot)
{
bool failure = false;
std::vector<std::complex<double>> c(m);
b.resize(n);
x.resize(n);
for (size_t i = 0; i < m; i++)
c[i] = -1;
for (size_t j = 0; j < n; j++)
{
bool found = false;
size_t i = j;
while (i < n && !found)
{
if (abs(A[i][j]) != 0)
found = true;
else
i++;
}
if (!found)
{
failure = true;
break;
}
if (i > j)
{
for (size_t l = j; l < n; l++)
{
std::complex<double> t = A[i][l];
A[i][l] = A[j][l];
A[j][l] = t;
t = b[i];
b[i] = b[j];
b[j] = t;
}
}
std::complex<double> d = 1.0 / A[j][j];
for (size_t k = j + 1; k < n; k++)
c[k] = d * A[k][j];
for (size_t k = j + 1; k < n; k++)
{
for (size_t l = j + 1; l < n; l++)
A[k][l] = A[k][l] - c[k] * A[j][l];
b[k] = b[k] - c[k] * b[j];
}
}
for (long long i = (long long)n - 1; i >= 0; i--)
{
std::complex<double> sum = 0;
for (size_t j = i + 1; j < n; j++)
sum += A[i][j] * x[j];
x[i] = (b[i] - sum) / A[i][i];
}
return failure;
}
bool CmpLinearAlgebra::CmpSubstitution(
int m, int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot)
{
std::complex<double> sum = 0;
size_t n1 = n - 1LL;
if (n == 1)
{
x[0] = b[0] / M[0][0];
return true;
}
// forward substitution
x[0] = b[pivot[0]];
for (size_t i = 1; i < n; i++)
{
std::complex<double> sum = 0;
for (size_t j = 0; j < i; j++)
sum += M[i][j] * x[j];
x[i] = b[pivot[i]] - sum;
}
// backward substitution
x[n1] /= M[n1][n1];
for (long long i = n - 2LL; i >= 0; i--)
{
std::complex<double> sum = 0;
for (size_t j = i + 1; j < n; j++)
sum += M[i][j] * x[j];
x[i] = (x[i] - sum) / M[i][i];
}
return true;
}
static std::complex<double> complex_max(
std::complex<double> a, std::complex<double> b) {
return (std::abs(a) > std::abs(b)) ? a : b;
}
bool CmpLinearAlgebra::CmpGaussianFactor(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<size_t>& pivot)
{
// returns false if matrix is singular
std::vector<std::complex<double>> d(n);
std::complex<double> awikod = 0, col_max = 0, ratio = 0, row_max = 0, temp = 0;
int flag = 1;
size_t i_star, itemp;
for (size_t i = 0; i < n; i++)
{
pivot[i] = i;
row_max = 0;
for (size_t j = 0; j < n; j++)
row_max = complex_max(row_max, abs(M[i][j]));
if (abs(row_max) == 0)
{
flag = 0;
row_max = 1;
}
d[i] = row_max;
}
if (n <= 1) return flag != 0;
// factorization
for (size_t k = 0; k < (size_t)n - 1LL; k++)
{
// determine pivot row the row i_star
col_max = abs(M[k][k]) / d[k];
i_star = k;
for (size_t i = k + 1; i < n; i++)
{
awikod = abs(M[i][k]) / d[i];
if (abs(awikod) > abs(col_max))
{
col_max = awikod;
i_star = i;
}
}
if (abs(col_max) == 0)
flag = 0;
else
{
if (i_star > k)
{
// make k the pivot row by
// interchanging with i_star
flag *= -1;
itemp = pivot[i_star];
pivot[i_star] = pivot[k];
pivot[k] = itemp;
temp = d[i_star];
d[i_star] = d[k];
d[k] = temp;
for (size_t j = 0; j < n; j++)
{
temp = M[i_star][j];
M[i_star][j] = M[k][j];
M[k][j] = temp;
}
}
// eliminate x[k]
for (size_t i = k + 1; i < n; i++)
{
M[i][k] /= M[k][k];
ratio = M[i][k];
for (size_t j = k + 1; j < n; j++)
M[i][j] -= ratio * M[k][j];
}
}
if (abs(M[n - 1LL][n - 1LL]) == 0) flag = 0;
}
if (flag == 0)
return false;
return true;
}
bool CmpLinearAlgebra::CmpGaussianSolution(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::complex<double>>& b,
std::vector<std::complex<double>>& x,
std::vector<size_t>& pivot)
{
if (!CmpGaussianFactor(n, M, pivot))
return false;
return CmpSubstitution(n, n, M, b, x, pivot);
}
bool CmpLinearAlgebra::CmpInverse(
int n, std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& Mi)
{
std::vector<std::complex<double>> b(n);
std::vector<std::complex<double>> x(n);
std::vector<size_t> pivot(n);
std::vector<std::vector<std::complex<double>>> Mc(n,
std::vector<std::complex<double>>(n));
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
Mc[i][j] = M[i][j];
}
}
if (!CmpGaussianFactor(n, Mc, pivot))
return false;
for (size_t i = 0; i < n; i++)
{
b[i] = 0;
}
for (size_t i = 0; i < n; i++)
{
b[i] = 1;
if (!CmpSubstitution(n, n, Mc, b, x, pivot))
return false;
b[i] = 0;
for (size_t j = 0; j < n; j++)
Mi[j][i] = x[j];
}
return true;
}
void CmpLinearAlgebra::CmpCharPolyAndAdjoint(
int n,
std::vector<std::vector<std::complex<double>>>& C,
std::vector<std::vector<std::complex<double>>>& I,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& adjoint,
std::vector<std::complex<double>>& a)
{
C.resize(n, std::vector<std::complex<double>>(n));
I.resize(n, std::vector<std::complex<double>>(n));
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
C[i][j] = I[i][j] = 0;
}
for (size_t i = 0; i < n; i++)
C[i][i] = I[i][i] = 1;
a[0] = 1;
for (size_t i = 1; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
for (size_t k = 0; k < n; k++)
{
std::complex<double> sum = 0.0;
for (size_t l = 0; l < n; l++)
sum += M[j][l] * C[l][k];
C[j][k] = sum;
}
}
std::complex<double> tr = 0.0;
for (size_t j = 0; j < n; j++)
tr += C[j][j];
std::complex<double> ci = 0;
ci._Val[0] = (double)i;
a[i] = -tr / ci;
for (size_t j = 0; j < n; j++)
{
for (size_t k = 0; k < n; k++)
C[j][k] += a[i] * I[j][k];
}
}
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
std::complex<double> sum = 0.0;
for (size_t k = 0; k < n; k++)
sum += M[i][k] * C[k][j];
C[i][j] = sum;
}
}
std::complex<double> trace = 0.0;
for (size_t i = 0; i < n; i++)
trace += C[i][i];
trace /= n;
a[n - 1LL] = -trace;
std::complex<double> factor = 1.0;
if ((n - 1) % 2 != 0)
factor = -1.0;
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
adjoint[i][j] = factor * C[i][j];
}
}
void CmpLinearAlgebra::CmpMatrixKernel(
int m, int n,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& X,
size_t& r)
{
std::complex<double> D = 0;
std::vector<int> c(m);
std::vector<int> d(n);
r = 0;
for (size_t i = 0; i < m; i++)
c[i] = -1;
size_t j = 0, k = 1;
Step2:
for (j = 0; j < m; j++)
{
if (abs(M[j][k]) != 0 && c[j] == -1)
break;
}
if (j == m)
{
r++;
d[k] = 0;
goto Step4;
}
D = -1.0 / M[j][k];
M[j][k] = -1;
for (size_t s = k + 1; s < n; s++)
{
M[j][s] = D * M[j][s];
for (size_t i = 0; i < m; i++)
{
if (i != j)
{
D = M[i][k];
M[i][k] = 0;
}
}
}
for (size_t s = k + 1; s < n; s++)
{
for (size_t i = 0; i < m; i++)
{
M[i][s] += D * M[j][s];
}
}
c[j] = (int)k;
d[k] = (int)j;
Step4:
if (k < n - 1)
{
k++;
goto Step2;
}
X.resize(n, std::vector<std::complex<double>>(n));
if (r != 0)
{
for (k = 0; k < n; k++)
{
if (d[k] == 0)
{
for (size_t i = 0; i < n; i++)
{
if (d[i] > 0)
X[k][i] = M[d[i]][k];
else if (i == k)
X[k][i] = 1;
else
X[k][i] = 0;
}
}
}
}
}
void CmpLinearAlgebra::CmpMatrixImage(
int m, int n,
std::vector<std::vector<std::complex<double>>>& M,
std::vector<std::vector<std::complex<double>>>& N,
std::vector<std::vector<std::complex<double>>>& X,
int rank)
{
std::complex<double> D = 0.0;
size_t r = 0;
std::vector<std::vector<std::complex<double>>> copyM(
m, std::vector<std::complex<double>>(n));
std::vector<int> c(m);
std::vector<int> d(n);
for (size_t i = 0; i < m; i++)
c[i] = -1;
size_t j = 0, k = 1;
for (size_t i = 0; i < m; i++)
{
for (size_t j = 0; j < n; j++)
{
N[i][j] = copyM[i][j] = M[i][j];
}
}
Step2:
for (size_t j = 0; j < m; j++)
{
if (abs(copyM[j][k]) != 0 && c[j] == -1)
break;
}
if (j == m)
{
r++;
d[k] = 0;
goto Step4;
}
D = -1.0 / copyM[j][k];
copyM[j][k] = -1;
for (size_t s = k + 1; s < n; s++)
{
copyM[j][s] = D * copyM[j][s];
for (size_t i = 0; i < m; i++)
{
if (i != j)
{
D = copyM[i][k];
copyM[i][k] = 0;
}
}
}
for (size_t s = k + 1; s < n; s++)
{
for (size_t i = 0; i < m; i++)
{
copyM[i][s] += D * copyM[j][s];
}
}
c[j] = (int)k;
d[k] = (int)j;
Step4:
if (k < (size_t)(n - 1LL))
{
k++;
goto Step2;
}
rank = (int)(n - r);
for (j = 0; j < m; j++)
{
if (c[j] != 0)
{
for (size_t i = 0; i < m; i++)
{
N[i][c[j]] = M[i][c[j]];
}
}
}
}
void CmpLinearAlgebra::CmpGenerateNonSingular(
double scale, std::complex<double>& cDeterminant,
int n, unsigned int seed,
std::vector<std::vector<std::complex<double>>>& Mc)
{
bool failure = false;
std::mt19937 rng(seed);
std::uniform_real_distribution<double> dist(0.0, 1.0);
while (true)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
Mc[i][j]._Val[0] = scale * dist(rng);
Mc[i][j]._Val[1] = scale * dist(rng);
}
}
cDeterminant = CmpDeterminant(n, Mc);
if (cDeterminant._Val[0] != 0 || cDeterminant._Val[1] != 0)
break;
}
}
// Exercises from "Modern Quantum Chemistry an Introduction to Advanced
// Electronic Structure Theory" by Attila Szabo and Neil S. Ostlund
// https://chemistlibrary.wordpress.com/wp-content/uploads/2015/02/modern-quantum-chemistry.pdf
// Program (c) Tuesday, August 12, 2025 by James Pate Williams, Jr.
// Program (c) Tuesday, August 19, 2025 by James Pate Williams, Jr.
#include <complex>
#include <iomanip>
#include <iostream>
#include <vector>
#include "DblLinearAlgebra.h"
#include "CmpLinearAlgebra.h"
int main()
{
// static data matrices
double AArcb[3][3] = { { 2, 3, -1 }, { 4, 4, -3 }, { -2, 3, -1 } };
double AArso[3][3] = { { 1, 1, 0 }, { 1, 2, 2 }, { 0, 2, -1 } };
double BBrso[3][3] = { { 1, -1, 1 }, { -1, 0, 0 }, { 1, 0, 1} };
double BBr[3][3] = { { 1, -1, 1 }, { -1 , 0, 0 }, { 1, 0, 1 } };
double AAcr[3][3] = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
double AAci[3][3] = { { 1, 1, 2 }, { 3, 0, 1 }, { 0, 2, 4 } };
double BBcr[3][3] = { { 1, 0, 1 }, { 1 , 1, 0 }, { 0, 1, 1 } };
double BBci[3][3] = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
// some array dimensions
int m = 3, n = 3, p = 3;
// a couple of 3x1 vectors
std::vector<double> br(3);
std::vector<size_t> pivot(3);
// 3x3 real matrices
std::vector<std::vector<double>> Arcb(3, std::vector<double>(3));
std::vector<std::vector<double>> Arso(3, std::vector<double>(3));
std::vector<std::vector<double>> Brso(3, std::vector<double>(3));
std::vector<std::vector<double>> Br(3, std::vector<double>(3));
std::vector<std::vector<double>> Cr(3, std::vector<double>(3));
std::vector<std::vector<double>> Ai(3, std::vector<double>(3));
std::vector<std::vector<double>> Ari(3, std::vector<double>(3));
// a 4x4 real matrix
std::vector<std::vector<double>> Mr(4, std::vector<double>(4));
// 3x3 complex matrices
std::vector<std::vector<std::complex<double>>> Ac(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Bc(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Cc(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Dc(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Ec(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Fc(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Gc(3,
std::vector<std::complex<double>>(3));
std::vector<std::vector<std::complex<double>>> Mc(4,
std::vector<std::complex<double>>(4));
// copy static real matrices to dynamic matrices
for (int i = 0; i < m; i++)
{
for (int j = 0; j < p; j++)
{
Arcb[i][j] = AArcb[i][j];
Arso[i][j] = AArso[i][j];
Brso[i][j] = BBrso[i][j];
Ac[i][j]._Val[0] = AAcr[i][j];
Ac[i][j]._Val[1] = AAci[i][j];
}
}
// copy static complex matrices to dynamic matrices
for (int i = 0; i < p; i++)
{
for (int j = 0; j < n; j++)
{
Br[i][j] = BBr[i][j];
Bc[i][j]._Val[0] = BBcr[i][j];
Bc[i][j]._Val[1] = BBci[i][j];
}
}
// See "Elementary Numerical Analysis an
// Algorithmic Approach" (c) 1980 by S. D. Conte
// and Carl de Boor
DblLinearAlgebra::DblMultiply(3, 3, 3, Arcb, Br, Cr);
std::cout << "Ar * Br = Cr Conte & de Boor" << std::endl;
DblLinearAlgebra::DblPrintMatrix(3, 3, Cr);
std::cout << std::endl;
// complex matrix multiplication
CmpLinearAlgebra::CmpMultiply(3, 3, 3, Ac, Bc, Cc);
std::cout << "Ac * Bc = Cc" << std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Cc);
std::cout << std::endl;
// Exercise 1.2 from Szabo and Ostlund
std::cout << "Exercise 1.2 page 5 Commutator" << std::endl;
DblLinearAlgebra::DblCommutator(3, Arso, Brso, Cr);
DblLinearAlgebra::DblPrintMatrix(3, 3, Cr);
std::cout << std::endl;
std::cout << "Exercise 1.2 page 5 Anticommutator" << std::endl;
DblLinearAlgebra::DblAnticommutator(3, Arso, Brso, Cr);
DblLinearAlgebra::DblPrintMatrix(3, 3, Cr);
std::cout << std::endl;
CmpLinearAlgebra::CmpAdjoint(3, 3, Cc, Dc);
std::cout << "Exercise 1.3 page 6 Cc adjoint" << std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Dc);
std::cout << std::endl;
CmpLinearAlgebra::CmpAdjoint(3, 3, Ac, Ec);
CmpLinearAlgebra::CmpAdjoint(3, 3, Bc, Fc);
CmpLinearAlgebra::CmpMultiply(3, 3, 3, Fc, Ec, Gc);
std::cout << "Exercise 1.3 page 6 Bc adjoint * Ac adjoint"
<< std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Gc);
std::cout << std::endl;
std::cout << "Ar matrix" << std::endl;
DblLinearAlgebra::DblPrintMatrix(3, 3, Arcb);
bool inv = DblLinearAlgebra::DblInverse(n, Arcb, Ai);
std::cout << std::endl;
std::cout << "Ar Conte & de Boor inverse flag = "
<< inv << std::endl;
DblLinearAlgebra::DblPrintMatrix(3, 3, Ai);
std::cout << std::endl;
std::cout << "Ar * Ar inverse" << std::endl;
DblLinearAlgebra::DblMultiply(3, 3, 3, Arcb, Ai, Ari);
DblLinearAlgebra::DblPrintMatrix(3, 3, Ari);
std::cout << std::endl;
double rDeterminant = 0;
DblLinearAlgebra::DblGenerateNonSingular(
2.0, rDeterminant, 4, 1, Mr);
std::cout << "rDeterminant = ";
std::cout << rDeterminant << std::endl;
std::cout << std::endl;
std::cout << "Ac" << std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Ac);
std::cout << std::endl;
inv = CmpLinearAlgebra::CmpInverse(3, Ac, Bc);
std::cout << "Ac inverse flag = " << inv << std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Bc);
CmpLinearAlgebra::CmpMultiply(3, 3, 3, Ac, Bc, Cc);
std::cout << std::endl;
std::cout << "Ac * Ac inverse" << std::endl;
CmpLinearAlgebra::CmpPrintMatrix(3, 3, Cc);
std::complex<double> cDeterminant = 0;
CmpLinearAlgebra::CmpGenerateNonSingular(
2.0, cDeterminant, 4, 1, Mc);
std::cout << std::endl;
std::cout << "complex determinant = ";
std::cout << cDeterminant << std::endl;
double rDeterminantA = 0;
std::vector<std::vector<double>> A44r(4,
std::vector<double>(4));
DblLinearAlgebra::DblGenerateNonSingular(
2.0, rDeterminantA, 4, 2, A44r);
double rDeterminantB = 0;
std::vector<std::vector<double>> B44r(4,
std::vector<double>(4));
DblLinearAlgebra::DblGenerateNonSingular(
2.0, rDeterminantB, 4, 3, B44r);
std::cout << std::endl;
std::vector<std::vector<double>> C44r(4,
std::vector<double>(4));
DblLinearAlgebra::DblMultiply(4, 4, 4, A44r, B44r, C44r);
std::cout << "|A| = " << rDeterminantA << std::endl;
std::cout << "|B| = " << rDeterminantB << std::endl;
bool failure = false;
double rDeterminantC =
DblLinearAlgebra::DblDeterminant(4, 0, 0, C44r);
std::cout << "|AB| = " << rDeterminantC << std::endl;
std::cout << "|A||B| = " << rDeterminantA *
rDeterminantB << std::endl;
// Exercise 1.6 with 4x4 complex determinants
std::vector<std::vector<std::complex<double>>> A44c(4,
std::vector<std::complex<double>>(4));
std::cout << std::endl;
std::complex<double> cDeterminantA = 0;
CmpLinearAlgebra::CmpGenerateNonSingular(
2.0, cDeterminantA, 4, 2, A44c);
std::vector<std::vector<std::complex<double>>> B44c(4,
std::vector<std::complex<double>>(4));
std::complex<double> cDeterminantB = 0;
CmpLinearAlgebra::CmpGenerateNonSingular(
2.0, cDeterminantB, 4, 3, B44c);
std::vector<std::vector<std::complex<double>>> C44c(4,
std::vector<std::complex<double>>(4));
CmpLinearAlgebra::CmpMultiply(4, 4, 4, A44c, B44c, C44c);
std::cout << "|A| = " << cDeterminantA << std::endl;
std::cout << "|B| = " << cDeterminantB << std::endl;
failure = false;
std::complex<double> cDeterminantC =
CmpLinearAlgebra::CmpDeterminant(4, C44c);
std::cout << "|AB| = " << cDeterminantC << std::endl;
std::cout << "|A||B| = " << cDeterminantA *
cDeterminantB << std::endl;
std::cout << "\nEnter any key to halt: ";
char line[128] = "";
std::cin.getline(line, 128);
}
Blog Entry © Thursday, January 23, 2025, by James Pate Williams, Jr. Three Classical Iterative and Two Direct Linear Equation Solvers
Blog Entry © Tuesday, January 7 – Thursday, January 9, 2025, by James Pate Williams, Jr. Solution of a System of Nonlinear Equations Using Damped Newton’s Method for a System of Equations
Live Person-to-Person Tutoring
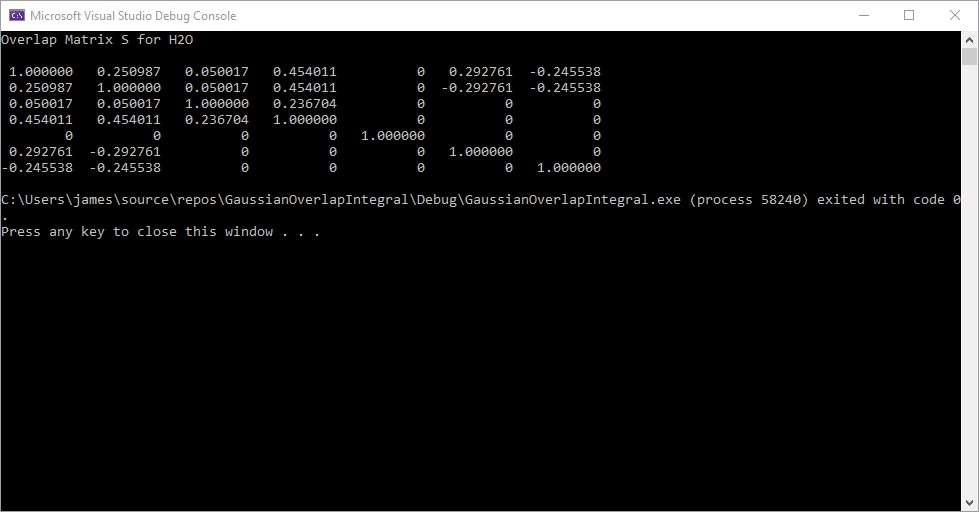
Blog Entry © Friday, November 1, 2024, by James Pate Williams, Jr. Calculation of the Overlap Matrix for the Water Molecule (H2O) Using a Contracted Set of Gaussian Orbitals
Reference: https://content.wolfram.com/sites/19/2012/02/Ho.pdf
I reproduced most of the computations in the MATHMATICA reference. The water molecule is a planar molecule that lies in the YZ-plane.