Category: Cubic Formula
Blog Entry (c) Tuesday, July 23, 2024, by James Pate Williams, Jr. Mueller’s Method for Finding the Complex and/or Real Roots of a Complex and/or Real Polynomial
I originally implemented this algorithm in FORTRAN IV in the Summer Quarter of 1982 at the Georgia Institute of Technology. I was taking a course named “Scientific Computing I” taught by Professor Gunter Meyer. I made a B in the class. Later in 2015 I re-implemented the recipe in C# using Visual Studio 2008 Professional. VS 2015 did not have support for complex numbers nor large integers. In December of 2015 I upgraded to Visual Studio 2015 Professional which has support for big integers and complex numbers. I used Visual Studio 2019 Community version for this project. Root below should be function.
Degree (0 to quit) = 2
coefficient[2].real = 1
coefficient[2].imag = 0
coefficient[1].real = 1
coefficient[1].imag = 0
coefficient[0].real = 1
coefficient[0].imag = 0
zero[0].real = -5.0000000000e-01 zero[0].imag = 8.6602540378e-01
zero[1].real = -5.0000000000e-01 zero[1].imag = -8.6602540378e-01
root[0].real = 0.0000000000e+00 root[0].imag = -2.2204460493e-16
root[1].real = 3.3306690739e-16 root[1].imag = -7.7715611724e-16
Degree (0 to quit) = 3
coefficient[3].real = 1
coefficient[3].imag = 0
coefficient[2].real = 0
coefficient[2].imag = 0
coefficient[1].real = -18.1
coefficient[1].imag = 0
coefficient[0].real = -34.8
coefficient[0].imag = 0
zero[0].real = -2.5026325486e+00 zero[0].imag = -8.3036679880e-01
zero[1].real = -2.5026325486e+00 zero[1].imag = 8.3036679880e-01
zero[2].real = 5.0052650973e+00 zero[2].imag = 2.7417672687e-15
root[0].real = 0.0000000000e+00 root[0].imag = 1.7763568394e-15
root[1].real = 3.5527136788e-14 root[1].imag = -1.7763568394e-14
root[2].real = 2.8421709430e-14 root[2].imag = 1.5643985575e-13
Degree (0 to quit) = 5
coefficient[5].real = 1
coefficient[5].imag = 0
coefficient[4].real = 2
coefficient[4].imag = 0
coefficient[3].real = 3
coefficient[3].imag = 0
coefficient[2].real = 4
coefficient[2].imag = 0
coefficient[1].real = 5
coefficient[1].imag = 0
coefficient[0].real = 6
coefficient[0].imag = 0
zero[0].real = -8.0578646939e-01 zero[0].imag = 1.2229047134e+00
zero[1].real = -8.0578646939e-01 zero[1].imag = -1.2229047134e+00
zero[2].real = 5.5168546346e-01 zero[2].imag = 1.2533488603e+00
zero[3].real = 5.5168546346e-01 zero[3].imag = -1.2533488603e+00
zero[4].real = -1.4917979881e+00 zero[4].imag = 1.8329656063e-15
root[0].real = 8.8817841970e-16 root[0].imag = 4.4408920985e-16
root[1].real = -2.6645352591e-15 root[1].imag = -4.4408920985e-16
root[2].real = 8.8817841970e-16 root[2].imag = 1.7763568394e-15
root[3].real = 3.4638958368e-14 root[3].imag = -1.4210854715e-14
root[4].real = 8.8817841970e-16 root[4].imag = 2.0710031449e-14
Python Root Finder for Linear, Quadratic, Cubic, and Quartic Equations by James Pate Williams, Jr.
z1 = complex(0, 0)
z2 = complex(0, 0)
z3 = complex(0, 0)
z4 = complex(0, 0)
def complex_quadratic_formula(a, b, c):
import cmath
z1 = complex((-b + cmath.sqrt(b * b - 4 * a * c)) / (2 * a))
z2 = complex((-b - cmath.sqrt(b * b - 4 * a * c)) / (2 * a))
print("z1 = ", z1)
print("z2 = ", z2)
def real_quadratic_formula(a, b, c):
if b * b - 4 * a * c >= 0:
import math
z1 = float((-b + math.sqrt(b * b - 4 * a * c)) / (2 * a))
z2 = float((-b - math.sqrt(b * b - 4 * a * c)) / (2 * a))
else:
import cmath
z1 = complex((-b + cmath.sqrt(b * b - 4 * a * c)) / (2 * a))
z2 = complex((-b - cmath.sqrt(b * b - 4 * a * c)) / (2 * a))
print("z1 = ", z1)
print("z2 = ", z2)
def cubic_equation(A, B, C, D):
# https://en.wikipedia.org/wiki/Cubic_function
# http://www.wolframalpha.com/widgets/view.jsp?id=3f4366aeb9c157cf9a30c90693eafc55
import cmath
import math
A2 = float(A * A)
B2 = float(B * B)
B3 = float(B * B * B)
C2 = float(C * C)
C3 = float(C * C * C)
D2 = float(D * D)
Delta = float(18 * A * B * C * D - 4.0 * B3 * D
+ B2 * C2 - 4.0 * A * C3 - 27.0 * A2 * D2)
Delta0 = float(B2 - 3.0 * A * C)
Delta1 = float(2.0 * B3 - 9.0 * A * B * C + 27.0 * A2 * D)
r = cmath.sqrt(-27.0 * A2 * Delta)
c = complex(0.5 * (Delta1 + r)) ** (1.0 / 3.0)
d = complex(0.5 * (Delta1 - r)) ** (1.0 / 3.0)
if c.real == 0 and c.imag == 0:
c = d
i = complex(0.0, 1.0)
chi = complex(-0.5, 0) + i * 0.5 * math.sqrt(3)
import array
ar = array.array('f', [0,0,0])
ai = array.array('f', [0,0,0])
for k in range(0, 3, 1):
chik = chi ** k
z = -(B + chik * c + Delta0 / (chik * c)) / (3.0 * A)
ar[k] = z.real
ai[k] = z.imag;
z1 = ar[0] + ai[0] * complex(0, 1);
z2 = ar[1] + ai[1] * complex(0, 1);
z3 = ar[2] + ai[2] * complex(0, 1);
print("z1 = ", z1)
print("z2 = ", z2)
print("z3 = ", z3)
def quartic_equation(A, B, C, D, E):
# https://en.wikipedia.org/wiki/Quartic_function
# https://keisan.casio.com/exec/system/1181809416
import cmath
A2 = float(A * A)
A3 = float(A * A2)
A4 = float(A2 * A2)
B2 = float(B * B)
B3 = float(B * B2)
B4 = float(B2 * B2)
C2 = float(C * C)
C3 = float(C * C2)
C4 = float(C2 * C2)
D2 = float(D * D)
D3 = float(D * D2)
D4 = float(D2 * D2)
E2 = float(E * E)
E3 = float(E * E2)
E4 = float(E2 * E2)
Delta = float(256 * A3 * E3 - 192 * A2 * B * D * E2
- 128 * A2 * C2 * E2 + 144 * A2 * C * D2 * E
- 27 * A2 * D4 + 144 * A * B2 * C * E2
- 6 * A * B2 * D2 * E - 80 * A * B * C2 * D * E
+ 18 * A * B * C * D3 + 16 * A * C4 * E
- 4 * A * C3 * D2 - 27 * B4 * E2 + 18 * B3 * C * D * E
- 4 * B3 * D3 - 4 * B2 * C3 * E + B2 * C2 * D2)
Delta0 = float(C2 - 3 * B * D + 12 * A * E)
Delta1 = float(2 * C3 - 9 * B * C * D
+ 27 * B2 * E + 27 * A * D2 - 72 * A * C * E)
p = float((8 * A * C - 3 * B2) / (8 * A2))
q = float((B3 - 4 * A * B * C + 8 * A2 * D) / (8 * A3))
R = cmath.sqrt(Delta1 * Delta1 - 4 * Delta0 * Delta0 * Delta0)
P = cmath.sqrt(-27 * Delta)
Q = complex(0.5 * (Delta1 + P)) ** complex(1.0 / 3.0)
S = 0.5 * cmath.sqrt(((-2.0 * p) / 3.0)
+ (Q + Delta0 / Q) / (3 * A))
a = complex(-B / (4 * A), 0)
s = 0.5 * cmath.sqrt(-4 * S * S - 2 * p + q / S)
z1 = a - S + s
z2 = a - S - s
s = 0.5 * cmath.sqrt(-4 * S * S - 2 * p - q / S)
z3 = a + S + s
z4 = a + S - s
print("z1 = ", z1)
print("z2 = ", z2)
print("z3 = ", z3)
print("z4 = ", z4)
option = int(1)
print("Menu")
print("1 Solve a linear equation")
print("2 Solve a quadratic eqution")
print("3 Solve a cubic equation")
print("4 Solve a quartic equation")
print("5 Quit")
option = int(input("Option 1 to 5: "))
while option != 5:
if option >= 1:
a = float(input("a = "))
b = float(input("b = "))
if option >= 2:
c = float(input("c = "))
if option >= 3:
d = float(input("d = "))
if option == 4:
e = float(input("e = "))
if option == 1:
z1 = -b / a
print("z1 = ", z1)
elif option == 2:
real_quadratic_formula(a, b, c)
elif option == 3:
cubic_equation(a, b, c, d)
elif option == 4:
quartic_equation(a, b, c, d, e)
option = int(input("Option 1 to 5: "))

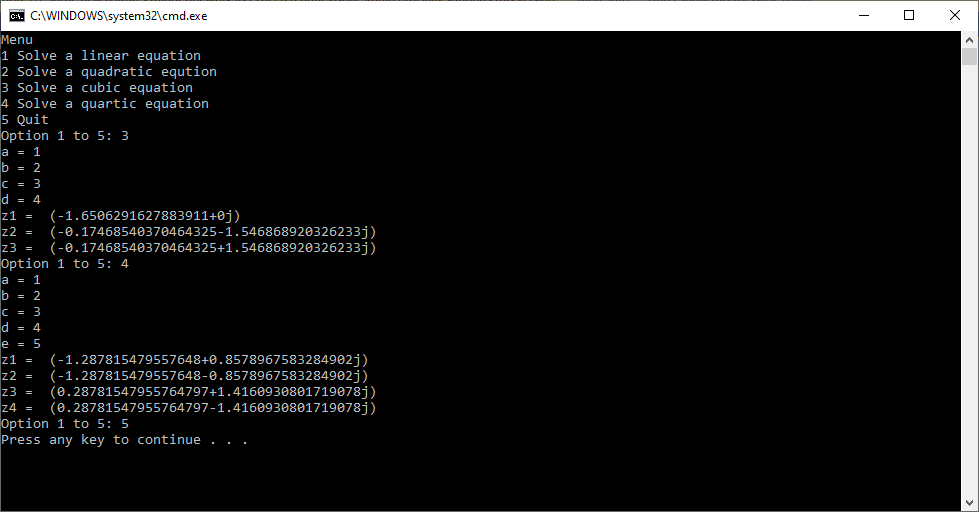
Quadratic, Cubic, and Quartic Python Equation Solver by James Pate Williams Jr
Back in 2015 I created a C# application to solve quadratic, cubic, and quartic equations which are of degrees 2, 3, and 4, respectively. Yesterday I successfully translated the C# to the Python console. I bench-marked my computer programs against the online calculators on the following website:
Cubic equation Calculator – High accuracy calculation (casio.com)
Quartic equation Calculator – High accuracy calculation (casio.com)
Here are my resulting Python outputs:


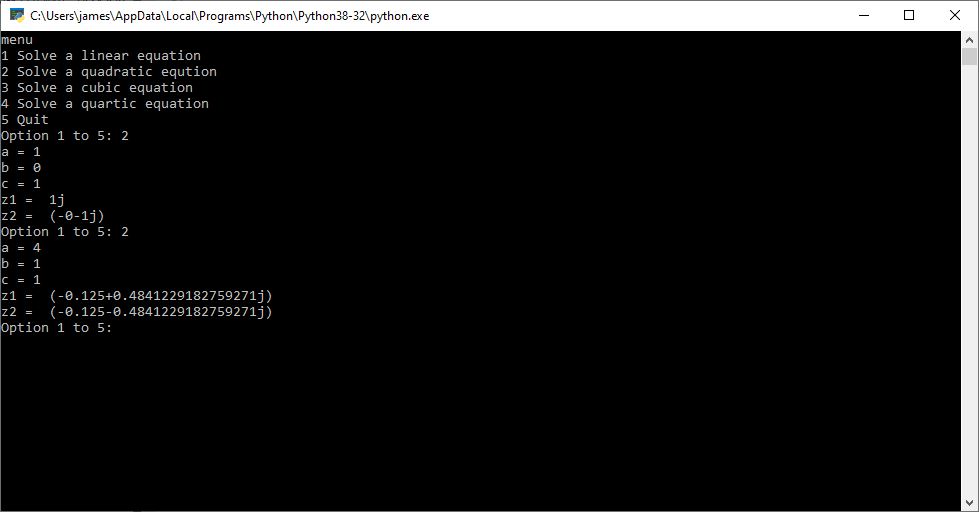

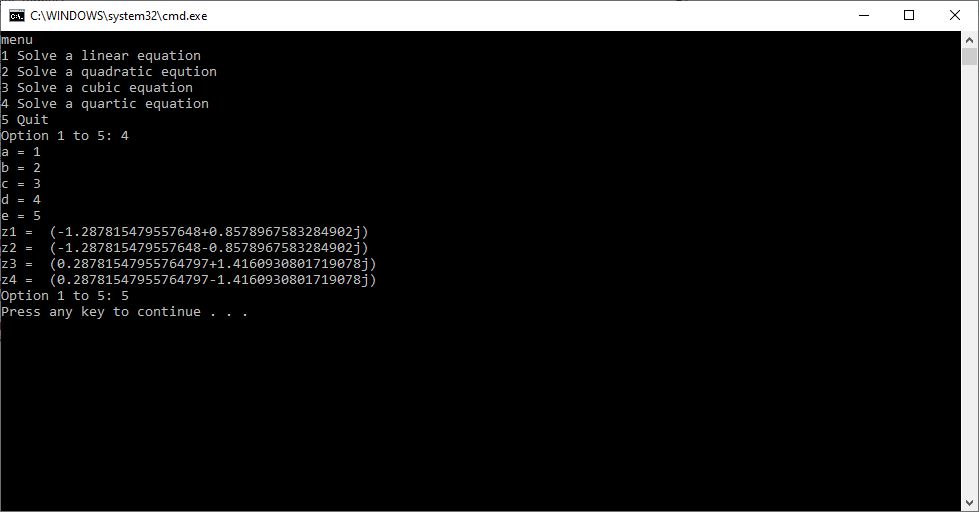
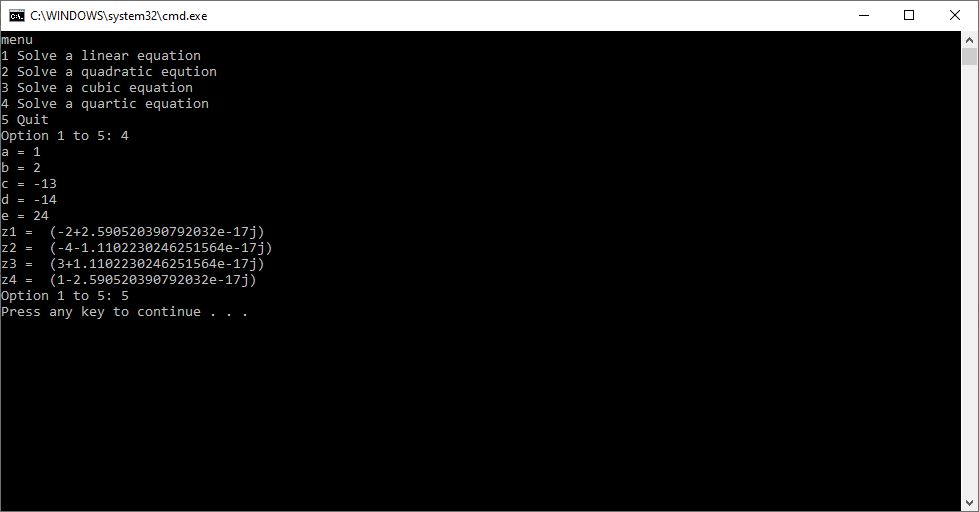
Roots of Small Degree Polynomials with Real Coefficients by James Pate Williams, BA, BS, MSwE, PhD
We designed and implemented quadratic formula, cubic formula, and quartic formula solvers using the formulas in the Wikipedia articles:
https://en.wikipedia.org/wiki/Quadratic_formula
https://en.wikipedia.org/wiki/Cubic_function
https://en.wikipedia.org/wiki/Quartic_function
We tested our C# implementation against:
https://keisan.casio.com/exec/system/1181809415
http://www.wolframalpha.com/widgets/view.jsp?id=3f4366aeb9c157cf9a30c90693eafc55
https://keisan.casio.com/exec/system/1181809416
Here are screenshots of the C# application:
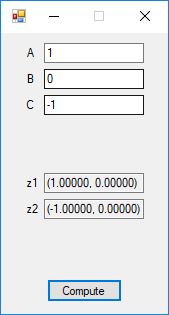
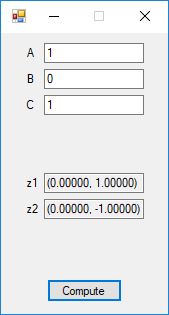
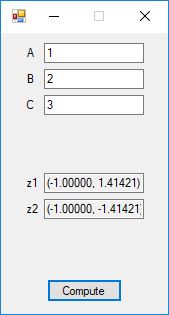
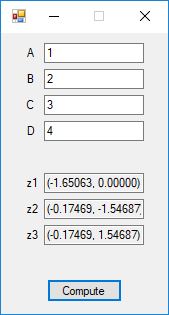
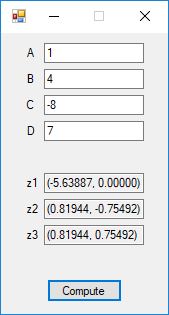
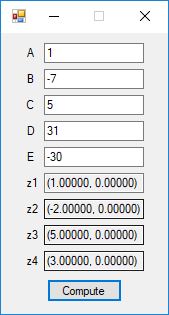
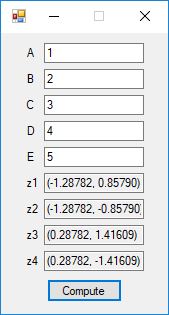
C# source code files for the application: