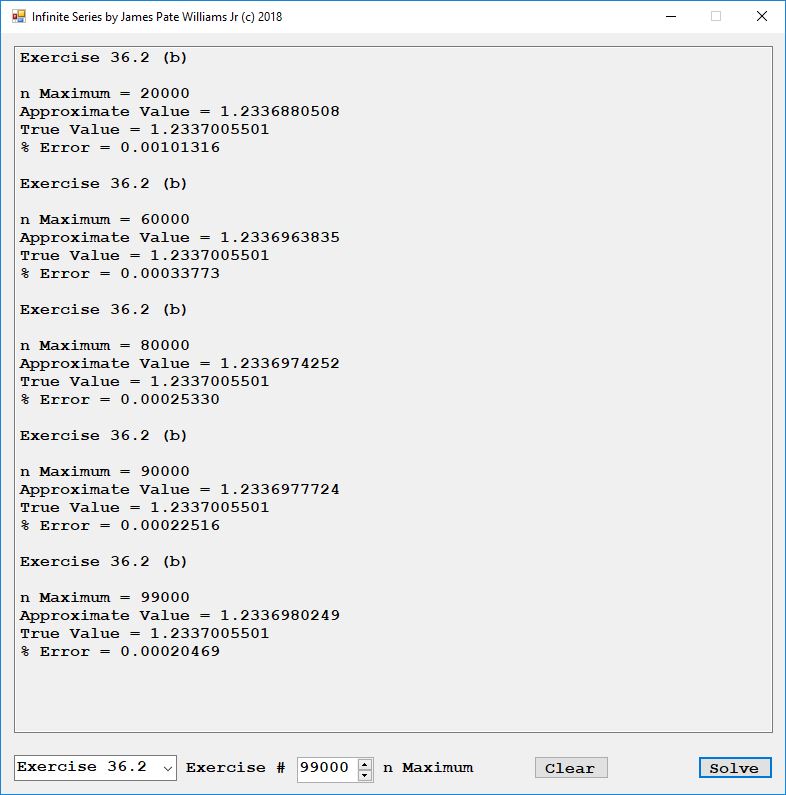
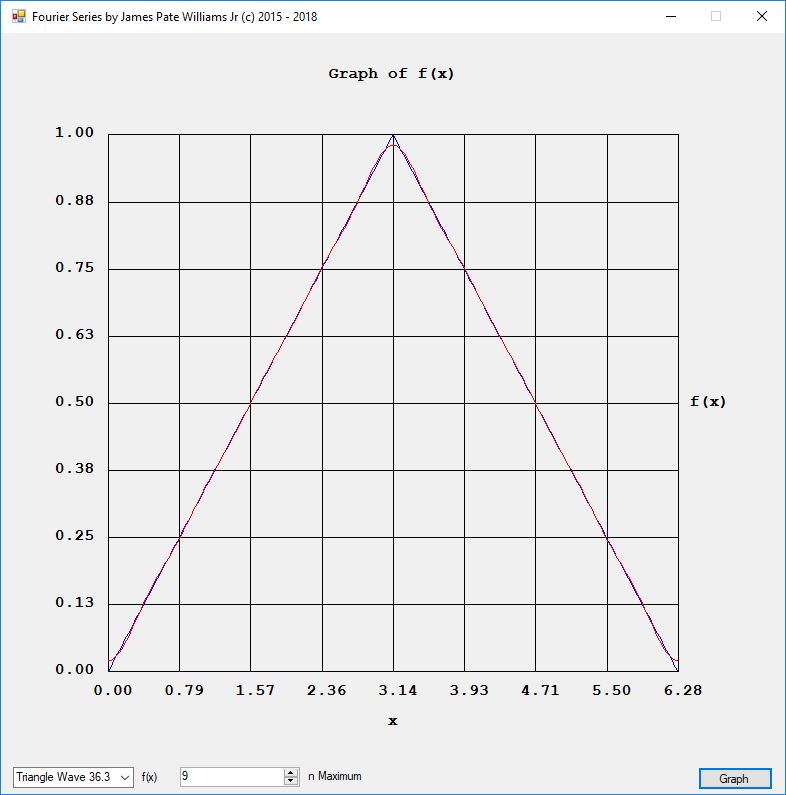
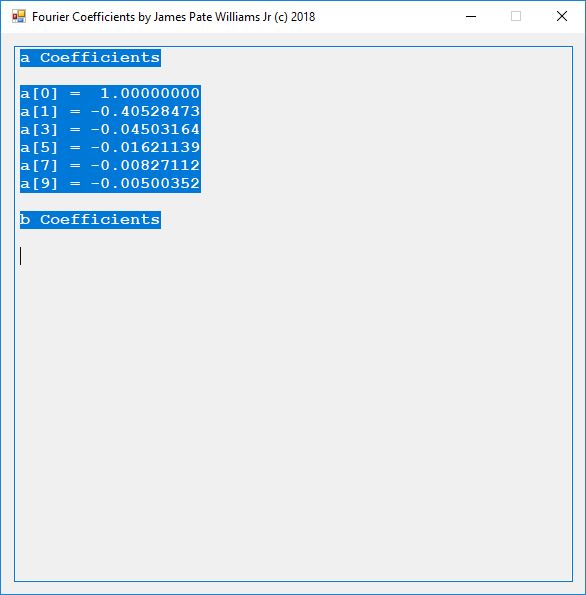
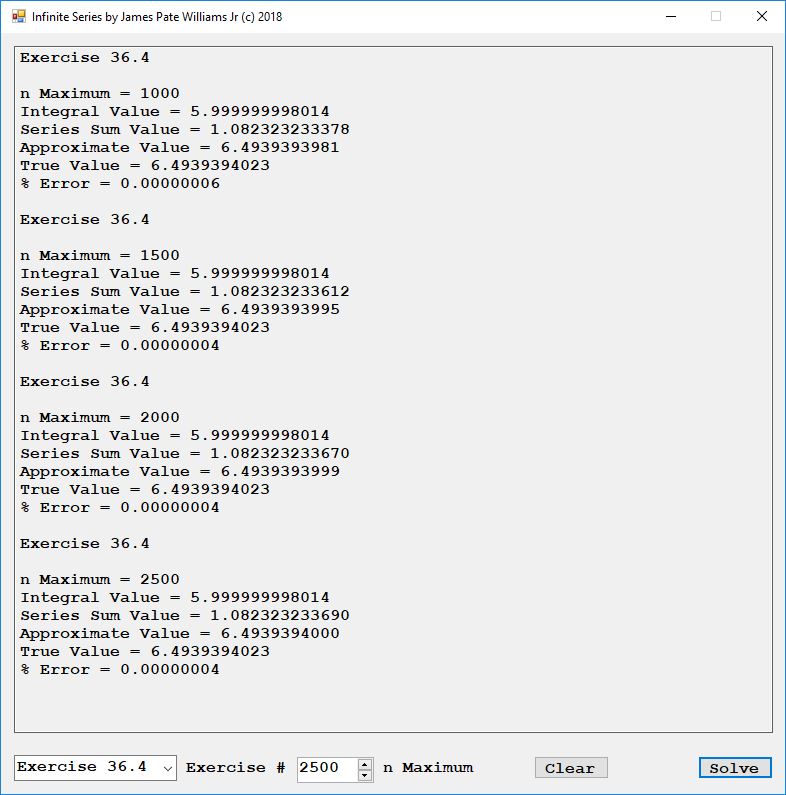
Solve the Laplace equation in the following orthogonal rectilinear coordinate systems:
- Cartesian coordinates
- Cylindrical coordinates
- Spherical polar coordinates
- Parabolic cylindrical coordinates
Solution PDF:
Solve the Laplace equation in the following orthogonal rectilinear coordinate systems:
Solution PDF:
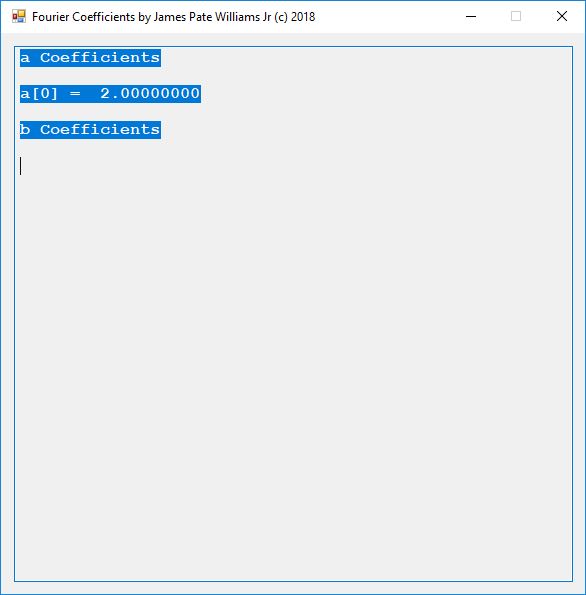
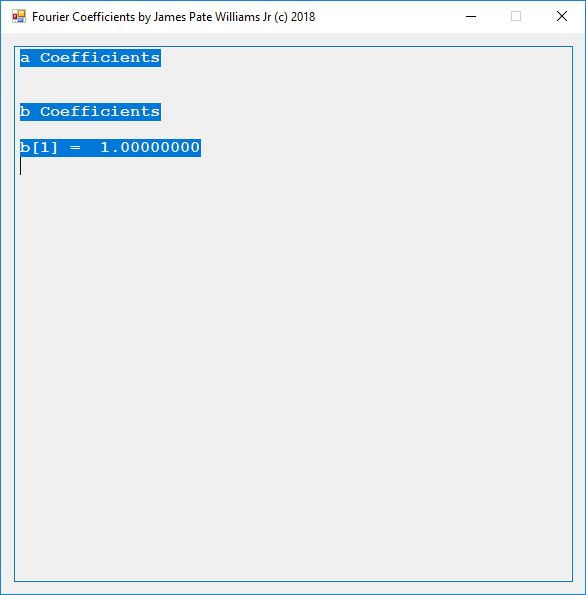
Computerized solutions to Exercises 27.3 to 27.6:


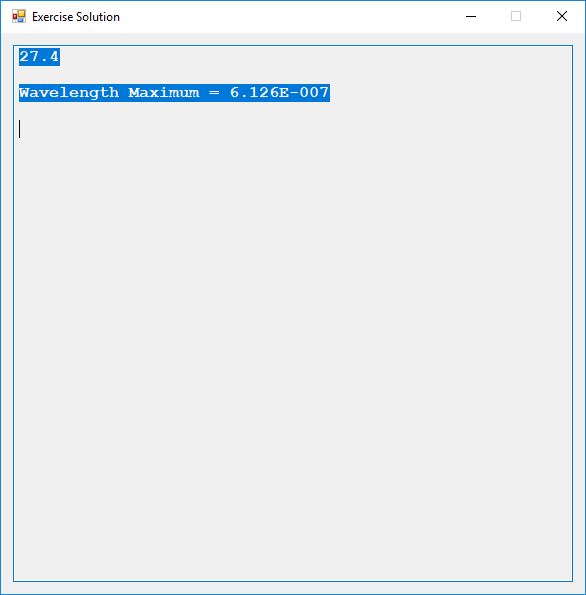
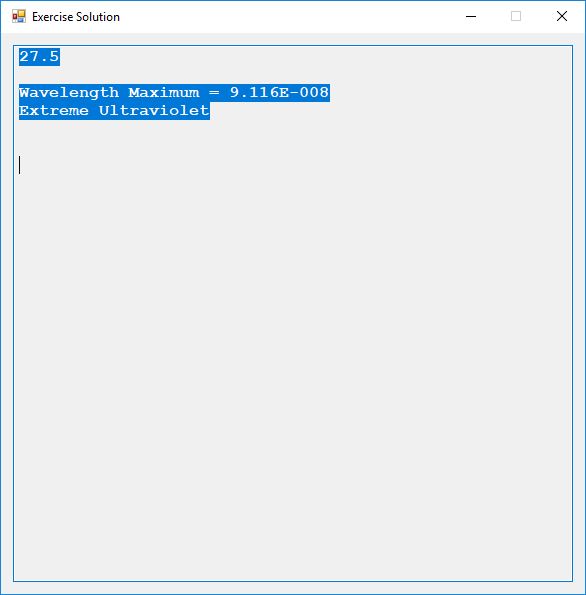
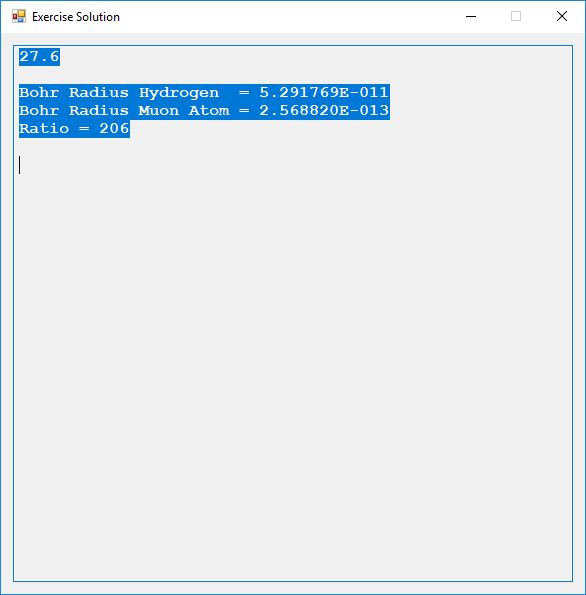
Partial source code for the preceding C# application:
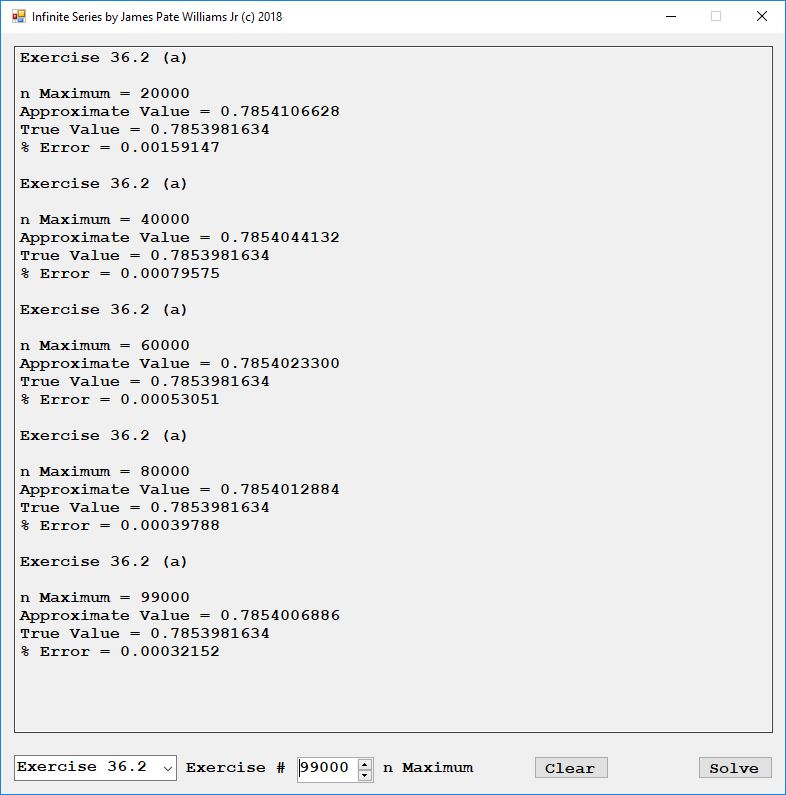
Detailed solutions to Exercises 27.3 to 27.7 in a Portable Document File (PDF):
Exercises 4.1 to 4.7:
Computer solution output of Exercise 4.6:

C# source code for the computer solution of Exercise 4.6, sorry about the naming confusion in the file:
Computer solution of Exercise 4.7 using a velocity square drag function (velocity retardation function is the term used in exterior ballistics). I wrote a baseball ballistics program based on my numeric work (Runge-Kutta Fifth Order) and analytic solutions found in the paper:
Click to access 04-LAJPE-782_Chudinov.pdf
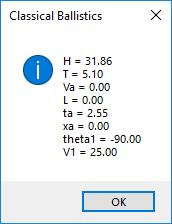
The first picture is the main form interface for the program with the parameters initial velocity in meters per second and the initial angle which is in degrees. We use a velocity of 25 meters per second which is approximately 56 miles per hour and the angle is 90 degrees to the horizontal which is throwing the ball straight up into the air.

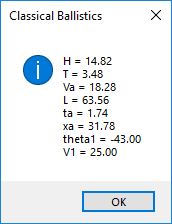
First we show the classical ballistics without atmospheric drag:
Next we show the invalid (due to a singularity in one of the equations) analytic and numeric solutions:

The analytic solution is not valid for theta0 = 90 degrees. The numeric solution shows a time to apogee of 2.28 seconds and time of flight 4.66 seconds. The difference is 4.66 – 2.28 seconds = 2.38 seconds so the time to return from apogee is greater than the time to reach apogee. The analytic solution becomes valid at 88 degrees of inclination.
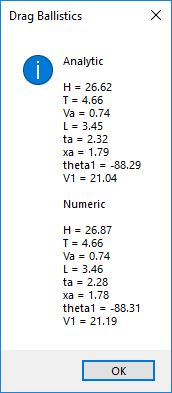
Next we move onto an inclination of 15 degrees:

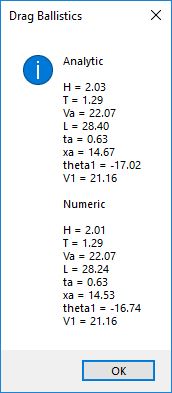
Finally for the maximum distance traveled by the ball classically we select 45 degrees:

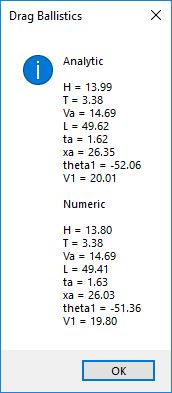
We find that with drag the maximum distance traveled (range) is achieved around 43 degrees: